第1章 二次根式单元测试卷（含解析）

中小学教育资源及组卷应用平台
八年级数学下册
二次根式
单元测试卷
（满分100分）
题号
一
二
三
四
总分
得分
一、选择题（本大题共10小题，共30.0分）
下列判断正确的是（
）
A.
带根号的式子一定是二次根式
B.
一定是二次根式
C.
一定是二次根式
D.
二次根式的值必定是无理数
要使式子有意义，则x的取值范围是(
)
A.
B.
x>-2
C.
x<-2
D.
下列计算正确的是（
）
A.
3×4＝12
B.
＝－3
C.
(－)×＝4－9
D.
(4－3)÷2＝2－
实数a，b，c在数轴上的位置如图，则可以化简为
A.
B.
C.
D.
若x＜y，且(a-3)x＞(a-3)y，则当a为范围内的最大整数时，代数式的值为（???
）
A.
B.
C.
D.
代数式的值为常数2，则a的取值范围是（
）
A.
B.
C.
D.
或
将根号外的因式移到根号内为（???
）
A.
B.
C.
D.
化简（﹣2）2008×（2+）2009的结果是（
）
A.
﹣1
B.
﹣2
C.
+2
D.
﹣﹣2
若，为实数，且，则关于直线，下列说法正确的是（?
??）
A.
直线与轴交点的坐标是（0，3）
B.
直线经过第一、三、四象限
C.
随的增大而减小
D.
与坐标轴围成的三角形面积为
设x、y、z是两两不等的实数，且满足下列等式：，则x3+y3+z3-3xyz的值是（　　）
A.
0
B.
1
C.
3
D.
条件不足，无法计算
二、填空题（本大题共8小题，共24.0分）
若最简二次根式m满足m＋＝0，，则ma＝?
?
?
?
?。
若=a,=
b,
则的值用a,
b可以表示为?
?
?
??。
若0＜a＜1，则﹣的值为?
?
?
?
?
?。
若用a表示的整数部分，用b表示其小数部分，则=______。
若|1
001－a|＋＝a，则a－1
0012＝??????????．
已知x+y=-5，xy=4，则+=______．
若，则m=______，n=______．
设=1++,=1++,=1++,,=1++,
其中n为正整数,则++++的值是?
?
?
?
?。
三、计算题（本大题共1小题，共6.0分）
解答下列各题：
（1）计算：．
（2）已知，，求的值．
四、解答题（本大题共5小题，共40.0分）
如图正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点称为格点，利用正方形网格可以画出长度为无理数的线段，如图1，AB==，请参考此方法按下列要求作图.
（1）在图1中以格点为顶点画一个面积为13的正方形ABCD，并标出字母；
（2）在图2中以格点为顶点画一个△EFM，使EF=2，FM=2，EM=2；
（3）猜想△EFM是什么形状的三角形？并说明理由.
某种牙膏上部圆的直径为2.6cm，下部底边长为4cm，如图，现要制作长方体的牙膏盒，牙膏盒底面是正方形，手工课上小明、小亮、小丽、小芳制作的牙膏盒的高度都一样，且高度符合要求.不同的是底面正方形的边长，他们制作的边长如下表：
制作者
小明
小亮
小丽
小芳
正方形的边长
2cm
2.6cm
3cm
3.4cm
（1）这4位同学制作的盒子都能装下这种牙膏吗？（≈1.42）
（2）若你是牙膏厂的厂长，从节约材料又方便取放牙膏的角度来看，你认为谁的制作更合理？并说明理由.
设，，
(1)当有意义时，求的取值范围；
(2)若为的三边长，求的值.
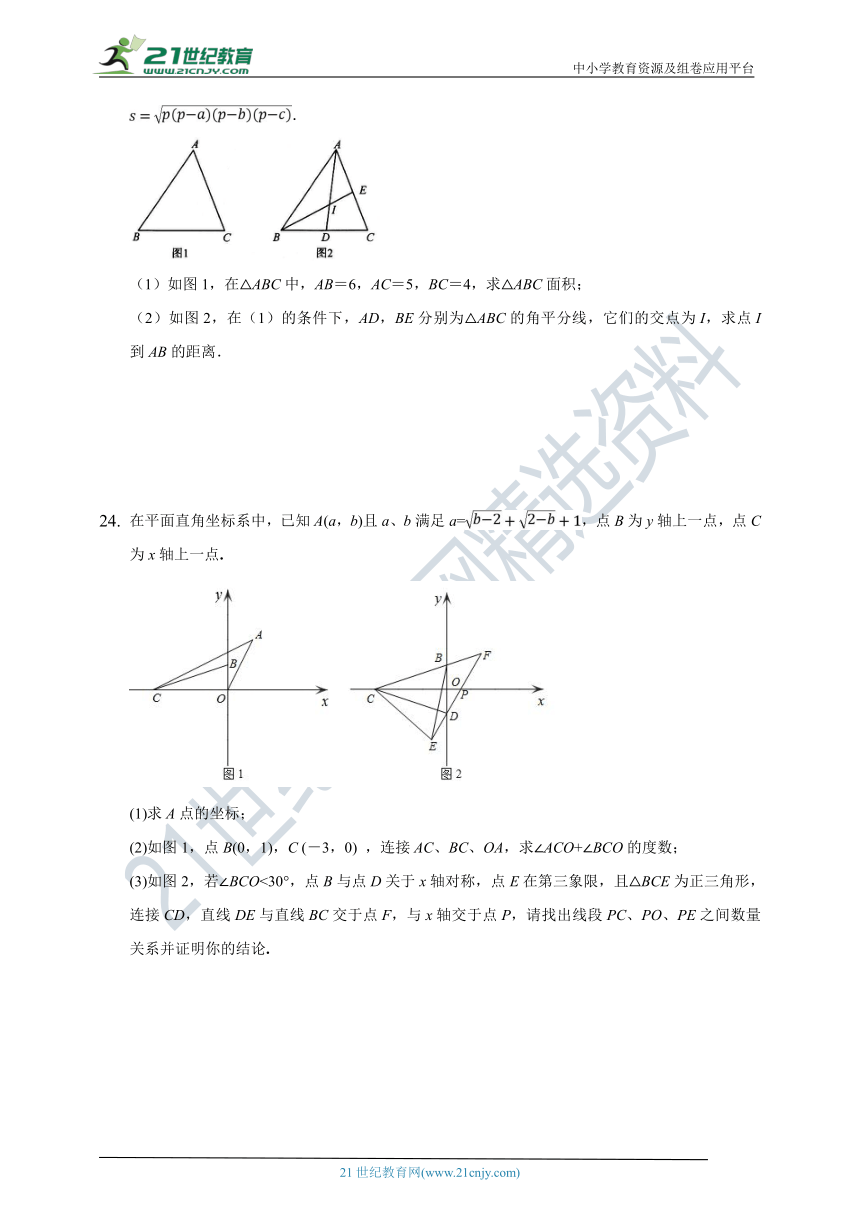
阅读：若一个三角形的三边长分别为a，b，c，设，则这个三角形的面积为．
（1）如图1，在△ABC中，AB＝6，AC＝5，BC＝4，求△ABC面积；
（2）如图2，在（1）的条件下，AD，BE分别为△ABC的角平分线，它们的交点为I，求点I到AB的距离．
在平面直角坐标系中，已知A(a，b)且a、b满足a=，点B为y轴上一点，点C为x轴上一点.
(1)求A点的坐标；
(2)如图1，点B(0，1)，C
(－3，0)
，连接AC、BC、OA，求∠ACO+∠BCO的度数；
(3)如图2，若∠BCO<30°，点B与点D关于x轴对称，点E在第三象限，且△BCE为正三角形，连接CD，直线DE与直线BC交于点F，与x轴交于点P，请找出线段PC、PO、PE之间数量关系并证明你的结论.
答案和解析
1.【答案】B
【解析】解：A、带根号的式子不一定是二次根式，故此选项错误；
B、一定是二次根式，故此选项正确；
C、?，a≥1时，一定是二次根式，故此选项错误；
D、二次根式的值不一定是无理数，故此选项错误；
2.【答案】B
【解析】解：依题意得：x+2＞0，
解得x＞-2.
3.【答案】D
【解析】解：A.原式=24，所以A选项的计算错误；
B.原式=3，所以B选项的计算错误；
C.原式=，所以C选项的计算错误；
D.原式=2－，所以D选项的计算正确．
4.【答案】D
【解析】解：由数轴可得出：a＜0，a-b＞0，c-a＜0，
∴原式=-a-(a-b)-(c-a)，
=-a-a+b-c+a，
=-a+b-c.
5.【答案】A
【解析】本题主要考查了不等式的性质和二次根式的化简求值，解答此题的关键是由不等式的性质得到a的取值范围.
解：∵x＜y，且(a-3)x＞(a-3)y，
∴a-3<0，∴a<3，
又∵a为范围内的最大整数，
∴a的值为2，
当a=2时，=.
6.【答案】C
【解析】本题考查了二次根式的性质，分类讨论是解题关键．根据=2，可分类讨论，根据二次根式的性质，可得答案．
解：由题意得=2，
当a≤1时，原式=1-a+3-a=4-2a≠2
当1≤a≤3时，原式=a-1+3-a=2，
当a≥3时，原式=a-1+a-3≠2，
故选C．
7.【答案】B
【解析】解：由题意可知a＜0，
∴a=-=-．
直接利用二次根式的性质得出a的符号，进而变形得出答案．
8.【答案】C
【解析】解：原式=[（-2）（+2）]2008?（+2）
=（3-4）2008?（+2）
=+2．
9.【答案】B
【解析】本题主要考查了二次根式的非负性的应用和一次函数的图象与性质，解答此题可先根据二次根式的非负性得到a的值，然后求出b的值，从而可得一次函数的解析式，再结合一次函数的图象和性质解答即可.
解：∵，
∴,
解得：a=，
∴b=-3，
∴一次函数的解析式为：y=.
∴A.当x=0时，y=-3，故直线与y轴的交点坐标为（0，-3），故该选项错误；
B.直线经过一，三，四象限，故该选项正确；
C.∵k=>0，故y随x的增大而增大，故该选项错误；
D.令y=0，可得x=,令x=0，可得y=-3，
∴直线与坐标轴围成的三角形的面积为：，故该选项错误.
10.【答案】A
【解析】解：依题意得：
，
解得x=0，
∵，
∴，
∴y=-z
∴把x=0，y=-z代入x3+y3+z3-3xyz得：原式=（-z）3+z3=0
由二次根式有意义可知x-z≥0，x3（y-x）3≥0，x3（z-x）3≥0，可得x=0，y=-z．代入代数式即可求解．
11.【答案】－1
【解析】解：最简二次根式m满足m＋＝0，
∴m=-1，2a+1=7，
∴a=3，
∴
12.【答案】???????
【解析】?解：∵，，
∴．
13.【答案】﹣2a
【解析】解：原式=
=
=-
=，
∵0＜a＜1，
∴a+＞0，
a-=＜0，
∴原式=-(a-)-（a+）
=-a+-a-
=-2a
14.【答案】
【解析】解：=+1，
∵1<<2，
∴2<+1<3，
∵用a表示的整数部分，用b表示其小数部分，
∴a=2，b=+1-2=-1，
∴原式=×2-（-1）2
=2-2-1+2
=4-3.
15.【答案】1002
【解析】解：根据算术平方根的非负性，
a-10020，解得a1002，
|1
001－a|＋
=a-1001+=a，即=1001，
解得a=+1002，
a-=+1002-=1002.
16.【答案】
【解析】解：∵x+y=-5，xy=4，
∴x＜0，y＜0，
+=-（+）=-，
∵x+y=-5，xy=4，
∴原式=-=-=．
先化简+，再代入求值即可．
17.【答案】3?
2
【解析】解：∵＞，即-＞0，
∴=
=
=
=|-|
=-，
又∵=-，
则m=3，n=2．
此题考查了二次根式的化简求值，其技巧性较强，灵活变换等式左边的被开方数是解本题的关键．
18.【答案】2020???????
【解析】解：∵n为正整数，
∴=
=
=
=
=
=1+，
∴=（1+）+（1+）+（1+）+…+（1+）
=2020+1-+
=2020+1-
=2020．
计算通项公式，将n=1，2，3，…，2020代入可得结论．
本题考查了二次根式的化简求值，解题的关键是用裂项法将分数代成，再化简，寻找抵消规律求和．
19.【答案】解：（1）原式＝0；
（2）解：∵，，
∴，
=，
=18，
∴
20.【答案】解：（1）如图1所示，四边形ABCD即为所求作的正方形；
（2）如图2所示，△EFM即为所求作三角形（答案不唯一）；
（3）△EFM为等腰直角三角形，
∵EF2+FM2=（2）2+（2）2=40，
EM2=（2）2=40，
∴EF2+FM2=EM2，即△EFM为直角三角形，
又∵EF=FM=2，∴△EFM为等腰直角三角形．
21.【答案】（1）牙膏恰好放入牙膏盒内，牙膏下底部长与牙膏盒底面对角线长相等．
设底面正方形的边长为a，则根据勾股定理得：
2a2=42，解得??a=±（±2），
因为a不能为负，所以a为=（2）；
因此，只要牙膏盒底面边长大于或等于2.84cm，牙膏盒都能装下这种牙膏，
所以小丽和小芳制作的盒子能装下这种牙膏．
（2）小丽制作的牙膏盒更合理．因为她制作的盒子既节约材料又方便取放牙膏．
22.【答案】解：（1）∵a有意义，
∴8-x≥0，∴x≤8；
（2）方法一：分三种情况：
①当a2+b2=c2，即8-x+4=6，得x=6，
②当a2+c2=b2，即8-x+6=4，得x=10，
③当b2+c2=a2，即4+6=8-x，得x=-2，
又∵x≤8，∴x=6或-2；
方法二：∵直角三角形中斜边为最长的边，c＞b
∴存在两种情况，
①当a2+b2=c2，即8-x+4=6，得x=6，
②当b2+c2=a2，即4+6=8-x，得x=-2，
∴x=6或-2．
【解析】此题主要考查了二次根式的应用以及勾股定理等知识，利用分类讨论得出是解题关键．
23.【答案】解：（1）由题意，得：a=4，b=5，c=6；
∴p==；
∴S===，
故△ABC的面积是；
（2）如图，过点I作IF⊥AB、IG⊥AC、IH⊥BC，垂足分别为点F、G、H，
∵AD、BE分别为△ABC的角平分线，
∴IF=IH=IG，
∵S△ABC=S△ABI+S△ACI+S△BCI，
即=×6?IF+×5?IG+×4?IH，
∴3?IF+?IF+2?IF=，
解得IF=，
故I到AB的距离为．
【解析】本题主要考查三角形面积的计算和角平分线的性质，熟练掌握角平分线的性质是解题的关键．
（1）先根据三边长度求出p的值，再代入公式计算可得；
（2）过点I作IF⊥AB、IG⊥AC、IH⊥BC，由角平分线性质可得IF=IH=IG，再根据S△ABC=S△ABI+S△ACI+S△BCI即可求得IF的长．
24.【答案】解：（1）∵a、b满足a=,
∴b=2，a=1，
A（1，2）；
（2）如图，作B点关于x轴的对称点D，连接CD、AD，
∵点B（0，1），C
(－3，0），A（1，2），
∴D（0，-1），
AD2=12+32=10，CD2=12+32=10，AC2=（1+3）2+22=20，
∴AC2=AD2+CD2，
∴△ADC为等腰直角三角形，且∠ADC=90°，
∴∠ACD=45°，
∵B、D关于x轴对称，
∴∠BCO=∠DCO，
∴∠ACO+∠BCO=∠ACO+∠DCO=∠ACD=45°；
（3）线段PC、PO、PE之间数量关系是PC=PE+2PO.
∵点B与点D关于x轴对称，
∴CD=BC，∠2=∠4，
∵△BCE为正三角形，
∴BC=CE=EB，∠BCE=∠CEB=60°，
∴CD=CE，
∴∠CED=∠CDE，
∴∠2=（60°-∠3）=30°-∠3，∠CED=（180°-∠3）=90°-∠3，
∴∠1=∠CED-∠CEB=（90°-∠3）-60°=30°-∠3，
∴∠1=∠2，
在CP截取CH=EP，在△CBH和△EBP中，
,
∴△CBH≌△EBP，
∴BH=BP，
∴HO=OP，
∴PC=CH+HP=PE+2PO，
即PC=PE+2PO.
【解析】此题主要考查坐标与图形的性质，全等三角形的判定与性质，轴对称的性质，等边三角形的判定与性质，等腰直角三角形的判定与性质，勾股定理逆定理，三角形内角和定理，等腰三角形的性质，二次根式的意义.此题综合性比较强，难度较大.
（1）根据二次根式的意义求出b和a的值，即可得到A点的坐标；
（2）作B点关于x轴的对称点D，连接CD、AD，证明△ADC为等腰直角三角形，且∠ADC=90°，得到∠ACD=45°，再根据B、D关于x轴对称，即可求∠ACO+∠BCO的度数；
（3）根据点B与点D关于x轴对称，△BCE为正三角形，利用三角形内角和定理证明∠1=∠2，在CP截取CH=EP，证明△CBH≌△EBP，得到BH=BP，再根据等腰三角形三线合一的性质可得HO=PO，即可得到线段PC、PO、PE之间数量关系.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)