二次函数复习

(共12张PPT)
二次函数复习之数形结合
如图，抛物线y=ax2+bx+c与x轴的一个交点在点（－2，0）和（－1，0）之间，
y
x
O
－2
1
－1
练习1：
（1）求当y=0时，方程ax2+bx+c=0的两根的取值范围。
（2）若顶点坐标为（1，2.5）,
根据图象求方程ax2+bx+c－2=0的根的情况。
请归纳方程ax2+bx+c=k的根的情况。
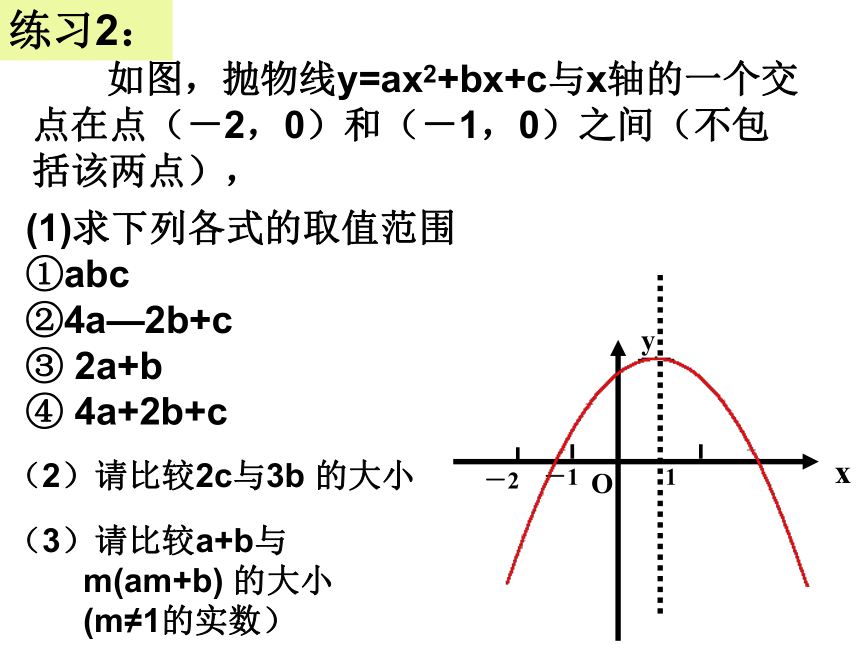
如图，抛物线y=ax2+bx+c与x轴的一个交点在点（－2，0）和（－1，0）之间（不包括该两点），
练习2：
y
x
O
－2
1
－1
(1)求下列各式的取值范围
①abc
②4a—2b+c
③ 2a+b
④ 4a+2b+c
（3）请比较a+b与
m(am+b) 的大小
(m≠1的实数）
（2）请比较2c与3b 的大小
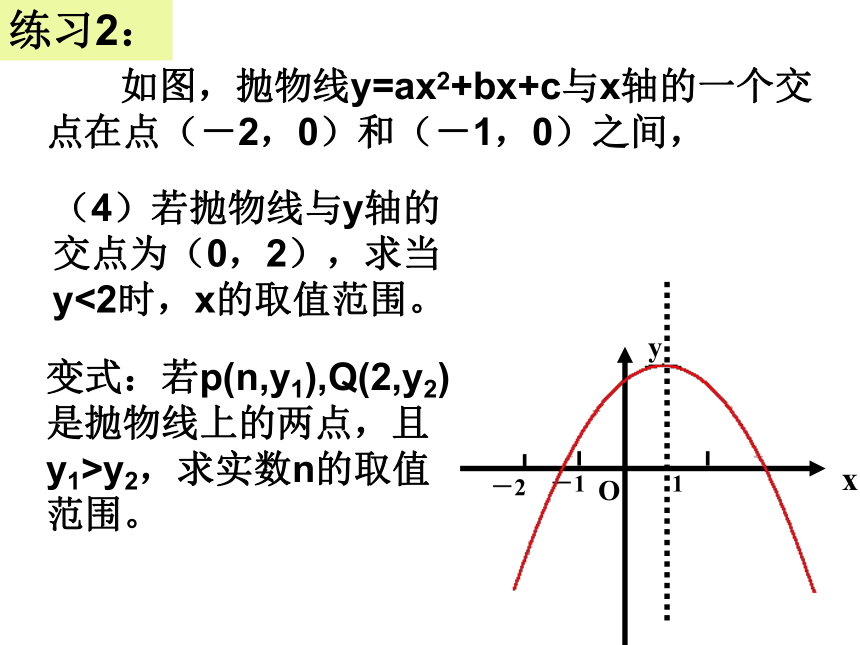
如图，抛物线y=ax2+bx+c与x轴的一个交点在点（－2，0）和（－1，0）之间，
y
x
O
－2
1
－1
练习2：
（4）若抛物线与y轴的交点为（0，2），求当y<2时，x的取值范围。
变式：若p(n,y1),Q(2,y2)是抛物线上的两点，且y1>y2，求实数n的取值范围。
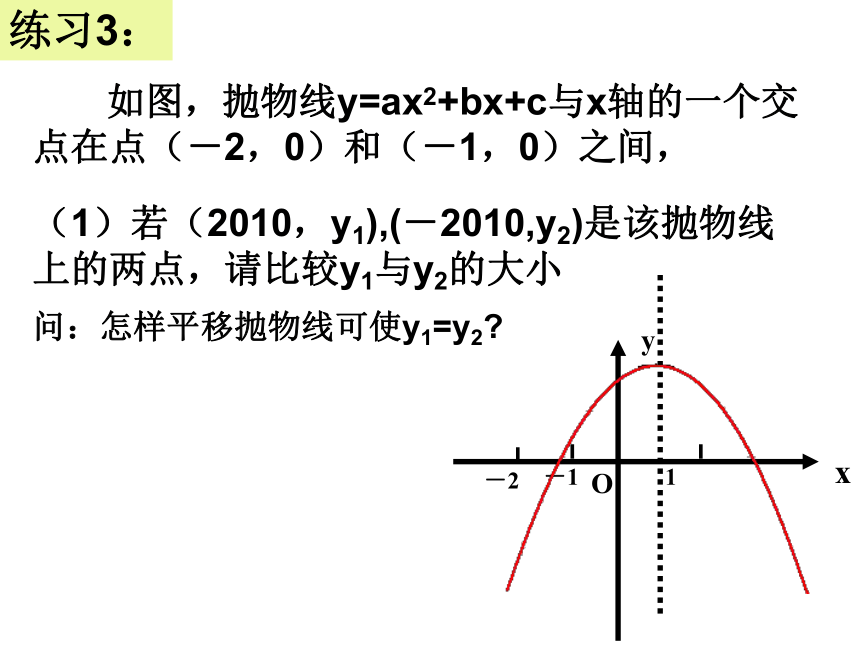
如图，抛物线y=ax2+bx+c与x轴的一个交点在点（－2，0）和（－1，0）之间，
（1）若（2010，y1),(－2010,y2)是该抛物线上的两点，请比较y1与y2的大小
练习3：
问：怎样平移抛物线可使y1=y2
y
x
O
－2
1
－1
思考：观察结果，当 自变量取 时，函数值与原解析式哪个系数有关？如何解释？
练习3：
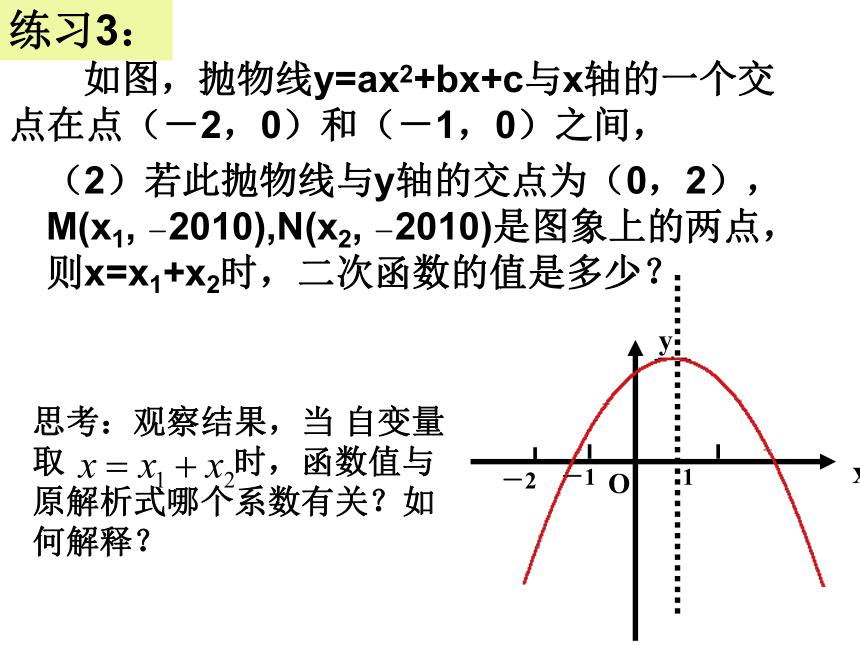
（2）若此抛物线与y轴的交点为（0，2），M(x1, －2010),N(x2, －2010)是图象上的两点，则x=x1+x2时，二次函数的值是多少？
如图，抛物线y=ax2+bx+c与x轴的一个交点在点（－2，0）和（－1，0）之间，
y
x
O
－2
1
－1
练习4：
如图，抛物线y=ax2+bx+c与x轴的一个交点在点（－2，0）和（－1，0）之间，
y
x
O
－2
1
－1
问当x>2时，y随 x 的变化情况。
若抛物线y=mx2+(2m—1)x+1(m≠0),对任意正实数m,当x<—2时，问y随x的变化情况。
提升训练：
变式1：
如图，抛物线y=ax2+bx+c与x轴的一个交点A在点（－2，0）和（－1，0）之间(包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，求a的取值范围。
变式2：
如图，四边形ABCD为正方形，A(1，1)，B（2，1），抛物线y=ax2(a>0)若要与正方形有交点，求a的取值范围。
y
x
O
x
A
B
1
2
1
如图，点A，B的坐标分别为（1, 4）和（4, 4）,抛物线 的顶点在线段AB上运动，与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为—3，则点D的横坐标最大值为( )
A．－3 　 B．1 C．5 D．8
y
x
O
（第10题）
变式1：
如图，两条抛物线 、 与分别经过点(—2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为
Ａ．8　 Ｂ．6　 Ｃ．10　 Ｄ．4　
、
(9题图)
练习2：
变式2：
A
B
Q
O
x
y
如图，二次函数y=ax2+bx+c的图象如图所示，Q(n,3)是图象上一点，且AQ⊥BQ,则a的值是多少。