二次函数图象复习

(共28张PPT)
看图说话：
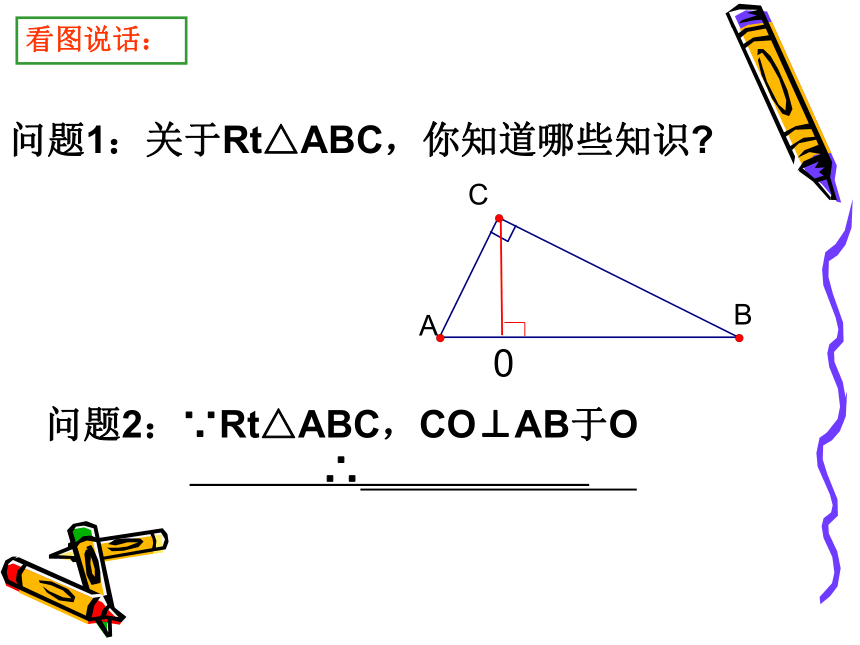
问题1：关于Rt△ABC，你知道哪些知识
0
问题2：∵Rt△ABC，CO⊥AB于O
∴
看图说话3：
0
x
y
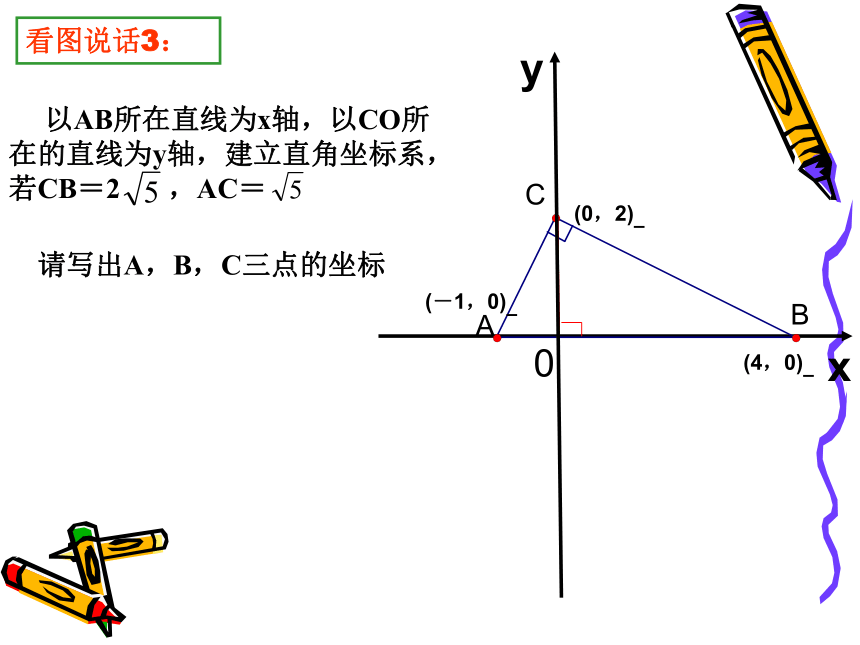
以AB所在直线为x轴，以CO所在的直线为y轴，建立直角坐标系，若CB＝2
，AC＝
请写出A，B，C三点的坐标
(－1，0)
(4，0)
(0，2)
看图说话4：
0
x
y
(－1，0)
(4，0)
(0，2)
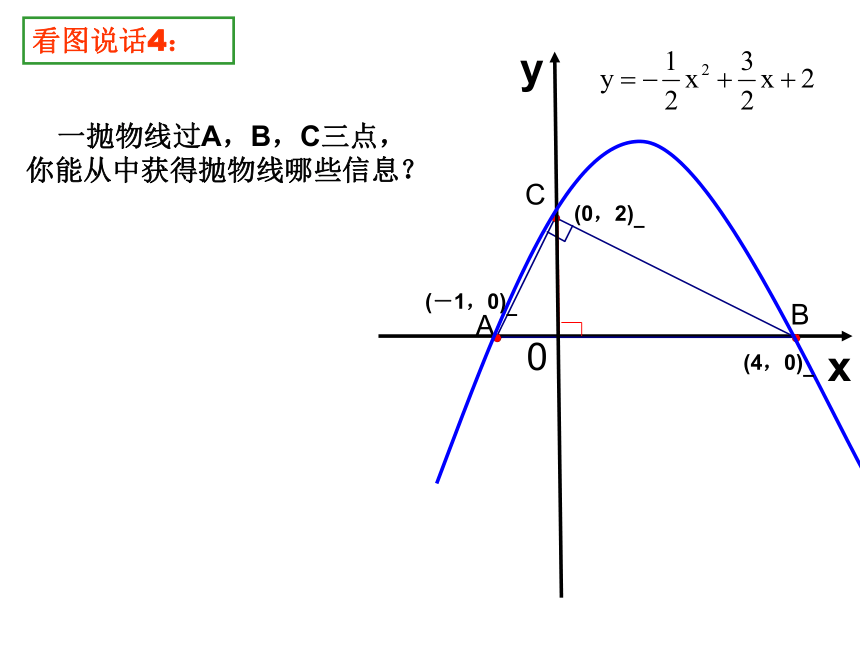
一抛物线过A，B，C三点，
你能从中获得抛物线哪些信息？
看图说话5：
0
x
y
(－1，0)
(4，0)
(0，2)
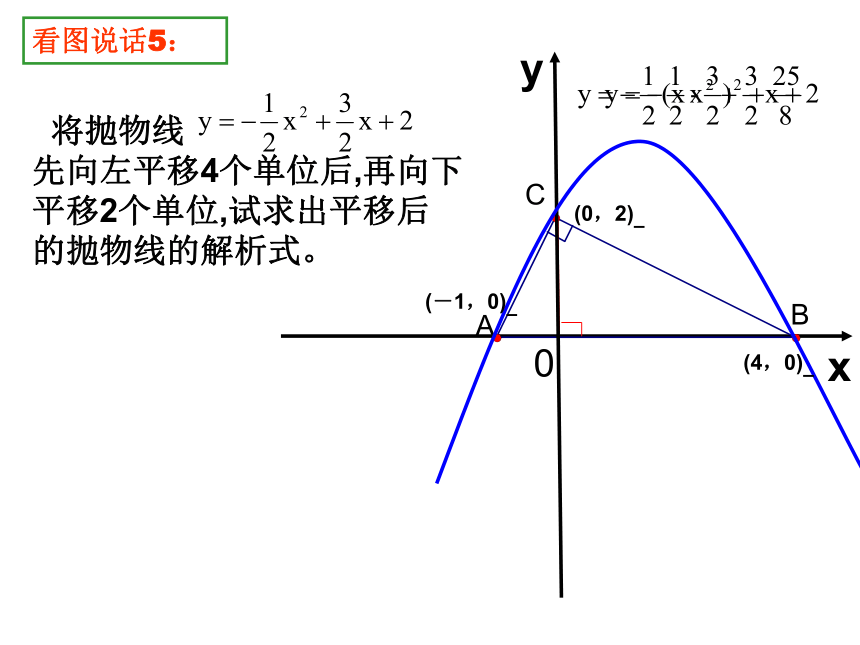
将抛物线 先向左平移4个单位后,再向下平移2个单位,试求出平移后
的抛物线的解析式。
看图说话6：
0
x
y
(－1，0)
(4，0)
(0，2)
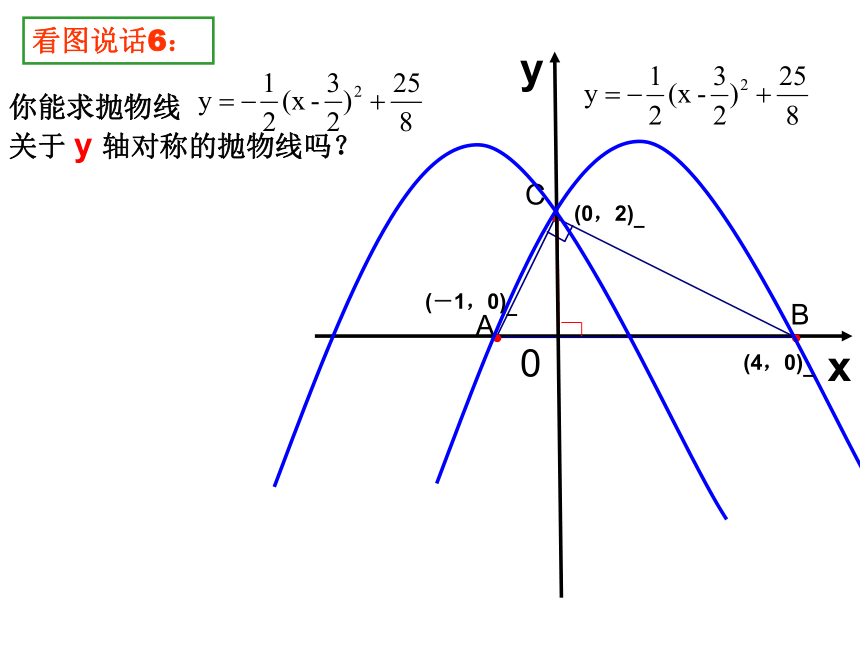
你能求抛物线
关于 y 轴对称的抛物线吗？
看图说话6：
0
x
y
(－1，0)
(4，0)
(0，2)
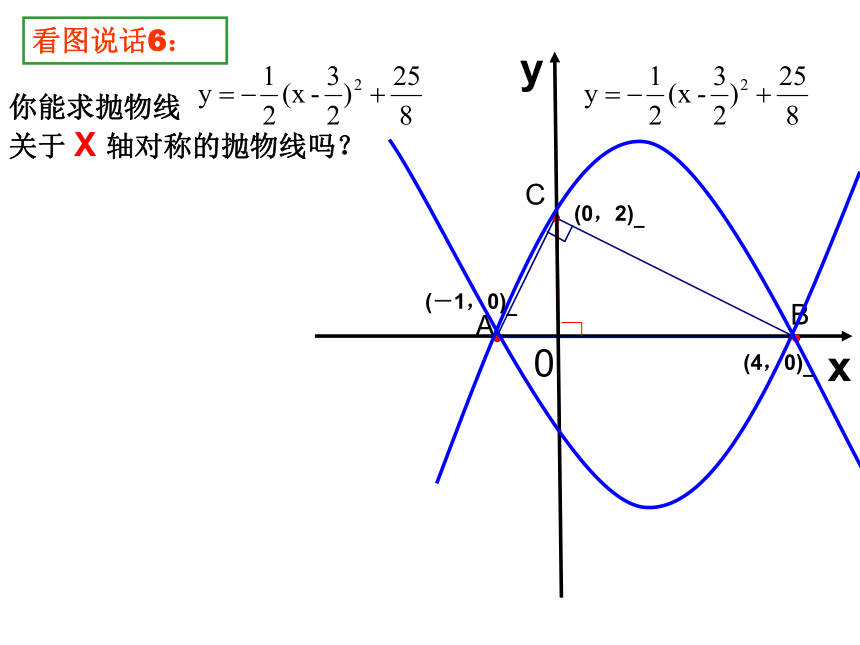
你能求抛物线
关于 X 轴对称的抛物线吗？
0
x
y
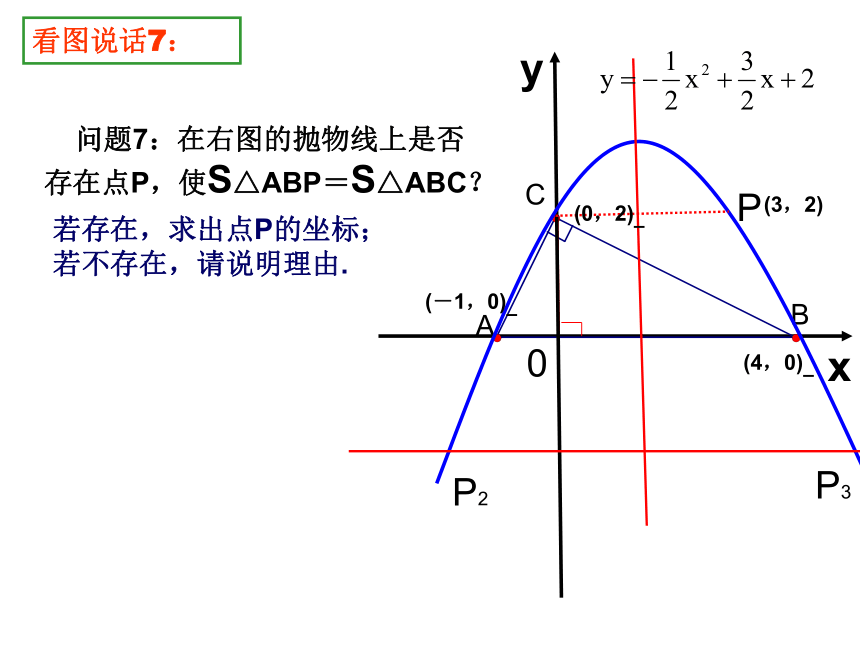
问题7：在右图的抛物线上是否
存在点P，使S△ABP＝S△ABC？
若存在，求出点P的坐标；
若不存在，请说明理由.
P
(－1，0)
(0，2)
(4，0)
P3
P2
看图说话7：
(3，2)
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话7：
D
(3，2)
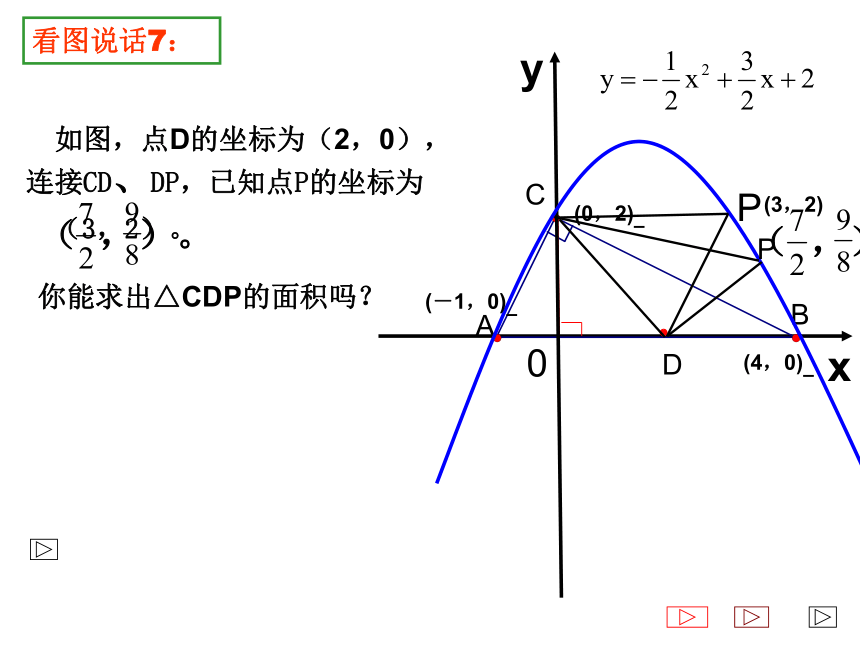
如图，点D的坐标为（2，0），
连接CD、DP，已知点P的坐标为
你能求出△CDP的面积吗？
P
（ ，）。
（ ，）。
（3，2）。
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话7：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P的坐标为
你能求出△CDP的面积吗？
（ ，）。
F
（ ，）。
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话7：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P的坐标为
你能求出△CDP的面积吗？
（ ，）。
（ ，）。
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话7：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P的坐标为
你能求出△CDP的面积吗？
（ ，）。
（ ，）。
M
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话7：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P（x1，y1）是该抛物线上的一个动点（其中x1>0，y1>0），
请问：△CDP是否有最大面积？
若有，求出△CDP的最大面的
最大面积和此时点P的坐标；
若没有，请说明理由。
F
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话8：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P （x1，y1） 是该抛物线上的一个动点（其中x1>0，y1>0 ），
E
请问：当△BDE是等腰三角形
时，请直接写出此时点E的坐标。
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话8：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P （x1，y1） 是该抛物线上的一个动点（其中x1>0，y1>0 ），
E
请问：当△BDE是等腰三角形时，
你能直接写出此时点E的坐标。
① DE=BE 时
F
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话8：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P （x1，y1） 是该抛物线上的一个动点（其中x1>0，y1>0 ），
E
请问：当△BDE是等腰三角形时，
你能直接写出此时点E的坐标。
② DB=BE 时
F
0
x
y
P
(－1，0)
(0，2)
(4，0)
看图说话8：
D
如图，点D的坐标为（2，0），
连接CD、DP，已知点P （x1，y1） 是该抛物线上的一个动点（其中x1>0，y1>0 ），
E
请问：当△BDE是等腰三角形时，
你能直接写出此时点E的坐标。
③ DB=DE 时
F
二次函数的小结
通过本节课的学习，谈谈你的收获和
体会与大家一起分享好吗？
例1、 如图，已知直线 y= -x+3与X轴、y轴分别交于点B、C，抛物线y= -x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（1）求抛物线的解析式；
解：令y=0，则 –x+3=0，x=3，
∴B（3，0），
令x=0， 则y=3，
∴C（0，3），
b=2
c=3
｛
解得
-9+3b+c=0
c=3
｛
得
∴ y= -x2+2x+3
（3，0）
（0，3）
x
y
o
A
B
C
例1、如图，已知直线 y= -x+3与X轴、y轴分别交于点B、C，抛物线y= -x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（1）求抛物线的解析式；
（2）若抛物线的顶点为D，求三角形BDC的面积；
（3，0）
（0，3）
B
C
D
x
y
o
A
E
（1，4）
（1，0）
（-1，0）
例1、 如图，已知直线 y= -x+3与X轴、y轴分别交于点B、C，抛物线y= -x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（3）在直线y= -x+3上是否存在点P，使S△PAC= 1/2 S △PAB ？若存在，求出点P的坐标；若不存在，说明理由；
（3，0）
（0，3）
x
y
o
A
B
C
y
（3，0）
（0，3）
x
o
A
B
C
P
Q
P
（3，0）
（0，3）
x
y
o
A
B
C
Q
例3、如图，已知直线 y= -x+3与X轴、y轴分别交于点B、C，抛物线y= -x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（1）求抛物线的解析式；
（2）若抛物线的顶点为D，求三角形BDC的面积； （3）在直线y= -x+3上是否存在点P，使S△PAC= 1/2 S △PAB ？若存在，求出点P的坐标；若不存在，说明理由; （4）抛物线上是否存在点P，使三角形PCB的面积等于三角形DCB的面积？如存在，求出所有符合条件的坐标；若不存在，请说明理由
（3，0）
（0，3）
B
C
D
x
y
o
A
E
（1，4）
（1，0）
（-1，0）
已知二次函数
的图象如图所示.
用一用
1.则关于x的一元二次方程
的解为 ．
X1=-1,x2=5
x
y
O
（5，0）
知识小结
二次函数解析式的求法；
利用抛物线的轴对称性解决相应问题；
（1）找对称点
（2）求相关的方程的解
（3）比较函数值的大小
二次函数图象
开口方向
对称轴
顶点坐标
增减性
图象平移