第2章 一元二次方程单元测试卷(含解析)
文档属性
| 名称 | 第2章 一元二次方程单元测试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 460.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学下册
一元二次方程
单元测试卷
(满分100分)
题号
一
二
三
四
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列方程为一元二次方程的是( )
A.
x2-3=x(x+4)
B.
x2-=3
C.
x2-10x=-5
D.
4x+6xy=33
方程x2=-x的解是(???
)
A.
1
B.
-1
C.
1或0
D.
-1或0
一元二次方程kx2-2x-2=0有实数根,则k的取值范围是( )
A.
k≥-且k≠0
B.
k≥-1
C.
k≤-1且k≠0
D.
k≥-1或k≠0
关于x的方程x2+5x+m=0的一个根为﹣2,则另一个根是(
)
A.
﹣6
B.
﹣3
C.
3
D.
6
等腰三角形的三边均满足方程x2-7x+10=0,该等腰三角形的周长是( )
A.
12
B.
12或9
C.
12或6或15
D.
12或9或6或15
在一次数学兴趣小组活动中,每两名学生握手一次,但小明因中途有事离开,他记得有3人没有和他握过手,经统计所有握手共42次.若设参加活动的学生为x名,据题意可列方程为( )
A.
x(x-1)-3=42
B.
C.
D.
已知(x2+y2+2)(x2+y2+4)=15,则x2+y2的值为( )
A.
-7或1
B.
1
C.
-7
D.
7或-1
一面足够长的墙,用总长为30米的木栅栏图中的虚线围一个矩形场地ABCD,中间用栅栏隔成同样三块,若要围成的矩形面积为54平方米,设垂直于墙的边长为x米,则x的值为(
)
3
B.
4
C.
3或5
D.
3或
若是方程+2x+c=0(a0)的一个根,设M=1-ac,N=,则M与N的大小关系为(
)
A.
M>N
B.
M=N
C.
M
D.
无法确定
定义[x]表示不超过实数x的最大整数,如[1.8]=1、[-1.4]=-2、[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=在-2≤x<2时的解为(?
?
?
)
???????
A.
0或
B.
0或2
C.
1或-
D.
或-
二、填空题(本大题共8小题,共24.0分)
关于x的方程(k+1)x|k-1|+kx+1=0是一元二次方程,则k的值为______
.
已知a是方程x2-3x-1=0的一个根,则代数式-2a2+6a-3的值是______
.
已知方程x2+5x-6=0的解是x1=1,x2=-6,则方程(2x+3)2+5(2x+3)-6=0的解是______
.
已知非零有理数x、y满足x2-4xy+3y2=0,则=______.
如图,在一个长20m,宽10m的矩形草地内修建宽度相等的小路(阴影部分),若剩余草地(空白部分)的面积171m2,则小路的宽度为______m.
如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的有 个.
①方程x2-x-2=0是倍根方程;
②若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
③若p、q满足pq=2,则关于x的方程px2+3x+q=0是倍根方程;
④若方程ax2+bx+c=0是倍根方程,则必有2b2=9ac.
关于x的一元二次方程x2+2(m-1)x+m2=0的两个实数根分别为x1,x2,且x1+x2>0,x1x2>0,则m的取值范围是?
?
?
?
?。
如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为____________________.
三、计算题(本大题共1小题,共6.0分)
用适当的方法解下列方程
(1)(2x+1)2=3(2x+1)
(2)3x2-3x-1=0.
四、解答题(本大题共5小题,共40.0分)
已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
如图是一张长24
cm,宽12
cm的矩形铁皮,将其剪去一个小正方形和两个矩形,剩余部分(阴影部分)恰好可制成一个有盖的长方体铁盒.
(1)a=________;
(2)若铁盒底面积是80
cm2,求剪去的小正方形边长.
随着全球疫情的爆发,医疗物资的极度匮乏,中国许多企业都积极的宣布生产医疗物资以应对疫情,某工厂及时引进了一条口罩生产线生产口罩,开工第一天生产500万个,第三天生产720万个,若每天增长的百分率相同.试回答下列问题:
(1)求每天增长的百分率;
(2)经调查发现,1条生产线最大产能是1500万个/天,若每增加1条生产线,每条生产线的最大产能将减少50万个/天,现该厂要保证每天生产口罩6500万件,在增加产能同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
如图,在△ABC中.∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果点P、Q分别从A、B同时出发,那么几秒后△PBQ的面积等于4cm2?
(2)在(1)中△PBQ的面积能否等于7?请说明理由.
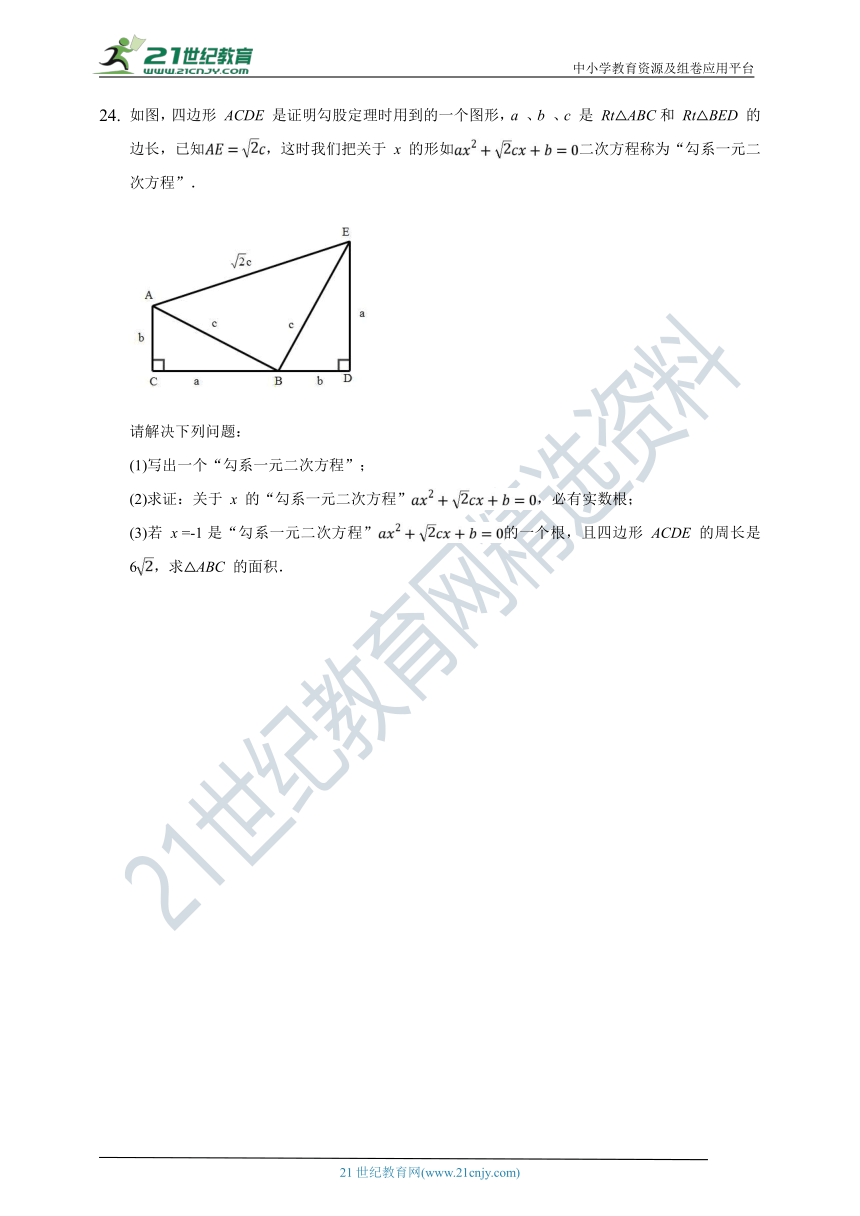
如图,四边形
ACDE
是证明勾股定理时用到的一个图形,a
、b
、c
是
Rt△ABC和
Rt△BED
的边长,已知,这时我们把关于
x
的形如二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于
x
的“勾系一元二次方程”,必有实数根;
(3)若
x
=-1是“勾系一元二次方程”的一个根,且四边形
ACDE
的周长是6,求△ABC
的面积.
答案和解析
1.【答案】C
【解析】解:A、方程化简得:4x+3=0,是一元一次方程,不符合题意;
B、x2-=3为分式方程,不符合题意;
C、x2-10x=-5是一元二次方程,符合题意;
D、4x+6xy=5是二元二次方程,不符合题意.
2.【答案】D
【解析】解:方程
x2=-x,
移项,x2+x=0,
提公因式,x(x+1)=0,
得,x=0,x+1=0,
解得,x1=0,x2=-1
3.【答案】A
【解析】解:∵一元二次方程kx2-2x-2=0有实数根,
∴△=b2-4ac=(-2)2-4k×(-2)=4+8k≥0,k≠0,
解得:k≥-且k≠0
本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.
4.【答案】B
【解析】解:设方程的另一个根为n,
则有-2+n=-5,
解得:n=-3.
本题考查了根与系数的关系,牢记两根之和等于-、两根之积等于是解题的关键.
5.【答案】C
【解析】解:∵x2-7x+10=0,
∴(x-2)(x-5)=0.
∴x-2=0或x-5=0.
解得x=2或x=5.
当等腰三角形的腰长为2,底长为5时,由于2+2<5,构不成三角形;
当等腰三角形的腰长为2,底长为2时,该等腰三角形的周长为2+2+2=6;
当等腰三角形的腰长为5,底长为2时,该等腰三角形的周长为:5+5+2=12;
当等腰三角形的腰长为5,底长为5时,该等腰三角形的周长为:5+5+5=15.
先求解一元二次方程,再根据等腰三角形分类讨论.
6.【答案】C
【解析】解:参加此会的学生为x名,每个学生都要握手(x-1)次,
∴可列方程为x(x-1)-3=42
每个学生都要和他自己以外的学生握手一次,但两个学生之间只握手一次,所以等量关系为:×学生数×(学生数-1)=总握手次数,把相关数值代入即可求解.
7.【答案】B
【解析】解:设t=x2+y2(t≥0),则原方程转化为(t+2)(t+4)=15,
整理,得(t+7)(t-1)=0.
解得t=-7(舍去)或t=1.
所以x2+y2的值为1.
本题主要考查了换元法解一元二次方程,换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理.
8.【答案】D
【解析】解:设垂直于墙的边长为x米,由题意可得,
x(30-4x)=54,整理得:2x2-15x+27=0,
解得:x1=4.5,x2=3,
即x的值为:3或4.5.
9.【答案】B
【解析】把x0代入方程ax2+2x+c=0得ax02+2x0=-c,作差法比较可得.
解:∵x0是方程ax2+2x+c=0(a≠0)的一个根,
∴ax02+2x0+c=0,即ax02+2x0=-c,
则N-M=(ax0+1)2-(1-ac)
=a2x02+2ax0+1-1+ac
=a(ax02+2x0)+ac
=-ac+ac
=0,∴M=N.
10.【答案】A
【解析】本题主要考查的是新定义,函数的图象的有关知识,根据新定义和函数图象讨论;然后分别解关于x的一元二次方程即可.
解:当1x<2时,=1,解得=,=-(舍去);
当0x<1时,=0,解得x=0;
当-1x<0时,=-1,方程没有实数解;
当-2x<-1时,=-2,方程没有实数解;
所以方程[x]=的解为0或
11.【答案】3
【解析】解:由题意得,,
解得k=3.
一元二次方程必须满足两个条件:(1)未知数的最高次数是2;(2)二次项系数不为0.由这两个条件得到相应的关系式,再求解即可.
12.【答案】-5
【解析】解:∵a是方程x2-3x-1=0的一个根,
∴a2-3a-1=0,
整理得,a2-3a=1,
∴-2a2+6a-3=-2(a2-3a)-3
=-2×1-3
=-5
根据方程的根的定义,把x=a代入方程求出a2-3a的值,然后整体代入代数式进行计算即可得解.
13.【答案】x1=-1,x2=-
【解析】解:把方程(2x+3)2+5(2x+3)-6=0看作关于2x+3的一元二次方程,
所以2x+3=1或2x+3=-6,
所以x1=-1,x2=-.
14.【答案】0或
【解析】解:∵非零有理数x、y满足x2-4xy+3y2=0,
∴(x-y)(x-3y)=0,
则x-y=0或x-3y=0,
所以x=y或x=3y,
当x=y时,=0;
当x=3y时,═==;
综上,=0或
本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.
15.【答案】1
【解析】解:设小路的宽度为xm,根据题意列方程得
(20-x)(10-x)=171,
整理得:x2-30x+29=0
解得:x1=1,x2=29(不合题意,舍去).
故小路的宽度为1m.
16.【答案】3
【解析】解:①解方程x2-x-2=0得,x1=2,x2=-1,得,x1≠2x2,
∴方程x2-x-2=0不是倍根方程;故①不正确;
②若(x-2)(mx+n)=0是倍根方程,x1=2,
因此x2=1或x2=4,
当x2=1时,m+n=0,
当x2=4时,4m+n=0,
∴4m2+5mn+n2=(m+n)(4m+n)=0,
故②正确;
③∵pq=2,则px2+3x+q=(px+1)(x+q)=0,
∴,x2=-q,
∴,
因此是倍根方程,故③正确;
④方程ax2+bx+c=0的根为:,,
若x1=2x2,则,
即,
∴,
∴,
∴,
∴9(b2-4ac)=b2,
∴2b2=9ac.
若2x1=x2时,则,
则,
∴,
∴,
∴,
∴b2=9(b2-4ac),
∴2b2=9ac.
故④正确,
∴正确的有:②③④共3个.
17.【答案】且m≠0
【解析】解:∵△=[2(m-1)]2-4m2=-8m+4≥0,
∴m≤,
?∵x1+x2=-2(m-1)>0,x1x2=m2>0,
∴m<1,m≠0
∴m≤且m≠0.
18.【答案】1或.
【解析】此题考查了勾股定理,利用了分类讨论的思想,熟练掌握勾股定理是解本题的关键.根据题意分三种情况考虑:当∠A=90°;当∠B=90°;当∠APB=90°,根据△ABP为直角三角形,分别求出t的值即可.
解:分三种情况考虑:
①当∠A=90°,即△ABP为直角三角形时,
∵∠BOC>∠A,且∠BOC=60°,
∴∠A≠90°,故此情况不存在;
②当∠B=90°,即△ABP为直角三角形时,如图所示:
∵∠BOC=60°,
∴∠BPO=30°,
∴OP=2OB=2,
∵OP=2t,
∴t=1;
③当∠APB=90°,即△ABP为直角三角形时,过P作PD⊥AB,
∵∠BOC=60°,
∴∠OPD=30°,
∴OD=PO=×2t=t,PD=PO=t,
∴AD=AO+OD=2+t,BD=OB-OD=1-t,即AB=3,
在Rt△ABP中,AP2+BP2=AB2,即(2+t)2+(t)2+(t)2+(1-t)2=32,
解得:t=(负值舍去),
综上,当t=1或t=时,△ABP是直角三角形.
19.【答案】解:(1)(2x+1)2-3(2x+1)=0,
(2x+1)(2x+1-3)=0,
2x+1=0或2x+1-3=0,
所以x1=-,x2=1;
(2)△=(-3)2-4×3×(-1)=21,
x=,
所以x1=,x2=.
【解析】(1)利用因式分解法解方程;
(2)利用求根公式法解方程.
20.【答案】解:(1)△ABC是等腰三角形.理由如下:
∵x=-1是方程的根,
∴(a+c)×(-1)2-2b+(a-c)=0,
∴a+c-2b+a-c=0,
∴a-b=0,∴a=b,
∴△ABC是等腰三角形;
(2)△ABC是直角三角形.理由如下:
∵方程有两个相等的实数根,
∴△=(2b)2-4(a+c)(a-c)=0,
∴4b2-4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形.
【解析】(1)根据方程解的定义把x=-1代入方程得到(a+c)×(-1)2-2b+(a-c)=0,整理得a-b=0,即a=b,于是根据等腰三角形的判定即可得到△ABC是等腰三角形;
(2)根据判别式的意义得到△=(2b)2-4(a+c)(a-c)=0,整理得a2=b2+c2,然后根据勾股定理的逆定理得到△ABC是直角三角形.
21.【答案】解:(1)12;
(2)设剪去的小正方形边长为xcm,由题意可得方程为:
(12-2x)(12-x)=80,
解得:x1=2,x2=16,
又x2=16>12,不合题意,舍去.
答:剪去的小正方形边长为2cm.
【解析】(1)根据图形可知,2a=24,求解即可;
(2)设剪去的小正方形边长为xcm,由题意可得方程(12-2x)(12-x)=80,求解即可.
22.【答案】解:(1)设每天增长的百分率为x,
依题意,得:500(1+x)2=720,
解得:x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:每天增长的百分率为20%;
(2)设应该增加m条生产线,则每条生产线的最大产能为(1500-50m)万件/天,
依题意,得:(1+m)(1500-50m)=6500,
解得:m1=4,m2=25.
又∵在增加产能同时又要节省投入,
∴m=4.
答:应该增加4条生产线.
【解析】(1)设每天增长的百分率为x,根据开工第一天及第三天的产量,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)设应该增加m条生产线,则每条生产线的最大产能为(1500-50m)万件/天,根据每天生产口罩6500万件,即可得出关于m的一元二次方程,解之取其较小值即可得出结论.
23.【答案】解:(1)设x秒后△PBQ的面积等于4cm2,
则BQ=2x,BP=5-x,
根据题意得出:×2x×(5-x)=4,
解得:x1=1,x2=4(不合题意舍去),
答:1秒后△PBQ的面积等于4cm2;
(2)不能,
由题意可得出:×2x×(5-x)=7,
整理得出:x2-5x+7=0,
b2-4ac=25-4×7=-3<0,
∴此方程无实数根,则△PBQ的面积不能等于7.
【解析】(1)设x秒后△PBQ的面积等于4cm2,进而表示出BP,BQ的长,即可得出答案;
(2)根据(1)中解法表示出△PBQ的面积,利用根的判别式,即可得出答案.
24.【答案】解:(1)当a=3,b=4,c=5时,勾系一元二次方程为;
(2)依题意得=()2-4ab=2c2-4ab,
∵a2+b2=c2,
∴2c2-4ab=2(a2+b2)-4ab=2(a-b)2≥0,即≥0,故方程必有实数根;
(3)把x=-1代入得a+b=c,
∵四边形
ACDE
的周长是6,
即2(a+b)+?c=6,
故得到c=2,
∴a2+b2=4,a+b=2,
∵(a+b)2=
a2+b2+2ab,
∴ab=2,
故ABC的面积为ab=1.
【解析】此题主要考查一元二次方程的应用,解题的关键是熟知勾股定理、根的判别式及完全平方公式的应用.
(1)直接找一组勾股数代入方程即可;
(2)根据根的判别式即可求解;
(3)根据方程的解代入求出a,b,c的关系,再根据完全平方公式的变形进行求解.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
八年级数学下册
一元二次方程
单元测试卷
(满分100分)
题号
一
二
三
四
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列方程为一元二次方程的是( )
A.
x2-3=x(x+4)
B.
x2-=3
C.
x2-10x=-5
D.
4x+6xy=33
方程x2=-x的解是(???
)
A.
1
B.
-1
C.
1或0
D.
-1或0
一元二次方程kx2-2x-2=0有实数根,则k的取值范围是( )
A.
k≥-且k≠0
B.
k≥-1
C.
k≤-1且k≠0
D.
k≥-1或k≠0
关于x的方程x2+5x+m=0的一个根为﹣2,则另一个根是(
)
A.
﹣6
B.
﹣3
C.
3
D.
6
等腰三角形的三边均满足方程x2-7x+10=0,该等腰三角形的周长是( )
A.
12
B.
12或9
C.
12或6或15
D.
12或9或6或15
在一次数学兴趣小组活动中,每两名学生握手一次,但小明因中途有事离开,他记得有3人没有和他握过手,经统计所有握手共42次.若设参加活动的学生为x名,据题意可列方程为( )
A.
x(x-1)-3=42
B.
C.
D.
已知(x2+y2+2)(x2+y2+4)=15,则x2+y2的值为( )
A.
-7或1
B.
1
C.
-7
D.
7或-1
一面足够长的墙,用总长为30米的木栅栏图中的虚线围一个矩形场地ABCD,中间用栅栏隔成同样三块,若要围成的矩形面积为54平方米,设垂直于墙的边长为x米,则x的值为(
)
3
B.
4
C.
3或5
D.
3或
若是方程+2x+c=0(a0)的一个根,设M=1-ac,N=,则M与N的大小关系为(
)
A.
M>N
B.
M=N
C.
M
D.
无法确定
定义[x]表示不超过实数x的最大整数,如[1.8]=1、[-1.4]=-2、[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=在-2≤x<2时的解为(?
?
?
)
???????
A.
0或
B.
0或2
C.
1或-
D.
或-
二、填空题(本大题共8小题,共24.0分)
关于x的方程(k+1)x|k-1|+kx+1=0是一元二次方程,则k的值为______
.
已知a是方程x2-3x-1=0的一个根,则代数式-2a2+6a-3的值是______
.
已知方程x2+5x-6=0的解是x1=1,x2=-6,则方程(2x+3)2+5(2x+3)-6=0的解是______
.
已知非零有理数x、y满足x2-4xy+3y2=0,则=______.
如图,在一个长20m,宽10m的矩形草地内修建宽度相等的小路(阴影部分),若剩余草地(空白部分)的面积171m2,则小路的宽度为______m.
如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的有 个.
①方程x2-x-2=0是倍根方程;
②若(x-2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;
③若p、q满足pq=2,则关于x的方程px2+3x+q=0是倍根方程;
④若方程ax2+bx+c=0是倍根方程,则必有2b2=9ac.
关于x的一元二次方程x2+2(m-1)x+m2=0的两个实数根分别为x1,x2,且x1+x2>0,x1x2>0,则m的取值范围是?
?
?
?
?。
如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为____________________.
三、计算题(本大题共1小题,共6.0分)
用适当的方法解下列方程
(1)(2x+1)2=3(2x+1)
(2)3x2-3x-1=0.
四、解答题(本大题共5小题,共40.0分)
已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
如图是一张长24
cm,宽12
cm的矩形铁皮,将其剪去一个小正方形和两个矩形,剩余部分(阴影部分)恰好可制成一个有盖的长方体铁盒.
(1)a=________;
(2)若铁盒底面积是80
cm2,求剪去的小正方形边长.
随着全球疫情的爆发,医疗物资的极度匮乏,中国许多企业都积极的宣布生产医疗物资以应对疫情,某工厂及时引进了一条口罩生产线生产口罩,开工第一天生产500万个,第三天生产720万个,若每天增长的百分率相同.试回答下列问题:
(1)求每天增长的百分率;
(2)经调查发现,1条生产线最大产能是1500万个/天,若每增加1条生产线,每条生产线的最大产能将减少50万个/天,现该厂要保证每天生产口罩6500万件,在增加产能同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
如图,在△ABC中.∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果点P、Q分别从A、B同时出发,那么几秒后△PBQ的面积等于4cm2?
(2)在(1)中△PBQ的面积能否等于7?请说明理由.
如图,四边形
ACDE
是证明勾股定理时用到的一个图形,a
、b
、c
是
Rt△ABC和
Rt△BED
的边长,已知,这时我们把关于
x
的形如二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于
x
的“勾系一元二次方程”,必有实数根;
(3)若
x
=-1是“勾系一元二次方程”的一个根,且四边形
ACDE
的周长是6,求△ABC
的面积.
答案和解析
1.【答案】C
【解析】解:A、方程化简得:4x+3=0,是一元一次方程,不符合题意;
B、x2-=3为分式方程,不符合题意;
C、x2-10x=-5是一元二次方程,符合题意;
D、4x+6xy=5是二元二次方程,不符合题意.
2.【答案】D
【解析】解:方程
x2=-x,
移项,x2+x=0,
提公因式,x(x+1)=0,
得,x=0,x+1=0,
解得,x1=0,x2=-1
3.【答案】A
【解析】解:∵一元二次方程kx2-2x-2=0有实数根,
∴△=b2-4ac=(-2)2-4k×(-2)=4+8k≥0,k≠0,
解得:k≥-且k≠0
本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.
4.【答案】B
【解析】解:设方程的另一个根为n,
则有-2+n=-5,
解得:n=-3.
本题考查了根与系数的关系,牢记两根之和等于-、两根之积等于是解题的关键.
5.【答案】C
【解析】解:∵x2-7x+10=0,
∴(x-2)(x-5)=0.
∴x-2=0或x-5=0.
解得x=2或x=5.
当等腰三角形的腰长为2,底长为5时,由于2+2<5,构不成三角形;
当等腰三角形的腰长为2,底长为2时,该等腰三角形的周长为2+2+2=6;
当等腰三角形的腰长为5,底长为2时,该等腰三角形的周长为:5+5+2=12;
当等腰三角形的腰长为5,底长为5时,该等腰三角形的周长为:5+5+5=15.
先求解一元二次方程,再根据等腰三角形分类讨论.
6.【答案】C
【解析】解:参加此会的学生为x名,每个学生都要握手(x-1)次,
∴可列方程为x(x-1)-3=42
每个学生都要和他自己以外的学生握手一次,但两个学生之间只握手一次,所以等量关系为:×学生数×(学生数-1)=总握手次数,把相关数值代入即可求解.
7.【答案】B
【解析】解:设t=x2+y2(t≥0),则原方程转化为(t+2)(t+4)=15,
整理,得(t+7)(t-1)=0.
解得t=-7(舍去)或t=1.
所以x2+y2的值为1.
本题主要考查了换元法解一元二次方程,换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理.
8.【答案】D
【解析】解:设垂直于墙的边长为x米,由题意可得,
x(30-4x)=54,整理得:2x2-15x+27=0,
解得:x1=4.5,x2=3,
即x的值为:3或4.5.
9.【答案】B
【解析】把x0代入方程ax2+2x+c=0得ax02+2x0=-c,作差法比较可得.
解:∵x0是方程ax2+2x+c=0(a≠0)的一个根,
∴ax02+2x0+c=0,即ax02+2x0=-c,
则N-M=(ax0+1)2-(1-ac)
=a2x02+2ax0+1-1+ac
=a(ax02+2x0)+ac
=-ac+ac
=0,∴M=N.
10.【答案】A
【解析】本题主要考查的是新定义,函数的图象的有关知识,根据新定义和函数图象讨论;然后分别解关于x的一元二次方程即可.
解:当1x<2时,=1,解得=,=-(舍去);
当0x<1时,=0,解得x=0;
当-1x<0时,=-1,方程没有实数解;
当-2x<-1时,=-2,方程没有实数解;
所以方程[x]=的解为0或
11.【答案】3
【解析】解:由题意得,,
解得k=3.
一元二次方程必须满足两个条件:(1)未知数的最高次数是2;(2)二次项系数不为0.由这两个条件得到相应的关系式,再求解即可.
12.【答案】-5
【解析】解:∵a是方程x2-3x-1=0的一个根,
∴a2-3a-1=0,
整理得,a2-3a=1,
∴-2a2+6a-3=-2(a2-3a)-3
=-2×1-3
=-5
根据方程的根的定义,把x=a代入方程求出a2-3a的值,然后整体代入代数式进行计算即可得解.
13.【答案】x1=-1,x2=-
【解析】解:把方程(2x+3)2+5(2x+3)-6=0看作关于2x+3的一元二次方程,
所以2x+3=1或2x+3=-6,
所以x1=-1,x2=-.
14.【答案】0或
【解析】解:∵非零有理数x、y满足x2-4xy+3y2=0,
∴(x-y)(x-3y)=0,
则x-y=0或x-3y=0,
所以x=y或x=3y,
当x=y时,=0;
当x=3y时,═==;
综上,=0或
本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.
15.【答案】1
【解析】解:设小路的宽度为xm,根据题意列方程得
(20-x)(10-x)=171,
整理得:x2-30x+29=0
解得:x1=1,x2=29(不合题意,舍去).
故小路的宽度为1m.
16.【答案】3
【解析】解:①解方程x2-x-2=0得,x1=2,x2=-1,得,x1≠2x2,
∴方程x2-x-2=0不是倍根方程;故①不正确;
②若(x-2)(mx+n)=0是倍根方程,x1=2,
因此x2=1或x2=4,
当x2=1时,m+n=0,
当x2=4时,4m+n=0,
∴4m2+5mn+n2=(m+n)(4m+n)=0,
故②正确;
③∵pq=2,则px2+3x+q=(px+1)(x+q)=0,
∴,x2=-q,
∴,
因此是倍根方程,故③正确;
④方程ax2+bx+c=0的根为:,,
若x1=2x2,则,
即,
∴,
∴,
∴,
∴9(b2-4ac)=b2,
∴2b2=9ac.
若2x1=x2时,则,
则,
∴,
∴,
∴,
∴b2=9(b2-4ac),
∴2b2=9ac.
故④正确,
∴正确的有:②③④共3个.
17.【答案】且m≠0
【解析】解:∵△=[2(m-1)]2-4m2=-8m+4≥0,
∴m≤,
?∵x1+x2=-2(m-1)>0,x1x2=m2>0,
∴m<1,m≠0
∴m≤且m≠0.
18.【答案】1或.
【解析】此题考查了勾股定理,利用了分类讨论的思想,熟练掌握勾股定理是解本题的关键.根据题意分三种情况考虑:当∠A=90°;当∠B=90°;当∠APB=90°,根据△ABP为直角三角形,分别求出t的值即可.
解:分三种情况考虑:
①当∠A=90°,即△ABP为直角三角形时,
∵∠BOC>∠A,且∠BOC=60°,
∴∠A≠90°,故此情况不存在;
②当∠B=90°,即△ABP为直角三角形时,如图所示:
∵∠BOC=60°,
∴∠BPO=30°,
∴OP=2OB=2,
∵OP=2t,
∴t=1;
③当∠APB=90°,即△ABP为直角三角形时,过P作PD⊥AB,
∵∠BOC=60°,
∴∠OPD=30°,
∴OD=PO=×2t=t,PD=PO=t,
∴AD=AO+OD=2+t,BD=OB-OD=1-t,即AB=3,
在Rt△ABP中,AP2+BP2=AB2,即(2+t)2+(t)2+(t)2+(1-t)2=32,
解得:t=(负值舍去),
综上,当t=1或t=时,△ABP是直角三角形.
19.【答案】解:(1)(2x+1)2-3(2x+1)=0,
(2x+1)(2x+1-3)=0,
2x+1=0或2x+1-3=0,
所以x1=-,x2=1;
(2)△=(-3)2-4×3×(-1)=21,
x=,
所以x1=,x2=.
【解析】(1)利用因式分解法解方程;
(2)利用求根公式法解方程.
20.【答案】解:(1)△ABC是等腰三角形.理由如下:
∵x=-1是方程的根,
∴(a+c)×(-1)2-2b+(a-c)=0,
∴a+c-2b+a-c=0,
∴a-b=0,∴a=b,
∴△ABC是等腰三角形;
(2)△ABC是直角三角形.理由如下:
∵方程有两个相等的实数根,
∴△=(2b)2-4(a+c)(a-c)=0,
∴4b2-4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形.
【解析】(1)根据方程解的定义把x=-1代入方程得到(a+c)×(-1)2-2b+(a-c)=0,整理得a-b=0,即a=b,于是根据等腰三角形的判定即可得到△ABC是等腰三角形;
(2)根据判别式的意义得到△=(2b)2-4(a+c)(a-c)=0,整理得a2=b2+c2,然后根据勾股定理的逆定理得到△ABC是直角三角形.
21.【答案】解:(1)12;
(2)设剪去的小正方形边长为xcm,由题意可得方程为:
(12-2x)(12-x)=80,
解得:x1=2,x2=16,
又x2=16>12,不合题意,舍去.
答:剪去的小正方形边长为2cm.
【解析】(1)根据图形可知,2a=24,求解即可;
(2)设剪去的小正方形边长为xcm,由题意可得方程(12-2x)(12-x)=80,求解即可.
22.【答案】解:(1)设每天增长的百分率为x,
依题意,得:500(1+x)2=720,
解得:x1=0.2=20%,x2=-2.2(不合题意,舍去).
答:每天增长的百分率为20%;
(2)设应该增加m条生产线,则每条生产线的最大产能为(1500-50m)万件/天,
依题意,得:(1+m)(1500-50m)=6500,
解得:m1=4,m2=25.
又∵在增加产能同时又要节省投入,
∴m=4.
答:应该增加4条生产线.
【解析】(1)设每天增长的百分率为x,根据开工第一天及第三天的产量,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)设应该增加m条生产线,则每条生产线的最大产能为(1500-50m)万件/天,根据每天生产口罩6500万件,即可得出关于m的一元二次方程,解之取其较小值即可得出结论.
23.【答案】解:(1)设x秒后△PBQ的面积等于4cm2,
则BQ=2x,BP=5-x,
根据题意得出:×2x×(5-x)=4,
解得:x1=1,x2=4(不合题意舍去),
答:1秒后△PBQ的面积等于4cm2;
(2)不能,
由题意可得出:×2x×(5-x)=7,
整理得出:x2-5x+7=0,
b2-4ac=25-4×7=-3<0,
∴此方程无实数根,则△PBQ的面积不能等于7.
【解析】(1)设x秒后△PBQ的面积等于4cm2,进而表示出BP,BQ的长,即可得出答案;
(2)根据(1)中解法表示出△PBQ的面积,利用根的判别式,即可得出答案.
24.【答案】解:(1)当a=3,b=4,c=5时,勾系一元二次方程为;
(2)依题意得=()2-4ab=2c2-4ab,
∵a2+b2=c2,
∴2c2-4ab=2(a2+b2)-4ab=2(a-b)2≥0,即≥0,故方程必有实数根;
(3)把x=-1代入得a+b=c,
∵四边形
ACDE
的周长是6,
即2(a+b)+?c=6,
故得到c=2,
∴a2+b2=4,a+b=2,
∵(a+b)2=
a2+b2+2ab,
∴ab=2,
故ABC的面积为ab=1.
【解析】此题主要考查一元二次方程的应用,解题的关键是熟知勾股定理、根的判别式及完全平方公式的应用.
(1)直接找一组勾股数代入方程即可;
(2)根据根的判别式即可求解;
(3)根据方程的解代入求出a,b,c的关系,再根据完全平方公式的变形进行求解.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
