2.3 一元二次方程的应用同步练习(含解析)
文档属性
| 名称 | 2.3 一元二次方程的应用同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-23 08:35:36 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版八年级下册2.3
一元二次方程的应用
同步练习
一、单选题(共4题;共8分)
1.某班学生毕业时,都将自己的照片向本班其他同学送一张留念,全班一共送了1260张,如果全班有x名同学,根据题意,列出方程为(??
)
A.?x(x+1)=1260????????B.?2x(x+1)=1260????????C.?x(x﹣1)=1260????????D.?x(x﹣1)=1260×2
2.为了美化校园环境,某区第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元,设前三个季度用于绿化投资的平均增长率为x.那么x满足的方程为(?
)
A.?18
(1+2x)=90???????????????????????????????????????????????B.?18
(1+x)
2=90
C.?18+18
(1+x)+18
(1+2x)=90???????????????????D.?18+18
(1+x)+18
(1+x)
2=90
3.某种花卉每盆的盈利与每盆所植的株数有一定的关系,每盆植5株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少1元,要使每盆的盈利达到14元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是(???
)
A.?(5+x)(4-x)=14???????????????B.?(x+5)(4+x)=14???????????????C.?(x+4)(5-x)=14???????????????D.?(x+1)(4-x)=14
4.如图,在一块长为
,宽为
的矩形
空地内修建四条宽度相等,且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的4倍,道路占地总面积为
.设道路宽为
,则以下方程正确的是(??
)
A.???????????????B.???????????????C.???????????????D.?
二、填空题(共5题;共5分)
5.一个两位数,它的数值等于它的个位上的数字的平方的3倍,它的十位数字比个位数字大2.若设个位数字为x
,
列出求该两位数的方程式为________.
6.有一人患流感,经过两轮传染后共有81人患了流感,则每轮传染中平均一人传染了________人.
7.某工厂七月份产值是
万元,计划九月份的产值要达到
万元,如果每月的产值的增长率相同,则增长率为________.
8.某服装店经销一种品牌服装,平均每天可销售20件,每件赢利44元,经市场预测发现:在每件降价不超过10元的情况下,若每件降价1元,则每天可多销售5件,若该专卖店要使该品牌服装每天的赢利为1600元,则每件应降价____________元.
9.如图,在工地边的靠墙处,
用
米长的铁栅栏围一个占地面积为
平方米的长方形临时仓库,并在其中一边上留宽为
米的大门,设无门的那边长为
米.根据题意,可建立关于x的方程是________.
三、综合题(共6题;共60分)
10.为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请x个好友转发,每个好友转发之后,又邀请x个互不相同的好友转发,已知经过两轮转发后,共有111个人参与了本次活动。
(1)x的值是多少?
(2)再经过几轮转发后,参与人数会超过10000人?
11.把一个足球垂直地面向上踢,t(秒)后该足球的高度h(米)适用公式h=20t-5t2
(1)经过多少秒足球重新回到地面?
(2)经过多少秒足球的高度为15米?
12.自2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日这天猪肉售价为每千克56元,比去年同一天上涨了40%.
(1)求2019年1月10日,该超市猪肉的售价为每千克多少元?
(2)现在某超市以每千克46元的价格购进猪肉,按2020年月10日价格出售,平均一天能销售100千克.
为促进消费,超市决定对这批猪肉进行降价销售,经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加18千克.为了实现平均每天有950元的销售利润,超市应将每千克猪肉定为多少元?
13.某市一楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套200平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.5折销售;②不打折,送2年物业管理费,物业管理费为每平方米每月5元,请问哪种方案更优惠?
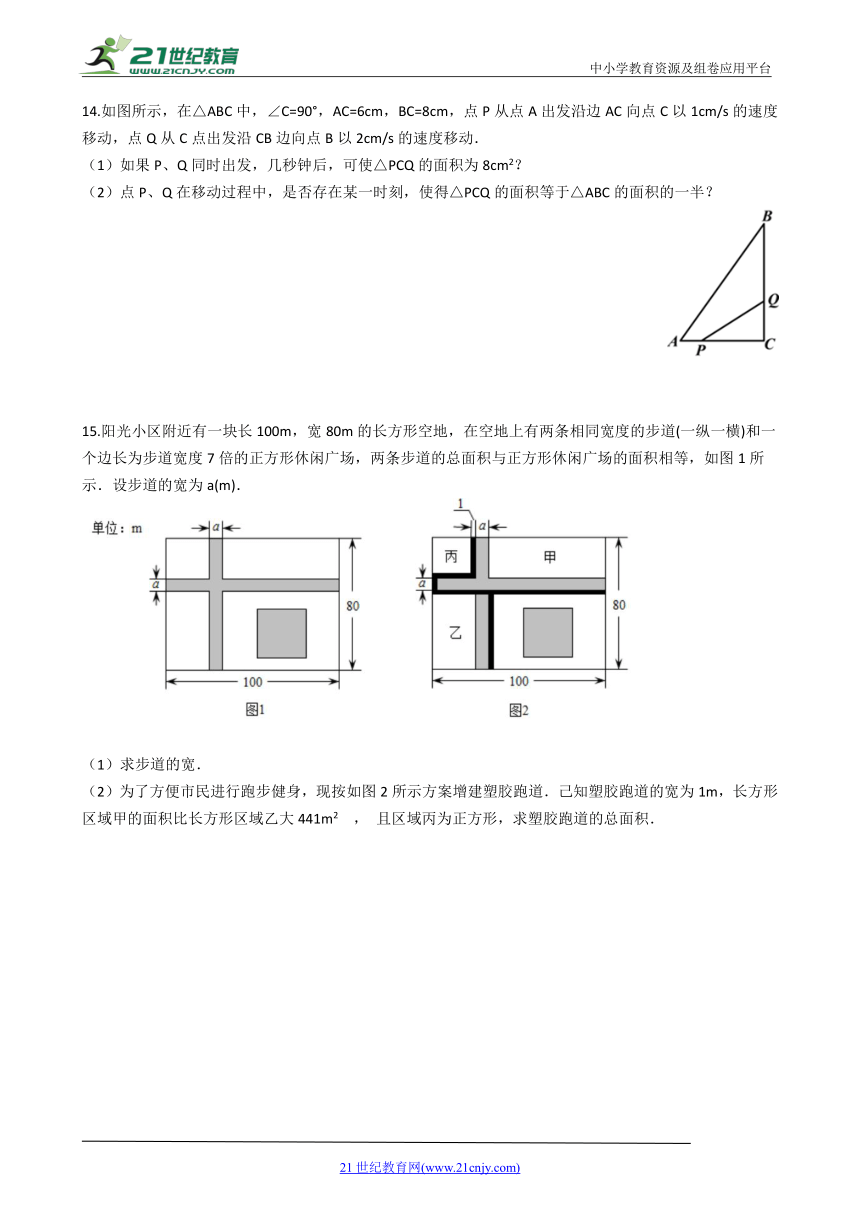
14.如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半?
15.阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).
?
(1)求步道的宽.
(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2
,
且区域丙为正方形,求塑胶跑道的总面积.
答案解析部分
一、单选题
1.【答案】
C
【解答】解:依题意,得:x(x﹣1)=1260.
故答案为:C.
2.【答案】
D
【解答】解:设前三个季度用于绿化投资的平均增长率为x,那么依题意得:
18+18
+18
=90.
故答案为:D.
3.【答案】
A
【解答】
设每盆多植x株
,则每盆共有(x+5)株,
∴平均每株盈利(4-x)元,
∴(x+5)(4-x)=14.
故答案为A.
4.【答案】
B
【解答】解:设道路宽为x
m,则中间正方形的边长为4x
m,
依题意,得:x(20+4x+12+4x)=40,
即32x+8x2=40.
故答案为:B.
二、填空题
5.【答案】
10(x+2)+x=3x2
【解答】解:设个位数字为x,则这个数为3x2
,
十位数字为x+2,
由题意得,10(x+2)+x=3x2
.
故答案为10(x+2)+x=3x2
.
6.【答案】
8
【解答】设每轮传染中平均一个人传染了x人,则:1+x+(1+x)x=81,
,∴
(舍去)
答:每轮传染中平均一个人传染了8人.
7.【答案】
【解答】解:设增长率为
.
,
,
,
.
故每月的增长率是
.
故答案是:
.
8.【答案】
4
【解答】解:设每件应降价x元,根据题意得
(20+5x)(44-x)=1600
解之:x1=36,x2=4.
∵x≤10
∴x=4
故答案为:4.
9.【答案】
【解答】解:设无门的那边长为x米,根据题意得:
,即
;
故答案为
.
三、综合题
10.【答案】
(1)解:一轮转发之后有(x+1)人参与,两轮转发之后有(1+x+x?)人参与,
故根据题意可得1+x+x?=111,
解得x1=10,x2=-11(舍),
故x的值为10
(2)解:三轮转发之后,参与人数为1+10+100+1000=1111(人),
四轮转发之后,参与人数为1+10+100+1000+10000=11111(人),大于10000人,所以再经过两轮转发后,参与人数会超过10000人。
11.【答案】
(1)解:当h=0时,足球重新回到地面
即20t-5t2=0,解得
∴经过4秒足球重新回到地面
(2)解:当20t-5t2=15时,解得
∴经过1秒或者3秒足球的高度为15米
12.【答案】
(1)解:设该超市猪肉的价格为每千克
元,
根据题意得:
解得:
答:2019年1月10日,该超市猪肉的价格为每千克40元
(2)解:设每千克猪肉下降
元,则
解得:
,
(舍去)
所以:
(元)
答:每千克猪肉应该定价为51元.
13.【答案】
(1)解:设平均每次降价的百分率是
,依题意得
解得:
(不合题意,舍去)
答:平均每次降价的百分率为
.
(2)解:方案①的房款是
(元)
方案②的房款是:
(元)
答:选方案①更优惠.
14.【答案】
(1)解:设xs后,可使△PCQ的面积为8cm2
.
由题意得,AP=xcm,PC=(6-x)cm,CQ=2xcm,
则
?(6?x)?2x=8.
整理,得x2-6x+8=0,解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2
.
(2)解:由题意得:
S△ABC=
×AC?BC=
×6×8=24,
即:
×2x×(6-x)=
×24,
x2-6x+12=0,
△=62-4×12=-12<0,该方程无实数解,
所以,不存在使得△PCQ的面积等于△ABC的面积的一半的时刻.
15.【答案】
(1)解:由题意,得100a+80a-a2=(7a)2
,
化简,得a2=3.6a,
∵a>0,
∴a=3.6.
答:步道的宽为3.6
m.
(2)解:如图,
由题意,得AB-DE=100-80+1=21(m),
∴BC=EF=
=21(m).
∴塑胶跑道的总面积为1×(100+80+21-2)=199(m2).
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版八年级下册2.3
一元二次方程的应用
同步练习
一、单选题(共4题;共8分)
1.某班学生毕业时,都将自己的照片向本班其他同学送一张留念,全班一共送了1260张,如果全班有x名同学,根据题意,列出方程为(??
)
A.?x(x+1)=1260????????B.?2x(x+1)=1260????????C.?x(x﹣1)=1260????????D.?x(x﹣1)=1260×2
2.为了美化校园环境,某区第一季度用于绿化的投资为18万元,前三个季度用于绿化的总投资为90万元,设前三个季度用于绿化投资的平均增长率为x.那么x满足的方程为(?
)
A.?18
(1+2x)=90???????????????????????????????????????????????B.?18
(1+x)
2=90
C.?18+18
(1+x)+18
(1+2x)=90???????????????????D.?18+18
(1+x)+18
(1+x)
2=90
3.某种花卉每盆的盈利与每盆所植的株数有一定的关系,每盆植5株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少1元,要使每盆的盈利达到14元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是(???
)
A.?(5+x)(4-x)=14???????????????B.?(x+5)(4+x)=14???????????????C.?(x+4)(5-x)=14???????????????D.?(x+1)(4-x)=14
4.如图,在一块长为
,宽为
的矩形
空地内修建四条宽度相等,且与矩形各边垂直的道路.四条道路围成的中间部分恰好是一个正方形,且边长是道路宽的4倍,道路占地总面积为
.设道路宽为
,则以下方程正确的是(??
)
A.???????????????B.???????????????C.???????????????D.?
二、填空题(共5题;共5分)
5.一个两位数,它的数值等于它的个位上的数字的平方的3倍,它的十位数字比个位数字大2.若设个位数字为x
,
列出求该两位数的方程式为________.
6.有一人患流感,经过两轮传染后共有81人患了流感,则每轮传染中平均一人传染了________人.
7.某工厂七月份产值是
万元,计划九月份的产值要达到
万元,如果每月的产值的增长率相同,则增长率为________.
8.某服装店经销一种品牌服装,平均每天可销售20件,每件赢利44元,经市场预测发现:在每件降价不超过10元的情况下,若每件降价1元,则每天可多销售5件,若该专卖店要使该品牌服装每天的赢利为1600元,则每件应降价____________元.
9.如图,在工地边的靠墙处,
用
米长的铁栅栏围一个占地面积为
平方米的长方形临时仓库,并在其中一边上留宽为
米的大门,设无门的那边长为
米.根据题意,可建立关于x的方程是________.
三、综合题(共6题;共60分)
10.为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请x个好友转发,每个好友转发之后,又邀请x个互不相同的好友转发,已知经过两轮转发后,共有111个人参与了本次活动。
(1)x的值是多少?
(2)再经过几轮转发后,参与人数会超过10000人?
11.把一个足球垂直地面向上踢,t(秒)后该足球的高度h(米)适用公式h=20t-5t2
(1)经过多少秒足球重新回到地面?
(2)经过多少秒足球的高度为15米?
12.自2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日这天猪肉售价为每千克56元,比去年同一天上涨了40%.
(1)求2019年1月10日,该超市猪肉的售价为每千克多少元?
(2)现在某超市以每千克46元的价格购进猪肉,按2020年月10日价格出售,平均一天能销售100千克.
为促进消费,超市决定对这批猪肉进行降价销售,经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加18千克.为了实现平均每天有950元的销售利润,超市应将每千克猪肉定为多少元?
13.某市一楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套200平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.5折销售;②不打折,送2年物业管理费,物业管理费为每平方米每月5元,请问哪种方案更优惠?
14.如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8cm2?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半?
15.阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).
?
(1)求步道的宽.
(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2
,
且区域丙为正方形,求塑胶跑道的总面积.
答案解析部分
一、单选题
1.【答案】
C
【解答】解:依题意,得:x(x﹣1)=1260.
故答案为:C.
2.【答案】
D
【解答】解:设前三个季度用于绿化投资的平均增长率为x,那么依题意得:
18+18
+18
=90.
故答案为:D.
3.【答案】
A
【解答】
设每盆多植x株
,则每盆共有(x+5)株,
∴平均每株盈利(4-x)元,
∴(x+5)(4-x)=14.
故答案为A.
4.【答案】
B
【解答】解:设道路宽为x
m,则中间正方形的边长为4x
m,
依题意,得:x(20+4x+12+4x)=40,
即32x+8x2=40.
故答案为:B.
二、填空题
5.【答案】
10(x+2)+x=3x2
【解答】解:设个位数字为x,则这个数为3x2
,
十位数字为x+2,
由题意得,10(x+2)+x=3x2
.
故答案为10(x+2)+x=3x2
.
6.【答案】
8
【解答】设每轮传染中平均一个人传染了x人,则:1+x+(1+x)x=81,
,∴
(舍去)
答:每轮传染中平均一个人传染了8人.
7.【答案】
【解答】解:设增长率为
.
,
,
,
.
故每月的增长率是
.
故答案是:
.
8.【答案】
4
【解答】解:设每件应降价x元,根据题意得
(20+5x)(44-x)=1600
解之:x1=36,x2=4.
∵x≤10
∴x=4
故答案为:4.
9.【答案】
【解答】解:设无门的那边长为x米,根据题意得:
,即
;
故答案为
.
三、综合题
10.【答案】
(1)解:一轮转发之后有(x+1)人参与,两轮转发之后有(1+x+x?)人参与,
故根据题意可得1+x+x?=111,
解得x1=10,x2=-11(舍),
故x的值为10
(2)解:三轮转发之后,参与人数为1+10+100+1000=1111(人),
四轮转发之后,参与人数为1+10+100+1000+10000=11111(人),大于10000人,所以再经过两轮转发后,参与人数会超过10000人。
11.【答案】
(1)解:当h=0时,足球重新回到地面
即20t-5t2=0,解得
∴经过4秒足球重新回到地面
(2)解:当20t-5t2=15时,解得
∴经过1秒或者3秒足球的高度为15米
12.【答案】
(1)解:设该超市猪肉的价格为每千克
元,
根据题意得:
解得:
答:2019年1月10日,该超市猪肉的价格为每千克40元
(2)解:设每千克猪肉下降
元,则
解得:
,
(舍去)
所以:
(元)
答:每千克猪肉应该定价为51元.
13.【答案】
(1)解:设平均每次降价的百分率是
,依题意得
解得:
(不合题意,舍去)
答:平均每次降价的百分率为
.
(2)解:方案①的房款是
(元)
方案②的房款是:
(元)
答:选方案①更优惠.
14.【答案】
(1)解:设xs后,可使△PCQ的面积为8cm2
.
由题意得,AP=xcm,PC=(6-x)cm,CQ=2xcm,
则
?(6?x)?2x=8.
整理,得x2-6x+8=0,解得x1=2,x2=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8cm2
.
(2)解:由题意得:
S△ABC=
×AC?BC=
×6×8=24,
即:
×2x×(6-x)=
×24,
x2-6x+12=0,
△=62-4×12=-12<0,该方程无实数解,
所以,不存在使得△PCQ的面积等于△ABC的面积的一半的时刻.
15.【答案】
(1)解:由题意,得100a+80a-a2=(7a)2
,
化简,得a2=3.6a,
∵a>0,
∴a=3.6.
答:步道的宽为3.6
m.
(2)解:如图,
由题意,得AB-DE=100-80+1=21(m),
∴BC=EF=
=21(m).
∴塑胶跑道的总面积为1×(100+80+21-2)=199(m2).
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
