1.1 锐角三角函数 同步练习(含解析)
文档属性
| 名称 | 1.1 锐角三角函数 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 364.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册1.1
锐角三角函数
同步练习
一、单选题(共8题;共24分)
1.已知
为锐角,且
,则
的度数为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
2.在Rt△ABC中,各边都扩大5倍,则锐角A的正切函数值(??
)
A.?不变???????????????????????????????B.?扩大5倍???????????????????????????????C.?缩小5倍???????????????????????????????D.?不能确定
3.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边AC的长是(??
)
?m·sin35°?????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?m·cos35°
(第3题)
(第4题)
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论错误的是(?
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
5.若∠A是锐角,且sinA=
,则(?????
)
A.?0?<∠A<30???????????????????B.?30?<∠A<45???????????????????C.?45?<∠A<60???????????????????D.?60?<∠A<90?
6.在Rt△ABC中,∠C=90°,若sinA=
,
则tanB=(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
7.如图,以
为圆心,任意长为半径画弧,与射线
交于点
,再以
为圆心,
长为半径画弧,两弧交于点
画射线
,则
的值为(
??)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
8.在△ABC中,AB=12
,AC=13,cosB=
,则BC的边长为(
??)
A.?7??????????????????????????????????????B.?8??????????????????????????????????????C.?8或17??????????????????????????????????????D.?7或17
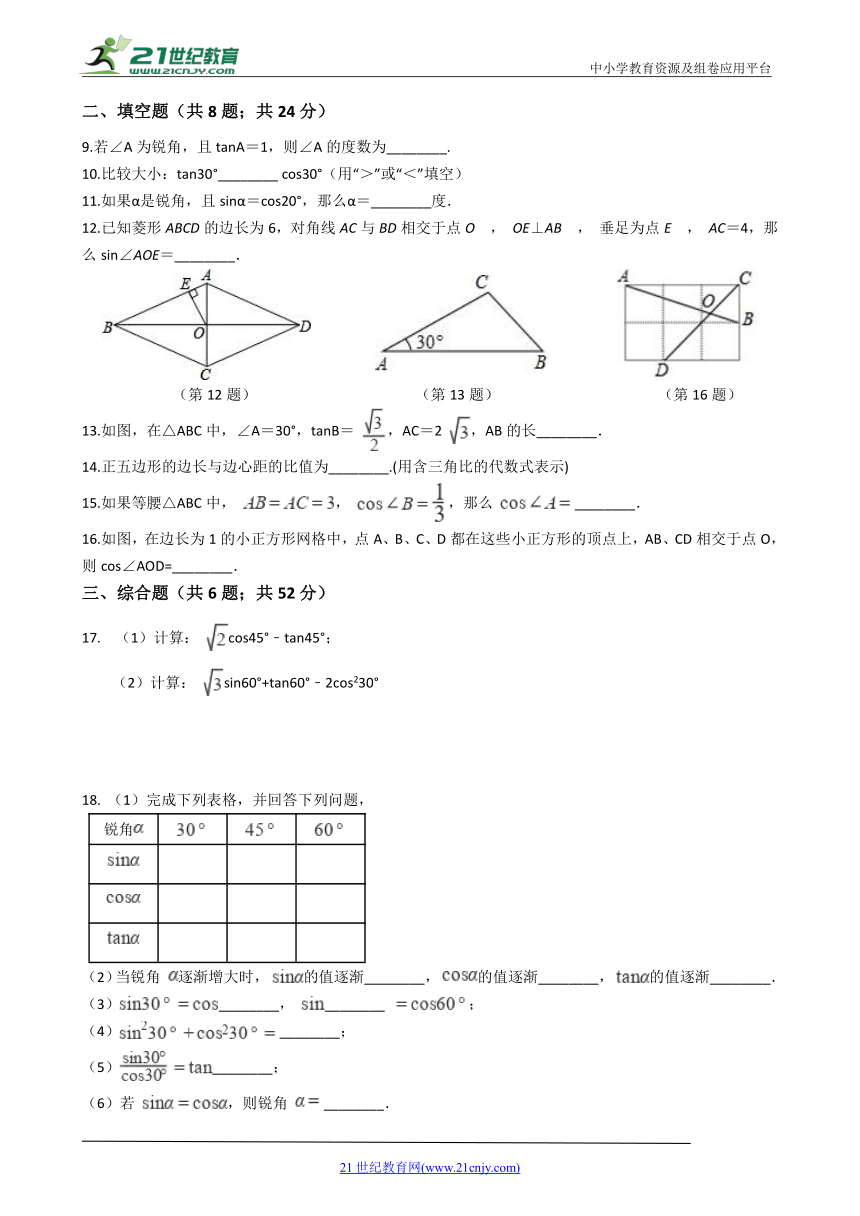
二、填空题(共8题;共24分)
9.若∠A为锐角,且tanA=1,则∠A的度数为________.
10.比较大小:tan30°________
cos30°(用“>”或“<”填空)
11.如果α是锐角,且sinα=cos20°,那么α=________度.
12.已知菱形ABCD的边长为6,对角线AC与BD相交于点O
,
OE⊥AB
,
垂足为点E
,
AC=4,那么sin∠AOE=________.
(第12题)
(第13题)
(第16题)
13.如图,在△ABC中,∠A=30°,tanB=
,AC=2
,AB的长________.
14.正五边形的边长与边心距的比值为________.(用含三角比的代数式表示)
15.如果等腰△ABC中,
,
,那么
________.
16.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD=________.
三、综合题(共6题;共52分)
17.??
(1)计算:
cos45°﹣tan45°;
(2)计算:
sin60°+tan60°﹣2cos230°
18.??(1)完成下列表格,并回答下列问题,
锐角
(2)当锐角
逐渐增大时,
的值逐渐________,
的值逐渐________,
的值逐渐________.
(3)________,
________
;
(4)________;
(5)________;
(6)若
,则锐角
________.
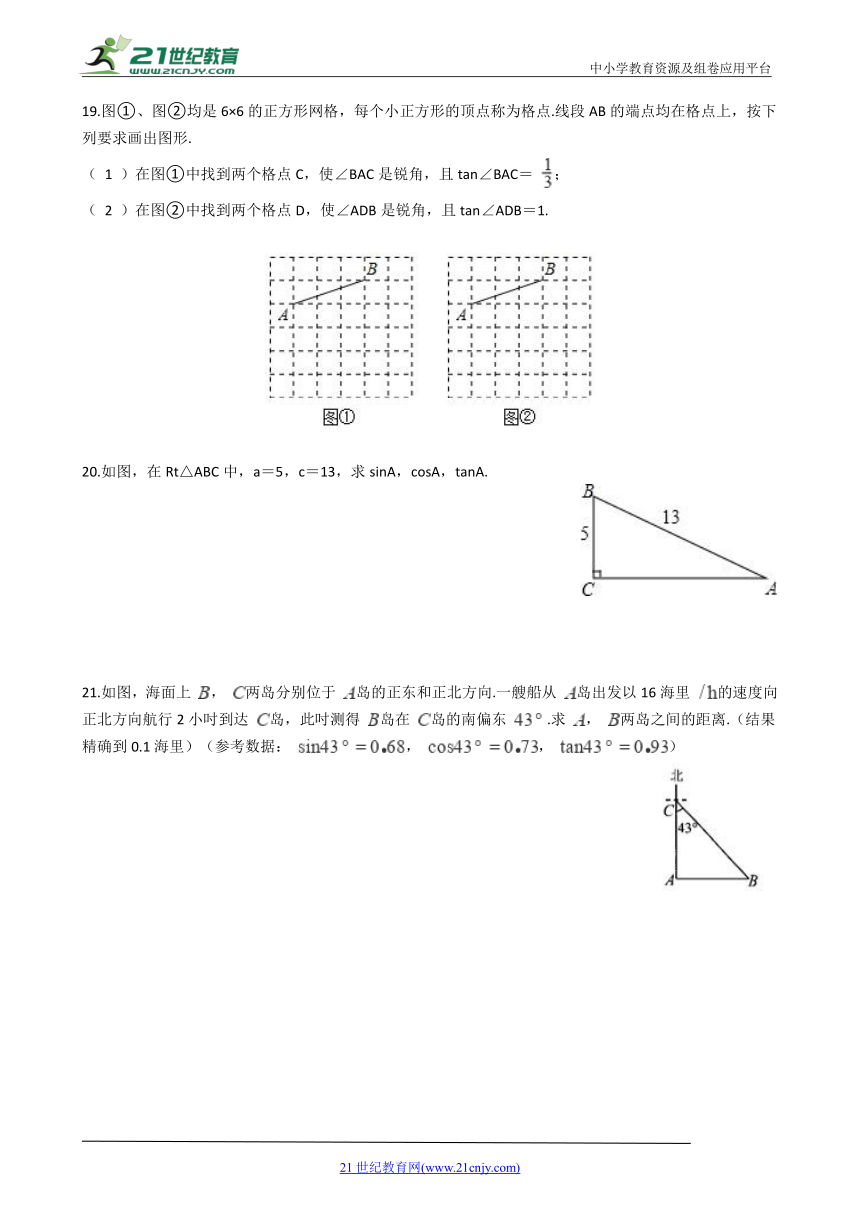
19.图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形.
(
1
)在图①中找到两个格点C,使∠BAC是锐角,且tan∠BAC=
;
(
2
)在图②中找到两个格点D,使∠ADB是锐角,且tan∠ADB=1.
20.如图,在Rt△ABC中,a=5,c=13,求sinA,cosA,tanA.
21.如图,海面上
,
两岛分别位于
岛的正东和正北方向.一艘船从
岛出发以16海里
的速度向正北方向航行2小吋到达
岛,此吋测得
岛在
岛的南偏东
.求
,
两岛之间的距离.(结果精确到0.1海里)(参考数据:
,
,
)
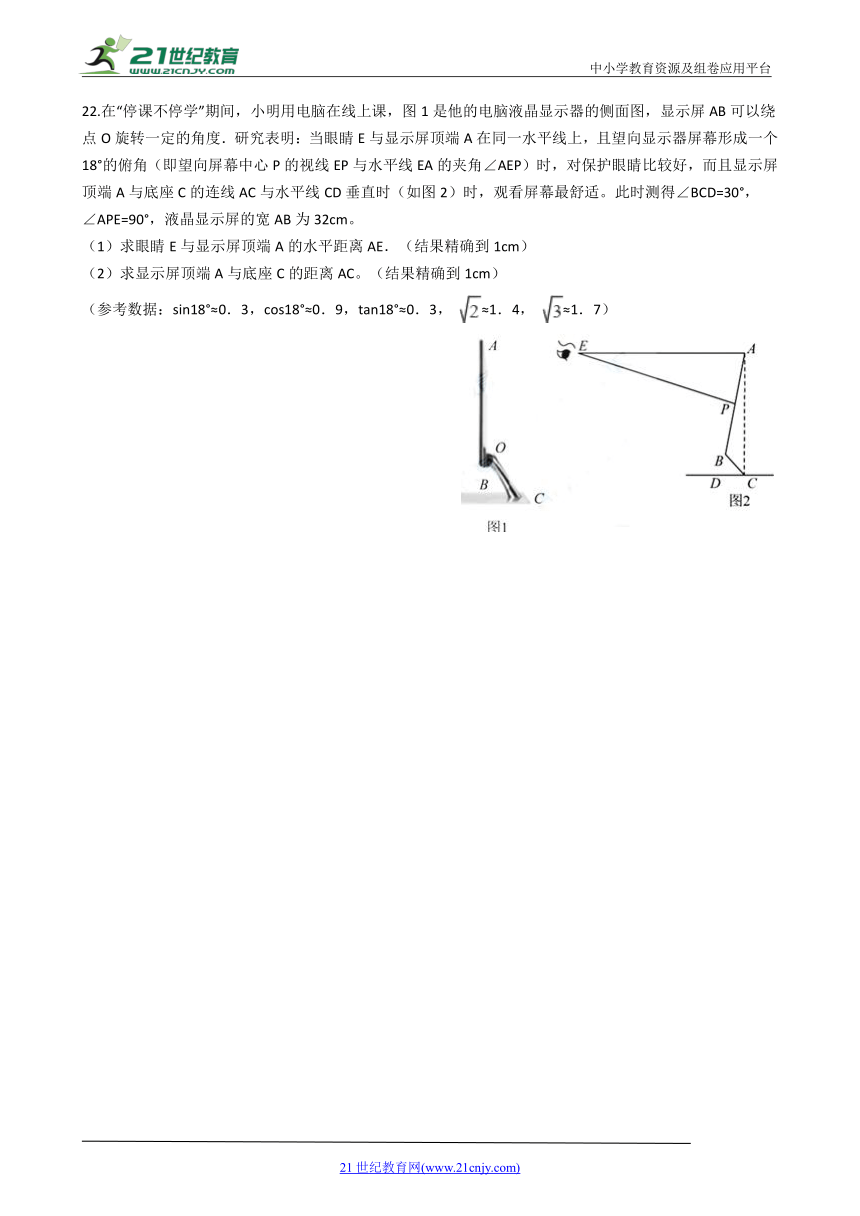
22.在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕点O旋转一定的角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°的俯角(即望向屏幕中心P的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适。此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm。
(1)求眼睛E与显示屏顶端A的水平距离AE.(结果精确到1cm)
(2)求显示屏顶端A与底座C的距离AC。(结果精确到1cm)
(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,
≈1.4,
≈1.7)
答案解析部分
一、单选题
1.【答案】
B
【解答】解:
为锐角,且
,
.
故答案为:
.
2.【答案】
A
【解答】解:因为三角函数值与对应边的比值有关,所以各边的长度都扩大5倍后,锐有A的各三角函数值没有变化.
故答案为:A.
3.【答案】
D
【解答】解:在Rt△ABC中,
AB=m,∠A=35°,
,
∴AC=
,
故答案为:D.
4.【答案】
C
【解答】解:在Rt△ABC中,∠BAC=90°,sinB=
,B符合题意
∵AD⊥BC,∴sinB=
,A符合题意
sinB=sin∠DAC=
,D符合题意
综上,只有C不符合题意
故答案为:C.
5.【答案】
A
【解答】解:∵sin30°=
又∵0<<
∴0°<∠A<30°
故答案为:A.
6.【答案】
C
【解答】解:∵sinA=,
0∴cosA===,
∵A+B=90°,
∴sinB=cosA,cosB=sinA,
∴.
故答案为:C.
7.【答案】
D
【解答】解:如图,连结BC,
则由题意可得OC=OB,CB=OB,∴OC=OB=BC,
∴△BOC是等边三角形,∴∠AOC=60°,
∴tan∠AOC=tan60°=
,
故答案为:D.
8.【答案】
D
【解答】解:∵cosB=,
∴∠B=45°,
①若△ABC为钝角三角形,如图1:
在Rt△ADB中,
∵AB=12,
∠B=45°,
∴AD=BD=12,
在Rt△ADC中,
∵AC=13,AD=12,
∴CD=5,
∴BC=BD-CD=12-5=7;
②若△ABC为锐角三角形,如图2:
在Rt△ADB中,
∵AB=12,
∠B=45°,
∴AD=BD=12,
在Rt△ADC中,
∵AC=13,AD=12,
∴CD=5,
∴BC=BD+CD=12+5=17;
综上所述:BC长为7或17.
故答案为:D.
二、填空题
9.【答案】
45°
【解答】∵∠A为锐角,且tanA=1,tan45°=1,
∴∠A=45°.
故答案为:45°.
10.【答案】
<
【解答】解:∵tan30°=
,cos30°=
,
<
,
∴tan30°<cos30°,
故答案为:<.
11.【答案】
70
【解答】解:∵sinα=cos20°,
∴α=90°﹣20°=70°.
故答案为:70.
12.【答案】
【解答】解:∵菱形对角线互相垂直,
∴∠OEA=∠AOB
,
∵∠OAE=∠BAO
,
∴△OAE∽△ABO
,
∴∠AOE=∠ABO
,
∵AO=
AC=2,AB=6,
∴sin∠AOE=sin∠ABO=
=
.
故答案为:
.
13.【答案】
5
【解答】解:作CD⊥AB于D,如图,
在Rt△ACD中,∠A=30°,AC=2
,
∴CD=
AC=
,AD=
CD=3,
在Rt△BCD中,tanB=
,
∴
,
∴BD=2,
∴AB=AD+BD=3+2=5.
14.【答案】
【解答】经过正五边形的中心O作边AB的垂线OC,
则∠BOC=36°,
在直角△OBC中,根据三角函数得到
故答案为:
15.【答案】
【解答】解:过点
作
于点
,过点
作
于点
,
,
,
,
AB=AC=3,
BE=EC=1,BC=2,
又∵
,
∴BD=
,
,
∵
,
∴
,
故答案为:
.
16.【答案】
【解答】解:设右下角顶点为点F,取DF的中点E,连接BE,AE,如图所示.
∵点B为CF的中点,点E为DF的中点,
∴BE∥CD,
∴∠AOD=∠ABE.
在△ABE中,AB=
,AE=2
,BE=
,
∵AB2=AE2+BE2
,
∴∠AEB=90°,
∴cos∠ABE=
=
∴cos∠AOD=
故答案为:
.
三、综合题
17.【答案】
(1)解:
cos45°﹣tan45°
=
×
﹣1
=1﹣1
=0;
(2)解:
sin60°+tan60°﹣2cos230°
=
×
+
﹣2×
=
+
﹣
=
.
18.【答案】
(1)解:如表,
锐角
1
(2)增大;减少;增大
(3);30°
(4)1
(5)30°
(6)45°
【解答】解:(2)由(1)表格可知,随着锐角α逐渐增大,sinα的值逐渐增发,cosα的值逐渐减少,tanα的值逐渐增大.
(3)由(1)表格可知,sin30°=cos60°.
(4)原式=
(5)∵左边=
tan30°=
∴
故答案为:30°
19.【答案】
解:(1)如图①点C即为所求作的点;
(
2
)如图②,点D即为所求作的点|
20.【答案】
解:∵在Rt△ABC中,a=5,c=13,∴AC=12,sinA=
=
,cosA=
=
,
tanA=
=
.
21.【答案】
解:
(海里)
在
中,
(海里)
22.【答案】
(1)解:∵P为屏幕中心,AB=32
∴AP=16
∵EP⊥AB,∠E=18°
∴sin∠E=
=sin18°≈0.
3
∴AE≈53cm
(2)解:过B点作BF⊥AC于F点
∵BF=sin18°·AB≈9.6cm
AF=cos18°·AB≈28.8cm
又∵∠BCD=∠FBC=30°
∴CF=≈5.6cm
∴AC=AF+CF≈34.3cm≈34cm。
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册1.1
锐角三角函数
同步练习
一、单选题(共8题;共24分)
1.已知
为锐角,且
,则
的度数为(???
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
2.在Rt△ABC中,各边都扩大5倍,则锐角A的正切函数值(??
)
A.?不变???????????????????????????????B.?扩大5倍???????????????????????????????C.?缩小5倍???????????????????????????????D.?不能确定
3.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边AC的长是(??
)
?m·sin35°?????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?m·cos35°
(第3题)
(第4题)
4.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论错误的是(?
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
5.若∠A是锐角,且sinA=
,则(?????
)
A.?0?<∠A<30???????????????????B.?30?<∠A<45???????????????????C.?45?<∠A<60???????????????????D.?60?<∠A<90?
6.在Rt△ABC中,∠C=90°,若sinA=
,
则tanB=(??
)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
7.如图,以
为圆心,任意长为半径画弧,与射线
交于点
,再以
为圆心,
长为半径画弧,两弧交于点
画射线
,则
的值为(
??)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
8.在△ABC中,AB=12
,AC=13,cosB=
,则BC的边长为(
??)
A.?7??????????????????????????????????????B.?8??????????????????????????????????????C.?8或17??????????????????????????????????????D.?7或17
二、填空题(共8题;共24分)
9.若∠A为锐角,且tanA=1,则∠A的度数为________.
10.比较大小:tan30°________
cos30°(用“>”或“<”填空)
11.如果α是锐角,且sinα=cos20°,那么α=________度.
12.已知菱形ABCD的边长为6,对角线AC与BD相交于点O
,
OE⊥AB
,
垂足为点E
,
AC=4,那么sin∠AOE=________.
(第12题)
(第13题)
(第16题)
13.如图,在△ABC中,∠A=30°,tanB=
,AC=2
,AB的长________.
14.正五边形的边长与边心距的比值为________.(用含三角比的代数式表示)
15.如果等腰△ABC中,
,
,那么
________.
16.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD=________.
三、综合题(共6题;共52分)
17.??
(1)计算:
cos45°﹣tan45°;
(2)计算:
sin60°+tan60°﹣2cos230°
18.??(1)完成下列表格,并回答下列问题,
锐角
(2)当锐角
逐渐增大时,
的值逐渐________,
的值逐渐________,
的值逐渐________.
(3)________,
________
;
(4)________;
(5)________;
(6)若
,则锐角
________.
19.图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上,按下列要求画出图形.
(
1
)在图①中找到两个格点C,使∠BAC是锐角,且tan∠BAC=
;
(
2
)在图②中找到两个格点D,使∠ADB是锐角,且tan∠ADB=1.
20.如图,在Rt△ABC中,a=5,c=13,求sinA,cosA,tanA.
21.如图,海面上
,
两岛分别位于
岛的正东和正北方向.一艘船从
岛出发以16海里
的速度向正北方向航行2小吋到达
岛,此吋测得
岛在
岛的南偏东
.求
,
两岛之间的距离.(结果精确到0.1海里)(参考数据:
,
,
)
22.在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕点O旋转一定的角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个18°的俯角(即望向屏幕中心P的视线EP与水平线EA的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时(如图2)时,观看屏幕最舒适。此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽AB为32cm。
(1)求眼睛E与显示屏顶端A的水平距离AE.(结果精确到1cm)
(2)求显示屏顶端A与底座C的距离AC。(结果精确到1cm)
(参考数据:sin18°≈0.3,cos18°≈0.9,tan18°≈0.3,
≈1.4,
≈1.7)
答案解析部分
一、单选题
1.【答案】
B
【解答】解:
为锐角,且
,
.
故答案为:
.
2.【答案】
A
【解答】解:因为三角函数值与对应边的比值有关,所以各边的长度都扩大5倍后,锐有A的各三角函数值没有变化.
故答案为:A.
3.【答案】
D
【解答】解:在Rt△ABC中,
AB=m,∠A=35°,
,
∴AC=
,
故答案为:D.
4.【答案】
C
【解答】解:在Rt△ABC中,∠BAC=90°,sinB=
,B符合题意
∵AD⊥BC,∴sinB=
,A符合题意
sinB=sin∠DAC=
,D符合题意
综上,只有C不符合题意
故答案为:C.
5.【答案】
A
【解答】解:∵sin30°=
又∵0<<
∴0°<∠A<30°
故答案为:A.
6.【答案】
C
【解答】解:∵sinA=,
0
∵A+B=90°,
∴sinB=cosA,cosB=sinA,
∴.
故答案为:C.
7.【答案】
D
【解答】解:如图,连结BC,
则由题意可得OC=OB,CB=OB,∴OC=OB=BC,
∴△BOC是等边三角形,∴∠AOC=60°,
∴tan∠AOC=tan60°=
,
故答案为:D.
8.【答案】
D
【解答】解:∵cosB=,
∴∠B=45°,
①若△ABC为钝角三角形,如图1:
在Rt△ADB中,
∵AB=12,
∠B=45°,
∴AD=BD=12,
在Rt△ADC中,
∵AC=13,AD=12,
∴CD=5,
∴BC=BD-CD=12-5=7;
②若△ABC为锐角三角形,如图2:
在Rt△ADB中,
∵AB=12,
∠B=45°,
∴AD=BD=12,
在Rt△ADC中,
∵AC=13,AD=12,
∴CD=5,
∴BC=BD+CD=12+5=17;
综上所述:BC长为7或17.
故答案为:D.
二、填空题
9.【答案】
45°
【解答】∵∠A为锐角,且tanA=1,tan45°=1,
∴∠A=45°.
故答案为:45°.
10.【答案】
<
【解答】解:∵tan30°=
,cos30°=
,
<
,
∴tan30°<cos30°,
故答案为:<.
11.【答案】
70
【解答】解:∵sinα=cos20°,
∴α=90°﹣20°=70°.
故答案为:70.
12.【答案】
【解答】解:∵菱形对角线互相垂直,
∴∠OEA=∠AOB
,
∵∠OAE=∠BAO
,
∴△OAE∽△ABO
,
∴∠AOE=∠ABO
,
∵AO=
AC=2,AB=6,
∴sin∠AOE=sin∠ABO=
=
.
故答案为:
.
13.【答案】
5
【解答】解:作CD⊥AB于D,如图,
在Rt△ACD中,∠A=30°,AC=2
,
∴CD=
AC=
,AD=
CD=3,
在Rt△BCD中,tanB=
,
∴
,
∴BD=2,
∴AB=AD+BD=3+2=5.
14.【答案】
【解答】经过正五边形的中心O作边AB的垂线OC,
则∠BOC=36°,
在直角△OBC中,根据三角函数得到
故答案为:
15.【答案】
【解答】解:过点
作
于点
,过点
作
于点
,
,
,
,
AB=AC=3,
BE=EC=1,BC=2,
又∵
,
∴BD=
,
,
∵
,
∴
,
故答案为:
.
16.【答案】
【解答】解:设右下角顶点为点F,取DF的中点E,连接BE,AE,如图所示.
∵点B为CF的中点,点E为DF的中点,
∴BE∥CD,
∴∠AOD=∠ABE.
在△ABE中,AB=
,AE=2
,BE=
,
∵AB2=AE2+BE2
,
∴∠AEB=90°,
∴cos∠ABE=
=
∴cos∠AOD=
故答案为:
.
三、综合题
17.【答案】
(1)解:
cos45°﹣tan45°
=
×
﹣1
=1﹣1
=0;
(2)解:
sin60°+tan60°﹣2cos230°
=
×
+
﹣2×
=
+
﹣
=
.
18.【答案】
(1)解:如表,
锐角
1
(2)增大;减少;增大
(3);30°
(4)1
(5)30°
(6)45°
【解答】解:(2)由(1)表格可知,随着锐角α逐渐增大,sinα的值逐渐增发,cosα的值逐渐减少,tanα的值逐渐增大.
(3)由(1)表格可知,sin30°=cos60°.
(4)原式=
(5)∵左边=
tan30°=
∴
故答案为:30°
19.【答案】
解:(1)如图①点C即为所求作的点;
(
2
)如图②,点D即为所求作的点|
20.【答案】
解:∵在Rt△ABC中,a=5,c=13,∴AC=12,sinA=
=
,cosA=
=
,
tanA=
=
.
21.【答案】
解:
(海里)
在
中,
(海里)
22.【答案】
(1)解:∵P为屏幕中心,AB=32
∴AP=16
∵EP⊥AB,∠E=18°
∴sin∠E=
=sin18°≈0.
3
∴AE≈53cm
(2)解:过B点作BF⊥AC于F点
∵BF=sin18°·AB≈9.6cm
AF=cos18°·AB≈28.8cm
又∵∠BCD=∠FBC=30°
∴CF=≈5.6cm
∴AC=AF+CF≈34.3cm≈34cm。
21世纪教育网(www.21cnjy.com)
