1.3 解直角三角形 同步练习(含解析)
文档属性
| 名称 | 1.3 解直角三角形 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 487.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册1.3
解直角三角形
同步练习
一、单选题(共6题;共24分)
1.已知在Rt△ABC中,∠C=90°,AB=5,AC=3,则tanA的值(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
2.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)都为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为(?
)
?5m???????????????????????????????????????B.?6m???????????????????????????????????????C.?7m???????????????????????????????????????D.?8m
(第2题)
(第3题)
(第4题)
3.如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是(??
)
A.?tan55°=
??????????B.?tan55°=
??????????C.?sin55°=
??????????D.?cos55°=
4.有一副三角板,含45°的三角板的斜边与含30°的三角板的长直角边相等,如图,将这副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,则AF的长为(??
)
A.?2??????????????????????????????B.?2
﹣2??????????????????????????????C.?4﹣2
??????????????????????????????D.?2
﹣
5.如图,河坝横断面迎水坡AB的坡比为1:
,坝高BC=3m,则AB的长度为(
??)
?6m???????????????????????????????????B.?3
m???????????????????????????????????C.?9m???????????????????????????????????D.?6
m
(第5题)
(第6题)
6.某兴趣小组想测量一座大楼
AB的高度.如图,大楼前有一段斜坡BC
,已知
BC的长为
12
米它的坡度
.在离
C点
40
米的
D处,用测量仪测得大楼顶端
A的仰角为
37度,测角仪DE的高度为
1.5米,求大楼AB
的高度约为(?
)米(
)
A.?39.3?????????????????????????????????????B.?37.8?????????????????????????????????????C.?33.3?????????????????????????????????????D.?25.7
二、填空题(共6题;共24分)
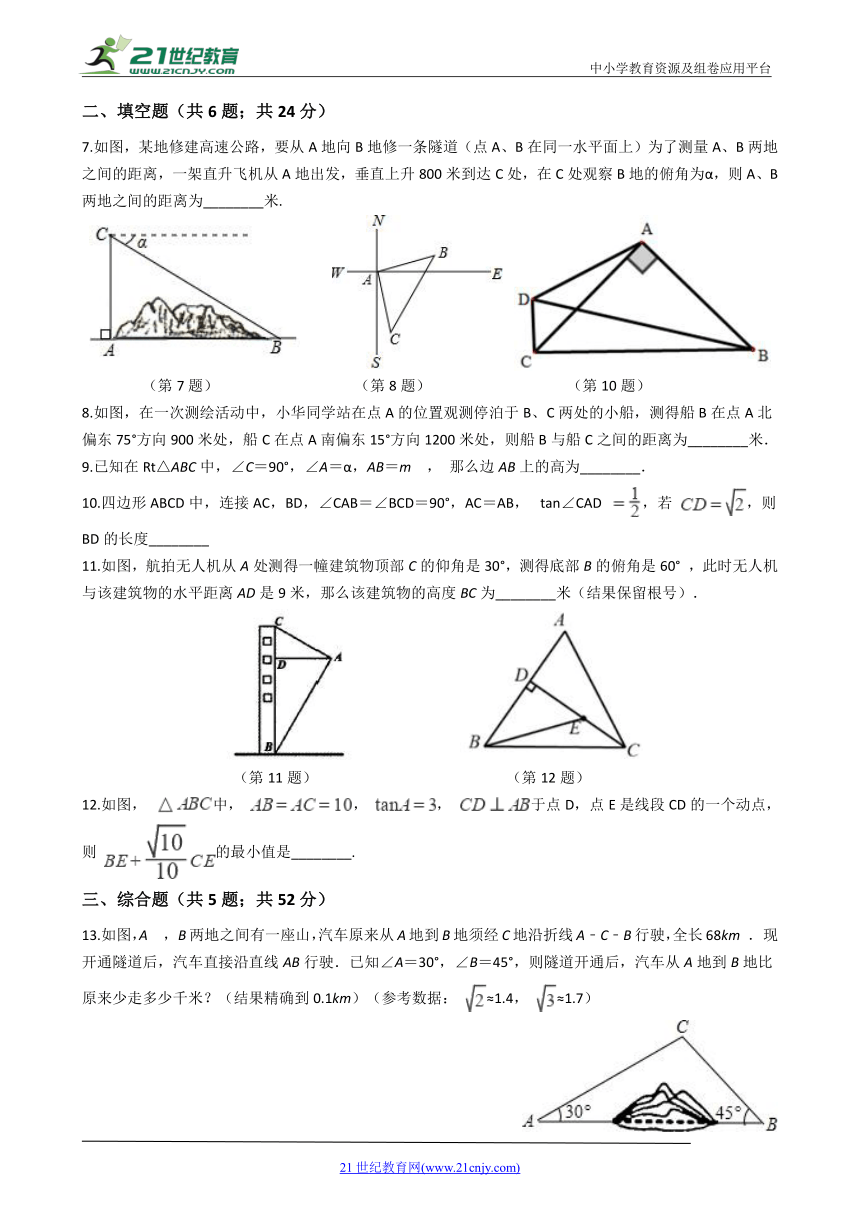
7.如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上)为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为________米.
(第7题)
(第8题)
(第10题)
8.如图,在一次测绘活动中,小华同学站在点A的位置观测停泊于B、C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为________米.
9.已知在Rt△ABC中,∠C=90°,∠A=α,AB=m
,
那么边AB上的高为________.
10.四边形ABCD中,连接AC,BD,∠CAB=∠BCD=90°,AC=AB,?
tan∠CAD
,若
,则BD的长度________
11.如图,航拍无人机从A处测得一幢建筑物顶部C的仰角是30°,测得底部B的俯角是60°
,此时无人机与该建筑物的水平距离AD是9米,那么该建筑物的高度BC为________米(结果保留根号).
(第11题)
(第12题)
12.如图,
中,
,
,
于点D,点E是线段CD的一个动点,则
的最小值是________.
三、综合题(共5题;共52分)
13.如图,A
,
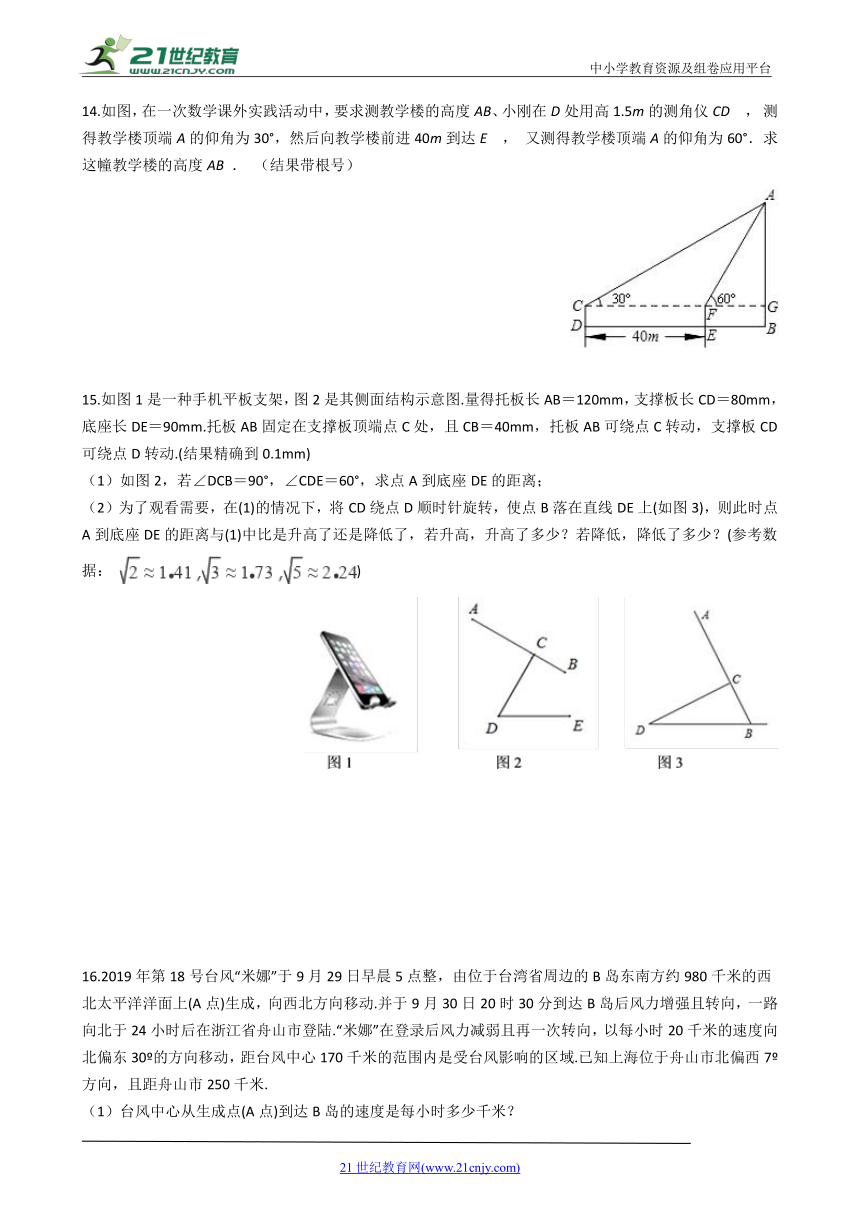
B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,全长68km
.
现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:
≈1.4,
≈1.7)
14.如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD
,
测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E
,
又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB
.
(结果带根号)
15.如图1是一种手机平板支架,图2是其侧面结构示意图.量得托板长AB=120mm,支撑板长CD=80mm,底座长DE=90mm.托板AB固定在支撑板顶端点C处,且CB=40mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果精确到0.1mm)
(1)如图2,若∠DCB=90°,∠CDE=60°,求点A到底座DE的距离;
(2)为了观看需要,在(1)的情况下,将CD绕点D顺时针旋转,使点B落在直线DE上(如图3),则此时点A到底座DE的距离与(1)中比是升高了还是降低了,若升高,升高了多少?若降低,降低了多少?(参考数据:
)
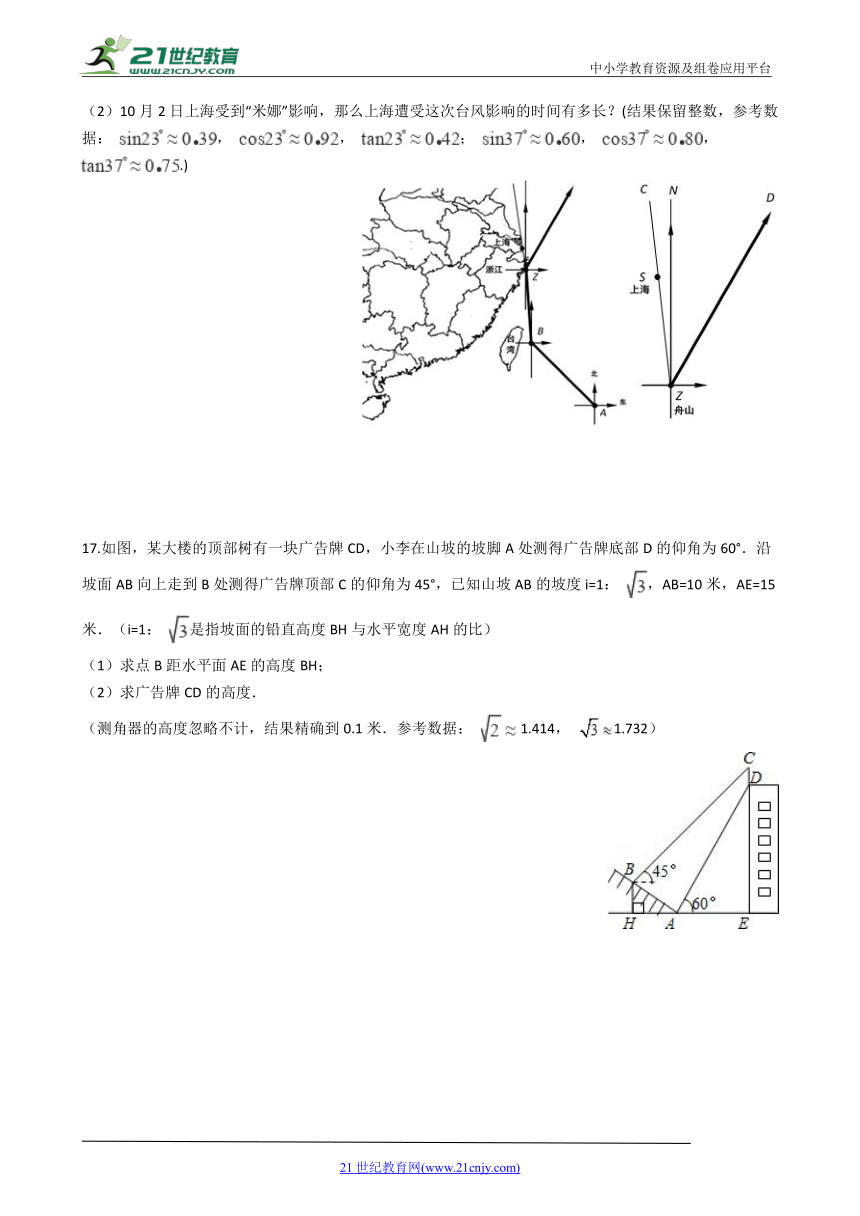
16.2019年第18号台风“米娜”于9月29日早晨5点整,由位于台湾省周边的B岛东南方约980千米的西北太平洋洋面上(A点)生成,向西北方向移动.并于9月30日20时30分到达B岛后风力增强且转向,一路向北于24小时后在浙江省舟山市登陆.“米娜”在登录后风力减弱且再一次转向,以每小时20千米的速度向北偏东30?的方向移动,距台风中心170千米的范围内是受台风影响的区域.已知上海位于舟山市北偏西7?方向,且距舟山市250千米.
(1)台风中心从生成点(A点)到达B岛的速度是每小时多少千米?
(2)10月2日上海受到“米娜”影响,那么上海遭受这次台风影响的时间有多长?(结果保留整数,参考数据:
,
,
;
,
,
.)
17.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
,AB=10米,AE=15米.(i=1:
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:
1.414,
1.732)
答案解析部分
一、单选题
1.【答案】
B
【解答】解:∵∠C=90°,AB=5,AC=3
∴BC=
∴
故答案为:B
2.【答案】
A
【解答】解:如下图:
∵AB的坡度为0.75=,
∴,
即:,
∴AC=3,
∴AB=5,
∴相邻两树间的坡面距离为5
m.
故答案为:A.
3.【答案】
B
【解答】解:∵在Rt△ADE中,DE=6,AE=AB﹣BE=AB﹣CD=x﹣1,∠ADE=55°,
∴sin55°=
,cos55°=
,tan55°=
,
故答案为:B.
4.【答案】
D
【解答】解:在Rt△ABC中,BC=2,∠A=30°,
AC=
=2
,
则EF=AC=2
,
∵∠E=45°,
∴FC=EF?sinE=
,
∴AF=AC﹣FC=2
﹣
,
故答案为:D.
5.【答案】
A
【解答】解:∵迎水坡AB的坡比为1:
,
∴
,即
,
解得,AC=3
,
由勾股定理得,AB
6(m),
故答案为:A.
6.【答案】
C
【解答】解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,
=
,
∴设BF=k,则CF=
k,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=
,
∵DF=DC+CF,
∴DF=40+
,
∵在Rt△AEH中,tan∠AEH=
,
∴AH=tan37°×(40+
)≈37.785(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=37.785-4.5≈33.3.
故答案为:C.
二、填空题
7.【答案】
【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,
∴tanα=
,
∴AB=
=
(米).
故答案为:
.
8.【答案】
1500
【解答】解:∵∠NAB=75°,∠SAC=15°,
∴∠BAC=180°-75°-15°=90°,
在Rt△ABC中,∵AB=900,AC=1200,
∴.
故答案为:1500.
9.【答案】
msinαcosα
【解答】解:如图所示:
根据题意可得:AC=mcosα,BC=msinα,
∴
AC?BC=
mh
,
即h=msinαcosα,
故答案是:msinαcosα.
10.【答案】
【解答】解:过点D作DE⊥AC,交AC于点E
,如图所示:
∵∠CAB=90°,AC=AB
∴△ABC是等腰直角三角形
∴∠ACB
=45°
∵∠BCD=90°
∴∠ACD=45°
∴△DCE为等腰直角三角形
∵
∴DE=CE=1
∵tan∠CAD
∴AE=2
∴AC=AB=3
∴BC=
∴BD=
=
故答案为:
.
11.【答案】
【解答】解:由题意,得∠CAD=30°,∠BAD=60°,
则在Rt△ADC中,
米,
在Rt△ADB中,
米,
∴
米.
故答案为:
.
12.【答案】
【解答】解:如图,作EG⊥AC于G,BH⊥AC于H,
∵CD⊥AB,
∴∠ADC=90°,
∵tanA=
=3,设AD=a,CD=3a,
∵AB=AC=10,
则有:102=a2+9a2
,
∴a2=10,
∴a=
或
(舍),
∴CD=3a=
,
∵AB=AC,CD⊥AB,BH⊥AC,
∴BH=CD=
,
∵∠ECG=∠ACD,∠CGE=∠CDA,
∴sin∠ECG=
=
=
,
∴EG=
EC,
∴BE+
EC=BE+EG,
∴BE+EG≥BH,
∴BE+
EC≥
,
∴BE+
EC的最小值为
.
故答案为:
.
三、综合题
13.【答案】
解:如图,过点C作CD⊥AB,垂足为D,
设CD=x.
在Rt△ACD中,sin∠A=
,AC=
=2x,
在Rt△BCD中,sin∠B=
,BC=
=
x,
∵AC+BC=2x+
x=68,
∴x=
,
在Rt△ACD中,tan∠A=
,AD=
,
在Rt△BCD中,tan∠B=
,BD=
=20,
AB=20
+20≈54,
AC+BC﹣AB=68﹣54=14.0(km).
答:隧道开通后,汽车从A地到B地比原来少走14.0千米.
14.【答案】
解:在Rt△AFG中,tan∠AFG=
,
∴FG=
=
=
.
在Rt△ACG中,tan∠ACG=
,
∴CG=
=
AG.
又CG?FG=40,
即
AG?
=40,
∴AG=20
,
∴AB=20
+1.5.
答:这幢教学楼的高度AB为(20
+1.5)米.
15.【答案】
(1)解:如图1,
过A作
,交ED的延长线于M,过C作
于占F,过C作
,
由题意知,
,
,∠DCB=90°,∠CDE=60°,
在
中,
又∵
∴
∵
∴
∴
∴
在Rt△AFC中,
∵易得四边形MNCF为矩形,
∴
∴
∴点A到底座DE的距离为109.3mm;
(2)解:连接AD,并过A作AQ⊥DB于点Q,如图2,
已知
,
,
在
中,
在
中,
根据
得
,
即
∴
又
,则
,且
答:降低了,降低8.1mm.
16.【答案】
(1)解:由题意得,AB=980千米,台风中心到达B岛的时间是39.5小时.
∴
(千米).
答:台风中心从生成点(A点)到达B岛的速度是每小时25千米.
(2)解:过点S作SH⊥ZD,垂足为点H,
∴∠SHZ=
90°,
∵∠NZD=30°,∠CZN=7°,
∴∠CZD=∠CZN+∠NZD=7°
+
30°=37°.
在Rt△SHZ中,sin∠CZD
=
.
∵∠CZD=37°,SZ=250千米,
∴SH=SZ·sin∠CZD=
(千米).
∵150千米<170千米,
∴设台风中心移动到E处时上海开始遭受台风影响
到F处影响结束.即SE=SF=170(千米).
∵在Rt△SEH中,∠SHE=
90°,
,
∴
.
∴EF=2EH≈160(千米).
∴上海遭受这次台风影响的时间为
(小时).
答:上海遭受这次台风影响的时间为8小时.
17.【答案】
(1)解:过B作BG⊥DE于G,
在Rt△ABF中,i=tan∠BAH=
,∴∠BAH=30°
∴BH=
AB=5(米).
答:点B距水平面AE的高度BH为5米.
(2)解:由(1)得:BH=5,AH=5
,
∴BG=AH+AE=5
+15.
在Rt△BGC中,∠CBG=45°,∴CG=BG=5
+15.
在Rt△ADE中,∠DAE=60°,AE=15,
∴DE=
AE=15
.
∴CD=CG+GE﹣DE=5
+15+5﹣15
=20﹣10
≈2.7(米).
答:宣传牌CD高约2.7米.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册1.3
解直角三角形
同步练习
一、单选题(共6题;共24分)
1.已知在Rt△ABC中,∠C=90°,AB=5,AC=3,则tanA的值(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
2.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)都为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为(?
)
?5m???????????????????????????????????????B.?6m???????????????????????????????????????C.?7m???????????????????????????????????????D.?8m
(第2题)
(第3题)
(第4题)
3.如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点D处测得旗杆顶端A的仰角∠ADE为55°,测角仪CD的高度为1米,其底端C与旗杆底端B之间的距离为6米,设旗杆AB的高度为x米,则下列关系式正确的是(??
)
A.?tan55°=
??????????B.?tan55°=
??????????C.?sin55°=
??????????D.?cos55°=
4.有一副三角板,含45°的三角板的斜边与含30°的三角板的长直角边相等,如图,将这副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,则AF的长为(??
)
A.?2??????????????????????????????B.?2
﹣2??????????????????????????????C.?4﹣2
??????????????????????????????D.?2
﹣
5.如图,河坝横断面迎水坡AB的坡比为1:
,坝高BC=3m,则AB的长度为(
??)
?6m???????????????????????????????????B.?3
m???????????????????????????????????C.?9m???????????????????????????????????D.?6
m
(第5题)
(第6题)
6.某兴趣小组想测量一座大楼
AB的高度.如图,大楼前有一段斜坡BC
,已知
BC的长为
12
米它的坡度
.在离
C点
40
米的
D处,用测量仪测得大楼顶端
A的仰角为
37度,测角仪DE的高度为
1.5米,求大楼AB
的高度约为(?
)米(
)
A.?39.3?????????????????????????????????????B.?37.8?????????????????????????????????????C.?33.3?????????????????????????????????????D.?25.7
二、填空题(共6题;共24分)
7.如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上)为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为________米.
(第7题)
(第8题)
(第10题)
8.如图,在一次测绘活动中,小华同学站在点A的位置观测停泊于B、C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为________米.
9.已知在Rt△ABC中,∠C=90°,∠A=α,AB=m
,
那么边AB上的高为________.
10.四边形ABCD中,连接AC,BD,∠CAB=∠BCD=90°,AC=AB,?
tan∠CAD
,若
,则BD的长度________
11.如图,航拍无人机从A处测得一幢建筑物顶部C的仰角是30°,测得底部B的俯角是60°
,此时无人机与该建筑物的水平距离AD是9米,那么该建筑物的高度BC为________米(结果保留根号).
(第11题)
(第12题)
12.如图,
中,
,
,
于点D,点E是线段CD的一个动点,则
的最小值是________.
三、综合题(共5题;共52分)
13.如图,A
,
B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,全长68km
.
现开通隧道后,汽车直接沿直线AB行驶.已知∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:
≈1.4,
≈1.7)
14.如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD
,
测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E
,
又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB
.
(结果带根号)
15.如图1是一种手机平板支架,图2是其侧面结构示意图.量得托板长AB=120mm,支撑板长CD=80mm,底座长DE=90mm.托板AB固定在支撑板顶端点C处,且CB=40mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果精确到0.1mm)
(1)如图2,若∠DCB=90°,∠CDE=60°,求点A到底座DE的距离;
(2)为了观看需要,在(1)的情况下,将CD绕点D顺时针旋转,使点B落在直线DE上(如图3),则此时点A到底座DE的距离与(1)中比是升高了还是降低了,若升高,升高了多少?若降低,降低了多少?(参考数据:
)
16.2019年第18号台风“米娜”于9月29日早晨5点整,由位于台湾省周边的B岛东南方约980千米的西北太平洋洋面上(A点)生成,向西北方向移动.并于9月30日20时30分到达B岛后风力增强且转向,一路向北于24小时后在浙江省舟山市登陆.“米娜”在登录后风力减弱且再一次转向,以每小时20千米的速度向北偏东30?的方向移动,距台风中心170千米的范围内是受台风影响的区域.已知上海位于舟山市北偏西7?方向,且距舟山市250千米.
(1)台风中心从生成点(A点)到达B岛的速度是每小时多少千米?
(2)10月2日上海受到“米娜”影响,那么上海遭受这次台风影响的时间有多长?(结果保留整数,参考数据:
,
,
;
,
,
.)
17.如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
,AB=10米,AE=15米.(i=1:
是指坡面的铅直高度BH与水平宽度AH的比)
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:
1.414,
1.732)
答案解析部分
一、单选题
1.【答案】
B
【解答】解:∵∠C=90°,AB=5,AC=3
∴BC=
∴
故答案为:B
2.【答案】
A
【解答】解:如下图:
∵AB的坡度为0.75=,
∴,
即:,
∴AC=3,
∴AB=5,
∴相邻两树间的坡面距离为5
m.
故答案为:A.
3.【答案】
B
【解答】解:∵在Rt△ADE中,DE=6,AE=AB﹣BE=AB﹣CD=x﹣1,∠ADE=55°,
∴sin55°=
,cos55°=
,tan55°=
,
故答案为:B.
4.【答案】
D
【解答】解:在Rt△ABC中,BC=2,∠A=30°,
AC=
=2
,
则EF=AC=2
,
∵∠E=45°,
∴FC=EF?sinE=
,
∴AF=AC﹣FC=2
﹣
,
故答案为:D.
5.【答案】
A
【解答】解:∵迎水坡AB的坡比为1:
,
∴
,即
,
解得,AC=3
,
由勾股定理得,AB
6(m),
故答案为:A.
6.【答案】
C
【解答】解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,
=
,
∴设BF=k,则CF=
k,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=
,
∵DF=DC+CF,
∴DF=40+
,
∵在Rt△AEH中,tan∠AEH=
,
∴AH=tan37°×(40+
)≈37.785(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=37.785-4.5≈33.3.
故答案为:C.
二、填空题
7.【答案】
【解答】解:在Rt△ABC中,∵∠CAB=90°,∠B=α,AC=800米,
∴tanα=
,
∴AB=
=
(米).
故答案为:
.
8.【答案】
1500
【解答】解:∵∠NAB=75°,∠SAC=15°,
∴∠BAC=180°-75°-15°=90°,
在Rt△ABC中,∵AB=900,AC=1200,
∴.
故答案为:1500.
9.【答案】
msinαcosα
【解答】解:如图所示:
根据题意可得:AC=mcosα,BC=msinα,
∴
AC?BC=
mh
,
即h=msinαcosα,
故答案是:msinαcosα.
10.【答案】
【解答】解:过点D作DE⊥AC,交AC于点E
,如图所示:
∵∠CAB=90°,AC=AB
∴△ABC是等腰直角三角形
∴∠ACB
=45°
∵∠BCD=90°
∴∠ACD=45°
∴△DCE为等腰直角三角形
∵
∴DE=CE=1
∵tan∠CAD
∴AE=2
∴AC=AB=3
∴BC=
∴BD=
=
故答案为:
.
11.【答案】
【解答】解:由题意,得∠CAD=30°,∠BAD=60°,
则在Rt△ADC中,
米,
在Rt△ADB中,
米,
∴
米.
故答案为:
.
12.【答案】
【解答】解:如图,作EG⊥AC于G,BH⊥AC于H,
∵CD⊥AB,
∴∠ADC=90°,
∵tanA=
=3,设AD=a,CD=3a,
∵AB=AC=10,
则有:102=a2+9a2
,
∴a2=10,
∴a=
或
(舍),
∴CD=3a=
,
∵AB=AC,CD⊥AB,BH⊥AC,
∴BH=CD=
,
∵∠ECG=∠ACD,∠CGE=∠CDA,
∴sin∠ECG=
=
=
,
∴EG=
EC,
∴BE+
EC=BE+EG,
∴BE+EG≥BH,
∴BE+
EC≥
,
∴BE+
EC的最小值为
.
故答案为:
.
三、综合题
13.【答案】
解:如图,过点C作CD⊥AB,垂足为D,
设CD=x.
在Rt△ACD中,sin∠A=
,AC=
=2x,
在Rt△BCD中,sin∠B=
,BC=
=
x,
∵AC+BC=2x+
x=68,
∴x=
,
在Rt△ACD中,tan∠A=
,AD=
,
在Rt△BCD中,tan∠B=
,BD=
=20,
AB=20
+20≈54,
AC+BC﹣AB=68﹣54=14.0(km).
答:隧道开通后,汽车从A地到B地比原来少走14.0千米.
14.【答案】
解:在Rt△AFG中,tan∠AFG=
,
∴FG=
=
=
.
在Rt△ACG中,tan∠ACG=
,
∴CG=
=
AG.
又CG?FG=40,
即
AG?
=40,
∴AG=20
,
∴AB=20
+1.5.
答:这幢教学楼的高度AB为(20
+1.5)米.
15.【答案】
(1)解:如图1,
过A作
,交ED的延长线于M,过C作
于占F,过C作
,
由题意知,
,
,∠DCB=90°,∠CDE=60°,
在
中,
又∵
∴
∵
∴
∴
∴
在Rt△AFC中,
∵易得四边形MNCF为矩形,
∴
∴
∴点A到底座DE的距离为109.3mm;
(2)解:连接AD,并过A作AQ⊥DB于点Q,如图2,
已知
,
,
在
中,
在
中,
根据
得
,
即
∴
又
,则
,且
答:降低了,降低8.1mm.
16.【答案】
(1)解:由题意得,AB=980千米,台风中心到达B岛的时间是39.5小时.
∴
(千米).
答:台风中心从生成点(A点)到达B岛的速度是每小时25千米.
(2)解:过点S作SH⊥ZD,垂足为点H,
∴∠SHZ=
90°,
∵∠NZD=30°,∠CZN=7°,
∴∠CZD=∠CZN+∠NZD=7°
+
30°=37°.
在Rt△SHZ中,sin∠CZD
=
.
∵∠CZD=37°,SZ=250千米,
∴SH=SZ·sin∠CZD=
(千米).
∵150千米<170千米,
∴设台风中心移动到E处时上海开始遭受台风影响
到F处影响结束.即SE=SF=170(千米).
∵在Rt△SEH中,∠SHE=
90°,
,
∴
.
∴EF=2EH≈160(千米).
∴上海遭受这次台风影响的时间为
(小时).
答:上海遭受这次台风影响的时间为8小时.
17.【答案】
(1)解:过B作BG⊥DE于G,
在Rt△ABF中,i=tan∠BAH=
,∴∠BAH=30°
∴BH=
AB=5(米).
答:点B距水平面AE的高度BH为5米.
(2)解:由(1)得:BH=5,AH=5
,
∴BG=AH+AE=5
+15.
在Rt△BGC中,∠CBG=45°,∴CG=BG=5
+15.
在Rt△ADE中,∠DAE=60°,AE=15,
∴DE=
AE=15
.
∴CD=CG+GE﹣DE=5
+15+5﹣15
=20﹣10
≈2.7(米).
答:宣传牌CD高约2.7米.
21世纪教育网(www.21cnjy.com)
