2.2 切线长定理 同步练习(含解析)
文档属性
| 名称 | 2.2 切线长定理 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 454.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册2.2
切线长定理
同步练习
一、单选题(共9题;共27分)
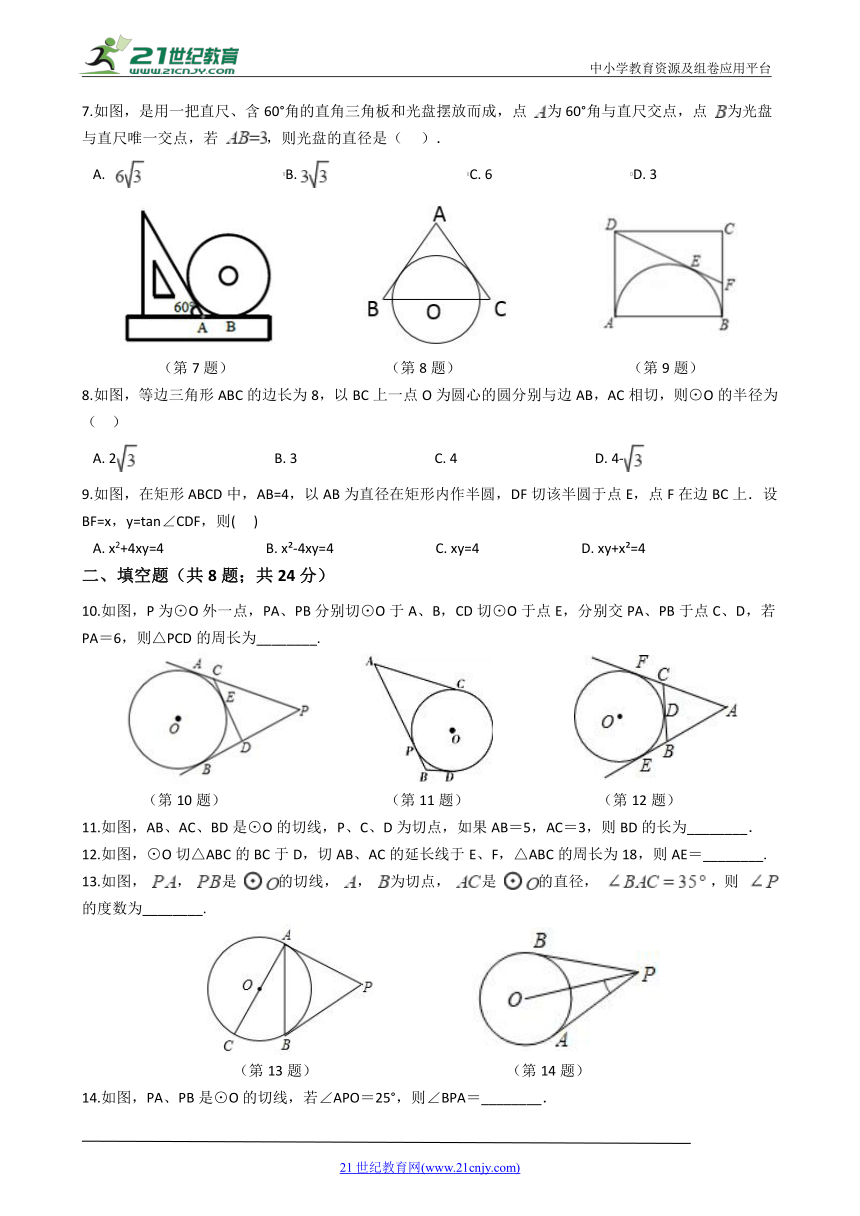
1.如图,P为圆O外一点,
分别切圆O于
两点,若
,则
(??
).
?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
(第1题)
(第2题)
2.如图,PA、PB是⊙O的切线,A、B为切点,若∠P=50°,则∠PAB的度数为(??
)
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?65°???????????????????????????????????????D.?70°
3.如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是(?
)
?1.5?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
(第3题)
(第4题)
4.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
A.?70°???????????????????????????????????????B.?50°???????????????????????????????????????C.?45°???????????????????????????????????????D.?20°
5.如图,AB,BC,CD,DA都是⊙O的切线,已知AD=2,BC=5,则AB+CD的值是(??
)
?14??????????????????????????????????????????B.?12??????????????????????????????????????????C.?9??????????????????????????????????????????D.?7
(第5题)
(第6题)
6.如图,
、
、
是
的切线,
、
、
是切点,
分别交
、
于
、
两点.如
,则
的度数为(???
)
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?75°
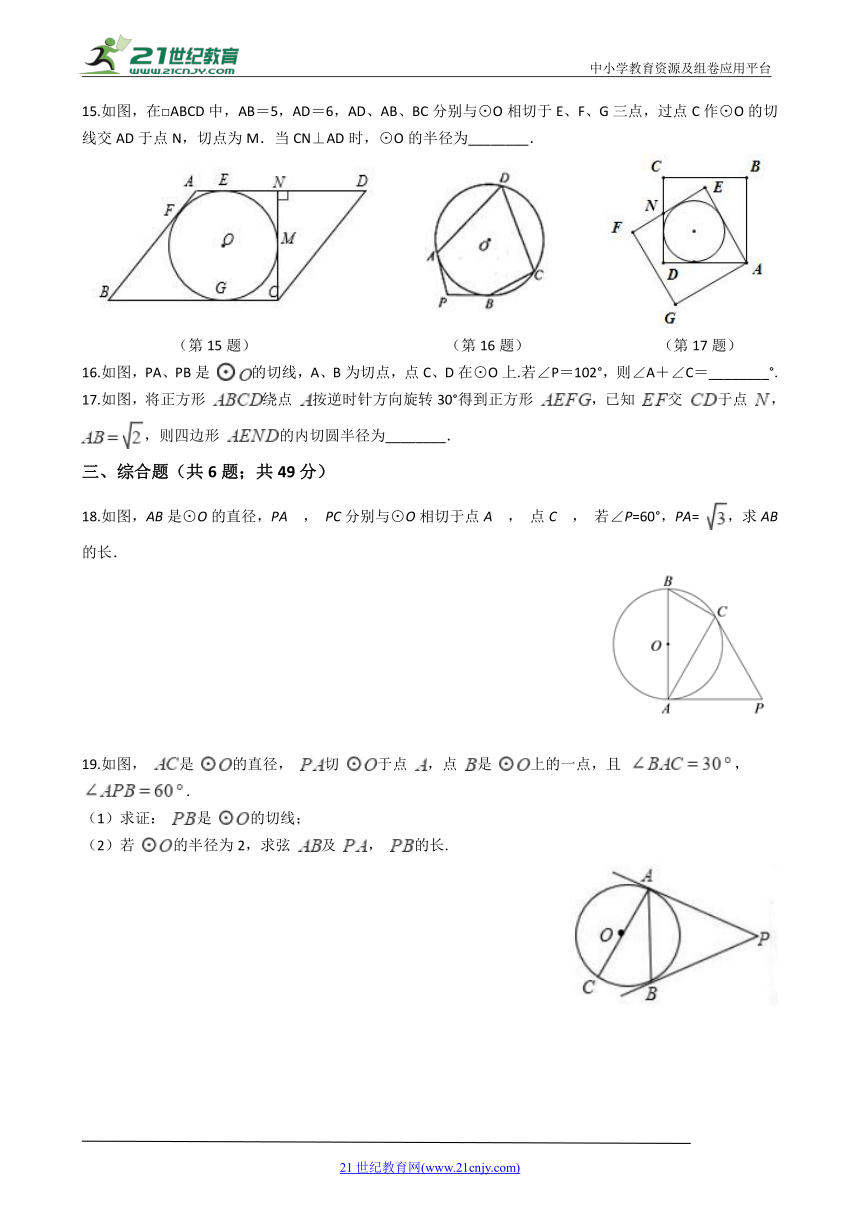
7.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点
为60°角与直尺交点,点
为光盘与直尺唯一交点,若
,则光盘的直径是(???
).
?????????????????????????????????????????B.?????????????????????????????????????????C.?6????????????????????????????????????????D.?3
(第7题)
(第8题)
(第9题)
8.如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为(??
)
A.?2????????????????????????????????????????B.?3????????????????????????????????????????C.?4????????????????????????????????????????D.?4-
9.如图,在矩形ABCD中,AB=4,以AB为直径在矩形内作半圆,DF切该半圆于点E,点F在边BC上.设BF=x,y=tan∠CDF,则(???
)
A.?x2+4xy=4?????????????????????????????B.?x?-4xy=4?????????????????????????????C.?xy=4?????????????????????????????D.?xy+x?=4
二、填空题(共8题;共24分)
10.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=6,则△PCD的周长为________.
(第10题)
(第11题)
(第12题)
11.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为________.
12.如图,⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,△ABC的周长为18,则AE=________.
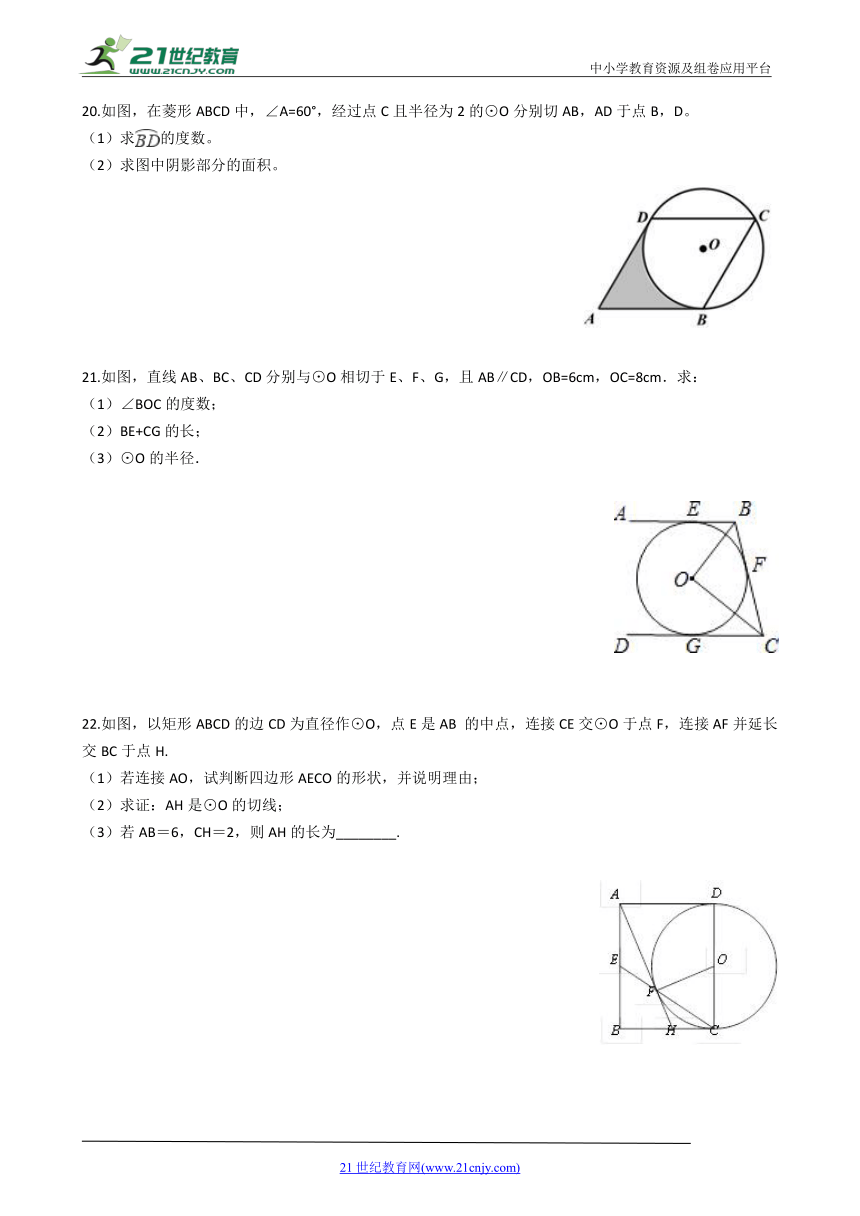
13.如图,
,
是
的切线,
,
为切点,
是
的直径,
,则
的度数为________.
(第13题)
(第14题)
14.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=________.
15.如图,在□ABCD中,AB=5,AD=6,AD、AB、BC分别与⊙O相切于E、F、G三点,过点C作⊙O的切线交AD于点N,切点为M.当CN⊥AD时,⊙O的半径为________.
(第15题)
(第16题)
(第17题)
16.如图,PA、PB是
的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C=________°.
17.如图,将正方形
绕点
按逆时针方向旋转30°得到正方形
,已知
交
于点
,
,则四边形
的内切圆半径为________.
三、综合题(共6题;共49分)
18.如图,AB是⊙O的直径,PA
,
PC分别与⊙O相切于点A
,
点C
,
若∠P=60°,PA=
,求AB的长.
19.如图,
是
的直径,
切
于点
,点
是
上的一点,且
,
.
(1)求证:
是
的切线;
(2)若
的半径为2,求弦
及
,
的长.
20.如图,在菱形ABCD中,∠A=60°,经过点C且半径为2的⊙O分别切AB,AD于点B,D。
(1)求的度数。
(2)求图中阴影部分的面积。
?????
21.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
22.如图,以矩形ABCD的边CD为直径作⊙O,点E是AB
的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.
(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为________.
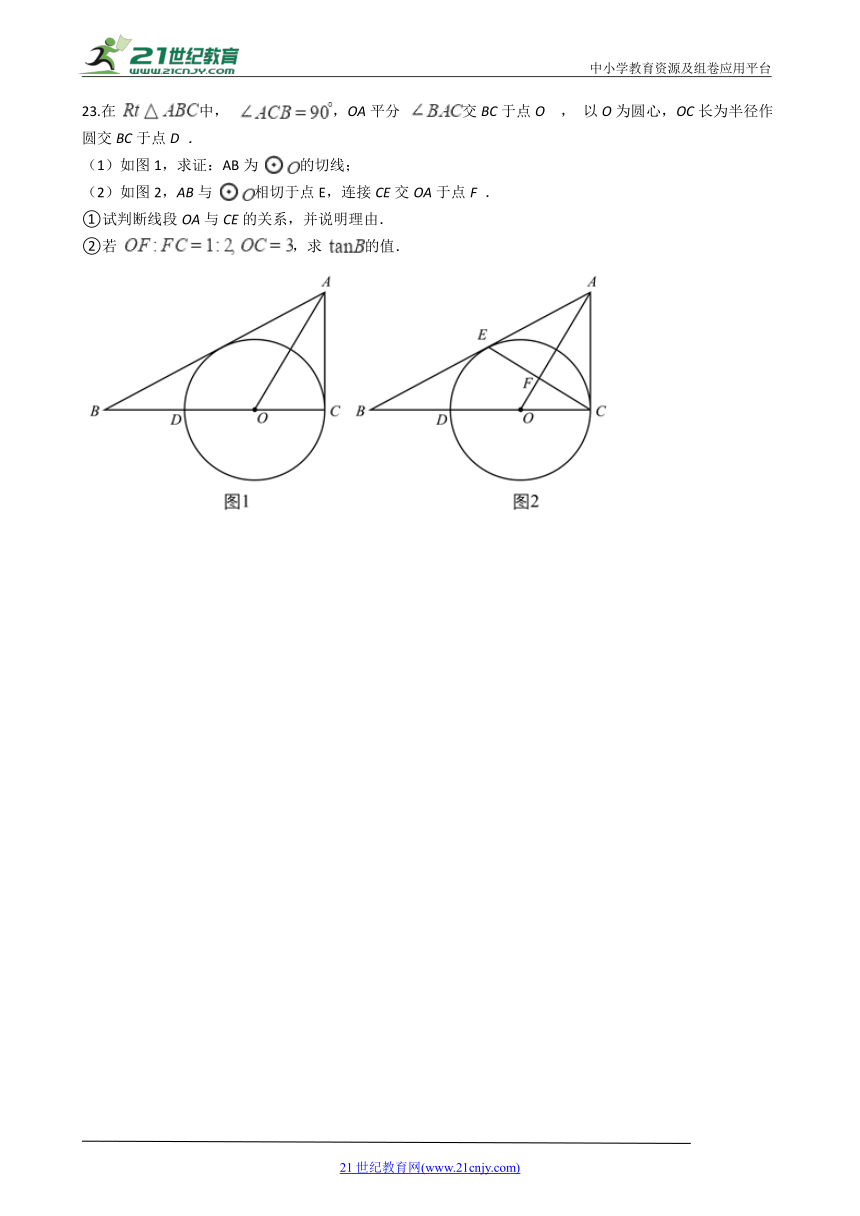
23.在
中,
,OA平分
交BC于点O
,
以O为圆心,OC长为半径作圆交BC于点D
.
(1)如图1,求证:AB为
的切线;
(2)如图2,AB与
相切于点E,连接CE交OA于点F
.
①试判断线段OA与CE的关系,并说明理由.
②若
,求
的值.
答案解析部分
一、单选题
1.【答案】
D
【解答】∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故答案为:D.
2.【答案】
C
【解答】解:∵PA、PB是⊙O的切线,A、B为切点
∴PA=PB
∴∠PAB=∠PBA
∵∠P=50°
∴∠PAB=65°
故答案为:C
3.【答案】
D
【解答】解:连接OD,如图所示
∵PC切⊙O于D
∴∠ODP=90°
∵⊙O的半径为1,PA=AO,AB是⊙O的直径
∴PO=1+1=2,PB=1+1+1=3,OD=1
∴由勾股定理得:PD=
∵BC⊥AB,AB过O
∴BC切⊙O于B
∵PC切⊙O于D
∴CD=BC
设CD=CB=x
在Rt△PBC中,由勾股定理得:PC2=PB2+BC2
即
解得:x=
即BC=
故答案为:D
4.【答案】
B
【解答】解:∵BC是⊙O的切线,OB是⊙O的半径,
∴∠OBC=90°,
∵OA=OB,
∴∠A=∠ABO=20°,
∴∠BOC=40°,
∴∠C=50°.
故选B.
5.【答案】
D
【解答】解:∵AB、BC、CD、DA都是⊙O的切线,
∴可以假设切点分别为E、H、G、F,
∴AF=AE,BE=BH,CH=CG,DG=DF,
∴AD+BC=AF+DF+BH+CH=AE+BE+DG+CG=AB+CD,
∵AD=2,BC=5,
∴AB+CD=AD+BC=7,
故答案为:D.
6.【答案】
C
【解答】解:连接OA、OE、OB,所得图形如下:
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
∴△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=
∠AOB,
∵∠APB=40°,
∴∠AOB=140°,
∴∠COD=70°.
7.【答案】
A
【解答】解:设三角板与圆的切点为C
,
连接OA、OB
,
如下图所示:
由切线长定理知
,
∴
,
在
中,
∴
∴光盘的直径为
,
故答案为:A.
8.【答案】
A
【解答】解:设AB、AC的切点分别为D、E,连结OD、OE,如图,
∵AB、AC与⊙O相切于点D、E,
∴AD=AE,∠ODB=∠OEC=90°,
又∵△ABC是边长为8的等边三角形,
∴AB=AC=BC=8,∠B=60°,
∴BD=CE,
∵OD=OE,
∴△ODB≌△OEC(SAS),
∴OB=OC=
BC=4,
在Rt△ODB中,
∴sin60°=
,
即OD=OBsin60°=4×
=2
,
∴⊙O的半径为2
.
故答案为:A.
9.【答案】
A
【解答】解:∵矩形ABCD,
∴∠C=90°,AB=CD=4,
在Rt△CDF中,
∴CF=4y
∵以AB为直径在矩形内作半圆,DF切该半圆于点E,点F在边BC上,
∴AD=DE=BC=BF+CF=x+4y,EF=BF=x,
∴DF=DE+EF=x+4y+x=2x+4y,
在Rt△CDF中,
CD2+CF2=DF2
∴42+(4y)2=(2x+4y)2
解之:x2+4xy=4
故答案为:A
二、填空题
10.【答案】
12
【解答】解:∵PA、PB切⊙O于A、B,
∴PA=PB=6;
同理,可得:EC=CA,DE=DB;
∴△PDC的周长=PC+CE+DE+DP=PC+AC+PD+DB=PA+PB=2PA=12.
故答案为:12.
11.【答案】
2
【解答】解:根据切线长定理,AP=AC,BP=BD,
所以BP=5-3=2,
所以BD=2.
故答案为:2.
12.【答案】
9
【解答】解:∵⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,
∴BE=BD,DC=CF,AF=AE,
∵△ABC的周长为18,
即AC+BC+AB=AB+DB+DC+AC=AB+BE+AC+CF=18,
∴AE+AF=18,
∴AE=9,
故答案为:9.
13.【答案】
70°
【解答】解:连接OB:
∵PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,
∴∠OAP=∠OBP=90°,
∵∠BAC=35°,OA=OB,
∴∠BAC=∠OBA=35°,
∴∠PAB=∠PBA=55°,
∴∠P=180°?∠PAB?∠PBA=70°,
即∠P的度数是70°,
故答案为:70°.
14.【答案】
50°
【解答】解:∵PA、PB是⊙O的切线,
∴∠BPO=∠APO=25°,
∴∠BPA=50°,
故答案为:50°.
15.【答案】
2或1.5
【解答】解:设半径为r,
∵AD、AB、BC分别与⊙O相切于E、F、G三点,AB=5,AD=6
∴GC=r,BG=BF=6-r,
∴AF=5-(6-r)=r-1=AE
∴ND=6-(r-1)-r=7-2r,
在Rt△NDC中,NC2+ND2=CD2
,
(7-r)2+(2r)2=52
,
解得r=2或1.5.
故答案为:2或1.5.
16.【答案】
219
【解答】解:连接AB,
∵PA、PB是⊙O的切线,
∴PA=PB,
∵∠P=102°,
∴∠PAB=∠PBA=
(180°?102°)=39°,
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=180°+39°=219°,
故答案为:219°.
17.【答案】
【解答】解:作∠DAH与∠AEF的角平分线交于点O,则点O是四边形AEFG内切圆的圆心,过O作OH⊥AE,
则∠OAH=30°,∠AEO=45°,
故EH=OH=
OA,
设EH=x,则AH=
-x,AO=2x,
在Rt△AOH中,
∵AH2+OH2=OA2
,
故(
-x)2+x2=(2x)2
,
解得x=
或x=
(舍去),
∴四边形AEED的内切圆半径为:
.
故答案为:
.
三、综合题
18.【答案】
解:∵PA、PB是⊙D的切线,
∴PA=PC,
∵∠P=60°,
∴△PAC是等边三角形,
∴AC=PA=
,∠PAC=60°,
∵PA是切线,AB是直径,
∴PA⊥AB,∠ACB=90°,
∴∠BAC=30°,
∴AB=
=2.
19.【答案】
(1)证明:连接OB.
∵OA=OB,
∴∠OBA=∠BAC=30°.
∴∠AOB=180°-30°-30°=120°.
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-120°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.?
(2)解:连接OP;
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB=
∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4,
∴PA=
=
=2
.
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2
.
20.【答案】
(1)解:∵在菱形ABCD中,∠A=60°
∴∠C=∠A=60°
∴
的度数为120°.
(2)解:连结OA,OB,OD.
∵⊙O分别切AB,AD于点B,D.
∴OB⊥AB,OD⊥AD,且OA平分∠BAD.
∴∠OAB=∠OAD=30°
∴
∴
.
=
.
21.【答案】
(1)解:连接OF;
根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°
(2)解:由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC=
=10cm,
∴BE+CG=BC=10cm
(3)解:∵OF⊥BC,
∴OF=
=4.8cm
22.【答案】
(1)解:连接AO,四边形AECO是平行四边形.
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E是AB的中点,
∴AE=
AB.
∵CD是⊙O的直径,
∴OC=
CD.∴AE∥OC,AE=OC.
∴四边形AECO为平行四边形.
(2)证明:由(1)得,四边形AECO为平行四边形,
∴AO∥EC
∴∠AOD=∠OCF,∠AOF=∠OFC.
∵OF=OC
∴∠OCF=∠OFC.
∴∠AOD=∠AOF.
∵在△AOD和△AOF中,AO=AO,∠AOD=∠AOF,OD=OF
∴△AOD≌△AOF.
∴∠ADO=∠AFO.
∵四边形ABCD是矩形,
∴∠ADO=90°.
∴∠AFO=90°,即AH⊥OF.
∵点F在⊙O上,
∴AH是⊙O的切线.
(3)
【解答】解:(3)∵HC、FH为圆O的切线,AD、AF是圆O的切线
∴AD=AF,CH=FH=2,
设AD=x,则AF=x,AH=x+2,BH=x-2,
在Rt△ABH中,AH2=AB2+BH2,
即(x+2)2=62+(x-2)2,
解得x=
∴AH=
+2=
.
23.【答案】
(1)证明:如图,过点O作OG⊥AB,垂足为G,
∵OA平分
交BC于点O,
∴OG=OC,
∴点G在
上,
即AB与
相切;
(2)解:①OA垂直平分CE,理由是:
连接OE,
∵AB与
相切于点E,AC与
相切于点C,
∴AE=AC,
∵OE=OC,
∴OA垂直平分CE;
②∵
,
则FC=2OF,在△OCF中,
,
解得:OF=
,则CF=
,
由①得:OA⊥CE,
则∠OCF+∠COF=90°,又∠OCF+∠ACF=90°,
∴∠COF=∠ACF,而∠CFO=∠ACO=90°,
∴△OCF∽△OAC,
∴
,即
,
解得:AC=6,
∵AB与圆O切于点E,
∴∠BEO=90°,AC=AE=6,而∠B=∠B,
∴△BEO∽△BCA,
∴
,设BO=x,BE=y,
则
,
可得:
,
解得:
,即BO=5,BE=4,
∴tanB=
=
.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册2.2
切线长定理
同步练习
一、单选题(共9题;共27分)
1.如图,P为圆O外一点,
分别切圆O于
两点,若
,则
(??
).
?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
(第1题)
(第2题)
2.如图,PA、PB是⊙O的切线,A、B为切点,若∠P=50°,则∠PAB的度数为(??
)
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?65°???????????????????????????????????????D.?70°
3.如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是(?
)
?1.5?????????????????????????????????????????B.?2?????????????????????????????????????????C.??????????????????????????????????????????D.?
(第3题)
(第4题)
4.如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=20°,则∠C的度数是( )
A.?70°???????????????????????????????????????B.?50°???????????????????????????????????????C.?45°???????????????????????????????????????D.?20°
5.如图,AB,BC,CD,DA都是⊙O的切线,已知AD=2,BC=5,则AB+CD的值是(??
)
?14??????????????????????????????????????????B.?12??????????????????????????????????????????C.?9??????????????????????????????????????????D.?7
(第5题)
(第6题)
6.如图,
、
、
是
的切线,
、
、
是切点,
分别交
、
于
、
两点.如
,则
的度数为(???
)
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?75°
7.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点
为60°角与直尺交点,点
为光盘与直尺唯一交点,若
,则光盘的直径是(???
).
?????????????????????????????????????????B.?????????????????????????????????????????C.?6????????????????????????????????????????D.?3
(第7题)
(第8题)
(第9题)
8.如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为(??
)
A.?2????????????????????????????????????????B.?3????????????????????????????????????????C.?4????????????????????????????????????????D.?4-
9.如图,在矩形ABCD中,AB=4,以AB为直径在矩形内作半圆,DF切该半圆于点E,点F在边BC上.设BF=x,y=tan∠CDF,则(???
)
A.?x2+4xy=4?????????????????????????????B.?x?-4xy=4?????????????????????????????C.?xy=4?????????????????????????????D.?xy+x?=4
二、填空题(共8题;共24分)
10.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=6,则△PCD的周长为________.
(第10题)
(第11题)
(第12题)
11.如图,AB、AC、BD是⊙O的切线,P、C、D为切点,如果AB=5,AC=3,则BD的长为________.
12.如图,⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,△ABC的周长为18,则AE=________.
13.如图,
,
是
的切线,
,
为切点,
是
的直径,
,则
的度数为________.
(第13题)
(第14题)
14.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=________.
15.如图,在□ABCD中,AB=5,AD=6,AD、AB、BC分别与⊙O相切于E、F、G三点,过点C作⊙O的切线交AD于点N,切点为M.当CN⊥AD时,⊙O的半径为________.
(第15题)
(第16题)
(第17题)
16.如图,PA、PB是
的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C=________°.
17.如图,将正方形
绕点
按逆时针方向旋转30°得到正方形
,已知
交
于点
,
,则四边形
的内切圆半径为________.
三、综合题(共6题;共49分)
18.如图,AB是⊙O的直径,PA
,
PC分别与⊙O相切于点A
,
点C
,
若∠P=60°,PA=
,求AB的长.
19.如图,
是
的直径,
切
于点
,点
是
上的一点,且
,
.
(1)求证:
是
的切线;
(2)若
的半径为2,求弦
及
,
的长.
20.如图,在菱形ABCD中,∠A=60°,经过点C且半径为2的⊙O分别切AB,AD于点B,D。
(1)求的度数。
(2)求图中阴影部分的面积。
?????
21.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
22.如图,以矩形ABCD的边CD为直径作⊙O,点E是AB
的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.
(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为________.
23.在
中,
,OA平分
交BC于点O
,
以O为圆心,OC长为半径作圆交BC于点D
.
(1)如图1,求证:AB为
的切线;
(2)如图2,AB与
相切于点E,连接CE交OA于点F
.
①试判断线段OA与CE的关系,并说明理由.
②若
,求
的值.
答案解析部分
一、单选题
1.【答案】
D
【解答】∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故答案为:D.
2.【答案】
C
【解答】解:∵PA、PB是⊙O的切线,A、B为切点
∴PA=PB
∴∠PAB=∠PBA
∵∠P=50°
∴∠PAB=65°
故答案为:C
3.【答案】
D
【解答】解:连接OD,如图所示
∵PC切⊙O于D
∴∠ODP=90°
∵⊙O的半径为1,PA=AO,AB是⊙O的直径
∴PO=1+1=2,PB=1+1+1=3,OD=1
∴由勾股定理得:PD=
∵BC⊥AB,AB过O
∴BC切⊙O于B
∵PC切⊙O于D
∴CD=BC
设CD=CB=x
在Rt△PBC中,由勾股定理得:PC2=PB2+BC2
即
解得:x=
即BC=
故答案为:D
4.【答案】
B
【解答】解:∵BC是⊙O的切线,OB是⊙O的半径,
∴∠OBC=90°,
∵OA=OB,
∴∠A=∠ABO=20°,
∴∠BOC=40°,
∴∠C=50°.
故选B.
5.【答案】
D
【解答】解:∵AB、BC、CD、DA都是⊙O的切线,
∴可以假设切点分别为E、H、G、F,
∴AF=AE,BE=BH,CH=CG,DG=DF,
∴AD+BC=AF+DF+BH+CH=AE+BE+DG+CG=AB+CD,
∵AD=2,BC=5,
∴AB+CD=AD+BC=7,
故答案为:D.
6.【答案】
C
【解答】解:连接OA、OE、OB,所得图形如下:
由切线性质得,OA⊥PA,OB⊥PB,OE⊥CD,DB=DE,AC=CE,
∵AO=OE=OB,
∴△AOC≌△EOC(SAS),△EOD≌△BOD(SAS),
∴∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=
∠AOB,
∵∠APB=40°,
∴∠AOB=140°,
∴∠COD=70°.
7.【答案】
A
【解答】解:设三角板与圆的切点为C
,
连接OA、OB
,
如下图所示:
由切线长定理知
,
∴
,
在
中,
∴
∴光盘的直径为
,
故答案为:A.
8.【答案】
A
【解答】解:设AB、AC的切点分别为D、E,连结OD、OE,如图,
∵AB、AC与⊙O相切于点D、E,
∴AD=AE,∠ODB=∠OEC=90°,
又∵△ABC是边长为8的等边三角形,
∴AB=AC=BC=8,∠B=60°,
∴BD=CE,
∵OD=OE,
∴△ODB≌△OEC(SAS),
∴OB=OC=
BC=4,
在Rt△ODB中,
∴sin60°=
,
即OD=OBsin60°=4×
=2
,
∴⊙O的半径为2
.
故答案为:A.
9.【答案】
A
【解答】解:∵矩形ABCD,
∴∠C=90°,AB=CD=4,
在Rt△CDF中,
∴CF=4y
∵以AB为直径在矩形内作半圆,DF切该半圆于点E,点F在边BC上,
∴AD=DE=BC=BF+CF=x+4y,EF=BF=x,
∴DF=DE+EF=x+4y+x=2x+4y,
在Rt△CDF中,
CD2+CF2=DF2
∴42+(4y)2=(2x+4y)2
解之:x2+4xy=4
故答案为:A
二、填空题
10.【答案】
12
【解答】解:∵PA、PB切⊙O于A、B,
∴PA=PB=6;
同理,可得:EC=CA,DE=DB;
∴△PDC的周长=PC+CE+DE+DP=PC+AC+PD+DB=PA+PB=2PA=12.
故答案为:12.
11.【答案】
2
【解答】解:根据切线长定理,AP=AC,BP=BD,
所以BP=5-3=2,
所以BD=2.
故答案为:2.
12.【答案】
9
【解答】解:∵⊙O切△ABC的BC于D,切AB、AC的延长线于E、F,
∴BE=BD,DC=CF,AF=AE,
∵△ABC的周长为18,
即AC+BC+AB=AB+DB+DC+AC=AB+BE+AC+CF=18,
∴AE+AF=18,
∴AE=9,
故答案为:9.
13.【答案】
70°
【解答】解:连接OB:
∵PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,
∴∠OAP=∠OBP=90°,
∵∠BAC=35°,OA=OB,
∴∠BAC=∠OBA=35°,
∴∠PAB=∠PBA=55°,
∴∠P=180°?∠PAB?∠PBA=70°,
即∠P的度数是70°,
故答案为:70°.
14.【答案】
50°
【解答】解:∵PA、PB是⊙O的切线,
∴∠BPO=∠APO=25°,
∴∠BPA=50°,
故答案为:50°.
15.【答案】
2或1.5
【解答】解:设半径为r,
∵AD、AB、BC分别与⊙O相切于E、F、G三点,AB=5,AD=6
∴GC=r,BG=BF=6-r,
∴AF=5-(6-r)=r-1=AE
∴ND=6-(r-1)-r=7-2r,
在Rt△NDC中,NC2+ND2=CD2
,
(7-r)2+(2r)2=52
,
解得r=2或1.5.
故答案为:2或1.5.
16.【答案】
219
【解答】解:连接AB,
∵PA、PB是⊙O的切线,
∴PA=PB,
∵∠P=102°,
∴∠PAB=∠PBA=
(180°?102°)=39°,
∵∠DAB+∠C=180°,
∴∠PAD+∠C=∠PAB+∠DAB+∠C=180°+39°=219°,
故答案为:219°.
17.【答案】
【解答】解:作∠DAH与∠AEF的角平分线交于点O,则点O是四边形AEFG内切圆的圆心,过O作OH⊥AE,
则∠OAH=30°,∠AEO=45°,
故EH=OH=
OA,
设EH=x,则AH=
-x,AO=2x,
在Rt△AOH中,
∵AH2+OH2=OA2
,
故(
-x)2+x2=(2x)2
,
解得x=
或x=
(舍去),
∴四边形AEED的内切圆半径为:
.
故答案为:
.
三、综合题
18.【答案】
解:∵PA、PB是⊙D的切线,
∴PA=PC,
∵∠P=60°,
∴△PAC是等边三角形,
∴AC=PA=
,∠PAC=60°,
∵PA是切线,AB是直径,
∴PA⊥AB,∠ACB=90°,
∴∠BAC=30°,
∴AB=
=2.
19.【答案】
(1)证明:连接OB.
∵OA=OB,
∴∠OBA=∠BAC=30°.
∴∠AOB=180°-30°-30°=120°.
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°.
∵四边形的内角和为360°,
∴∠OBP=360°-90°-60°-120°=90°.
∴OB⊥PB.
又∵点B是⊙O上的一点,
∴PB是⊙O的切线.?
(2)解:连接OP;
∵PA、PB是⊙O的切线,
∴PA=PB,∠OPA=∠OPB=
∠APB=30°.
在Rt△OAP中,∠OAP=90°,∠OPA=30°,
∴OP=2OA=2×2=4,
∴PA=
=
=2
.
∵PA=PB,∠APB=60°,
∴PA=PB=AB=2
.
20.【答案】
(1)解:∵在菱形ABCD中,∠A=60°
∴∠C=∠A=60°
∴
的度数为120°.
(2)解:连结OA,OB,OD.
∵⊙O分别切AB,AD于点B,D.
∴OB⊥AB,OD⊥AD,且OA平分∠BAD.
∴∠OAB=∠OAD=30°
∴
∴
.
=
.
21.【答案】
(1)解:连接OF;
根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°
(2)解:由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC=
=10cm,
∴BE+CG=BC=10cm
(3)解:∵OF⊥BC,
∴OF=
=4.8cm
22.【答案】
(1)解:连接AO,四边形AECO是平行四边形.
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E是AB的中点,
∴AE=
AB.
∵CD是⊙O的直径,
∴OC=
CD.∴AE∥OC,AE=OC.
∴四边形AECO为平行四边形.
(2)证明:由(1)得,四边形AECO为平行四边形,
∴AO∥EC
∴∠AOD=∠OCF,∠AOF=∠OFC.
∵OF=OC
∴∠OCF=∠OFC.
∴∠AOD=∠AOF.
∵在△AOD和△AOF中,AO=AO,∠AOD=∠AOF,OD=OF
∴△AOD≌△AOF.
∴∠ADO=∠AFO.
∵四边形ABCD是矩形,
∴∠ADO=90°.
∴∠AFO=90°,即AH⊥OF.
∵点F在⊙O上,
∴AH是⊙O的切线.
(3)
【解答】解:(3)∵HC、FH为圆O的切线,AD、AF是圆O的切线
∴AD=AF,CH=FH=2,
设AD=x,则AF=x,AH=x+2,BH=x-2,
在Rt△ABH中,AH2=AB2+BH2,
即(x+2)2=62+(x-2)2,
解得x=
∴AH=
+2=
.
23.【答案】
(1)证明:如图,过点O作OG⊥AB,垂足为G,
∵OA平分
交BC于点O,
∴OG=OC,
∴点G在
上,
即AB与
相切;
(2)解:①OA垂直平分CE,理由是:
连接OE,
∵AB与
相切于点E,AC与
相切于点C,
∴AE=AC,
∵OE=OC,
∴OA垂直平分CE;
②∵
,
则FC=2OF,在△OCF中,
,
解得:OF=
,则CF=
,
由①得:OA⊥CE,
则∠OCF+∠COF=90°,又∠OCF+∠ACF=90°,
∴∠COF=∠ACF,而∠CFO=∠ACO=90°,
∴△OCF∽△OAC,
∴
,即
,
解得:AC=6,
∵AB与圆O切于点E,
∴∠BEO=90°,AC=AE=6,而∠B=∠B,
∴△BEO∽△BCA,
∴
,设BO=x,BE=y,
则
,
可得:
,
解得:
,即BO=5,BE=4,
∴tanB=
=
.
21世纪教育网(www.21cnjy.com)
