第二章 直线与圆的位置关系 单元测试(含解析)
文档属性
| 名称 | 第二章 直线与圆的位置关系 单元测试(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 597.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-24 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册第二章直线与圆的位置关系
单元测试
考试时间:120分钟
满分:150分
姓名:__________
班级:__________考号:__________
一、单选题(共10题;共40分)
1.已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是(??
)
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
2.下列说法,正确的是(??
)
A.?等弦所对的圆周角相等????????????????????????????????B.?弦所对的两条弧的中点的连线垂直平分弦,且过圆心
C.?切线垂直于圆的半径???????????????????????????????????D.?平分弦的直径垂直于弦
3.如图所示,已知
为
的直径,直线
为圆的一条切线,在圆周上有一点
,且使得
,连接
,则
的大小为(??
)
?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
(第3题)
(第5题)
4.已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是(??
)
A.?d=3??????????????????????????????????B.?d>3??????????????????????????????????C.?0≤d<3??????????????????????????????????D.?d<3
5.如图,PO是⊙O外一点,PA是⊙O的切线,PO=26cm,PA=24
cm,则⊙O的周长为(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
6.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
?120°????????????????????????????????????B.?125°????????????????????????????????????C.?130°????????????????????????????????????D.?135°
(第6题)
(第7题)
7.如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是(??
)
A.?DO∥AB???????????????????B.?△ADE是等腰三角形???????????????????C.?DE⊥AC???????????????????D.?DE是⊙O的切线
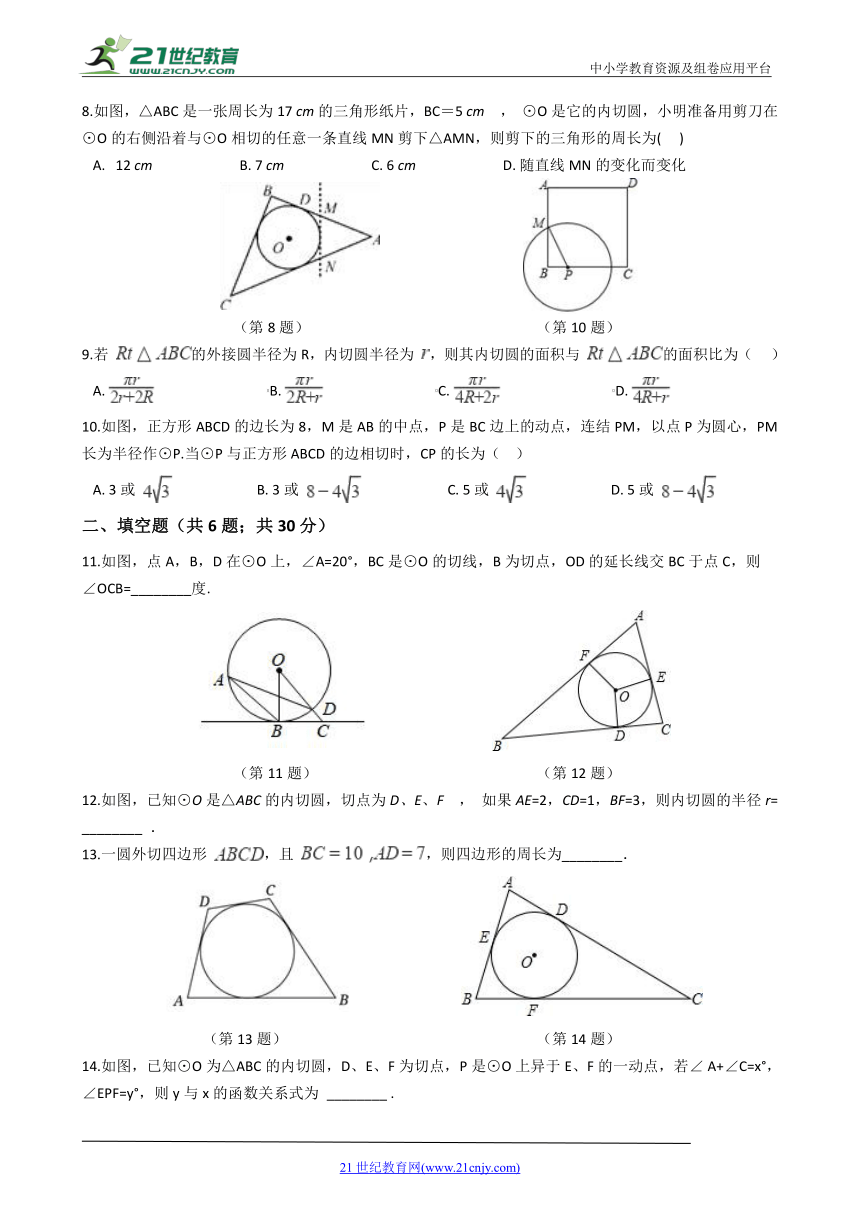
8.如图,△ABC是一张周长为17
cm的三角形纸片,BC=5
cm
,
⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为(???
)
?12
cm?????????????????????????B.?7
cm?????????????????????????C.?6
cm?????????????????????????D.?随直线MN的变化而变化
(第8题)
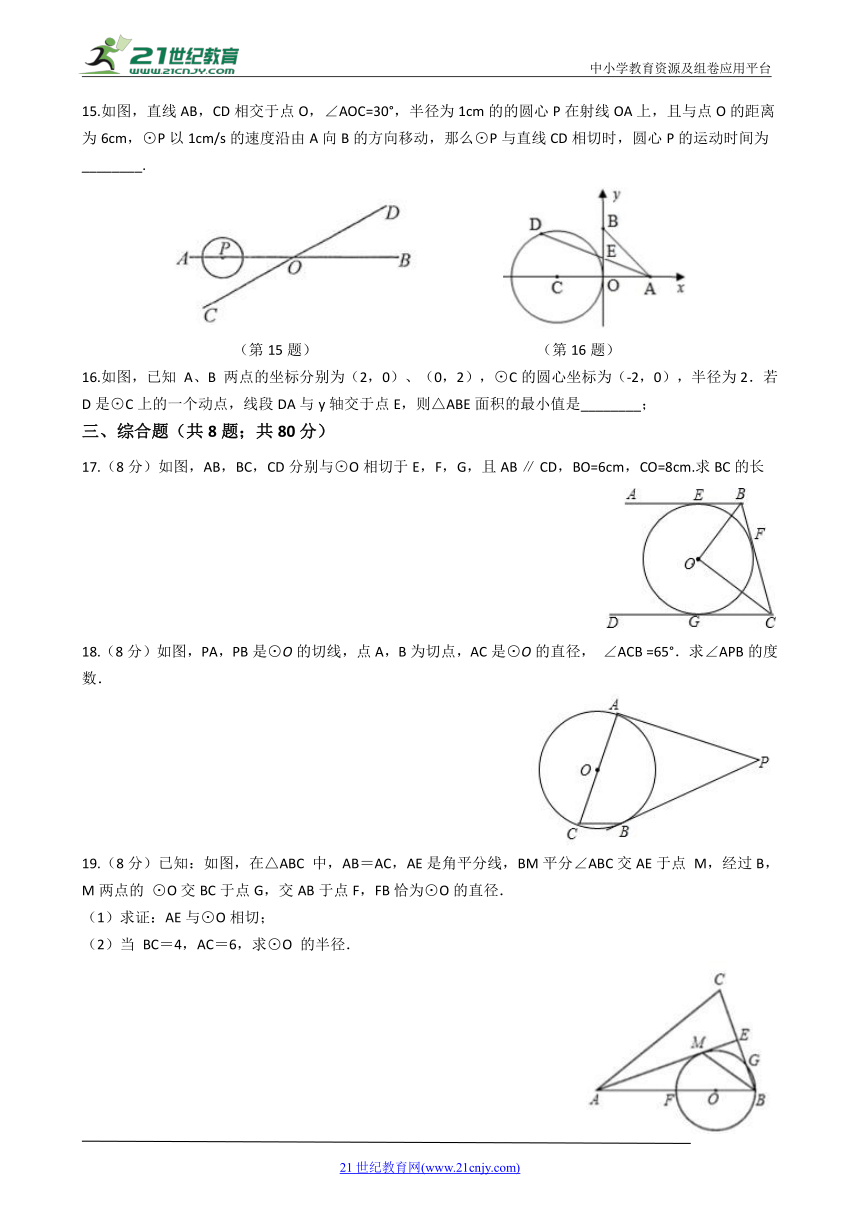
(第10题)
9.若
的外接圆半径为R,内切圆半径为
,则其内切圆的面积与
的面积比为(???
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
10.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,CP的长为(??
)
A.?3或
????????????????????????B.?3或
????????????????????????C.?5或
????????????????????????D.?5或
二、填空题(共6题;共30分)
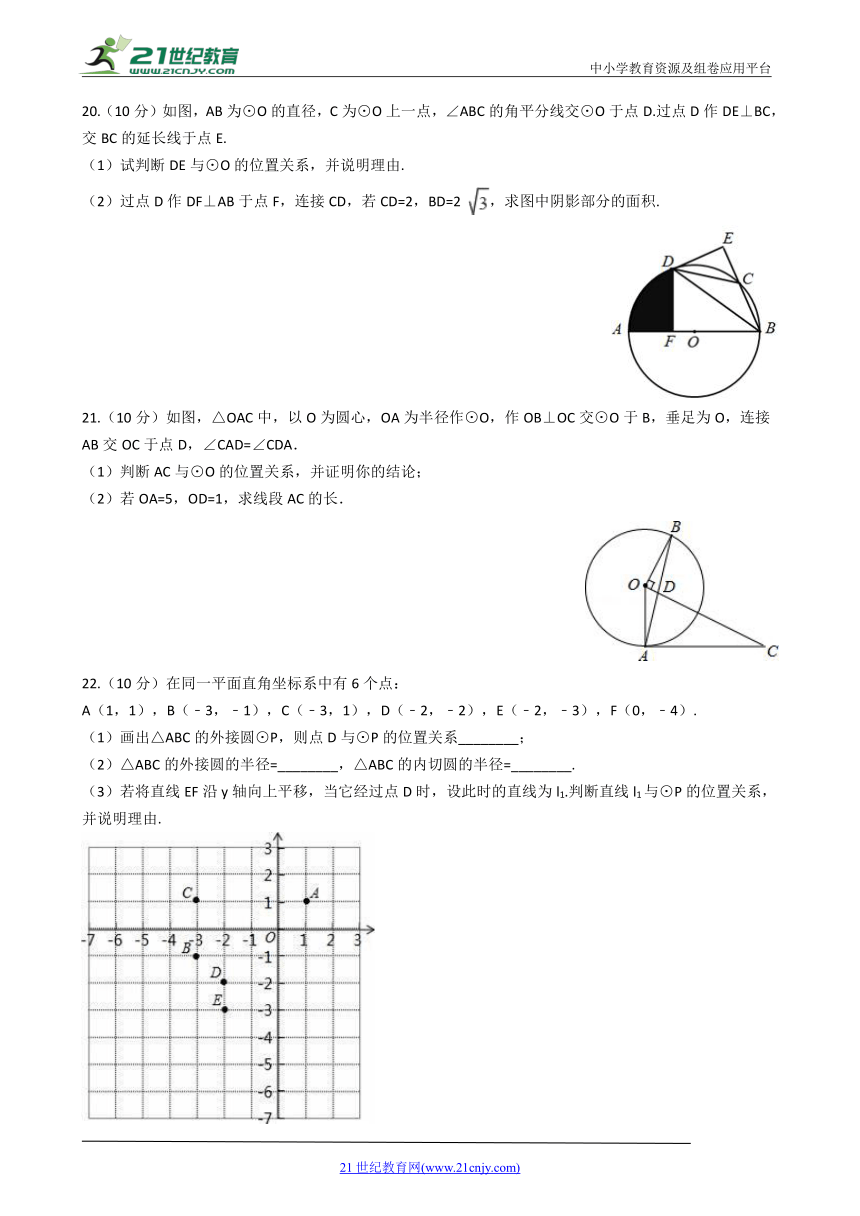
11.如图,点A,B,D在⊙O上,∠A=20°,BC是⊙O的切线,B为切点,OD的延长线交BC于点C,则∠OCB=________度.
(第11题)
(第12题)
12.如图,已知⊙O是△ABC的内切圆,切点为D、E、F
,
如果AE=2,CD=1,BF=3,则内切圆的半径r=
________
.
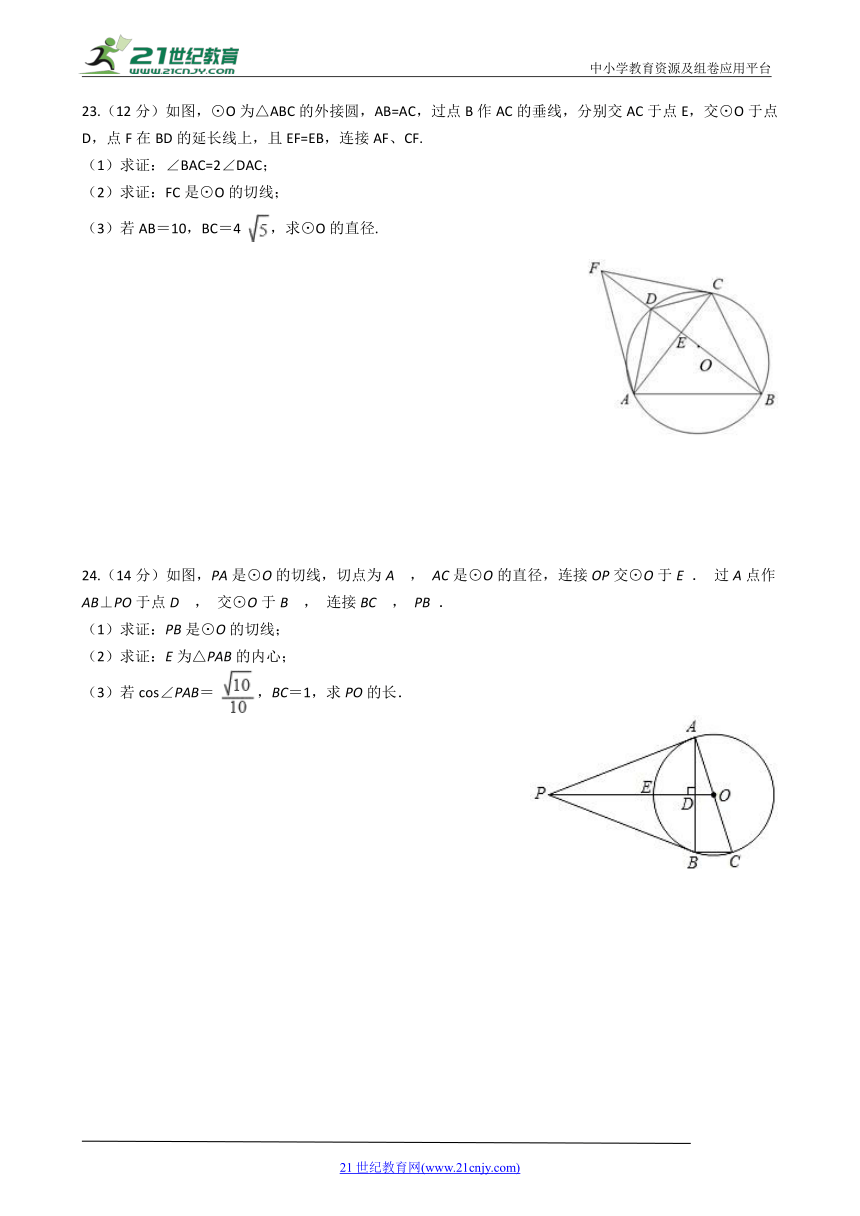
13.一圆外切四边形
,且
,则四边形的周长为________.
(第13题)
(第14题)
14.如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是⊙O上异于E、F的一动点,若∠
A+∠C=x°,∠EPF=y°,则y与x的函数关系式为
________
.
15.如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的的圆心P在射线OA上,且与点O的距离为6cm,⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时,圆心P的运动时间为________.
?
(第15题)
(第16题)
16.如图,已知
A、B
两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-2,0),半径为2.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是________;
三、综合题(共8题;共80分)
17.(8分)如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB
∥
CD,BO=6cm,CO=8cm.求BC的长
18.(8分)如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,
∠ACB
=65°.求∠APB的度数.
19.(8分)已知:如图,在△ABC
中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点
M,经过B,M两点的
⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当
BC=4,AC=6,求⊙O
的半径.
20.(10分)如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的角平分线交⊙O于点D.过点D作DE⊥BC,交BC的延长线于点E.
(1)试判断DE与⊙O的位置关系,并说明理由.
(2)过点D作DF⊥AB于点F,连接CD,若CD=2,BD=2
,求图中阴影部分的面积.
21.(10分)如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
22.(10分)在同一平面直角坐标系中有6个点:
A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(﹣2,﹣3),F(0,﹣4).
(1)画出△ABC的外接圆⊙P,则点D与⊙P的位置关系________;
(2)△ABC的外接圆的半径=________,△ABC的内切圆的半径=________.
(3)若将直线EF沿y轴向上平移,当它经过点D时,设此时的直线为l1.判断直线l1与⊙P的位置关系,并说明理由.
23.(12分)如图,⊙O为△ABC的外接圆,AB=AC,过点B作AC的垂线,分别交AC于点E,交⊙O于点D,点F在BD的延长线上,且EF=EB,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)求证:FC是⊙O的切线;
(3)若AB=10,BC=4
,求⊙O的直径.
24.(14分)如图,PA是⊙O的切线,切点为A
,
AC是⊙O的直径,连接OP交⊙O于E
.
过A点作AB⊥PO于点D
,
交⊙O于B
,
连接BC
,
PB
.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=
,BC=1,求PO的长.
答案解析部分
一、单选题
1.【答案】
C
【解答】解:∵d=6,
r=5,
∴d>r
,
∴
直线AB于⊙O的位置关系是相离;
故答案为:C.
2.【答案】
B
【解答】解:在同圆或等圆中,等弦所对的圆周角相等,故A选项错误;
弦所对的两条弧的中点的连线垂直平分弦,且过圆心,故B选项正确;
切线垂直于过切点的圆的半径,故C选项错误;
平分弦(不是直径)的直径垂直于弦,故D选项错误;
故答案为:B.
3.【答案】
C
【解答】解:如图:连接OB
∵
为
的直径
∴∠ACB=90°
又∵AO=OC
∴OB=
AC=OC
∴OC=OB=BC
∴△COB是等边三角形
∴∠C=60°
∴∠BAC=90°-∠C=30°
又∵直线
为圆的一条切线
∴∠CAP=90°
∴
=∠CAP-∠BAC=60°
故答案为C.
4.【答案】
C
【解答】∵⊙O的半径为3,直线l与⊙O相交,
∴圆心D到直线l的距离d的取值范围是0≤d<3,
故答案为:C.
5.【答案】
C
【解答】解:如图,连接OA,
∵PA是⊙O的切线,
∴OA⊥PA,
即∠PAO=90°,
∴AO=
=10,
∴⊙O的周长为
.
故答案为:C.
6.【答案】
B
【解答】解:∵O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°﹣∠A)=
(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故答案为:B.
7.【答案】
C
【解答】连接OE
∵D为AC中点,O为BC中点
∴OD为△ABC的中位线,
∴DO∥AB,选项A正确;
∵∠COD=∠B,∠DOE=∠OEB,
∵OE=OB,
∴∠OEB=∠B,
∴∠COD=∠DOE,
在△COD和△EOD中,
?,
∴△COD≌△EOD(SAS),
∴∠OED=∠OCD=90°,
∴DE为圆O的切线,选项D正确;
连接EC,∵BC是直径,
∴∠AEC=∠CEB=90°,
在Rt?AEC中,
∵AD=DC,
∴DE=AD,
∴△AED为等腰三角形,选项B正确,
则不一定正确的为DE⊥AC.
故答案为:C.
8.【答案】
B
【解答】设
分别是
的切点,
是一张三角形的纸片,
是它的内切圆,点
是其中的一个切点,
则
故
故答案为:B.
9.【答案】
B
【解答】解:如图,由题意得:
,
由切线长定理可得:
?
设
,
,
而
故答案为:B.
10.【答案】
D
【解答】解:如图1中,当⊙P与直线CD相切时,设PC=PM=x.
在Rt△PBM中,∵PM2=BM2+PB2
,
∴x2=42+(8?x)2
,
∴x=5,
∴CP=5;
如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.
∴PM=PK=CD=2BM,
∴BM=4,PM=8,
在Rt△PBM中,PB=
=
,
∴CP=8-
.
综上所述,CP的长为5或8-
.
二、填空题
11.【答案】
50
【解答】解:∵∠A=20°,
∴∠BOC=40°,
∵BC是⊙O的切线,B为切点,
∴∠OBC=90°,
∴∠OCB=90°-40°=50°.
故答案为:50.
12.【答案】
1
【解答】解:∵⊙O是△ABC的内切圆,切点为D、E、F
,
∴AF=AE
,
EC=CD
,
DB=BF
,
∵AE=2,CD=1,BF=3,
∴AF=2,EC=1,BD=3,
∴AB=BF+AF=3+2=5,BC=BD+DC=4,AC=AE+EC=3,
∴△ABC是直角三角形,
∴内切圆的半径r=
=1,
故答案为1.
13.【答案】
34
【解答】如图,
圆与四边形各边的切点为E、F、G和H
根据切线长定理可得,DE=DF,AF=AG,CE=CH,BG=BH
又BC=BH+HC=10,AD=AF+DF=7
∴ABCD的周长=AD+AB+CD+BC
=AD+DE+CE+BC+AG+BG
=AD+DF+CH+BC+BH+AF
=AD+AD+BC+BC
=2BC+2AD
=34
故答案为34.
14.【答案】
或
【解答】解:连接
、
、
、
,
为
的内切圆,
、
、
为切点,
,
,
,
,
,
有两种情况:①当
在优弧
上时,
,②当
在劣弧
上时,
,
,
即:y与x的函数关系式为:
或
;
故答案为:
或
.
15.【答案】
4或8
【解答】解:如图,
当点P运动到点P1时,过点P1作P1E⊥CD于点E,
∴∠P1EO=90°
∵
∠AOC=30°
,P1E=1
∴P1O=2P1E=2
∴PP1=OP-P1O=6-2=4,
∴圆心P的运动时间为4÷1=4;
当点P运动到点P2时,过点P2作P2E⊥CD于点E,
∴∠P2EO=90°
∵
∠AOC=30°
,P2E=1
∴P2O=2P2E=2
∴PP2=OP+P2O=6+2=8,
∴圆心P的运动时间为8÷1=8;
故答案为:4或8.
16.【答案】
2-
【解答】解:当AD与⊙C相切,且在x轴的上方时,此时BE最小,以BE为底,OA为高,所以△ABE的面积最小,
连接CD,
则CD⊥AD,
∴A、B两点的坐标是(2,0),(0,2),
在Rt△ACD中,CD=2,AC=OC+OA=4,
由勾股定理,得:AD=
,
∴S△ACD=
AD?CD=
×
×2=
,
在△AOE和△ADC中
∵∠OAE=∠DAC,∠EOA=∠CDA
∴△AOE∽△ADC,
∴
,
∴S△AOE=
=
∴S△ABE=S△AOB-S△AOE=
×2×2-
=2-
.
故答案为:2-
.
三、综合题
17.【答案】
解:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=
∠ABC,∠BCO=
∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=
∠ABC+∠DCB=
(∠ABC+∠DCB)=90°.
∴BC=
cm.
18.【答案】
解:连接OB.
?∵OC=OB,
?∴∠OBC=∠OCB,?
???????????????
∵∠ACB=65°,
∴∠OBC=65°,?????
?
?∴∠AOB=2∠OCB=130°,???
?
∵PA,PB是⊙O的切线,点A,B为切点
∴∠OAP=∠OBP
=90°,???
?
?∴∠APB=360°-180°-130°=50°,
19.【答案】
(1)证明:连接OM,
∵
BM平分∠ABC,OM=OB
∴∠OMB=∠OBM=∠CBM
∵
在△ABC
中,AB=AC,AE是角平分线,
∴AE⊥BC
∴∠AEB=90°
∴∠CBM+∠BME=90°
∴∠BME+∠OMB=90°即∠OME=90°,
∴OM⊥AE,OM是半径
∴AE与圆O相切.
(2)解:∵AE是△ABC的角平分线,AC=AB=6,BC=4,
∴BE=AB=2
设圆O的半径为r,则AO=6-r,
∵OM⊥AE,BC⊥AE
∴OM∥BC,
∴△AOM∽△AEB
∴即
解之:r=1.5
∴圆O的半径为1.5.
(2)利用等腰三角形的性质求出BE的长,设圆的半径为r可表示出AO=6-r;再证明△AOM∽△AEB,利用相似三角形的对应边成比例,建立关于r的方程,解方程求出r的值。
20.【答案】
(1)解:DE与⊙O相切,理由如下:
连接DO,
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC的平分线交⊙O于点D,
∴∠EBD=∠DBO,
∴∠EBD=∠ODB,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE与⊙O相切;
(2)解:连接AD,
∵∠ABC的平分线交⊙O于点D,
∴∠EBD=∠DBO,
∴CD=AD=2,
∵AB为直径,
∴∠ADB=90°,
又∵在
中,BD=
,
∴
,
∴OA=OB=OD=2,
∴OA=OD=AD,即
为等边三角形,
∴∠AOD=60°,
∵DF⊥AB,
∴OF=AF=1,
∴在
中,
,
∴
.
21.【答案】
(1)解:
线段AC是⊙O的切线。理由如下:
∵∠CAD=∠CDA(已知),∠BDO=∠CDA(对顶角相等),
∴∠BDO=∠CAD(等量代换)。
又∵OA=OB(⊙O的半径),∴∠B=∠OAB(等边对等角)。
∵OB⊥OC(已知),∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°。
∴线段AC是⊙O的切线。
(2)解:
设AC=x.
∵∠CAD=∠CDA(已知),∴DC=AC=x(等角对等边)。
∵OA=5,OD=1,∴OC=OD+DC=1+x;
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,OC2=AC2+OA2
,
即(1+x)2=x2+52
,
解得x=12。
∴AC=12.
22.【答案】
(1)解:画出△ABC的外接圆⊙P,如图所示,
点在圆上
(2);3-
(3)解:设直线EF解析式为y=kx+b,
把E和F坐标代入得:
,
解得:
,
∴直线EF解析式为
,
由平移性质及题意得:直线l1解析式为
,
即x+2y+6=0,
∵圆心P(0,﹣1)到直线的距离
,
∴直线l1与⊙P相交.
【解答】解:(1)画出△ABC的外接圆⊙P,如图所示,
∵DP=
,
∴点D与⊙P的位置关系是点在圆上;
故答案为:点在圆上;
(2)△ABC的外接圆的半径=
,△ABC的内切圆的半径
;
故答案为:
;3﹣
;
23.【答案】
(1)证明:∵AB=AC
∴∠ABC=∠ACB
∴∠CAB=180°-2∠ACB
∵BD⊥AC
∴∠BEC=90°,∠DBC+∠ACB=90°
∴∠DBC=90°-∠ACB
∵∠DAC=∠DBC=90°-∠ACB
∴2∠DAC=2(90°-∠ACB)=180°-2∠ACB
∴∠CAB=2∠DAC
(2)解:⊙O的直径CG,连结BG,
∵EF=EB,BD⊥AC
∴CF=CB
∴∠CFD=∠CBD,∠CAB=∠CDB=∠CFD+∠FCD=∠CBD+∠FCD
又由(1)可知∠CAB=2∠DAC=2∠CBD
∴∠FCD=∠CBD=∠CFD
∵CG为直径
∴∠CBG=90°
∴∠FCG=∠FCD+∠DCG=∠CBD+∠DBG=90°
∴FC⊥CG
∵CG为直径
∴FC为⊙O的切线
(3)解:∵AC=AB=10,BC=4
∴设
,
,
∴
,
∴AE=6,CE=4,BE=
8
∵∠CGB=∠EAB
∴sin∠CGB=
=sin∠EAB=
∴CG=
24.【答案】
(1)证明:连结OB,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB⊥PO,
∴PO∥BC
∴∠AOP=∠C,∠POB=∠OBC,
OB=OC,
∴∠OBC=∠C,
∴∠AOP=∠POB,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(SAS),
∴∠OBP=∠OAP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OBP=90°,
∴PB是⊙O的切线;
(2)证明:连结AE,
∵PA为⊙O的切线,
∴∠PAE+∠OAE=90°,
∵AD⊥ED,
∴∠EAD+∠AED=90°,
∵OE=OA,
∴∠OAE=∠AED,
∴∠PAE=∠DAE,即EA平分∠PAD,
∵PA、PB为⊙O的切线,
∴PD平分∠APB
∴E为△PAB的内心;
(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,
∴∠PAB=∠C,
∴cos∠C=cos∠PAB=
,
在Rt△ABC中,cos∠C=
=
=
,
∴AC=
,AO=
,
∵△PAO∽△ABC,
∴
,
∴PO=
=
=5.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学浙教版九年级下册第二章直线与圆的位置关系
单元测试
考试时间:120分钟
满分:150分
姓名:__________
班级:__________考号:__________
一、单选题(共10题;共40分)
1.已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是(??
)
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法确定
2.下列说法,正确的是(??
)
A.?等弦所对的圆周角相等????????????????????????????????B.?弦所对的两条弧的中点的连线垂直平分弦,且过圆心
C.?切线垂直于圆的半径???????????????????????????????????D.?平分弦的直径垂直于弦
3.如图所示,已知
为
的直径,直线
为圆的一条切线,在圆周上有一点
,且使得
,连接
,则
的大小为(??
)
?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
(第3题)
(第5题)
4.已知⊙O的半径为3,直线l与⊙O相交,则圆心O到直线l的距离d的取值范围是(??
)
A.?d=3??????????????????????????????????B.?d>3??????????????????????????????????C.?0≤d<3??????????????????????????????????D.?d<3
5.如图,PO是⊙O外一点,PA是⊙O的切线,PO=26cm,PA=24
cm,则⊙O的周长为(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
6.如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
?120°????????????????????????????????????B.?125°????????????????????????????????????C.?130°????????????????????????????????????D.?135°
(第6题)
(第7题)
7.如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是(??
)
A.?DO∥AB???????????????????B.?△ADE是等腰三角形???????????????????C.?DE⊥AC???????????????????D.?DE是⊙O的切线
8.如图,△ABC是一张周长为17
cm的三角形纸片,BC=5
cm
,
⊙O是它的内切圆,小明准备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为(???
)
?12
cm?????????????????????????B.?7
cm?????????????????????????C.?6
cm?????????????????????????D.?随直线MN的变化而变化
(第8题)
(第10题)
9.若
的外接圆半径为R,内切圆半径为
,则其内切圆的面积与
的面积比为(???
)
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
10.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,CP的长为(??
)
A.?3或
????????????????????????B.?3或
????????????????????????C.?5或
????????????????????????D.?5或
二、填空题(共6题;共30分)
11.如图,点A,B,D在⊙O上,∠A=20°,BC是⊙O的切线,B为切点,OD的延长线交BC于点C,则∠OCB=________度.
(第11题)
(第12题)
12.如图,已知⊙O是△ABC的内切圆,切点为D、E、F
,
如果AE=2,CD=1,BF=3,则内切圆的半径r=
________
.
13.一圆外切四边形
,且
,则四边形的周长为________.
(第13题)
(第14题)
14.如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是⊙O上异于E、F的一动点,若∠
A+∠C=x°,∠EPF=y°,则y与x的函数关系式为
________
.
15.如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的的圆心P在射线OA上,且与点O的距离为6cm,⊙P以1cm/s的速度沿由A向B的方向移动,那么⊙P与直线CD相切时,圆心P的运动时间为________.
?
(第15题)
(第16题)
16.如图,已知
A、B
两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-2,0),半径为2.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是________;
三、综合题(共8题;共80分)
17.(8分)如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB
∥
CD,BO=6cm,CO=8cm.求BC的长
18.(8分)如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,
∠ACB
=65°.求∠APB的度数.
19.(8分)已知:如图,在△ABC
中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点
M,经过B,M两点的
⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当
BC=4,AC=6,求⊙O
的半径.
20.(10分)如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的角平分线交⊙O于点D.过点D作DE⊥BC,交BC的延长线于点E.
(1)试判断DE与⊙O的位置关系,并说明理由.
(2)过点D作DF⊥AB于点F,连接CD,若CD=2,BD=2
,求图中阴影部分的面积.
21.(10分)如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
22.(10分)在同一平面直角坐标系中有6个点:
A(1,1),B(﹣3,﹣1),C(﹣3,1),D(﹣2,﹣2),E(﹣2,﹣3),F(0,﹣4).
(1)画出△ABC的外接圆⊙P,则点D与⊙P的位置关系________;
(2)△ABC的外接圆的半径=________,△ABC的内切圆的半径=________.
(3)若将直线EF沿y轴向上平移,当它经过点D时,设此时的直线为l1.判断直线l1与⊙P的位置关系,并说明理由.
23.(12分)如图,⊙O为△ABC的外接圆,AB=AC,过点B作AC的垂线,分别交AC于点E,交⊙O于点D,点F在BD的延长线上,且EF=EB,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)求证:FC是⊙O的切线;
(3)若AB=10,BC=4
,求⊙O的直径.
24.(14分)如图,PA是⊙O的切线,切点为A
,
AC是⊙O的直径,连接OP交⊙O于E
.
过A点作AB⊥PO于点D
,
交⊙O于B
,
连接BC
,
PB
.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=
,BC=1,求PO的长.
答案解析部分
一、单选题
1.【答案】
C
【解答】解:∵d=6,
r=5,
∴d>r
,
∴
直线AB于⊙O的位置关系是相离;
故答案为:C.
2.【答案】
B
【解答】解:在同圆或等圆中,等弦所对的圆周角相等,故A选项错误;
弦所对的两条弧的中点的连线垂直平分弦,且过圆心,故B选项正确;
切线垂直于过切点的圆的半径,故C选项错误;
平分弦(不是直径)的直径垂直于弦,故D选项错误;
故答案为:B.
3.【答案】
C
【解答】解:如图:连接OB
∵
为
的直径
∴∠ACB=90°
又∵AO=OC
∴OB=
AC=OC
∴OC=OB=BC
∴△COB是等边三角形
∴∠C=60°
∴∠BAC=90°-∠C=30°
又∵直线
为圆的一条切线
∴∠CAP=90°
∴
=∠CAP-∠BAC=60°
故答案为C.
4.【答案】
C
【解答】∵⊙O的半径为3,直线l与⊙O相交,
∴圆心D到直线l的距离d的取值范围是0≤d<3,
故答案为:C.
5.【答案】
C
【解答】解:如图,连接OA,
∵PA是⊙O的切线,
∴OA⊥PA,
即∠PAO=90°,
∴AO=
=10,
∴⊙O的周长为
.
故答案为:C.
6.【答案】
B
【解答】解:∵O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
(180°﹣∠A)=
(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故答案为:B.
7.【答案】
C
【解答】连接OE
∵D为AC中点,O为BC中点
∴OD为△ABC的中位线,
∴DO∥AB,选项A正确;
∵∠COD=∠B,∠DOE=∠OEB,
∵OE=OB,
∴∠OEB=∠B,
∴∠COD=∠DOE,
在△COD和△EOD中,
?,
∴△COD≌△EOD(SAS),
∴∠OED=∠OCD=90°,
∴DE为圆O的切线,选项D正确;
连接EC,∵BC是直径,
∴∠AEC=∠CEB=90°,
在Rt?AEC中,
∵AD=DC,
∴DE=AD,
∴△AED为等腰三角形,选项B正确,
则不一定正确的为DE⊥AC.
故答案为:C.
8.【答案】
B
【解答】设
分别是
的切点,
是一张三角形的纸片,
是它的内切圆,点
是其中的一个切点,
则
故
故答案为:B.
9.【答案】
B
【解答】解:如图,由题意得:
,
由切线长定理可得:
?
设
,
,
而
故答案为:B.
10.【答案】
D
【解答】解:如图1中,当⊙P与直线CD相切时,设PC=PM=x.
在Rt△PBM中,∵PM2=BM2+PB2
,
∴x2=42+(8?x)2
,
∴x=5,
∴CP=5;
如图2中当⊙P与直线AD相切时.设切点为K,连接PK,则PK⊥AD,四边形PKDC是矩形.
∴PM=PK=CD=2BM,
∴BM=4,PM=8,
在Rt△PBM中,PB=
=
,
∴CP=8-
.
综上所述,CP的长为5或8-
.
二、填空题
11.【答案】
50
【解答】解:∵∠A=20°,
∴∠BOC=40°,
∵BC是⊙O的切线,B为切点,
∴∠OBC=90°,
∴∠OCB=90°-40°=50°.
故答案为:50.
12.【答案】
1
【解答】解:∵⊙O是△ABC的内切圆,切点为D、E、F
,
∴AF=AE
,
EC=CD
,
DB=BF
,
∵AE=2,CD=1,BF=3,
∴AF=2,EC=1,BD=3,
∴AB=BF+AF=3+2=5,BC=BD+DC=4,AC=AE+EC=3,
∴△ABC是直角三角形,
∴内切圆的半径r=
=1,
故答案为1.
13.【答案】
34
【解答】如图,
圆与四边形各边的切点为E、F、G和H
根据切线长定理可得,DE=DF,AF=AG,CE=CH,BG=BH
又BC=BH+HC=10,AD=AF+DF=7
∴ABCD的周长=AD+AB+CD+BC
=AD+DE+CE+BC+AG+BG
=AD+DF+CH+BC+BH+AF
=AD+AD+BC+BC
=2BC+2AD
=34
故答案为34.
14.【答案】
或
【解答】解:连接
、
、
、
,
为
的内切圆,
、
、
为切点,
,
,
,
,
,
有两种情况:①当
在优弧
上时,
,②当
在劣弧
上时,
,
,
即:y与x的函数关系式为:
或
;
故答案为:
或
.
15.【答案】
4或8
【解答】解:如图,
当点P运动到点P1时,过点P1作P1E⊥CD于点E,
∴∠P1EO=90°
∵
∠AOC=30°
,P1E=1
∴P1O=2P1E=2
∴PP1=OP-P1O=6-2=4,
∴圆心P的运动时间为4÷1=4;
当点P运动到点P2时,过点P2作P2E⊥CD于点E,
∴∠P2EO=90°
∵
∠AOC=30°
,P2E=1
∴P2O=2P2E=2
∴PP2=OP+P2O=6+2=8,
∴圆心P的运动时间为8÷1=8;
故答案为:4或8.
16.【答案】
2-
【解答】解:当AD与⊙C相切,且在x轴的上方时,此时BE最小,以BE为底,OA为高,所以△ABE的面积最小,
连接CD,
则CD⊥AD,
∴A、B两点的坐标是(2,0),(0,2),
在Rt△ACD中,CD=2,AC=OC+OA=4,
由勾股定理,得:AD=
,
∴S△ACD=
AD?CD=
×
×2=
,
在△AOE和△ADC中
∵∠OAE=∠DAC,∠EOA=∠CDA
∴△AOE∽△ADC,
∴
,
∴S△AOE=
=
∴S△ABE=S△AOB-S△AOE=
×2×2-
=2-
.
故答案为:2-
.
三、综合题
17.【答案】
解:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=
∠ABC,∠BCO=
∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=
∠ABC+∠DCB=
(∠ABC+∠DCB)=90°.
∴BC=
cm.
18.【答案】
解:连接OB.
?∵OC=OB,
?∴∠OBC=∠OCB,?
???????????????
∵∠ACB=65°,
∴∠OBC=65°,?????
?
?∴∠AOB=2∠OCB=130°,???
?
∵PA,PB是⊙O的切线,点A,B为切点
∴∠OAP=∠OBP
=90°,???
?
?∴∠APB=360°-180°-130°=50°,
19.【答案】
(1)证明:连接OM,
∵
BM平分∠ABC,OM=OB
∴∠OMB=∠OBM=∠CBM
∵
在△ABC
中,AB=AC,AE是角平分线,
∴AE⊥BC
∴∠AEB=90°
∴∠CBM+∠BME=90°
∴∠BME+∠OMB=90°即∠OME=90°,
∴OM⊥AE,OM是半径
∴AE与圆O相切.
(2)解:∵AE是△ABC的角平分线,AC=AB=6,BC=4,
∴BE=AB=2
设圆O的半径为r,则AO=6-r,
∵OM⊥AE,BC⊥AE
∴OM∥BC,
∴△AOM∽△AEB
∴即
解之:r=1.5
∴圆O的半径为1.5.
(2)利用等腰三角形的性质求出BE的长,设圆的半径为r可表示出AO=6-r;再证明△AOM∽△AEB,利用相似三角形的对应边成比例,建立关于r的方程,解方程求出r的值。
20.【答案】
(1)解:DE与⊙O相切,理由如下:
连接DO,
∵DO=BO,
∴∠ODB=∠OBD,
∵∠ABC的平分线交⊙O于点D,
∴∠EBD=∠DBO,
∴∠EBD=∠ODB,
∴DO∥BE,
∵DE⊥BC,
∴∠DEB=∠EDO=90°,
∴DE与⊙O相切;
(2)解:连接AD,
∵∠ABC的平分线交⊙O于点D,
∴∠EBD=∠DBO,
∴CD=AD=2,
∵AB为直径,
∴∠ADB=90°,
又∵在
中,BD=
,
∴
,
∴OA=OB=OD=2,
∴OA=OD=AD,即
为等边三角形,
∴∠AOD=60°,
∵DF⊥AB,
∴OF=AF=1,
∴在
中,
,
∴
.
21.【答案】
(1)解:
线段AC是⊙O的切线。理由如下:
∵∠CAD=∠CDA(已知),∠BDO=∠CDA(对顶角相等),
∴∠BDO=∠CAD(等量代换)。
又∵OA=OB(⊙O的半径),∴∠B=∠OAB(等边对等角)。
∵OB⊥OC(已知),∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°。
∴线段AC是⊙O的切线。
(2)解:
设AC=x.
∵∠CAD=∠CDA(已知),∴DC=AC=x(等角对等边)。
∵OA=5,OD=1,∴OC=OD+DC=1+x;
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,OC2=AC2+OA2
,
即(1+x)2=x2+52
,
解得x=12。
∴AC=12.
22.【答案】
(1)解:画出△ABC的外接圆⊙P,如图所示,
点在圆上
(2);3-
(3)解:设直线EF解析式为y=kx+b,
把E和F坐标代入得:
,
解得:
,
∴直线EF解析式为
,
由平移性质及题意得:直线l1解析式为
,
即x+2y+6=0,
∵圆心P(0,﹣1)到直线的距离
,
∴直线l1与⊙P相交.
【解答】解:(1)画出△ABC的外接圆⊙P,如图所示,
∵DP=
,
∴点D与⊙P的位置关系是点在圆上;
故答案为:点在圆上;
(2)△ABC的外接圆的半径=
,△ABC的内切圆的半径
;
故答案为:
;3﹣
;
23.【答案】
(1)证明:∵AB=AC
∴∠ABC=∠ACB
∴∠CAB=180°-2∠ACB
∵BD⊥AC
∴∠BEC=90°,∠DBC+∠ACB=90°
∴∠DBC=90°-∠ACB
∵∠DAC=∠DBC=90°-∠ACB
∴2∠DAC=2(90°-∠ACB)=180°-2∠ACB
∴∠CAB=2∠DAC
(2)解:⊙O的直径CG,连结BG,
∵EF=EB,BD⊥AC
∴CF=CB
∴∠CFD=∠CBD,∠CAB=∠CDB=∠CFD+∠FCD=∠CBD+∠FCD
又由(1)可知∠CAB=2∠DAC=2∠CBD
∴∠FCD=∠CBD=∠CFD
∵CG为直径
∴∠CBG=90°
∴∠FCG=∠FCD+∠DCG=∠CBD+∠DBG=90°
∴FC⊥CG
∵CG为直径
∴FC为⊙O的切线
(3)解:∵AC=AB=10,BC=4
∴设
,
,
∴
,
∴AE=6,CE=4,BE=
8
∵∠CGB=∠EAB
∴sin∠CGB=
=sin∠EAB=
∴CG=
24.【答案】
(1)证明:连结OB,
∵AC为⊙O的直径,
∴∠ABC=90°,
∵AB⊥PO,
∴PO∥BC
∴∠AOP=∠C,∠POB=∠OBC,
OB=OC,
∴∠OBC=∠C,
∴∠AOP=∠POB,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(SAS),
∴∠OBP=∠OAP,
∵PA为⊙O的切线,
∴∠OAP=90°,
∴∠OBP=90°,
∴PB是⊙O的切线;
(2)证明:连结AE,
∵PA为⊙O的切线,
∴∠PAE+∠OAE=90°,
∵AD⊥ED,
∴∠EAD+∠AED=90°,
∵OE=OA,
∴∠OAE=∠AED,
∴∠PAE=∠DAE,即EA平分∠PAD,
∵PA、PB为⊙O的切线,
∴PD平分∠APB
∴E为△PAB的内心;
(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,
∴∠PAB=∠C,
∴cos∠C=cos∠PAB=
,
在Rt△ABC中,cos∠C=
=
=
,
∴AC=
,AO=
,
∵△PAO∽△ABC,
∴
,
∴PO=
=
=5.
21世纪教育网(www.21cnjy.com)
