浙教版 信息技术 必修1 2.3 用算法解决问题的过程 课件(共19张PPT)
文档属性
| 名称 | 浙教版 信息技术 必修1 2.3 用算法解决问题的过程 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览






文档简介
第2章 算法与问题解决
浙教版(2019版) 信息技术(高中)
必修1 数据与计算
2.3 用算法解决问题的过程
学习目标
1
2
3
抽象与建模
设计算法
描述算法
1
2
重点难点
重点:抽象与建模,设计算法。
难点:抽象与建模,设计算法。
课堂导入
用计算机解决问题时,由于实际问题情境的复杂性,需要对实际问题进行抽象与建模,再根据建立的计算模型设计算法,并将算法用合适的方式加以准确描述。
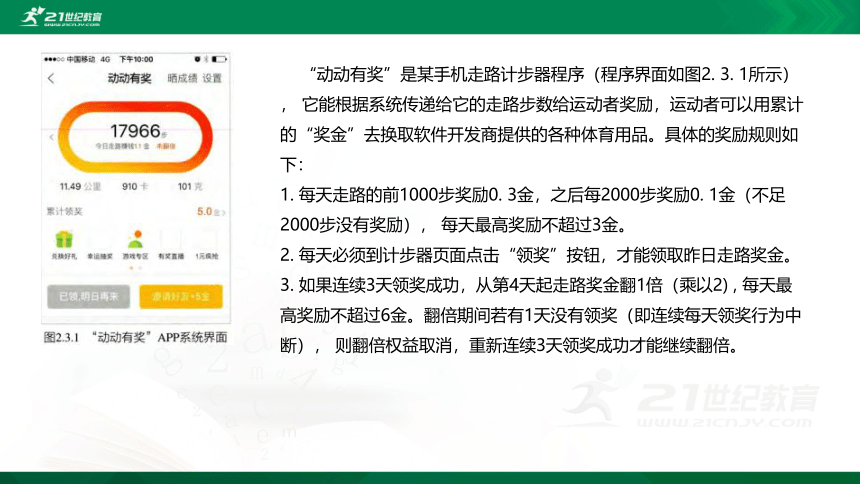
“动动有奖”是某手机走路计步器程序(程序界面如图2. 3. 1所示), 它能根据系统传递给它的走路步数给运动者奖励,运动者可以用累计的“奖金”去换取软件开发商提供的各种体育用品。具体的奖励规则如下:
1. 每天走路的前1000步奖励0. 3金,之后每2000步奖励0. 1金(不足2000步没有奖励), 每天最高奖励不超过3金。
2. 每天必须到计步器页面点击“领奖”按钮,才能领取昨日走路奖金。
3. 如果连续3天领奖成功,从第4天起走路奖金翻1倍(乘以2) , 每天最高奖励不超过6金。翻倍期间若有1天没有领奖(即连续每天领奖行为中断), 则翻倍权益取消,重新连续3天领奖成功才能继续翻倍。
第一步:抽象与建模
抽象与建模指的是从现实项目的真实情境中提炼出核心的要素并加以确定或假设,最终定义出一个有明确已知条件和求解目标的问题,并用数学符号描述解决该问题的计算模型。
X表示每天走路的步数
F 表示是否成功领取了每天的奖金(1表示成功领取,0表示没有领取)。
n表示需要统计走路的天数
1. 提炼核心要素并加以确定或假设
已知n (1≤n≤30) 组数据:Xi , Fi (1≤i≤n) , 计算“奖金”总和total。
其中total=ΣSi, Si=
n
i=1
(Fi=0)
(Fi=1且Fi-1, Fi-2, Fi-3, 不全为1)
(Fi=1且Fi-1,Fi-2,Fi-3.全为1)
0
0.3
0.3+ (X-1000)-2000 x0.1
3
注: 了表示对表达式的值向下取整。
如果有下列4组数据:
Xi=4500, F1=1; X2=9870, F2=1; X3=12890, F3=0; X4 =57890, F4 =1.
则根据上述计算模型得到的 “奖金”总和为4. 1金。
(Xi <1000)
(1000≤Xi <3000)
(3000≤xi≤55000)
(55000t=
2、用数学符号描述解决问题的计算模型
0????2????
?
第二步:设计算法
输入数据
处理数据
输出结果
按照“自顶向下、逐步细化”的结构化设计思想,对前面的算法细化:
①输人总天数n 。
②表示天数的变量i初始化为1。
③若i≤n, 则转④, 否则转⑦。
④输人第i天的数据(包括第i天走路步数Xi, 是否成功领取i天“奖金”的标记Fi ) 。
⑤根据当前输入的数据Xi, Fi 统计该天领取的奖金并累加到总奖金total中。
⑥表示天数的变量i增加1, 然后转③。
⑦输出变量total的值。
拓展链接:
常用算法介绍
本例采用模拟策略来设计算法,即根据现实事务的实际流程和要求逐步进行处理,以达到数据处理的目标。计算机科学家根据各种问题的模型特征提出了各种针对性的算法设计策略,如穷举算法、顺序查找算法、对分查找算法、冒泡排序算法、深度优先搜索法以及动态规划等。
?思考与练习:
上述算法中,“按照奖励规则第1条计算“奖金'! ”在两个环节中出现,请根据算法功能完成下列练习。
(1) 改进算法,使得算法中只有一个环节出现“按照奖励规则第1条计算“奖金‘t ”。
(2) 请进一步细化原算法中的“按照奖励规则第1条计算'奖金‘t ”, 并用流程图进行描述。
1. 任意输入三个数,输出其中最小数的值。设计解决该问题的算法并用流程图描述该算法。
2. 任意输入三个数,按从小到大的顺序依次输出这三个数。设计解决该问题的算法并用流程图描述该算法。
巩固与提高:
3. 以下哪个步骤不属于用算法解决问题的过程(B)
A. 抽象与建模 B. 问题界定
C. 设计算法 D. 描述算法
4. 将两位同学的身高放入变量a和b中,比较这两个变量的大小,最后把其中较大的数放到变量c中并输出,流程图如图所示。①中应填(B)
A.aB.a>b
C.a=b
D.a<>b
参考答案:
1、
2、
第一步;输入3个整数a,b,c。
第二步:将a与b比较,并把大者赋给b, 小者赋给a。
第三步:将a与c比较,并把大者赋给c, 小者赋给a, 此时a已是三者中最小的。
第四步:将b与c比较,并把大者赋给c, 小者赋给b, 此时a,b,c已按从小到大的顺序排列好。
第五步:按顺序输出a,b,c。
谢 谢!
Thanks!
https://www.21cnjy.com/help/help_extract.php
浙教版(2019版) 信息技术(高中)
必修1 数据与计算
2.3 用算法解决问题的过程
学习目标
1
2
3
抽象与建模
设计算法
描述算法
1
2
重点难点
重点:抽象与建模,设计算法。
难点:抽象与建模,设计算法。
课堂导入
用计算机解决问题时,由于实际问题情境的复杂性,需要对实际问题进行抽象与建模,再根据建立的计算模型设计算法,并将算法用合适的方式加以准确描述。
“动动有奖”是某手机走路计步器程序(程序界面如图2. 3. 1所示), 它能根据系统传递给它的走路步数给运动者奖励,运动者可以用累计的“奖金”去换取软件开发商提供的各种体育用品。具体的奖励规则如下:
1. 每天走路的前1000步奖励0. 3金,之后每2000步奖励0. 1金(不足2000步没有奖励), 每天最高奖励不超过3金。
2. 每天必须到计步器页面点击“领奖”按钮,才能领取昨日走路奖金。
3. 如果连续3天领奖成功,从第4天起走路奖金翻1倍(乘以2) , 每天最高奖励不超过6金。翻倍期间若有1天没有领奖(即连续每天领奖行为中断), 则翻倍权益取消,重新连续3天领奖成功才能继续翻倍。
第一步:抽象与建模
抽象与建模指的是从现实项目的真实情境中提炼出核心的要素并加以确定或假设,最终定义出一个有明确已知条件和求解目标的问题,并用数学符号描述解决该问题的计算模型。
X表示每天走路的步数
F 表示是否成功领取了每天的奖金(1表示成功领取,0表示没有领取)。
n表示需要统计走路的天数
1. 提炼核心要素并加以确定或假设
已知n (1≤n≤30) 组数据:Xi , Fi (1≤i≤n) , 计算“奖金”总和total。
其中total=ΣSi, Si=
n
i=1
(Fi=0)
(Fi=1且Fi-1, Fi-2, Fi-3, 不全为1)
(Fi=1且Fi-1,Fi-2,Fi-3.全为1)
0
0.3
0.3+ (X-1000)-2000 x0.1
3
注: 了表示对表达式的值向下取整。
如果有下列4组数据:
Xi=4500, F1=1; X2=9870, F2=1; X3=12890, F3=0; X4 =57890, F4 =1.
则根据上述计算模型得到的 “奖金”总和为4. 1金。
(Xi <1000)
(1000≤Xi <3000)
(3000≤xi≤55000)
(55000
2、用数学符号描述解决问题的计算模型
0????2????
?
第二步:设计算法
输入数据
处理数据
输出结果
按照“自顶向下、逐步细化”的结构化设计思想,对前面的算法细化:
①输人总天数n 。
②表示天数的变量i初始化为1。
③若i≤n, 则转④, 否则转⑦。
④输人第i天的数据(包括第i天走路步数Xi, 是否成功领取i天“奖金”的标记Fi ) 。
⑤根据当前输入的数据Xi, Fi 统计该天领取的奖金并累加到总奖金total中。
⑥表示天数的变量i增加1, 然后转③。
⑦输出变量total的值。
拓展链接:
常用算法介绍
本例采用模拟策略来设计算法,即根据现实事务的实际流程和要求逐步进行处理,以达到数据处理的目标。计算机科学家根据各种问题的模型特征提出了各种针对性的算法设计策略,如穷举算法、顺序查找算法、对分查找算法、冒泡排序算法、深度优先搜索法以及动态规划等。
?思考与练习:
上述算法中,“按照奖励规则第1条计算“奖金'! ”在两个环节中出现,请根据算法功能完成下列练习。
(1) 改进算法,使得算法中只有一个环节出现“按照奖励规则第1条计算“奖金‘t ”。
(2) 请进一步细化原算法中的“按照奖励规则第1条计算'奖金‘t ”, 并用流程图进行描述。
1. 任意输入三个数,输出其中最小数的值。设计解决该问题的算法并用流程图描述该算法。
2. 任意输入三个数,按从小到大的顺序依次输出这三个数。设计解决该问题的算法并用流程图描述该算法。
巩固与提高:
3. 以下哪个步骤不属于用算法解决问题的过程(B)
A. 抽象与建模 B. 问题界定
C. 设计算法 D. 描述算法
4. 将两位同学的身高放入变量a和b中,比较这两个变量的大小,最后把其中较大的数放到变量c中并输出,流程图如图所示。①中应填(B)
A.aB.a>b
C.a=b
D.a<>b
参考答案:
1、
2、
第一步;输入3个整数a,b,c。
第二步:将a与b比较,并把大者赋给b, 小者赋给a。
第三步:将a与c比较,并把大者赋给c, 小者赋给a, 此时a已是三者中最小的。
第四步:将b与c比较,并把大者赋给c, 小者赋给b, 此时a,b,c已按从小到大的顺序排列好。
第五步:按顺序输出a,b,c。
谢 谢!
Thanks!
https://www.21cnjy.com/help/help_extract.php
