【单元培优卷】 第3章 数据分析初步(含解析)
文档属性
| 名称 | 【单元培优卷】 第3章 数据分析初步(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年浙教版八年级下册数学
单元测评培优卷(原版+解析版)
第3章数据分析初步
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·浙江八年级)某班10名学生体育测试的成绩(单位:分)分别为:58,60,59,52,58,55,57,58,49,57,则这组数据的众数、中位数分别为(
)
A.58,57.5
B.57,57.5
C.58,58
D.58,57
2.(2020·辽宁抚顺·初二期末)某专卖店专门营销某种品牌的运动服,店主对上一周中运动服的销售情况统计如下:
尺码
号
号
号
号
号
平均每天销售数量(套)
该店主本周进货时,增加了一些号的运动服,影响该店主决策的统计量是(
)
A.平均数
B.众数
C.方差
D.中位数
3.(2020·南阳市油田教育教学研究室八年级期末)甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级
参赛人数
平均数
中位数
方差
甲
45
83
86
82
乙
45
83
84
135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;②乙班优秀的人数少于甲班优秀的人数(竞赛得分分为优秀);③甲班成绩的波动性比乙班小.上述结论中正确的个数是(
)
A.3个
B.2个
C.1个
D.0个
4.(2020·广西八年级期末)某市招聘老师的笔试和面试的成绩均按百分制计,并且分别按40%和60%来计算综合成绩.王老师本次招聘考试的笔试成绩为90分,面试成绩为85分,经计算他的综合成绩是(
)
A.85分
B.87分
C.87.5分
D.90分
5.(2020·浙江八年级期末)小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是(
)
A.小时
B.小时
C.或小时
D.或或小时
6.(2020·辽宁八年级期末)学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价
元
元
元
元
数目
本
本
本
本
下列说法正确的是(
)
A.该班级所售图书的总收入是元
B.在该班级所传图书价格组成的一组数据中,中位数是元
C.在该班级所售图书价格组成的一组数据中,众数是元
D.在该班级所售图书价格组成的一组数据中,平均数是元
7.(2020·河北辛集·期末)一组数据:3,4,4,4,5.若拿掉一个数据4,则发生变化的统计量是(
)
A.极差
B.方差
C.中位数
D.众数
8.(2020·江苏鼓楼·初三其他)2019年12月26日是中国伟大领袖毛泽东同志诞辰126周年纪念日.某校举行以“高楼万丈平地起,幸福不忘毛主席”为主题的演讲比赛,最终有15名同学进入决赛(他们决赛的成绩各不相同),比赛将评出一等奖1名,二等奖2名,三等奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他需要知道这15名学生成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
9.(2020·福建翔安·其他)小明在最近五次数学测试中,前四次的成绩分别是96分、98分、94分和92分,第五次因病只得了45分,则代表小明数学学的数据是这五次数学成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
10.(2020·温州外国语学校八年级月考)有11个正整数,平均数是10,中位数是9,众数只有一个8,问最大的正整数最大为(
)
A.25
B.30
C.35
D.40
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·济南育英中学八年级期末)某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加若干次测试成绩中随机抽取8次,计算得两人的平均成绩都是85分,方差分别是=35.5,=41,从操作技能稳定的角度考虑,选派__________参加比赛;
12.(2020·北京北师大实验中学九年级)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是_____.
①年用水量超过180m3且不超过240m3的居民家庭按第二档水价交费;
②该市居民家庭年用水量的平均数不超过180;③该市居民家庭年用水量的中位数在90﹣150之间;
④该市居民家庭年用水量的众数在90﹣120之间.
13.(2020·全国初三单元测试)下表为某班学生成绩的次数分配表.已知全班共有人,且众数为分,中位数为分,则之值为________.
成绩(分)
次数(人)
14.(2020·衡阳市逸夫中学九年级月考)一组数据:1,-2,a的平均数是0,那么这组数据的方差是____
15.(2019·浙江八年级月考)在篮球赛中,选手小明在第六、第七、第八、第九场比赛中分别得了23分、14分、11分和20分,他的前九场的平均成绩高于前五场的平均成绩,如果他的前十场的平均成绩高于18分,那么他的第十场比赛的成绩至少为__________分.
16.(2020·江苏镇江·中考真题)在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为_____.
17.(2020·四川外国语大学附属外国语学校八年级期中)重庆实验外国语学校是一所外语小班制教学的特色学校,初二年级某英语小班共有名同学,学号依次为号,号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东(号)调整到甲组,将丙组的小英(号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加,乙组同学学号的平均数将比调整前增加;同时乙组的小强(号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学.
18.(2020·阳新县木港镇东春初级中学九年级)已知数据,,,的平均数为m,方差为,则数据,,,的平均数为________,方差为_________,标准差为_________.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·四川武侯·)某公司销售部有营销员15人,销售部为了制定关于某种商品的每位营销员的个人月销售定额,统计了这15人某月关于此商品的个人月销售量(单位:件)如下:
个人月销售量
1800
510
250
210
150
120
营销员人数
1
1
3
5
3
2
(1)求这15位营销员该月关于此商品的个人月销售量的平均数,并直接写出这组数据的中位数和众数;(2)假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件,你认为对多数营销员是否合理?并在(1)的基础上说明理由.
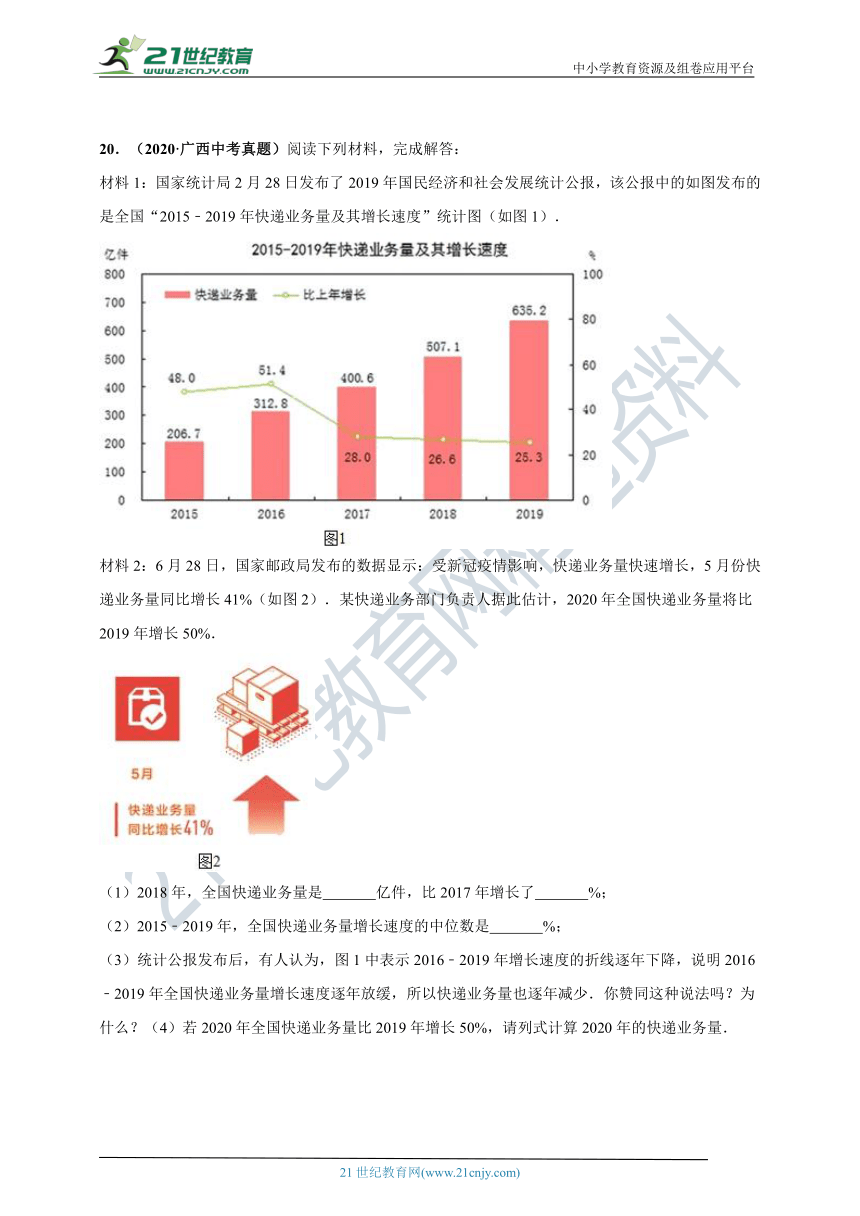
20.(2020·广西中考真题)阅读下列材料,完成解答:
材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).
材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.
(1)2018年,全国快递业务量是
亿件,比2017年增长了
%;
(2)2015﹣2019年,全国快递业务量增长速度的中位数是
%;
(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.
21.(2020·重庆九年级)《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱.某学校为了提高学生的诗词水平,倡导全校3000名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的条形和扇形统计图如图所示.
(整理、描述数据):
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”:
一周诗词背数量
3首
4首
5首
6首
7首
8首
人数
16
24
32
78
35
(分析数据):
平均数
中位数
众数
大赛之前
5
大赛之后
6
6
6
请根据调查的信息分析:(1)补全条形统计图;(2)计算首,首,首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;(3)根据调查的相关数据,选择适当的统计量评价该校经典诗词诵背系列活动的效果.
22.(2020·环县环城初级中学八年级期末)某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表,另全班50位同学则参与民主测评进行投票,结果如图:
规定:演讲得分按“去掉一个最高分和一个最低分
再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分
(1)求甲、乙两位选手各自演讲答辩的平均分;(2)试求民主测评统计图中a、b的值是多少(3)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长.
23.(2020·河南八年级期末)在学校举办的一次文艺汇演比赛中,八(1)班和八(2)班参加表演比赛的女生身高(单位:)分别是:
八(1)班:163,164,165,165,165,165,166,167.
八(2)班:162,164,164,165,166,166,166,167.
(1)把表格补充完整
身高班级
平均数
中位数
众数
八(1)班
165
165
165
八(2)班
165
(2)从数据来看,哪个班女生的身高更整齐?请你从方差的角度说明理由.
24.(2020·禹城市莒镇中学初二期末)申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表:
(1)要评价两家餐饮店日营业额的平均水平,你选择什么统计量?求出这个统计量;
(2)分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1);(3)你能预测明年黄金周中哪几天营业额会比较高吗?说说你的理由.
25.(2020·江西南康·其他)某厂生产A、B两种产品,其单价随市场变化而作相应调整,营销人员根据前三次单价变化的情况,绘制了下列统计表及不完整的折线图,并求得了A产品三次单价的平均数和方差:
,.
A、B产品单价变化统计表
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
根据以上信息,回答下列问题:(1)补全图中B产品单价变化的折线图;(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
2020-2021学年浙教版八年级下册数学
单元测评培优卷(原版+解析版)
第3章数据分析初步
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·浙江八年级)某班10名学生体育测试的成绩(单位:分)分别为:58,60,59,52,58,55,57,58,49,57,则这组数据的众数、中位数分别为(
)
A.58,57.5
B.57,57.5
C.58,58
D.58,57
【答案】A
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【详解】解:数据58出现了3次,出现次数最多,故这组数据的众数是58;
将这组数据从小到大的顺序排列49,52,55,57,57,58,58,58,59,60,
∴中位数是(57+58)÷2=57.5.故选:A.
【点睛】本题考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
2.(2020·辽宁抚顺·初二期末)某专卖店专门营销某种品牌的运动服,店主对上一周中运动服的销售情况统计如下:
尺码
号
号
号
号
号
平均每天销售数量(套)
该店主本周进货时,增加了一些号的运动服,影响该店主决策的统计量是(
)
A.平均数
B.众数
C.方差
D.中位数
【答案】B
【分析】根据表格数据,销售量最多的为M号,因此影响该店主增加了一些号的运动服的是众数.
【解析】解:由于众数是数据中出现次数最多的数,故影响该店主决策的统计量是众数.故答案选B
【点睛】本题主要考查了平均数,众数,方差,中位数的定义,熟记理解各数据的定义是解题的关键.
3.(2020·南阳市油田教育教学研究室八年级期末)甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级
参赛人数
平均数
中位数
方差
甲
45
83
86
82
乙
45
83
84
135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;②乙班优秀的人数少于甲班优秀的人数(竞赛得分分为优秀);③甲班成绩的波动性比乙班小.上述结论中正确的个数是(
)
A.3个
B.2个
C.1个
D.0个
【答案】A
【分析】根据平均数、中位数、方差的定义即可判断.
【详解】解:由表格可知,甲、乙两班学生的成绩平均成绩相同;
根据中位数可以确定,乙班优秀的人数少于甲班优秀的人数;
根据方差可知,甲班成绩的波动性比乙班小.故①②③正确,故选:A.
【点睛】本题考查了平均数、中位数、方差等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.(2020·广西八年级期末)某市招聘老师的笔试和面试的成绩均按百分制计,并且分别按40%和60%来计算综合成绩.王老师本次招聘考试的笔试成绩为90分,面试成绩为85分,经计算他的综合成绩是(
)
A.85分
B.87分
C.87.5分
D.90分
【答案】B
【分析】根据笔试和面试所占的百分比以及笔试成绩和面试成绩,列出算式,进行计算即可.
【详解】解:王老师的综合成绩为:90×40%+85×60%=87(分),故选:B.
【点睛】此题考查了加权平均数,关键是根据加权平均数的计算公式列出算式,用到的知识点是加权平均数.
5.(2020·浙江八年级期末)小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是(
)
A.小时
B.小时
C.或小时
D.或或小时
【答案】C
【分析】利用众数及中位数的定义解答即可.
【详解】解:当第五位同学的课外阅读时间为4小时时,此时五个数据为4,4,5,8,10,众数为4,中位数为5,不合题意;
当第五位同学的课外阅读时间为5小时时,此时五个数据为4,5,5,8,10,众数为5,中位数为5,符合题意;
当第五位同学的课外阅读时间为8小时时,此时五个数据为4,5,8,8,10,众数为8,中位数为8,符合题意;
当第五位同学的课外阅读时间为10小时时,此时五个数据为4,5,8,10,10,众数为10,中位数为8,不合题意;故第五位同学的每周课外阅读时间为5或8小时.故答案为C.
【点睛】本题考查了众数及中位数的概念,解题的关键是根申请题意,并结合题意分类讨论解答.
6.(2020·辽宁八年级期末)学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价
元
元
元
元
数目
本
本
本
本
下列说法正确的是(
)
A.该班级所售图书的总收入是元
B.在该班级所传图书价格组成的一组数据中,中位数是元
C.在该班级所售图书价格组成的一组数据中,众数是元
D.在该班级所售图书价格组成的一组数据中,平均数是元
【答案】A
【分析】把所有数据相加可对A进行判断;利用中位数和众数的定义对B、C进行判断;利用平均数的计算公式计算出这组数据的平均,从而可对D进行判断.
【详解】A、该班级所售图书的总收入为3×14+4×11+5×10+6×15=226,所以A选项正确;
B、共50本书,第25个数为4,第26个数为5,所以这组数据的中位数为4.5,所以B选项错误;
C、这组数据的众数为6,所以C选项错误;
D、这组数据的平均数为,所以D选项错误.故选:A.
【点睛】本题考查计算中位数,众数和平均数,熟练掌握它们的计算方法是解题的关键.
7.(2020·河北辛集·期末)一组数据:3,4,4,4,5.若拿掉一个数据4,则发生变化的统计量是(
)
A.极差
B.方差
C.中位数
D.众数
【答案】B
【分析】依据定义和公式分别计算新旧两组数据的极差、方差、中位数、众数,由此即可求解.
【解析】原数据3,4,4,4,5的极差为5-3=2,原数据3,4,4,4,5的中位数为4,
原数据3,4,4,4,5的众数为4,原数据3,4,4,4,5的平均数为=4,
原数据3,4,4,4,5的方差为×[(3-4)2+(4-4)2×3+(5-4)2]=0.4;
新数据的3,4,4,5的极差为5-3=2,新数据的3,4,4,5的中位数为(4+4)÷2=4,
新数据的3,4,4,5的众数为4,新数据的3,4,4,5的平均数为=4,
新数据的3,4,4,5的方差为×[(3-4)2+(4-4)2×2+(5-4)2]=0.5;
∴添加一个数据4,方差发生变化,故选B.
【点睛】本题主要考查的是众数、中位数、方差、极差,熟练掌握相关概念和公式是解题的关键.
8.(2020·江苏鼓楼·初三其他)2019年12月26日是中国伟大领袖毛泽东同志诞辰126周年纪念日.某校举行以“高楼万丈平地起,幸福不忘毛主席”为主题的演讲比赛,最终有15名同学进入决赛(他们决赛的成绩各不相同),比赛将评出一等奖1名,二等奖2名,三等奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他需要知道这15名学生成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
【答案】D
【分析】根据进入决赛的15名同学所得分数互不相同,所以这15名同学所得分数的中位数低于获奖的学生中的最低分,所以某参赛选手知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,据此解答即可.
【解析】∵进入决赛的15名学生所得分数互不相同,共有1+2+4=7个奖项,
∴这15名同学所得分数的中位数低于获奖的学生中的最低分,
∴某参赛选手知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,
如果这名参赛选手的分数大于中位数,则他能获奖,
如果这名参赛选手的分数小于或等于中位数,则他不能获奖.故选:D.
【点睛】此题主要考查了统计量的选择,要熟练掌握,解答此题的关键是要明确:数据的平均数、众数、中位数是描述一组数据集中趋势的特征量,属于基础题,难度不大.
9.(2020·福建翔安·其他)小明在最近五次数学测试中,前四次的成绩分别是96分、98分、94分和92分,第五次因病只得了45分,则代表小明数学学的数据是这五次数学成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
【答案】D
【解析】解:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数,只有中位数能代表小明数学学
故选:D.
【点睛】本题主要考查了对平均数、众数、中位数、方差的理解,结合具体的实例进行准确分析.
10.(2020·温州外国语学校八年级月考)有11个正整数,平均数是10,中位数是9,众数只有一个8,问最大的正整数最大为(
)
A.25
B.30
C.35
D.40
【答案】C
【分析】最大数出现的条件就是前面10个数的和尽可能小,而它们的和是110,中间的是9,则其它的越小,剩下的就越大,但是8的个数要多于其它的,可分8的个数分别是2,3,4,5时,讨论写出符合条件的数据即得答案.
【详解】解:∵有11个正整数,平均数是10,∴这11个数的和为110,
由于中位数是9,众数只有一个8,
如有两个8,则其他数至多1个,符合条件的数据可以是:1,2,3,8,8,9,10,11,12,13,x;
如有3个8,9是中位数,则其他数至多2个,符合条件的数据可以是:1,1,8,8,8,9,9,10,10,11,x;
如有4个8,则其他数至多3个,符合条件的数据可以是:1,8,8,8,8,9,9,9,10,10,x;
如有5个8,则其他数至多4个,符合条件的数据可以是:8,8,8,8,8,9,9,9,9,10,x;
再根据其和为110,比较上面各组数据中哪个x更大即可,通过计算x分别为33,35,30,24,
故最大的正整数为35.故选:C.
【点睛】本题主要考查了众数、平均数以及中位数的运用,解题时注意:一组数据中出现次数最多的数据叫做众数.将一组数据按照从小到大(或从大到小)的顺序排列,则处于中间位置的数(或中间位置的两个数的平均数)就是这组数据的中位数.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·济南育英中学八年级期末)某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加若干次测试成绩中随机抽取8次,计算得两人的平均成绩都是85分,方差分别是=35.5,=41,从操作技能稳定的角度考虑,选派__________参加比赛;
【答案】甲
【分析】根据方差的意义即可得到结论.
【详解】解:∵S甲2=35.5,S乙2=41,乙的方差大于甲的方差,
∴甲的成绩稳定∴选甲参加合适.故答案为:甲.
【点睛】本题考查了方差,牢记方差的意义解决本题的关键.
13.(2020·北京北师大实验中学九年级)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是_____.
①年用水量超过180m3且不超过240m3的居民家庭按第二档水价交费;
②该市居民家庭年用水量的平均数不超过180;
③该市居民家庭年用水量的中位数在90﹣150之间;
④该市居民家庭年用水量的众数在90﹣120之间.
【答案】①②④.
【分析】利用条形统计图结合平均数、中位数和众数的定义分别分析即可得出答案.
【详解】解:①由条形统计图可得:年用水量超过180m3且不超过240m3的居民家庭一共有(0.4+0.25)=0.65(万),
×100%=13%,年用水量超过180m3且不超过240m3的居民家庭按第二档水价交费,正确;
②年用水量不超过180m3的该市居民家庭一共有(0.25+0.75+1.5+1.0+0.5)=4(万),
×100%=80%,则该市居民家庭年用水量的平均数不超过180,正确;
③∵5万个数据的中间是第25000和25001的平均数,
∴该市居民家庭年用水量的中位数在120﹣150之间,故此选项错误;
④该市居民家庭年用水量的众数在90﹣120之间,正确,
则推断合理的是①②④;故答案为:①②④.
【点睛】此题主要考查了频数分布直方图以及中位数和众数的定义,正确利用条形统计图获取正确信息是解题关键.
13.(2020·全国初三单元测试)下表为某班学生成绩的次数分配表.已知全班共有人,且众数为分,中位数为分,则之值为________.
成绩(分)
次数(人)
【答案】57
【分析】由于全班共有38人,则x+y=38-(2+3+5+6+3+4)=15,结合众数为50分,中位数为60分,分情况讨论即可确定x、y之值,从而求出x2-y之值.
【解析】∵全班共有38人,∴x+y=38-(2+3+5+6+3+4)=15,
又∵众数为50分,∴x>6,x>y,∴x≥8,
当x=8时,y=7,中位数是第19、20两个数的平均数,都为60分,则中位数为60分,符合题意;
当x=9时,y=6,中位数是第19、20两个数的平均数,则中位数为(50+60)÷2=55分,不符合题意;
同理当x=10,11,12,13,14,15时,中位数都不等于60分,不符合题意.
∴x=8,y=7.∴x2-y=64-7=57.故答案为:57.
【点睛】本题结合代数式求值考查了众数与中位数的意义.众数是一组数据中出现次数最多的数据,注意众数可以不止一个;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.本题的关键是确定x、y之值.
14.(2020·衡阳市逸夫中学九年级月考)一组数据:1,-2,a的平均数是0,那么这组数据的方差是____
【答案】2
【分析】先由平均数的公式计算出a的值,再根据方差公式计算.
【详解】解:三个数:1,-2,a的平均数是0,则有
解得a=1,
∴方差.故答案为:2.
【点睛】本题考查方差、平均数的计算,熟悉相关运算法则是解题的关键.
15.(2019·浙江八年级月考)在篮球赛中,选手小明在第六、第七、第八、第九场比赛中分别得了23分、14分、11分和20分,他的前九场的平均成绩高于前五场的平均成绩,如果他的前十场的平均成绩高于18分,那么他的第十场比赛的成绩至少为__________分.
【答案】29
【分析】设他第十场的成绩为x分,首先求得第六场到第九场的平均成绩?为17分,进而可得前五场该选手的得的总分最多为17×5?1=84分,再根据他前十场的平均成绩高于18分列不等式求出即可.
【详解】解:设他第十场的成绩为x分,
第六场到第九场的平均成绩为?=17(分),超过了前五场的平均成绩,
因此,前五场该选手得的总分最多为17×5?1=84(分),
由于他前十场的平均成绩高于18分,
则x+(23+14+11+20)+84≥18×10+1,解得:x≥29.故答案为:29.
【点睛】本题考查一元一次不等式的应用.解决问题的关键是读懂题意,依题意列出不等式进行求解.
16.(2020·江苏镇江·中考真题)在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为_____.
【答案】1
【分析】原来五个数的中位数是6,如果再加入一个数,变成了偶数个数,则中位数是中间两位数的平均数,由此可知加入的一个数是6,再根据平均数的公式得到关于x的方程,解方程即可求解.
【解析】解:从小到大排列的五个数x,3,6,8,12的中位数是6,
∵再加入一个数,这六个数的中位数与原来五个数的中位数相等,∴加入的一个数是6,
∵这六个数的平均数与原来五个数的平均数相等,
∴解得x=1.故答案为:1.
【点睛】本题考查了确定一组数据的中位数和平均数,熟悉相关性质是解题的关键.
17.(2020·四川外国语大学附属外国语学校八年级期中)重庆实验外国语学校是一所外语小班制教学的特色学校,初二年级某英语小班共有名同学,学号依次为号,号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东(号)调整到甲组,将丙组的小英(号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加,乙组同学学号的平均数将比调整前增加;同时乙组的小强(号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学.
【答案】6
【分析】设甲、乙、丙组调整前的人数分别是,,,则甲、乙、丙调整后的人数分别是,,,设甲、乙、丙组调整前各组的号码之和分别为,,,则甲、乙、丙调整后各组的号码之和分别为,,,根据题意得,由③得,则,求出,,由,得出,则,即可得出结果.
【详解】解:设甲、乙、丙组调整前的人数分别是,,,则甲、乙、丙调整后的人数分别是,,,
设甲、乙、丙组调整前各组的号码之和分别为,,,则甲、乙、丙调整后各组的号码之和分别为,,,
根据题意得:,
由③得:,,即,④
④代入②整理得:,由①得:,,
,,,为正整数,,故答案为:6.
【点睛】本题考查了平均数、一元一次不等式的应用等知识;由乙组的人数在调整前和调整后是不变的,总分多了6分,平均分多了0.6分,求出乙组的人数是解题的关键.
18.(2020·阳新县木港镇东春初级中学九年级)已知数据,,,的平均数为m,方差为,则数据,,,的平均数为________,方差为_________,标准差为_________.
【答案】
ks
【分析】根据平均数、方差、标准差的定义列式计算即可.
【详解】数据,,,的平均数为m,方差为,
,,
,
数据,,,的平均数为,
数据,,,的方差为,标准差为.
故答案为;;ks.
【点睛】本题考查了平均数、方差、标准差,熟记平均数、方差、标准差的定义是解题的关键.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·四川武侯·)某公司销售部有营销员15人,销售部为了制定关于某种商品的每位营销员的个人月销售定额,统计了这15人某月关于此商品的个人月销售量(单位:件)如下:
个人月销售量
1800
510
250
210
150
120
营销员人数
1
1
3
5
3
2
(1)求这15位营销员该月关于此商品的个人月销售量的平均数,并直接写出这组数据的中位数和众数;
(2)假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件,你认为对多数营销员是否合理?并在(1)的基础上说明理由.
【答案】(1)平均数320,中位数210,众数210;(2)不合理,理由见解析.
【分析】(1)根据平均数的定义以及计算公式、中位数的定义、众数的定义求解即可.
(2)根据平均数、中位数、众数的定义进行分析即可.
【解析】(1)平均数是:
(1800+510+25×3+210×5+150×3+120×2)=320(件),
表中的数据是按从大到小的顺序排列的,处于中间位置的是210,因而中位数是210(件),
210出现了5次最多,所以众数是210;
(2)不合理.因为15人中有13人的销售额不到320件,320件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平.销售额定为210件合适些,因为210件既是中位数,又是众数,是大部分人能达到的定额.
【点睛】本题考查了数据统计的问题,掌握平均数的定义以及计算公式、中位数的定义、众数的定义是解题的关键.
20.(2020·广西中考真题)阅读下列材料,完成解答:
材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).
材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.
(1)2018年,全国快递业务量是
亿件,比2017年增长了
%;
(2)2015﹣2019年,全国快递业务量增长速度的中位数是
%;
(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?
(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.
【答案】(1)507.1,26.6;(2)28;(3)不赞同,理由详见解析;(4)2020年的快递业务量为952.82亿件.
【分析】(1)由材料1中的统计图中的信息即可得到结论;
(2)由材料1中的统计图的信息结合中位数的含义即可得到结论;
(3)根据统计图中的信息即可得到结论;
(4)根据题意列式:,再计算即可.
【解析】解:(1)由材料1中的统计图可得:2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;
故答案为:
(2)由材料1中的统计图可得:2015﹣2019年,全国快递业务量增长速度分别为
由小大到大排列为
所以全国快递业务量增长速度的中位数是28%;故答案为:
(3)不赞同,理由:由图1中的信息可得,2016﹣2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;
(4)635.2×(1+50%)=952.82,答:2020年的快递业务量为952.82亿件.
【点睛】本题考查的是从统计图中获取信息,同时考查了中位数的含义,掌握以上知识是解题的关键.
21.(2020·重庆九年级)《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱.某学校为了提高学生的诗词水平,倡导全校3000名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的条形和扇形统计图如图所示.
(整理、描述数据):
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”:
一周诗词背数量
3首
4首
5首
6首
7首
8首
人数
16
24
32
78
35
(分析数据):
平均数
中位数
众数
大赛之前
5
大赛之后
6
6
6
请根据调查的信息分析:(1)补全条形统计图;(2)计算首,首,首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;(3)根据调查的相关数据,选择适当的统计量评价该校经典诗词诵背系列活动的效果.
【答案】(1)补全图形见解析;(2)55,4.5,4;2100人;(3)平均数,中位数和众数
【分析】(1)根据条形统计图和扇形统计图中的数据可以解答本题;
(2)根据中位数和众数的概念及样本估计总体思想的运用求解可得;
(3)根据统计图和表格中的数据可以分别计算出比赛前后的众数和中位数,从而可以解答本题.
【详解】解:(1)被抽查的学生总人数为40÷=240(人),
∴4首的人数为240×=90(人),
补全图形如下:
(2)a=240-(16+24+32+78+35)=55,b==4.5,c=4,
估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数为:
3000×=2100(人),故答案为:55、4.5、4;
(3)活动启动之初的中位数是4.5首,众数是4首,大赛比赛后一个月时的中位数是6首,众数是6首,由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想.
【点睛】本题考查扇形统计图、条形统计图、用样本估计总体、统计量的选择,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
22.(2020·环县环城初级中学八年级期末)某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表,另全班50位同学则参与民主测评进行投票,结果如图:
规定:演讲得分按“去掉一个最高分和一个最低分
再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分
(1)求甲、乙两位选手各自演讲答辩的平均分;(2)试求民主测评统计图中a、b的值是多少(3)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长.
【答案】(1)甲:92;乙:89;(2)a=7,b=4;(3)应选择甲当班长
【分析】(1)根据求平均数公式:,结合题意,按“去掉一个最高分和一个最低分再算平均分”的方法,即可求出甲、乙两位选手各自演讲答辩的平均分.
(2)a、b的值分别表示甲、乙两同学进行演讲答辩后,所得的“较好”票数.根据“较好”票数=投票总数50-“好”票数-“一般”票数即可求出.
(3)首先根据平均数的概念分别计算出甲、乙两位选手的民主测评分,再由(1)中求出的两位选手各自演讲答辩的平均分,最后根据不同权重计算加权成绩.
【详解】解:(1)甲演讲答辩的平均分为:;
乙演讲答辩的平均分为:.
(2)a=50-40-3=7;b=50-42-4=4.
(3)甲民主测评分为:40×2+7=87,乙民主测评分为:42×2+4=88,
∴甲综合得分:,∴乙综合得分:,∴应选择甲当班长.
【点睛】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.
23.(2020·河南八年级期末)在学校举办的一次文艺汇演比赛中,八(1)班和八(2)班参加表演比赛的女生身高(单位:)分别是:
八(1)班:163,164,165,165,165,165,166,167.
八(2)班:162,164,164,165,166,166,166,167.
(1)把表格补充完整
身高班级
平均数
中位数
众数
八(1)班
165
165
165
八(2)班
165
(2)从数据来看,哪个班女生的身高更整齐?请你从方差的角度说明理由.
【答案】(1)填表见解析;(2)八(1)班女生的身高更整齐;答案见解析.
【分析】(1)根据中位数的定义,可求解中位数;根据众数的定义,可求解众数;
(2)求出每个班级参与汇演的女生身高的方差,再比较大小即可求解.
【详解】(1)
身高班级
平均数
中位数
众数
八(1)班
165
165
165
八(2)班
165
165.5
166
(2)解:将两组数据都减去165得:
八(1)班:-2,-1,0,0,0,0,1,2;
八(2)班:-3,-1,-1,0,1,1,1,2
八(1)班方差:
八(2)班方差:
∵∴八(1)班女生的身高更整齐.
【点睛】本题考查中位数和众数及方差的求法,理解中位数和众数的概念及掌握方差的公式是解题的关键.
24.(2020·禹城市莒镇中学初二期末)申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表:
(1)要评价两家餐饮店日营业额的平均水平,你选择什么统计量?求出这个统计量;
(2)分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1);(3)你能预测明年黄金周中哪几天营业额会比较高吗?说说你的理由.
【答案】(1)选择平均数,A店的日营业额的平均值是2.5百万元,B店的日营业额的平均值是2.5百万元;(2)A组新数据的方差约为1.0,B组新数据的方差约为0.6;(3)答案见解析.
分析:(1)在数据差别不是很大的情况下评价平均水平一般采用平均数;
(2)分别用每一个数据减去其平均数,得到新数据后计算其方差后比较即可;
(3)用今年的数据大体反映明年的数据即可.
【解析】
(1)选择平均数.
A店的日营业额的平均值是×(1+1.6+3.5+4+2.7+2.5+2.2)=2.5(百万元),
B店的日营业额的平均值是×(1.9+1.9+2.7+3.8+3.2+2.1+1.9)=2.5(百万元).
(2)0.6,1.9,0.5,-1.3,-0.2,-0.3;
B组数据的新数为0,0.8,1.1,-0.6,-1.1,-0.2,
∴A组新数据的平均数
xA=×(0.6+1.9+0.5-1.3-0.2-0.3)=0.2(百万元),
B组新数据的平均数xB=×(0+0.8+1.1-0.6-1.1-0.2)=0(百万元).
∴A组新数据的方差s=×[(0.2-0.6)2+(0.2-1.9)2+(0.2-0.5)2+(0.2+1.3)2+(0.2+0.2)2+(0.2+0.3)2]≈1.0,
B组新数据的方差s=×(02+0.82+1.12+0.62+1.12+0.22)≈0.6.
这两个方差的大小反映了A,B两家餐饮店相邻两天的日营业额的变化情况,并且B餐饮店相邻两天的日营业额的变化情况比较小.
(3)观察今年黄金周的数据发现今年的3号、4号、5号营业额较高,故明年的3号、4号、5号营业额可能较高.
点睛:本题考查了算术平均数和方差的计算,算术平均数的计算公式是:,方差的计算公式为:,根据公式求解即可.
25.(2020·江西南康·其他)某厂生产A、B两种产品,其单价随市场变化而作相应调整,营销人员根据前三次单价变化的情况,绘制了下列统计表及不完整的折线图,并求得了A产品三次单价的平均数和方差:
,.
A、B产品单价变化统计表
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
根据以上信息,回答下列问题:(1)补全图中B产品单价变化的折线图;(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
【答案】(1)答案见解析;(2)0.167;B产品波动小;(3)25
【分析】(1)根据题目提供数据补充折线统计图即可;(2)计算B产品平均数及方差即可;
(3)首先确定这四次单价的中位数,然后确定第四次调价的范围,根据“A产品这四次单价的中位数是B产品四次单价中位数的2倍少1”列式求m即可.
【解析】.(1)补全折线图如下图所示:
(2),.
∵,即,
∴B产品的单价波动小;
(3)第四次调价后,对于A产品,这四次单价的中位数为.
对于B产品,∵m>0,∴第四次单价必大于3.
∵,∴第四次单价小于4.∴,解得.
答:的值是25.
【点睛】本题考查了方差、折线统计图、算术平均数、中位数的知识,解题的关键是根据方差公式进行有关的运算,有点难度.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年浙教版八年级下册数学
单元测评培优卷(原版+解析版)
第3章数据分析初步
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·浙江八年级)某班10名学生体育测试的成绩(单位:分)分别为:58,60,59,52,58,55,57,58,49,57,则这组数据的众数、中位数分别为(
)
A.58,57.5
B.57,57.5
C.58,58
D.58,57
2.(2020·辽宁抚顺·初二期末)某专卖店专门营销某种品牌的运动服,店主对上一周中运动服的销售情况统计如下:
尺码
号
号
号
号
号
平均每天销售数量(套)
该店主本周进货时,增加了一些号的运动服,影响该店主决策的统计量是(
)
A.平均数
B.众数
C.方差
D.中位数
3.(2020·南阳市油田教育教学研究室八年级期末)甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级
参赛人数
平均数
中位数
方差
甲
45
83
86
82
乙
45
83
84
135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;②乙班优秀的人数少于甲班优秀的人数(竞赛得分分为优秀);③甲班成绩的波动性比乙班小.上述结论中正确的个数是(
)
A.3个
B.2个
C.1个
D.0个
4.(2020·广西八年级期末)某市招聘老师的笔试和面试的成绩均按百分制计,并且分别按40%和60%来计算综合成绩.王老师本次招聘考试的笔试成绩为90分,面试成绩为85分,经计算他的综合成绩是(
)
A.85分
B.87分
C.87.5分
D.90分
5.(2020·浙江八年级期末)小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是(
)
A.小时
B.小时
C.或小时
D.或或小时
6.(2020·辽宁八年级期末)学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价
元
元
元
元
数目
本
本
本
本
下列说法正确的是(
)
A.该班级所售图书的总收入是元
B.在该班级所传图书价格组成的一组数据中,中位数是元
C.在该班级所售图书价格组成的一组数据中,众数是元
D.在该班级所售图书价格组成的一组数据中,平均数是元
7.(2020·河北辛集·期末)一组数据:3,4,4,4,5.若拿掉一个数据4,则发生变化的统计量是(
)
A.极差
B.方差
C.中位数
D.众数
8.(2020·江苏鼓楼·初三其他)2019年12月26日是中国伟大领袖毛泽东同志诞辰126周年纪念日.某校举行以“高楼万丈平地起,幸福不忘毛主席”为主题的演讲比赛,最终有15名同学进入决赛(他们决赛的成绩各不相同),比赛将评出一等奖1名,二等奖2名,三等奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他需要知道这15名学生成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
9.(2020·福建翔安·其他)小明在最近五次数学测试中,前四次的成绩分别是96分、98分、94分和92分,第五次因病只得了45分,则代表小明数学学的数据是这五次数学成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
10.(2020·温州外国语学校八年级月考)有11个正整数,平均数是10,中位数是9,众数只有一个8,问最大的正整数最大为(
)
A.25
B.30
C.35
D.40
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·济南育英中学八年级期末)某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加若干次测试成绩中随机抽取8次,计算得两人的平均成绩都是85分,方差分别是=35.5,=41,从操作技能稳定的角度考虑,选派__________参加比赛;
12.(2020·北京北师大实验中学九年级)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是_____.
①年用水量超过180m3且不超过240m3的居民家庭按第二档水价交费;
②该市居民家庭年用水量的平均数不超过180;③该市居民家庭年用水量的中位数在90﹣150之间;
④该市居民家庭年用水量的众数在90﹣120之间.
13.(2020·全国初三单元测试)下表为某班学生成绩的次数分配表.已知全班共有人,且众数为分,中位数为分,则之值为________.
成绩(分)
次数(人)
14.(2020·衡阳市逸夫中学九年级月考)一组数据:1,-2,a的平均数是0,那么这组数据的方差是____
15.(2019·浙江八年级月考)在篮球赛中,选手小明在第六、第七、第八、第九场比赛中分别得了23分、14分、11分和20分,他的前九场的平均成绩高于前五场的平均成绩,如果他的前十场的平均成绩高于18分,那么他的第十场比赛的成绩至少为__________分.
16.(2020·江苏镇江·中考真题)在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为_____.
17.(2020·四川外国语大学附属外国语学校八年级期中)重庆实验外国语学校是一所外语小班制教学的特色学校,初二年级某英语小班共有名同学,学号依次为号,号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东(号)调整到甲组,将丙组的小英(号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加,乙组同学学号的平均数将比调整前增加;同时乙组的小强(号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学.
18.(2020·阳新县木港镇东春初级中学九年级)已知数据,,,的平均数为m,方差为,则数据,,,的平均数为________,方差为_________,标准差为_________.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·四川武侯·)某公司销售部有营销员15人,销售部为了制定关于某种商品的每位营销员的个人月销售定额,统计了这15人某月关于此商品的个人月销售量(单位:件)如下:
个人月销售量
1800
510
250
210
150
120
营销员人数
1
1
3
5
3
2
(1)求这15位营销员该月关于此商品的个人月销售量的平均数,并直接写出这组数据的中位数和众数;(2)假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件,你认为对多数营销员是否合理?并在(1)的基础上说明理由.
20.(2020·广西中考真题)阅读下列材料,完成解答:
材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).
材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.
(1)2018年,全国快递业务量是
亿件,比2017年增长了
%;
(2)2015﹣2019年,全国快递业务量增长速度的中位数是
%;
(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.
21.(2020·重庆九年级)《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱.某学校为了提高学生的诗词水平,倡导全校3000名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的条形和扇形统计图如图所示.
(整理、描述数据):
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”:
一周诗词背数量
3首
4首
5首
6首
7首
8首
人数
16
24
32
78
35
(分析数据):
平均数
中位数
众数
大赛之前
5
大赛之后
6
6
6
请根据调查的信息分析:(1)补全条形统计图;(2)计算首,首,首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;(3)根据调查的相关数据,选择适当的统计量评价该校经典诗词诵背系列活动的效果.
22.(2020·环县环城初级中学八年级期末)某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表,另全班50位同学则参与民主测评进行投票,结果如图:
规定:演讲得分按“去掉一个最高分和一个最低分
再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分
(1)求甲、乙两位选手各自演讲答辩的平均分;(2)试求民主测评统计图中a、b的值是多少(3)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长.
23.(2020·河南八年级期末)在学校举办的一次文艺汇演比赛中,八(1)班和八(2)班参加表演比赛的女生身高(单位:)分别是:
八(1)班:163,164,165,165,165,165,166,167.
八(2)班:162,164,164,165,166,166,166,167.
(1)把表格补充完整
身高班级
平均数
中位数
众数
八(1)班
165
165
165
八(2)班
165
(2)从数据来看,哪个班女生的身高更整齐?请你从方差的角度说明理由.
24.(2020·禹城市莒镇中学初二期末)申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表:
(1)要评价两家餐饮店日营业额的平均水平,你选择什么统计量?求出这个统计量;
(2)分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1);(3)你能预测明年黄金周中哪几天营业额会比较高吗?说说你的理由.
25.(2020·江西南康·其他)某厂生产A、B两种产品,其单价随市场变化而作相应调整,营销人员根据前三次单价变化的情况,绘制了下列统计表及不完整的折线图,并求得了A产品三次单价的平均数和方差:
,.
A、B产品单价变化统计表
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
根据以上信息,回答下列问题:(1)补全图中B产品单价变化的折线图;(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
2020-2021学年浙教版八年级下册数学
单元测评培优卷(原版+解析版)
第3章数据分析初步
(测试时间:120分钟,满分:120分)
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2020·浙江八年级)某班10名学生体育测试的成绩(单位:分)分别为:58,60,59,52,58,55,57,58,49,57,则这组数据的众数、中位数分别为(
)
A.58,57.5
B.57,57.5
C.58,58
D.58,57
【答案】A
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【详解】解:数据58出现了3次,出现次数最多,故这组数据的众数是58;
将这组数据从小到大的顺序排列49,52,55,57,57,58,58,58,59,60,
∴中位数是(57+58)÷2=57.5.故选:A.
【点睛】本题考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
2.(2020·辽宁抚顺·初二期末)某专卖店专门营销某种品牌的运动服,店主对上一周中运动服的销售情况统计如下:
尺码
号
号
号
号
号
平均每天销售数量(套)
该店主本周进货时,增加了一些号的运动服,影响该店主决策的统计量是(
)
A.平均数
B.众数
C.方差
D.中位数
【答案】B
【分析】根据表格数据,销售量最多的为M号,因此影响该店主增加了一些号的运动服的是众数.
【解析】解:由于众数是数据中出现次数最多的数,故影响该店主决策的统计量是众数.故答案选B
【点睛】本题主要考查了平均数,众数,方差,中位数的定义,熟记理解各数据的定义是解题的关键.
3.(2020·南阳市油田教育教学研究室八年级期末)甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级
参赛人数
平均数
中位数
方差
甲
45
83
86
82
乙
45
83
84
135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;②乙班优秀的人数少于甲班优秀的人数(竞赛得分分为优秀);③甲班成绩的波动性比乙班小.上述结论中正确的个数是(
)
A.3个
B.2个
C.1个
D.0个
【答案】A
【分析】根据平均数、中位数、方差的定义即可判断.
【详解】解:由表格可知,甲、乙两班学生的成绩平均成绩相同;
根据中位数可以确定,乙班优秀的人数少于甲班优秀的人数;
根据方差可知,甲班成绩的波动性比乙班小.故①②③正确,故选:A.
【点睛】本题考查了平均数、中位数、方差等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.(2020·广西八年级期末)某市招聘老师的笔试和面试的成绩均按百分制计,并且分别按40%和60%来计算综合成绩.王老师本次招聘考试的笔试成绩为90分,面试成绩为85分,经计算他的综合成绩是(
)
A.85分
B.87分
C.87.5分
D.90分
【答案】B
【分析】根据笔试和面试所占的百分比以及笔试成绩和面试成绩,列出算式,进行计算即可.
【详解】解:王老师的综合成绩为:90×40%+85×60%=87(分),故选:B.
【点睛】此题考查了加权平均数,关键是根据加权平均数的计算公式列出算式,用到的知识点是加权平均数.
5.(2020·浙江八年级期末)小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是(
)
A.小时
B.小时
C.或小时
D.或或小时
【答案】C
【分析】利用众数及中位数的定义解答即可.
【详解】解:当第五位同学的课外阅读时间为4小时时,此时五个数据为4,4,5,8,10,众数为4,中位数为5,不合题意;
当第五位同学的课外阅读时间为5小时时,此时五个数据为4,5,5,8,10,众数为5,中位数为5,符合题意;
当第五位同学的课外阅读时间为8小时时,此时五个数据为4,5,8,8,10,众数为8,中位数为8,符合题意;
当第五位同学的课外阅读时间为10小时时,此时五个数据为4,5,8,10,10,众数为10,中位数为8,不合题意;故第五位同学的每周课外阅读时间为5或8小时.故答案为C.
【点睛】本题考查了众数及中位数的概念,解题的关键是根申请题意,并结合题意分类讨论解答.
6.(2020·辽宁八年级期末)学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价
元
元
元
元
数目
本
本
本
本
下列说法正确的是(
)
A.该班级所售图书的总收入是元
B.在该班级所传图书价格组成的一组数据中,中位数是元
C.在该班级所售图书价格组成的一组数据中,众数是元
D.在该班级所售图书价格组成的一组数据中,平均数是元
【答案】A
【分析】把所有数据相加可对A进行判断;利用中位数和众数的定义对B、C进行判断;利用平均数的计算公式计算出这组数据的平均,从而可对D进行判断.
【详解】A、该班级所售图书的总收入为3×14+4×11+5×10+6×15=226,所以A选项正确;
B、共50本书,第25个数为4,第26个数为5,所以这组数据的中位数为4.5,所以B选项错误;
C、这组数据的众数为6,所以C选项错误;
D、这组数据的平均数为,所以D选项错误.故选:A.
【点睛】本题考查计算中位数,众数和平均数,熟练掌握它们的计算方法是解题的关键.
7.(2020·河北辛集·期末)一组数据:3,4,4,4,5.若拿掉一个数据4,则发生变化的统计量是(
)
A.极差
B.方差
C.中位数
D.众数
【答案】B
【分析】依据定义和公式分别计算新旧两组数据的极差、方差、中位数、众数,由此即可求解.
【解析】原数据3,4,4,4,5的极差为5-3=2,原数据3,4,4,4,5的中位数为4,
原数据3,4,4,4,5的众数为4,原数据3,4,4,4,5的平均数为=4,
原数据3,4,4,4,5的方差为×[(3-4)2+(4-4)2×3+(5-4)2]=0.4;
新数据的3,4,4,5的极差为5-3=2,新数据的3,4,4,5的中位数为(4+4)÷2=4,
新数据的3,4,4,5的众数为4,新数据的3,4,4,5的平均数为=4,
新数据的3,4,4,5的方差为×[(3-4)2+(4-4)2×2+(5-4)2]=0.5;
∴添加一个数据4,方差发生变化,故选B.
【点睛】本题主要考查的是众数、中位数、方差、极差,熟练掌握相关概念和公式是解题的关键.
8.(2020·江苏鼓楼·初三其他)2019年12月26日是中国伟大领袖毛泽东同志诞辰126周年纪念日.某校举行以“高楼万丈平地起,幸福不忘毛主席”为主题的演讲比赛,最终有15名同学进入决赛(他们决赛的成绩各不相同),比赛将评出一等奖1名,二等奖2名,三等奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他需要知道这15名学生成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
【答案】D
【分析】根据进入决赛的15名同学所得分数互不相同,所以这15名同学所得分数的中位数低于获奖的学生中的最低分,所以某参赛选手知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,据此解答即可.
【解析】∵进入决赛的15名学生所得分数互不相同,共有1+2+4=7个奖项,
∴这15名同学所得分数的中位数低于获奖的学生中的最低分,
∴某参赛选手知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是中位数,
如果这名参赛选手的分数大于中位数,则他能获奖,
如果这名参赛选手的分数小于或等于中位数,则他不能获奖.故选:D.
【点睛】此题主要考查了统计量的选择,要熟练掌握,解答此题的关键是要明确:数据的平均数、众数、中位数是描述一组数据集中趋势的特征量,属于基础题,难度不大.
9.(2020·福建翔安·其他)小明在最近五次数学测试中,前四次的成绩分别是96分、98分、94分和92分,第五次因病只得了45分,则代表小明数学学的数据是这五次数学成绩的(
)
A.平均数
B.方差
C.众数
D.中位数
【答案】D
【解析】解:中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数,只有中位数能代表小明数学学
故选:D.
【点睛】本题主要考查了对平均数、众数、中位数、方差的理解,结合具体的实例进行准确分析.
10.(2020·温州外国语学校八年级月考)有11个正整数,平均数是10,中位数是9,众数只有一个8,问最大的正整数最大为(
)
A.25
B.30
C.35
D.40
【答案】C
【分析】最大数出现的条件就是前面10个数的和尽可能小,而它们的和是110,中间的是9,则其它的越小,剩下的就越大,但是8的个数要多于其它的,可分8的个数分别是2,3,4,5时,讨论写出符合条件的数据即得答案.
【详解】解:∵有11个正整数,平均数是10,∴这11个数的和为110,
由于中位数是9,众数只有一个8,
如有两个8,则其他数至多1个,符合条件的数据可以是:1,2,3,8,8,9,10,11,12,13,x;
如有3个8,9是中位数,则其他数至多2个,符合条件的数据可以是:1,1,8,8,8,9,9,10,10,11,x;
如有4个8,则其他数至多3个,符合条件的数据可以是:1,8,8,8,8,9,9,9,10,10,x;
如有5个8,则其他数至多4个,符合条件的数据可以是:8,8,8,8,8,9,9,9,9,10,x;
再根据其和为110,比较上面各组数据中哪个x更大即可,通过计算x分别为33,35,30,24,
故最大的正整数为35.故选:C.
【点睛】本题主要考查了众数、平均数以及中位数的运用,解题时注意:一组数据中出现次数最多的数据叫做众数.将一组数据按照从小到大(或从大到小)的顺序排列,则处于中间位置的数(或中间位置的两个数的平均数)就是这组数据的中位数.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2020·济南育英中学八年级期末)某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加若干次测试成绩中随机抽取8次,计算得两人的平均成绩都是85分,方差分别是=35.5,=41,从操作技能稳定的角度考虑,选派__________参加比赛;
【答案】甲
【分析】根据方差的意义即可得到结论.
【详解】解:∵S甲2=35.5,S乙2=41,乙的方差大于甲的方差,
∴甲的成绩稳定∴选甲参加合适.故答案为:甲.
【点睛】本题考查了方差,牢记方差的意义解决本题的关键.
13.(2020·北京北师大实验中学九年级)为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是_____.
①年用水量超过180m3且不超过240m3的居民家庭按第二档水价交费;
②该市居民家庭年用水量的平均数不超过180;
③该市居民家庭年用水量的中位数在90﹣150之间;
④该市居民家庭年用水量的众数在90﹣120之间.
【答案】①②④.
【分析】利用条形统计图结合平均数、中位数和众数的定义分别分析即可得出答案.
【详解】解:①由条形统计图可得:年用水量超过180m3且不超过240m3的居民家庭一共有(0.4+0.25)=0.65(万),
×100%=13%,年用水量超过180m3且不超过240m3的居民家庭按第二档水价交费,正确;
②年用水量不超过180m3的该市居民家庭一共有(0.25+0.75+1.5+1.0+0.5)=4(万),
×100%=80%,则该市居民家庭年用水量的平均数不超过180,正确;
③∵5万个数据的中间是第25000和25001的平均数,
∴该市居民家庭年用水量的中位数在120﹣150之间,故此选项错误;
④该市居民家庭年用水量的众数在90﹣120之间,正确,
则推断合理的是①②④;故答案为:①②④.
【点睛】此题主要考查了频数分布直方图以及中位数和众数的定义,正确利用条形统计图获取正确信息是解题关键.
13.(2020·全国初三单元测试)下表为某班学生成绩的次数分配表.已知全班共有人,且众数为分,中位数为分,则之值为________.
成绩(分)
次数(人)
【答案】57
【分析】由于全班共有38人,则x+y=38-(2+3+5+6+3+4)=15,结合众数为50分,中位数为60分,分情况讨论即可确定x、y之值,从而求出x2-y之值.
【解析】∵全班共有38人,∴x+y=38-(2+3+5+6+3+4)=15,
又∵众数为50分,∴x>6,x>y,∴x≥8,
当x=8时,y=7,中位数是第19、20两个数的平均数,都为60分,则中位数为60分,符合题意;
当x=9时,y=6,中位数是第19、20两个数的平均数,则中位数为(50+60)÷2=55分,不符合题意;
同理当x=10,11,12,13,14,15时,中位数都不等于60分,不符合题意.
∴x=8,y=7.∴x2-y=64-7=57.故答案为:57.
【点睛】本题结合代数式求值考查了众数与中位数的意义.众数是一组数据中出现次数最多的数据,注意众数可以不止一个;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.本题的关键是确定x、y之值.
14.(2020·衡阳市逸夫中学九年级月考)一组数据:1,-2,a的平均数是0,那么这组数据的方差是____
【答案】2
【分析】先由平均数的公式计算出a的值,再根据方差公式计算.
【详解】解:三个数:1,-2,a的平均数是0,则有
解得a=1,
∴方差.故答案为:2.
【点睛】本题考查方差、平均数的计算,熟悉相关运算法则是解题的关键.
15.(2019·浙江八年级月考)在篮球赛中,选手小明在第六、第七、第八、第九场比赛中分别得了23分、14分、11分和20分,他的前九场的平均成绩高于前五场的平均成绩,如果他的前十场的平均成绩高于18分,那么他的第十场比赛的成绩至少为__________分.
【答案】29
【分析】设他第十场的成绩为x分,首先求得第六场到第九场的平均成绩?为17分,进而可得前五场该选手的得的总分最多为17×5?1=84分,再根据他前十场的平均成绩高于18分列不等式求出即可.
【详解】解:设他第十场的成绩为x分,
第六场到第九场的平均成绩为?=17(分),超过了前五场的平均成绩,
因此,前五场该选手得的总分最多为17×5?1=84(分),
由于他前十场的平均成绩高于18分,
则x+(23+14+11+20)+84≥18×10+1,解得:x≥29.故答案为:29.
【点睛】本题考查一元一次不等式的应用.解决问题的关键是读懂题意,依题意列出不等式进行求解.
16.(2020·江苏镇江·中考真题)在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为_____.
【答案】1
【分析】原来五个数的中位数是6,如果再加入一个数,变成了偶数个数,则中位数是中间两位数的平均数,由此可知加入的一个数是6,再根据平均数的公式得到关于x的方程,解方程即可求解.
【解析】解:从小到大排列的五个数x,3,6,8,12的中位数是6,
∵再加入一个数,这六个数的中位数与原来五个数的中位数相等,∴加入的一个数是6,
∵这六个数的平均数与原来五个数的平均数相等,
∴解得x=1.故答案为:1.
【点睛】本题考查了确定一组数据的中位数和平均数,熟悉相关性质是解题的关键.
17.(2020·四川外国语大学附属外国语学校八年级期中)重庆实验外国语学校是一所外语小班制教学的特色学校,初二年级某英语小班共有名同学,学号依次为号,号,……20号,现随机分成甲、乙、丙三个小组,每组人数若干.若将乙组的小东(号)调整到甲组,将丙组的小英(号)调整到乙组,此时甲、丙两组同学学号的平均数都将比调整前增加,乙组同学学号的平均数将比调整前增加;同时乙组的小强(号)经过计算发现,他的学号数高于调整前乙组同学学号的平均数,却低于调整后乙组的平均数则调整前甲组共有_____名同学.
【答案】6
【分析】设甲、乙、丙组调整前的人数分别是,,,则甲、乙、丙调整后的人数分别是,,,设甲、乙、丙组调整前各组的号码之和分别为,,,则甲、乙、丙调整后各组的号码之和分别为,,,根据题意得,由③得,则,求出,,由,得出,则,即可得出结果.
【详解】解:设甲、乙、丙组调整前的人数分别是,,,则甲、乙、丙调整后的人数分别是,,,
设甲、乙、丙组调整前各组的号码之和分别为,,,则甲、乙、丙调整后各组的号码之和分别为,,,
根据题意得:,
由③得:,,即,④
④代入②整理得:,由①得:,,
,,,为正整数,,故答案为:6.
【点睛】本题考查了平均数、一元一次不等式的应用等知识;由乙组的人数在调整前和调整后是不变的,总分多了6分,平均分多了0.6分,求出乙组的人数是解题的关键.
18.(2020·阳新县木港镇东春初级中学九年级)已知数据,,,的平均数为m,方差为,则数据,,,的平均数为________,方差为_________,标准差为_________.
【答案】
ks
【分析】根据平均数、方差、标准差的定义列式计算即可.
【详解】数据,,,的平均数为m,方差为,
,,
,
数据,,,的平均数为,
数据,,,的方差为,标准差为.
故答案为;;ks.
【点睛】本题考查了平均数、方差、标准差,熟记平均数、方差、标准差的定义是解题的关键.
三、解答题(本大题共7小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2020·四川武侯·)某公司销售部有营销员15人,销售部为了制定关于某种商品的每位营销员的个人月销售定额,统计了这15人某月关于此商品的个人月销售量(单位:件)如下:
个人月销售量
1800
510
250
210
150
120
营销员人数
1
1
3
5
3
2
(1)求这15位营销员该月关于此商品的个人月销售量的平均数,并直接写出这组数据的中位数和众数;
(2)假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件,你认为对多数营销员是否合理?并在(1)的基础上说明理由.
【答案】(1)平均数320,中位数210,众数210;(2)不合理,理由见解析.
【分析】(1)根据平均数的定义以及计算公式、中位数的定义、众数的定义求解即可.
(2)根据平均数、中位数、众数的定义进行分析即可.
【解析】(1)平均数是:
(1800+510+25×3+210×5+150×3+120×2)=320(件),
表中的数据是按从大到小的顺序排列的,处于中间位置的是210,因而中位数是210(件),
210出现了5次最多,所以众数是210;
(2)不合理.因为15人中有13人的销售额不到320件,320件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平.销售额定为210件合适些,因为210件既是中位数,又是众数,是大部分人能达到的定额.
【点睛】本题考查了数据统计的问题,掌握平均数的定义以及计算公式、中位数的定义、众数的定义是解题的关键.
20.(2020·广西中考真题)阅读下列材料,完成解答:
材料1:国家统计局2月28日发布了2019年国民经济和社会发展统计公报,该公报中的如图发布的是全国“2015﹣2019年快递业务量及其增长速度”统计图(如图1).
材料2:6月28日,国家邮政局发布的数据显示:受新冠疫情影响,快递业务量快速增长,5月份快递业务量同比增长41%(如图2).某快递业务部门负责人据此估计,2020年全国快递业务量将比2019年增长50%.
(1)2018年,全国快递业务量是
亿件,比2017年增长了
%;
(2)2015﹣2019年,全国快递业务量增长速度的中位数是
%;
(3)统计公报发布后,有人认为,图1中表示2016﹣2019年增长速度的折线逐年下降,说明2016﹣2019年全国快递业务量增长速度逐年放缓,所以快递业务量也逐年减少.你赞同这种说法吗?为什么?
(4)若2020年全国快递业务量比2019年增长50%,请列式计算2020年的快递业务量.
【答案】(1)507.1,26.6;(2)28;(3)不赞同,理由详见解析;(4)2020年的快递业务量为952.82亿件.
【分析】(1)由材料1中的统计图中的信息即可得到结论;
(2)由材料1中的统计图的信息结合中位数的含义即可得到结论;
(3)根据统计图中的信息即可得到结论;
(4)根据题意列式:,再计算即可.
【解析】解:(1)由材料1中的统计图可得:2018年,全国快递业务量是507.1亿件,比2017年增长了26.6%;
故答案为:
(2)由材料1中的统计图可得:2015﹣2019年,全国快递业务量增长速度分别为
由小大到大排列为
所以全国快递业务量增长速度的中位数是28%;故答案为:
(3)不赞同,理由:由图1中的信息可得,2016﹣2019年全国快递业务量增长速度逐年放缓,但是快递业务量却逐年增加;
(4)635.2×(1+50%)=952.82,答:2020年的快递业务量为952.82亿件.
【点睛】本题考查的是从统计图中获取信息,同时考查了中位数的含义,掌握以上知识是解题的关键.
21.(2020·重庆九年级)《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱.某学校为了提高学生的诗词水平,倡导全校3000名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的条形和扇形统计图如图所示.
(整理、描述数据):
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”:
一周诗词背数量
3首
4首
5首
6首
7首
8首
人数
16
24
32
78
35
(分析数据):
平均数
中位数
众数
大赛之前
5
大赛之后
6
6
6
请根据调查的信息分析:(1)补全条形统计图;(2)计算首,首,首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;(3)根据调查的相关数据,选择适当的统计量评价该校经典诗词诵背系列活动的效果.
【答案】(1)补全图形见解析;(2)55,4.5,4;2100人;(3)平均数,中位数和众数
【分析】(1)根据条形统计图和扇形统计图中的数据可以解答本题;
(2)根据中位数和众数的概念及样本估计总体思想的运用求解可得;
(3)根据统计图和表格中的数据可以分别计算出比赛前后的众数和中位数,从而可以解答本题.
【详解】解:(1)被抽查的学生总人数为40÷=240(人),
∴4首的人数为240×=90(人),
补全图形如下:
(2)a=240-(16+24+32+78+35)=55,b==4.5,c=4,
估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数为:
3000×=2100(人),故答案为:55、4.5、4;
(3)活动启动之初的中位数是4.5首,众数是4首,大赛比赛后一个月时的中位数是6首,众数是6首,由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想.
【点睛】本题考查扇形统计图、条形统计图、用样本估计总体、统计量的选择,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
22.(2020·环县环城初级中学八年级期末)某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,A、B、C、D、E五位老师作为评委,对演讲答辩情况进行评价,结果如下表,另全班50位同学则参与民主测评进行投票,结果如图:
规定:演讲得分按“去掉一个最高分和一个最低分
再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分
(1)求甲、乙两位选手各自演讲答辩的平均分;(2)试求民主测评统计图中a、b的值是多少(3)若按演讲答辩得分和民主测评6:4的权重比计算两位选手的综合得分,则应选取哪位选手当班长.
【答案】(1)甲:92;乙:89;(2)a=7,b=4;(3)应选择甲当班长
【分析】(1)根据求平均数公式:,结合题意,按“去掉一个最高分和一个最低分再算平均分”的方法,即可求出甲、乙两位选手各自演讲答辩的平均分.
(2)a、b的值分别表示甲、乙两同学进行演讲答辩后,所得的“较好”票数.根据“较好”票数=投票总数50-“好”票数-“一般”票数即可求出.
(3)首先根据平均数的概念分别计算出甲、乙两位选手的民主测评分,再由(1)中求出的两位选手各自演讲答辩的平均分,最后根据不同权重计算加权成绩.
【详解】解:(1)甲演讲答辩的平均分为:;
乙演讲答辩的平均分为:.
(2)a=50-40-3=7;b=50-42-4=4.
(3)甲民主测评分为:40×2+7=87,乙民主测评分为:42×2+4=88,
∴甲综合得分:,∴乙综合得分:,∴应选择甲当班长.
【点睛】本题考查了平均数和加权平均数的概念及应用,以及从统计图中获取信息的能力.
23.(2020·河南八年级期末)在学校举办的一次文艺汇演比赛中,八(1)班和八(2)班参加表演比赛的女生身高(单位:)分别是:
八(1)班:163,164,165,165,165,165,166,167.
八(2)班:162,164,164,165,166,166,166,167.
(1)把表格补充完整
身高班级
平均数
中位数
众数
八(1)班
165
165
165
八(2)班
165
(2)从数据来看,哪个班女生的身高更整齐?请你从方差的角度说明理由.
【答案】(1)填表见解析;(2)八(1)班女生的身高更整齐;答案见解析.
【分析】(1)根据中位数的定义,可求解中位数;根据众数的定义,可求解众数;
(2)求出每个班级参与汇演的女生身高的方差,再比较大小即可求解.
【详解】(1)
身高班级
平均数
中位数
众数
八(1)班
165
165
165
八(2)班
165
165.5
166
(2)解:将两组数据都减去165得:
八(1)班:-2,-1,0,0,0,0,1,2;
八(2)班:-3,-1,-1,0,1,1,1,2
八(1)班方差:
八(2)班方差:
∵∴八(1)班女生的身高更整齐.
【点睛】本题考查中位数和众数及方差的求法,理解中位数和众数的概念及掌握方差的公式是解题的关键.
24.(2020·禹城市莒镇中学初二期末)申遗成功后的杭州,在国庆黄金周旅游市场中的知名餐饮受游客追捧,西湖景区附近的A,B两家餐饮店在这一周内的日营业额如下表:
(1)要评价两家餐饮店日营业额的平均水平,你选择什么统计量?求出这个统计量;
(2)分别求出两家餐饮店各相邻两天的日营业额变化数量,得出两组新数据,然后求出两组新数据的方差,这两个方差的大小反映了什么?(结果精确到0.1);(3)你能预测明年黄金周中哪几天营业额会比较高吗?说说你的理由.
【答案】(1)选择平均数,A店的日营业额的平均值是2.5百万元,B店的日营业额的平均值是2.5百万元;(2)A组新数据的方差约为1.0,B组新数据的方差约为0.6;(3)答案见解析.
分析:(1)在数据差别不是很大的情况下评价平均水平一般采用平均数;
(2)分别用每一个数据减去其平均数,得到新数据后计算其方差后比较即可;
(3)用今年的数据大体反映明年的数据即可.
【解析】
(1)选择平均数.
A店的日营业额的平均值是×(1+1.6+3.5+4+2.7+2.5+2.2)=2.5(百万元),
B店的日营业额的平均值是×(1.9+1.9+2.7+3.8+3.2+2.1+1.9)=2.5(百万元).
(2)0.6,1.9,0.5,-1.3,-0.2,-0.3;
B组数据的新数为0,0.8,1.1,-0.6,-1.1,-0.2,
∴A组新数据的平均数
xA=×(0.6+1.9+0.5-1.3-0.2-0.3)=0.2(百万元),
B组新数据的平均数xB=×(0+0.8+1.1-0.6-1.1-0.2)=0(百万元).
∴A组新数据的方差s=×[(0.2-0.6)2+(0.2-1.9)2+(0.2-0.5)2+(0.2+1.3)2+(0.2+0.2)2+(0.2+0.3)2]≈1.0,
B组新数据的方差s=×(02+0.82+1.12+0.62+1.12+0.22)≈0.6.
这两个方差的大小反映了A,B两家餐饮店相邻两天的日营业额的变化情况,并且B餐饮店相邻两天的日营业额的变化情况比较小.
(3)观察今年黄金周的数据发现今年的3号、4号、5号营业额较高,故明年的3号、4号、5号营业额可能较高.
点睛:本题考查了算术平均数和方差的计算,算术平均数的计算公式是:,方差的计算公式为:,根据公式求解即可.
25.(2020·江西南康·其他)某厂生产A、B两种产品,其单价随市场变化而作相应调整,营销人员根据前三次单价变化的情况,绘制了下列统计表及不完整的折线图,并求得了A产品三次单价的平均数和方差:
,.
A、B产品单价变化统计表
第一次
第二次
第三次
A产品单价(元/件)
6
5.2
6.5
B产品单价(元/件)
3.5
4
3
根据以上信息,回答下列问题:(1)补全图中B产品单价变化的折线图;(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
【答案】(1)答案见解析;(2)0.167;B产品波动小;(3)25
【分析】(1)根据题目提供数据补充折线统计图即可;(2)计算B产品平均数及方差即可;
(3)首先确定这四次单价的中位数,然后确定第四次调价的范围,根据“A产品这四次单价的中位数是B产品四次单价中位数的2倍少1”列式求m即可.
【解析】.(1)补全折线图如下图所示:
(2),.
∵,即,
∴B产品的单价波动小;
(3)第四次调价后,对于A产品,这四次单价的中位数为.
对于B产品,∵m>0,∴第四次单价必大于3.
∵,∴第四次单价小于4.∴,解得.
答:的值是25.
【点睛】本题考查了方差、折线统计图、算术平均数、中位数的知识,解题的关键是根据方差公式进行有关的运算,有点难度.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
