第五章一元一次方程期末复习

(共60张PPT)
第五章 一元一次方程
教学目标：
　　1、使学生进一步理解一元一次方程的有关概念。
　　2、掌握一元一次方程的解法步骤，熟练地解一元一次方程。
　　3、能以一元一次方程为工具解决实际问题，提高分析问题，解决问题的能力及激发学生学数学的热情。
重难点：
　　利用一元一次方程解决实际问题
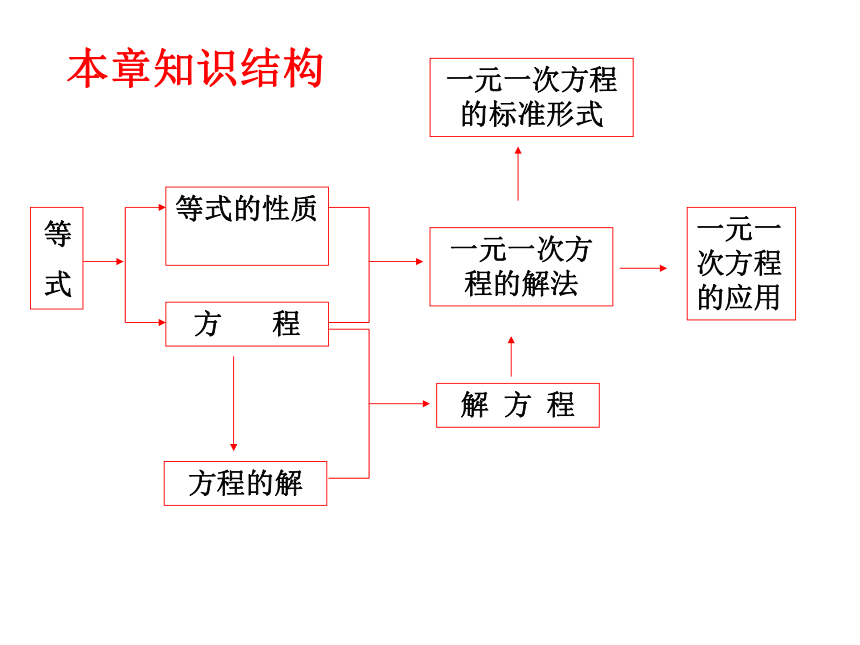
本章知识结构
等 式
等式的性质
方 程
一元一次方程的解法
一元一次方程的标准形式
解 方 程
一元一次方程的应用
方程的解
一、方程的有关概念
1、方程
2、解方程
3、方程的解
4、一元一次方程
方程的两边都整式，只含有一个未知数,并且未知数的指数是一次，这样的方程叫做一元一次方程
下 列方程中,是一元一次方程的是( )
3x=2y
(A)
(B)
(C)
(D)
D
二、等式的性质
1、等式性质1
2、等式性质2
移项：
把方程中的项改变符号后，从方程的一边移到另一边，这种变形叫做移项（transposition of terms)．
　
特别注意：移项要变号
(Ａ)由3x= -2x+5得 3x-2x=5(　　）　
(Ｂ)由7= -x得 x= 7 ( )
(C)由-5x+3=8x-4 得-5x-8x = -4-3( )
(D)由 5= -2x+x 得2x-x=5 ( )　
下列移项变形正确吗？
步 骤
注意事项
去分母
去括号
移 项
合 并
系数化为1
防止漏乘（尤其整数项）注意添括号；
注意变号，不漏乘；
移项要变号，防止漏项；
系数合并，再乘字母
同除以x的系数
三、解方程的一般步骤
一填空题
1、一个数x的2倍减去7的差, 得36 ,列方程为____________；
2、方程5 x – 6 = 0的解是x =________；
3、日历中同一竖列相邻三个数的和为63，则这三个数分别为_____________；
4、 方程去分母得： .
练 习 题
2x-7=36
1.2
14、21、28.
5x-10 = 2x
5、一根长18米的铁丝围成一个长是宽的2倍的
长方形,这个长方形的面积为 ；
6、一件衬衫进货价60元,提高50%后标价,则标
价为 _____, 八折优惠价为______,利润
为______；
18平方米
90元
72元
12元
二、选择题
1、方程 3x －5 = 7＋2 x 移项后得-------------（ ）
A. 3x－2 x = 7－5 ，B. 3x＋2 x = 7－5 ，
C. 3x＋2 x = 7＋5 ，D. 3x－2 x = 7＋5 ；
2、方程 x －a = 7 的解是x =2，则a = --------（ ）
A. 1 ， B. －1 ， C. 5 ， D. －5 ；
3、方程 去分母后可得-----（ ）
A. 3 x－3 =1＋2 x ，B. 3 x－9 =1＋2 x ，
C. 3 x－3 =2＋2 x ，D. 3 x－12=2＋4 x ；
D
D
B
4、日历中同一竖列相邻三个数的和可以是----（ ）
A 78 ， B 26 ， C 21 ， D 45
5、下列不是一元一次方程的是--------------------（ ）
A 4 x－1 = 2 x ， B 3x－2 x = 7 ，
C x－2 = 0 ， D x = y ；
6、某商品提价100%后要恢复原价，则应降价-（ ）
A 30% ， B 50% ， C 75% ， D 100% ；
D
D
B
7、小明每秒钟跑6米，小彬每秒钟跑5米，小彬站在小
明前10米处，两人同时起跑，小明多少秒钟追上
小彬 --------------------------------------------（ ） A 5秒， B 6秒， C 8秒， D 10秒； 8、小山上大学向某商人贷款1万元，月利率为6‰ ，
1年后需还给商人多少钱？-----------------（ ） A 17200元， B 16000元，
C 10720元， D 10600元
D
C
9、方程 是一元一次方程，则a和m分别为-------（ ）
A 2和4 ， B －2 和 4 ，
C 2 和 －4 ， D －2 和－4 。
B
三 解下列方程
1.
解：
合并同类项，得：
移项，得：
方程两边同除以
-1，得：
2.
解：
去括号，得：
移项，得：
合并同类项，得：
方程两边同
除以-1，得：
解、
去分母，得：
去括号，得：
移项，得：
合并同类项，得：
方程两边同
除以-1，得：
3.
去分母，得：
去括号，得：
移项，得：
合并同类项，得：
方程两边同除以13，得：
解：
原方程可化为：
4.
解下列方程:
4
1
3
3
4
)
4
(
-
=
-
x
x
1
3
1
2
4
2
)
5
(
+
-
=
+
y
y
5
.
2
3
1
4
.
0
3
.
0
2
.
0
)
6
(
x
x
-
=
-
-
1.一个两位数,个位数字为a, 十位数字比个位数大3,则这个两位数是___________.
2.若k是方程2x+1=3的解,则4k+3=____________
3. 已知2x-1与-x+5互为相反数，则x=______.
11a+30
7
-4
相信你能行！
4. 已知x=-2是方程ax+x=5(x-a)的 解，求a的 值
列方程解应用题的一般步骤是：
1.审题：分析题意，找出题中的数量关系及其关系；
2.设元：选择一个适当的未知数用字母表示；
3.列方程：根据相等关系列出方程；
4. 解方程：求出未知数的值；
5. 检验：检验求得的值是否正确和符合实际情形，
并写出答案.

顺、逆流问题：
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
顺流路程=逆流路程
工程问题：
工作量=人均效率×人数×时间
利润问题：
利润 = 售价－进价
利润 = 进价×利润率
打 x 折的售价=
原价×
常见的类型
相遇问题：
甲的路程+乙的路程=全程
数字问题：
若一个三位数，百位数字为a,十位数字为b，
个位数字为c，则这个三位数为100a+10b+c
等积变形问题：
变形前的体积=变形后的体积
追及问题：
(同地) 甲的路程=乙的路程
(异地) 甲的路程=乙的路程+原先距离
利息问题：
利息=本金×期数×利率
本息=本金+利息（有时实得利息=利息×80%）
一只船在两个码头之间航行，水流速度是3千米/时，顺水航行需2小时，逆水航行需3小时，求静水速度。
顺、逆流问题
一件工作,甲单独做需要15 天完成,乙单独做需要12天完成,现在甲先单 独做1天,接着乙单独做4天,剩下的工作由甲、乙合做。问合做多少天可以完成全部工作任务？
工程问题
利润问题
为了拓展销路，商店对某种照相机的售价作了调整，按原价的8折出售，此时的利润率为14%，若此种照相机的进价为1200元，问该照相机的原售价是多少元？
相遇问题
甲乙两人骑自行车，同时从相距45千米的两地相向而行，2小时后相遇，已知甲比乙每小时多走2.5千米，求两人每小时各走多少千米？
数字问题
一个三位数满足的条件：①三个数位上的数字和为20；②百位上的数字比十位上的数字大5；③个位上的数字是十位上的数字的3倍。这个三位数是几？
在一只底面直径为30 cm，高为8 cm的圆锥形容器中倒满水，然后将水倒入一只底面直径为10 cm的圆柱形容器里，圆柱形容器中的水有多高？
等积变形问题
追及问题
甲、乙两人练习跑步，从同一地点出发，甲每分钟跑250米，乙每分钟跑200米，甲因找跑鞋比乙晚出发3分钟，结果两人同时到达终点，求两人所跑的路程。
利息问题
某企业在银行存入甲乙两种不同性质用途的存款共20万元，甲种存款年利息为5.5%，乙种存款年利息为4.5%，该企业一年可获利息收入9500元，求甲乙两种存款各多少元？
某部队开展支农活动，甲队27人，乙队19人，现另调26人去支援，使甲队是乙队的2倍，问应调往甲队、乙队各多少人？
解：设调往甲队x人，则调往乙队（26-x)人
根据题意，得方程：
解方程得：x = 21
答：调往甲队21人。调往乙队5人。
人员调配问题
一天，小马虎的爸爸大马虎请客，他看到几个人没来，就自言自语：“怎么该来的不来呢？”客人听了，觉得自己是不该来的，于是有一半客人走了，他一看十分着急，又说“哎，不该走的倒走了！”剩下的人一听 ，是我们该走啊！剩下的人中又有三分之二离开了，他着急地一拍大腿，连说：“我又不是说他们.”于是剩下的3个人也都走了，聪明的你知道开始来了多少客人吗？
解：设开始来了x位客人，可得：
小马虎的解法：
解得：
答：开始来了4人。
客人走后，爸爸大马虎要和儿子小马虎一起把18个客人追回来，他们把任务进行了分配，大马虎负责追一部分，小马虎负责追另一部分客人。可是小马虎抱怨太累了，大马虎训斥道：“你抱怨什么呀？如果你把客人再交一个给我追，那我所追的人数就是你的两倍了，还抱怨什么？”那么大马虎和小马虎各追多少人呢？
还能找到别的等量关系？
为了进一步取得客人的理解，大马虎通过淘宝网购买礼品。已知甲乙两个网店刚好共有某种礼品18个，甲店每个礼品售价50元，而且每个邮费5元；乙店每个礼品售价60元，购买五个以下（包括五个）每个需付邮费5元，购买五个以上的全部邮费只需付25元。下了订单后，共支付了1060元。那么甲乙两个网店各有这种礼品多少个呢？
试一试
1、元旦某公园的成人的门票每张8元，儿童门票半价（即每张4元），全天共售出门票3000张，收入15600元。问这天售出儿童门票多少张？
解：设售出儿童门票x张
根据题意，得：
解方程，得： x = 2100
答：共售出儿童票2100张
从某个日历的日历表中取一个2×2方块.已知这个方块
所围成的4个方格的日期之和为44,求这4个方格中的日期.
3.汽车队运送一批货物，若每辆车装4吨，还剩下8吨未装,若每辆车装4.5吨,恰好装完,这个车队有多少辆车
4.有一架飞机最多能在空中连续飞行8.8小时,它来回的速度分别为920千米/时和840千米/时.这架飞机最远飞行多少千米就应该返回
5.一商店将每台彩电先按进价提高40%标
出售价，然后广告宣传将以80%的优惠价
出售，结果每台赚了300元，则经销这种
产品的利润率是多少？
6.某商店有两种不同型号计算器的出售价都是64元，卖出其中一种计算器商店盈利为进货价的60％，卖出另一种商店亏损为进价的20％。若卖出这两种计算器各1台，这家商店的盈亏情况如何？
7. 水源透支令人担忧，节约用水迫在眉睫
针对居民用水浪费现象，北京市将制定居民
用水标准，规定三口之家楼房每月标准用水
量，超标部分加价收费，假设不超标部分每
立方米水费1.3元，超标部分每立方米水费
2.9元，某住楼房的三口之家七月份用水12
立方米，交水费22元
（1）请你通过列方程求出北京市规定的三
口之家楼房每月标准用水量为多少立方米？
（2）若某住楼房的三口之家每月用水a立方
米，应交水费为b元，用含a的代数式表示b
8. 某国家规定工资收入的个人所得
税计算方法是：
（1）月收入不超过1200元的部分不
纳税
（2）收入超过1200元至1700元的部分
按税率5%征税
（3）收入超过1700元至3000元的部分
按税率10%征税……
已知某人本月缴纳个人所得税65元，
问此人本月收入多少元？
9.今年父亲的年龄是儿子年龄的3倍，5年前父亲的年龄是儿子年龄的4倍，问今年父亲，儿子各几岁？
提高题
按图示的方法搭1个三角形需要3根火柴棒，搭2个三角形需要5根火柴棒。设共搭成n个三角形，你怎样用关于n的代数式表示n个三角形需要火柴棒的根数？现有2009根火柴棒，能搭几个这样的三角形？2100根呢？
3
5
7
9
1
2
3
4
n
2n+1
谈谈你本节课的收获。
信心、细心、耐心
随时留意、全心全意