2020-2021学年浙教 版八年级下册数学 第5章 特殊平行四边形 单元测试卷(word版含答案)
文档属性
| 名称 | 2020-2021学年浙教 版八年级下册数学 第5章 特殊平行四边形 单元测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 22:45:21 | ||
图片预览

文档简介
2020-2021学年浙教新版八年级下册数学《第5章 特殊平行四边形》单元测试卷
一.选择题
1.已知矩形的两条对角线的夹角为60°,两条对角线的和为8,则矩形的周长为( )
A.2+4 B. C. D.
2.已知,在等腰△ABC中,AB=AC,分别延长BA,CA到D,E点,使DA=AB,EA=CA,则四边形BCDE是( )
A.任意四边形 B.矩形 C.菱形 D.正方形
3.如图,AC,BD是菱形ABCD的对角线,且交于点O,则下面正确的是( )
A.图中共有五个三角形,它们不全等
B.图中只有四个全等的直角三角形
C.图中有四对全等直角三角形
D.图中有四个全等的直角三角形,两对全等的等腰三角形
4.用折纸、剪切的方法得到一个菱形,最少要剪( )刀(设一条线段剪一刀).
A.1 B.2 C.3 D.4
5.顺次连接下列各图形的中点,构成的图形一定是正方形的为( )
A.平行四边形
B.矩形
C.菱形
D.对角线互相垂直的等腰梯形
6.如图所示,沿正方形对角线对折、互相重合的两个小正方形内的数字的乘积等于( )
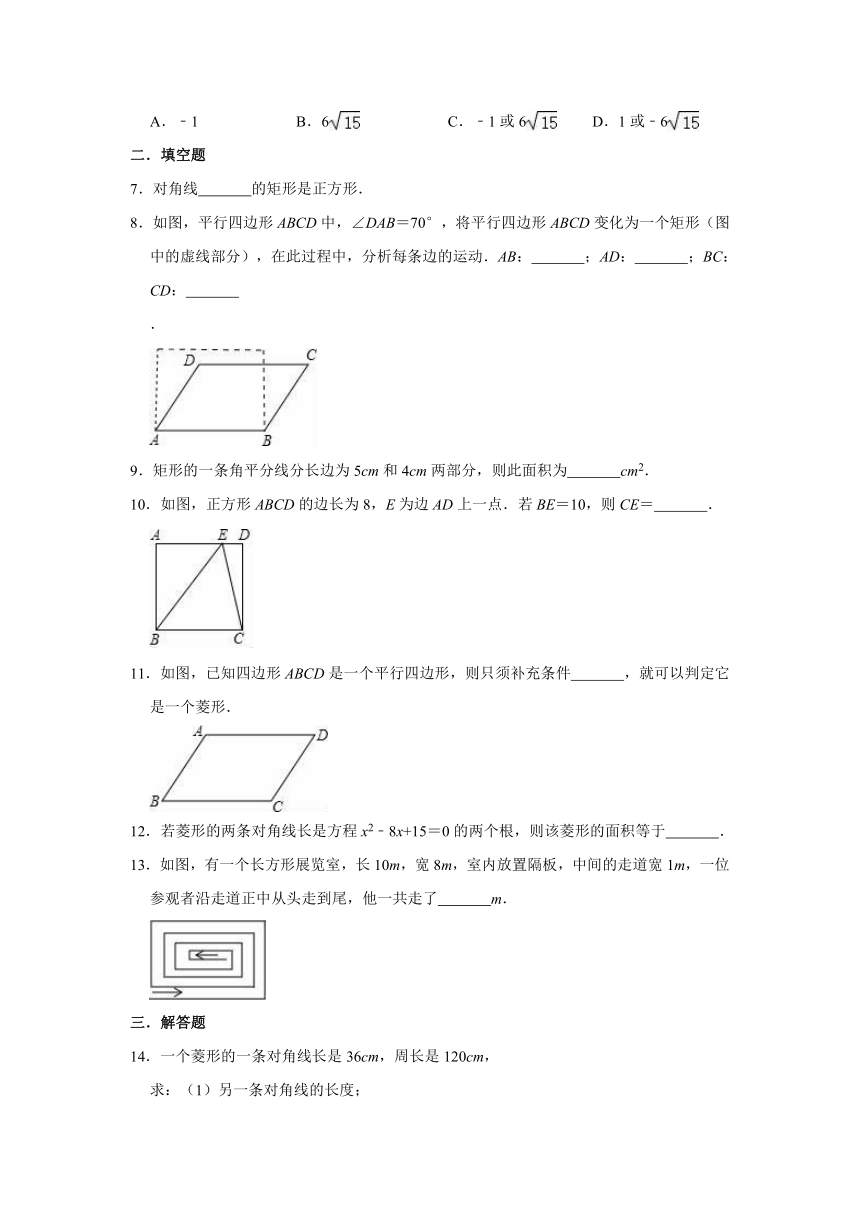
A.﹣1 B.6 C.﹣1或6 D.1或﹣6
二.填空题
7.对角线 的矩形是正方形.
8.如图,平行四边形ABCD中,∠DAB=70°,将平行四边形ABCD变化为一个矩形(图中的虚线部分),在此过程中,分析每条边的运动.AB: ;AD: ;BC: CD:
.
9.矩形的一条角平分线分长边为5cm和4cm两部分,则此面积为 cm2.
10.如图,正方形ABCD的边长为8,E为边AD上一点.若BE=10,则CE= .
11.如图,已知四边形ABCD是一个平行四边形,则只须补充条件 ,就可以判定它是一个菱形.
12.若菱形的两条对角线长是方程x2﹣8x+15=0的两个根,则该菱形的面积等于 .
13.如图,有一个长方形展览室,长10m,宽8m,室内放置隔板,中间的走道宽1m,一位参观者沿走道正中从头走到尾,他一共走了 m.
三.解答题
14.一个菱形的一条对角线长是36cm,周长是120cm,
求:(1)另一条对角线的长度;
(2)这个菱形的面积.
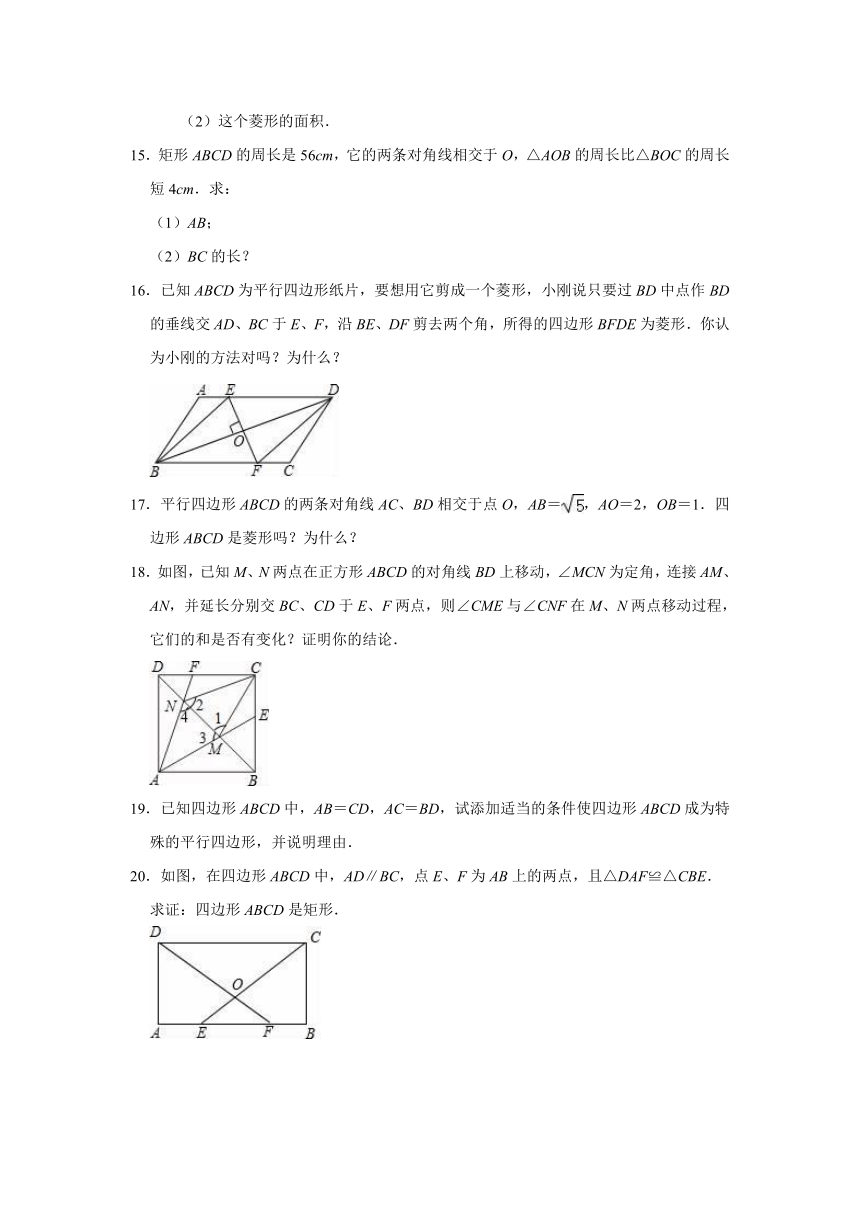
15.矩形ABCD的周长是56cm,它的两条对角线相交于O,△AOB的周长比△BOC的周长短4cm.求:
(1)AB;
(2)BC的长?
16.已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?
17.平行四边形ABCD的两条对角线AC、BD相交于点O,AB=,AO=2,OB=1.四边形ABCD是菱形吗?为什么?
18.如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
19.已知四边形ABCD中,AB=CD,AC=BD,试添加适当的条件使四边形ABCD成为特殊的平行四边形,并说明理由.
20.如图,在四边形ABCD中,AD∥BC,点E、F为AB上的两点,且△DAF≌△CBE.
求证:四边形ABCD是矩形.
参考答案与试题解析
一.选择题
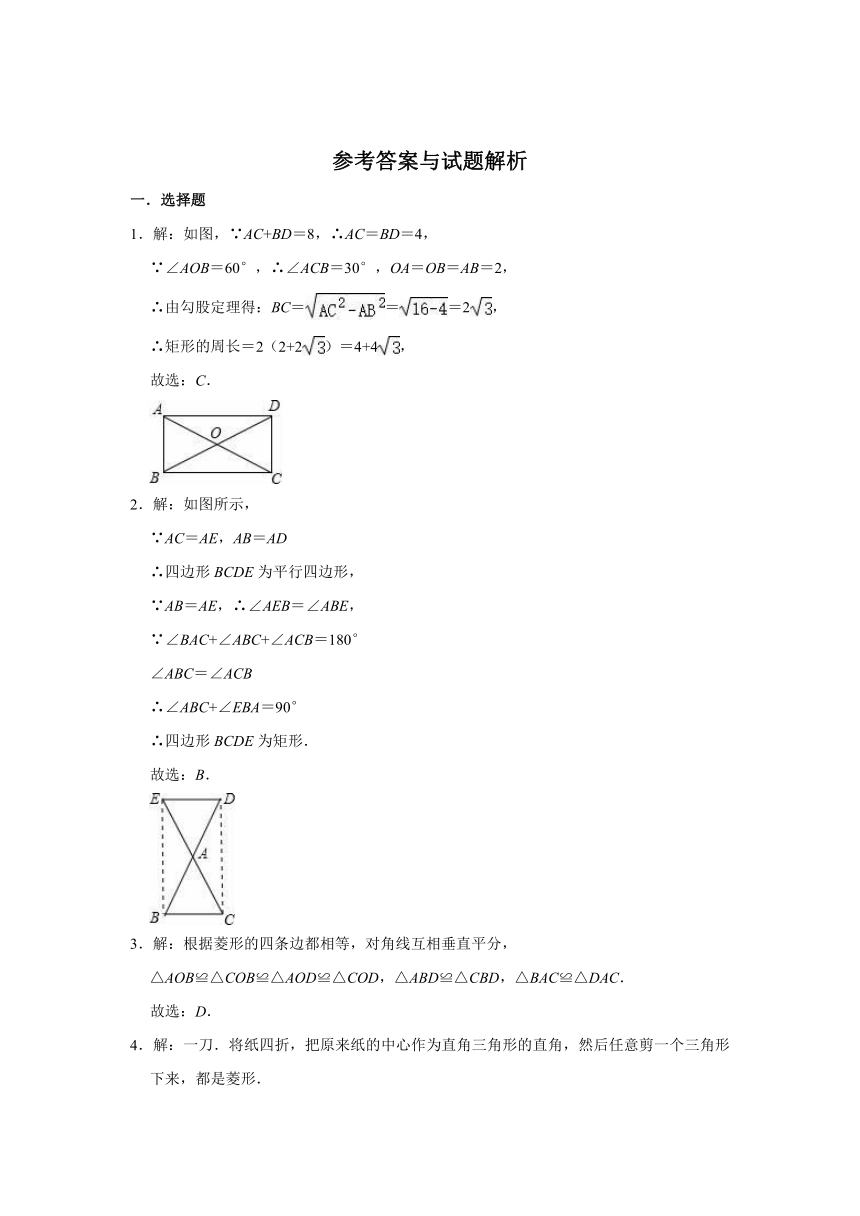
1.解:如图,∵AC+BD=8,∴AC=BD=4,
∵∠AOB=60°,∴∠ACB=30°,OA=OB=AB=2,
∴由勾股定理得:BC===2,
∴矩形的周长=2(2+2)=4+4,
故选:C.
2.解:如图所示,
∵AC=AE,AB=AD
∴四边形BCDE为平行四边形,
∵AB=AE,∴∠AEB=∠ABE,
∵∠BAC+∠ABC+∠ACB=180°
∠ABC=∠ACB
∴∠ABC+∠EBA=90°
∴四边形BCDE为矩形.
故选:B.
3.解:根据菱形的四条边都相等,对角线互相垂直平分,
△AOB≌△COB≌△AOD≌△COD,△ABD≌△CBD,△BAC≌△DAC.
故选:D.
4.解:一刀.将纸四折,把原来纸的中心作为直角三角形的直角,然后任意剪一个三角形下来,都是菱形.
故选:A.
5.解:顺次连接下列各图形的中点,构成的四边形的两组对边分别平行于原图形的对角线,且每组边等于相对的对角线的一半,可判定为平行四边形,当原图形的对角线互相垂直时,又可判定为菱形,而等腰梯形的对角线相等,所以可判定为正方形,故选D.
6.解:沿正方形对角线对折、互相重合的两个小正方形内的数字分别是3和2,1+和1﹣,可得其乘积分别等于﹣1或6;故选C.
二.填空题
7.解:对角线互相垂直的矩形是正方形.故答案为:互相垂直.
8.解:不动;绕点A沿逆时针旋转20°;
绕点B沿逆时针旋转20°;平移.
9.解:(1)矩形的长为5+4=9cm,
根据矩形的性质可得宽为5cm时,矩形面积为9×5=45cm2;
(2)当宽为4cm时,则矩形面积为9×4=36cm2.
10.解:∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=CD=AD=8,
∴AE===6,
∴DE=AD﹣AE=2,
∴CE===2;
故答案为:2.
11.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
12.解:∵x2﹣8x+15=0
x=3或x=5.
所以菱形的面积为:(3×5)÷2=7.5.
故答案为:7.5.
13.解:参观者在第一个隔板内走的路程是10﹣0.5,在最上边的隔板走的路程是10﹣1=9mm,在下面第二个横道的路长是10﹣1﹣1=8m,再在上面第二个横道的路程是8﹣1=7m.依此类推,就可以求出所有在横道内走的路程,同样可以求出在所有纵路内所走的路程,把各个数相加就可以得到总路程.
答:他一共走了80m.
故答案为:80.
三.解答题
14.解:(1)由题意得,AC=36cm,四边形ABCD的周长为120cm,
∵四边形ABCD是菱形,
∴AB=30cm,AO=AC=18cm,
在RT△ABO中,BO==24cm,
故BD=2BO=48cm.
(2)这个菱形的面积=AC×BD=864cm2.
15.解:矩形ABCD中,OA=OC,
∵△AOB的周长比△BOC的周长短4cm,
∴(OB+OC+BC)﹣(OB+OA+AB)=4,
即BC﹣AB=4,
所以,BC=AB+4①,
矩形ABCD的周长=2(AB+BC)=56,
所以,AB+BC=28②,
①代入②得,AB+AB+4=28,
解得AB=12cm,
BC=AB+4=12+4=16cm,
所以,(1)AB=12cm;
(2)BC的长为16cm.
16.解:小刚的方法对;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EDO=∠FBO,∠DEO=∠BFO,
∵O是BD的中点,
∴OD=OB,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(AAS),
∴DE=BF,
∴四边形BFDE是平行四边形,
又∵EF⊥BD,
∴四边形BFDE为菱形.
17.解:在△AOB中,
∵AB=,AO=2,OB=1,
∴AB2=()2=5,AO2+OB2=22+12=5,
∴AB2=AO2+OB2,
∴△AOB为直角三角形,即∠AOB=90°.
∴AC、BD互相垂直.
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
18.解:∵BD为正方形ABCD的对角线,
∴∠1=∠3,∠2=∠4,
∴∠EMC=180°﹣∠1﹣∠3=180°﹣2∠1.
同理∠FNC=180°﹣2∠2.
∴∠EMC+∠FNC=360°﹣2(∠1+∠2).
∵∠MCN=180°﹣(∠1+∠2),
∴∠EMC+∠FNC总与2∠MCN相等.
因此∠EMC+∠FNC始终为定角,这定角为∠MCN的2倍.
19.解:本题答案不唯一,以下是其中两种解法:
(1)添加条件AB∥DC,可得出该四边形是矩形;
理由:∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形.
∵AC=BD,
∴四边形ABCD是矩形.
(2)添加条件AC垂直平分BD,那么该四边形是正方形.
理由:∵AC垂直平分BD,
∴AB=AD,BC=CD.
∵AB=DC,
∴AB=AD=BC=DC.
∴四边形ABCD是菱形.
∵AC平分BD,
∴四边形ABCD是正方形.
20.证明:∵AD∥BC,
∴∠A+∠B=180°,
∵△DAF≌△CBE,
∴∠A=∠B,AD=BC,
∴∠A=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
一.选择题
1.已知矩形的两条对角线的夹角为60°,两条对角线的和为8,则矩形的周长为( )
A.2+4 B. C. D.
2.已知,在等腰△ABC中,AB=AC,分别延长BA,CA到D,E点,使DA=AB,EA=CA,则四边形BCDE是( )
A.任意四边形 B.矩形 C.菱形 D.正方形
3.如图,AC,BD是菱形ABCD的对角线,且交于点O,则下面正确的是( )
A.图中共有五个三角形,它们不全等
B.图中只有四个全等的直角三角形
C.图中有四对全等直角三角形
D.图中有四个全等的直角三角形,两对全等的等腰三角形
4.用折纸、剪切的方法得到一个菱形,最少要剪( )刀(设一条线段剪一刀).
A.1 B.2 C.3 D.4
5.顺次连接下列各图形的中点,构成的图形一定是正方形的为( )
A.平行四边形
B.矩形
C.菱形
D.对角线互相垂直的等腰梯形
6.如图所示,沿正方形对角线对折、互相重合的两个小正方形内的数字的乘积等于( )
A.﹣1 B.6 C.﹣1或6 D.1或﹣6
二.填空题
7.对角线 的矩形是正方形.
8.如图,平行四边形ABCD中,∠DAB=70°,将平行四边形ABCD变化为一个矩形(图中的虚线部分),在此过程中,分析每条边的运动.AB: ;AD: ;BC: CD:
.
9.矩形的一条角平分线分长边为5cm和4cm两部分,则此面积为 cm2.
10.如图,正方形ABCD的边长为8,E为边AD上一点.若BE=10,则CE= .
11.如图,已知四边形ABCD是一个平行四边形,则只须补充条件 ,就可以判定它是一个菱形.
12.若菱形的两条对角线长是方程x2﹣8x+15=0的两个根,则该菱形的面积等于 .
13.如图,有一个长方形展览室,长10m,宽8m,室内放置隔板,中间的走道宽1m,一位参观者沿走道正中从头走到尾,他一共走了 m.
三.解答题
14.一个菱形的一条对角线长是36cm,周长是120cm,
求:(1)另一条对角线的长度;
(2)这个菱形的面积.
15.矩形ABCD的周长是56cm,它的两条对角线相交于O,△AOB的周长比△BOC的周长短4cm.求:
(1)AB;
(2)BC的长?
16.已知ABCD为平行四边形纸片,要想用它剪成一个菱形,小刚说只要过BD中点作BD的垂线交AD、BC于E、F,沿BE、DF剪去两个角,所得的四边形BFDE为菱形.你认为小刚的方法对吗?为什么?
17.平行四边形ABCD的两条对角线AC、BD相交于点O,AB=,AO=2,OB=1.四边形ABCD是菱形吗?为什么?
18.如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
19.已知四边形ABCD中,AB=CD,AC=BD,试添加适当的条件使四边形ABCD成为特殊的平行四边形,并说明理由.
20.如图,在四边形ABCD中,AD∥BC,点E、F为AB上的两点,且△DAF≌△CBE.
求证:四边形ABCD是矩形.
参考答案与试题解析
一.选择题
1.解:如图,∵AC+BD=8,∴AC=BD=4,
∵∠AOB=60°,∴∠ACB=30°,OA=OB=AB=2,
∴由勾股定理得:BC===2,
∴矩形的周长=2(2+2)=4+4,
故选:C.
2.解:如图所示,
∵AC=AE,AB=AD
∴四边形BCDE为平行四边形,
∵AB=AE,∴∠AEB=∠ABE,
∵∠BAC+∠ABC+∠ACB=180°
∠ABC=∠ACB
∴∠ABC+∠EBA=90°
∴四边形BCDE为矩形.
故选:B.
3.解:根据菱形的四条边都相等,对角线互相垂直平分,
△AOB≌△COB≌△AOD≌△COD,△ABD≌△CBD,△BAC≌△DAC.
故选:D.
4.解:一刀.将纸四折,把原来纸的中心作为直角三角形的直角,然后任意剪一个三角形下来,都是菱形.
故选:A.
5.解:顺次连接下列各图形的中点,构成的四边形的两组对边分别平行于原图形的对角线,且每组边等于相对的对角线的一半,可判定为平行四边形,当原图形的对角线互相垂直时,又可判定为菱形,而等腰梯形的对角线相等,所以可判定为正方形,故选D.
6.解:沿正方形对角线对折、互相重合的两个小正方形内的数字分别是3和2,1+和1﹣,可得其乘积分别等于﹣1或6;故选C.
二.填空题
7.解:对角线互相垂直的矩形是正方形.故答案为:互相垂直.
8.解:不动;绕点A沿逆时针旋转20°;
绕点B沿逆时针旋转20°;平移.
9.解:(1)矩形的长为5+4=9cm,
根据矩形的性质可得宽为5cm时,矩形面积为9×5=45cm2;
(2)当宽为4cm时,则矩形面积为9×4=36cm2.
10.解:∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=CD=AD=8,
∴AE===6,
∴DE=AD﹣AE=2,
∴CE===2;
故答案为:2.
11.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
12.解:∵x2﹣8x+15=0
x=3或x=5.
所以菱形的面积为:(3×5)÷2=7.5.
故答案为:7.5.
13.解:参观者在第一个隔板内走的路程是10﹣0.5,在最上边的隔板走的路程是10﹣1=9mm,在下面第二个横道的路长是10﹣1﹣1=8m,再在上面第二个横道的路程是8﹣1=7m.依此类推,就可以求出所有在横道内走的路程,同样可以求出在所有纵路内所走的路程,把各个数相加就可以得到总路程.
答:他一共走了80m.
故答案为:80.
三.解答题
14.解:(1)由题意得,AC=36cm,四边形ABCD的周长为120cm,
∵四边形ABCD是菱形,
∴AB=30cm,AO=AC=18cm,
在RT△ABO中,BO==24cm,
故BD=2BO=48cm.
(2)这个菱形的面积=AC×BD=864cm2.
15.解:矩形ABCD中,OA=OC,
∵△AOB的周长比△BOC的周长短4cm,
∴(OB+OC+BC)﹣(OB+OA+AB)=4,
即BC﹣AB=4,
所以,BC=AB+4①,
矩形ABCD的周长=2(AB+BC)=56,
所以,AB+BC=28②,
①代入②得,AB+AB+4=28,
解得AB=12cm,
BC=AB+4=12+4=16cm,
所以,(1)AB=12cm;
(2)BC的长为16cm.
16.解:小刚的方法对;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EDO=∠FBO,∠DEO=∠BFO,
∵O是BD的中点,
∴OD=OB,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(AAS),
∴DE=BF,
∴四边形BFDE是平行四边形,
又∵EF⊥BD,
∴四边形BFDE为菱形.
17.解:在△AOB中,
∵AB=,AO=2,OB=1,
∴AB2=()2=5,AO2+OB2=22+12=5,
∴AB2=AO2+OB2,
∴△AOB为直角三角形,即∠AOB=90°.
∴AC、BD互相垂直.
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
18.解:∵BD为正方形ABCD的对角线,
∴∠1=∠3,∠2=∠4,
∴∠EMC=180°﹣∠1﹣∠3=180°﹣2∠1.
同理∠FNC=180°﹣2∠2.
∴∠EMC+∠FNC=360°﹣2(∠1+∠2).
∵∠MCN=180°﹣(∠1+∠2),
∴∠EMC+∠FNC总与2∠MCN相等.
因此∠EMC+∠FNC始终为定角,这定角为∠MCN的2倍.
19.解:本题答案不唯一,以下是其中两种解法:
(1)添加条件AB∥DC,可得出该四边形是矩形;
理由:∵AB∥DC,AB=DC,
∴四边形ABCD是平行四边形.
∵AC=BD,
∴四边形ABCD是矩形.
(2)添加条件AC垂直平分BD,那么该四边形是正方形.
理由:∵AC垂直平分BD,
∴AB=AD,BC=CD.
∵AB=DC,
∴AB=AD=BC=DC.
∴四边形ABCD是菱形.
∵AC平分BD,
∴四边形ABCD是正方形.
20.证明:∵AD∥BC,
∴∠A+∠B=180°,
∵△DAF≌△CBE,
∴∠A=∠B,AD=BC,
∴∠A=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
