浙教版数学八年级下册第2章《一元二次方程》复习课件(27张PPT)
文档属性
| 名称 | 浙教版数学八年级下册第2章《一元二次方程》复习课件(27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 604.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 18:54:27 | ||
图片预览








文档简介
(共27张PPT)
(1)两边都是整式;
(2)只含有一个未知数;
(3)未知数最高次数为2次
具有以上三个特点的方程称为一元二次方程
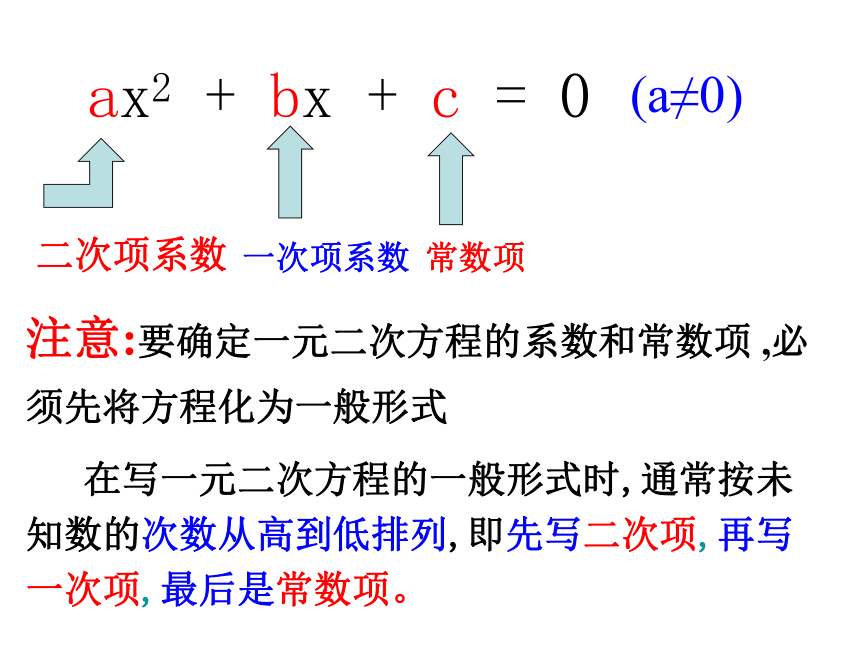
我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式.
ax2 + bx + c = 0
注意:要确定一元二次方程的系数和常数项 ,必须先将方程化为一般形式
二次项系数
一次项系数
常数项
(a≠0)
在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
判断下列方程是一元二次方程吗
√
√
√
√
√
例1、把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.
1.关于x的方程 (k-3)x2 + 2x-1=0,当 k _______时,是一元二次方程.
2.关于x的方程 (k2-1)x2 + 2 (k-1) x + 2k+ 2=0, 当k 时,是一元二次方程;
当 k 时,是一元一次方程.
≠3
≠±1
=-1
做一做
构造一个一元二次方程,要求:
(1)常数项为零;(2)有一根为2。
一元二次方程的解:能使一元二次方程两边相等的未知数的值叫一元二次方程的解或根。
一元二次方程的解法
1、因式分解法
2、直接开平方法
3、先配方再开平方法
4、公式法
1、因式分解法
原理:
若A·B=0,则A=0或B=0
①提取公因式
②乘法公式
③十字相乘
做一做:
(1)
(3)
(4)
(2)
(5)
2、直接开平方法
一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
用开平方法解下列方程:
(1)3x2-48=0; (2)(x-5)2=9
(3)(2x-3)2=7
3、先配方再开平方法
对于形如x2+ax+b=0的方程,不能
因式分解。用配方法
加上一次项系数一半的平方
(1)x2+6x=1
(2)x2=6-5x
(3)x2+13=12x
步骤?
(2)开平方法
(3)配方法+开平方法
(1)因式分解法
一元二次方程的解法:
若A·B=0,则A=0或B=0
x2=a(a≥0)
x2+bx+c=0
加上一次项系数一半的平方
(1) 2x2+4x-3=0 (2) 3x2-8x-3=0
★一除、二移、三配、四开、五解.
完善“配方法”解方程的基本步骤:
例7 已知 是一个关于x的完全平方式,求常数n的值。
你能用配方法解一般形式的一元二次方程ax2+bx+c=0(a≠0)吗?
用配方法解一般形式的一元二次方程
把方程两边都除以
解:
移项,得
配方,得
即
此类方程一定有实数根么?
必须符合什么条件?
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
一般地,对于一元二次方程 ,
如果 , 那么两个根为
这个公式叫做一元二次方程的求根公式.利用求根公式,我们可以 由一元二次方程的系数 的值,直接求得方程的根.这种解一元二次方程的方法叫做公式法.
1、把方程化成一般形式,并写出a,b,c的值.
4、写出方程的解x1与x2.
2、求出b2-4ac的值.
3、代入求根公式 :
用公式法解一元二次方程的步骤:
一元二次方程根与系数的关系是
法国数学家“韦达”发现的,所以我们又
称之为韦达定理.
说出下列各方程的两根之和与两根之积:
(1) x2 - 2x - 1=0
(3) 2x2 - 6x =0
(4) 3x2 = 4
(2) 2x2 - 3x + =0
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2=
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.
解法一:
设方程的另一个根为x2.
由根与系数的关系,得
2 + x2 = k+1
2 x2 = 3k
解这方程组,得
x2 =-3
k =-2
答:方程的另一个根是-3 , k的值是-2.
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解法二:
设方程的另一个根为x2.
把x=2代入方程,得 4-2(k+1)+3k=0
解这方程,得 k= - 2
由根与系数的关系,得2 x2=3k
即2 x2=-6
∴ x2 =-3
答:方程的另一个根是-3 , k的值是-2.
例2、方程2x2-3x+1=0的两根记作x1,x2,
不解方程,求:
(1) ; (2) ;
; (4) .
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
{
{
{
(1)两边都是整式;
(2)只含有一个未知数;
(3)未知数最高次数为2次
具有以上三个特点的方程称为一元二次方程
我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式.
ax2 + bx + c = 0
注意:要确定一元二次方程的系数和常数项 ,必须先将方程化为一般形式
二次项系数
一次项系数
常数项
(a≠0)
在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
判断下列方程是一元二次方程吗
√
√
√
√
√
例1、把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.
1.关于x的方程 (k-3)x2 + 2x-1=0,当 k _______时,是一元二次方程.
2.关于x的方程 (k2-1)x2 + 2 (k-1) x + 2k+ 2=0, 当k 时,是一元二次方程;
当 k 时,是一元一次方程.
≠3
≠±1
=-1
做一做
构造一个一元二次方程,要求:
(1)常数项为零;(2)有一根为2。
一元二次方程的解:能使一元二次方程两边相等的未知数的值叫一元二次方程的解或根。
一元二次方程的解法
1、因式分解法
2、直接开平方法
3、先配方再开平方法
4、公式法
1、因式分解法
原理:
若A·B=0,则A=0或B=0
①提取公因式
②乘法公式
③十字相乘
做一做:
(1)
(3)
(4)
(2)
(5)
2、直接开平方法
一般地,对于形如x2=a(a≥0)的方程,
根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
用开平方法解下列方程:
(1)3x2-48=0; (2)(x-5)2=9
(3)(2x-3)2=7
3、先配方再开平方法
对于形如x2+ax+b=0的方程,不能
因式分解。用配方法
加上一次项系数一半的平方
(1)x2+6x=1
(2)x2=6-5x
(3)x2+13=12x
步骤?
(2)开平方法
(3)配方法+开平方法
(1)因式分解法
一元二次方程的解法:
若A·B=0,则A=0或B=0
x2=a(a≥0)
x2+bx+c=0
加上一次项系数一半的平方
(1) 2x2+4x-3=0 (2) 3x2-8x-3=0
★一除、二移、三配、四开、五解.
完善“配方法”解方程的基本步骤:
例7 已知 是一个关于x的完全平方式,求常数n的值。
你能用配方法解一般形式的一元二次方程ax2+bx+c=0(a≠0)吗?
用配方法解一般形式的一元二次方程
把方程两边都除以
解:
移项,得
配方,得
即
此类方程一定有实数根么?
必须符合什么条件?
当 时,方程有两个不相等的实数根;
当 时,方程有两个相等的实数根;
当 时,方程没有实数根.
一般地,对于一元二次方程 ,
如果 , 那么两个根为
这个公式叫做一元二次方程的求根公式.利用求根公式,我们可以 由一元二次方程的系数 的值,直接求得方程的根.这种解一元二次方程的方法叫做公式法.
1、把方程化成一般形式,并写出a,b,c的值.
4、写出方程的解x1与x2.
2、求出b2-4ac的值.
3、代入求根公式 :
用公式法解一元二次方程的步骤:
一元二次方程根与系数的关系是
法国数学家“韦达”发现的,所以我们又
称之为韦达定理.
说出下列各方程的两根之和与两根之积:
(1) x2 - 2x - 1=0
(3) 2x2 - 6x =0
(4) 3x2 = 4
(2) 2x2 - 3x + =0
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2=
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.
解法一:
设方程的另一个根为x2.
由根与系数的关系,得
2 + x2 = k+1
2 x2 = 3k
解这方程组,得
x2 =-3
k =-2
答:方程的另一个根是-3 , k的值是-2.
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解法二:
设方程的另一个根为x2.
把x=2代入方程,得 4-2(k+1)+3k=0
解这方程,得 k= - 2
由根与系数的关系,得2 x2=3k
即2 x2=-6
∴ x2 =-3
答:方程的另一个根是-3 , k的值是-2.
例2、方程2x2-3x+1=0的两根记作x1,x2,
不解方程,求:
(1) ; (2) ;
; (4) .
一正根,一负根
△>0
X1X2<0
两个正根
△≥0
X1X2>0
X1+X2>0
两个负根
△≥0
X1X2>0
X1+X2<0
{
{
{
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
