第2章 直线与圆的位置关系 单元测试卷三(含解析)
文档属性
| 名称 | 第2章 直线与圆的位置关系 单元测试卷三(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 498.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 15:09:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九年级数学下册单元测试卷
第二章 直线与圆的位置关系
姓名:___________班级:___________学号:___________
一、选择题(本大题共10小题,共30.0分)
如图,正六边形ABCDEF内接于,若直线PA与相切于点A,则
A.
B.
C.
D.
已知直线l:与以原点O为圆心,5为半径的相交,则b的取值范围为
A. B.
C. D. 或
在平面直角坐标系中,以点为圆心,半径为3的圆一定
A. 与x轴相切,与y轴相切 B. 与x轴相切,与y轴相交
C. 与x轴相交,与y轴相切 D. 与x轴相交,与y轴相交
下列事件中,三点确定一个圆;平分弦的直径垂直于弦;从圆外一点可以引圆的两条切线,它们的切线长相等;关于x的一元二次方程有实数根,则a的取值范围是;圆心角是圆周角的2倍。其中必然事件的个数有
A. 1 B. 2 C. 3 D. 4
如图,AB为半圆O的直径,AD、BC分别切于A,B两点,CD切于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,,则四边形ABCD的周长为
A. B.
C. D.
已知,如图,四边形ABCD内接于,AB为的直径,MN切于C,,则的度数为
A. B.
C. D.
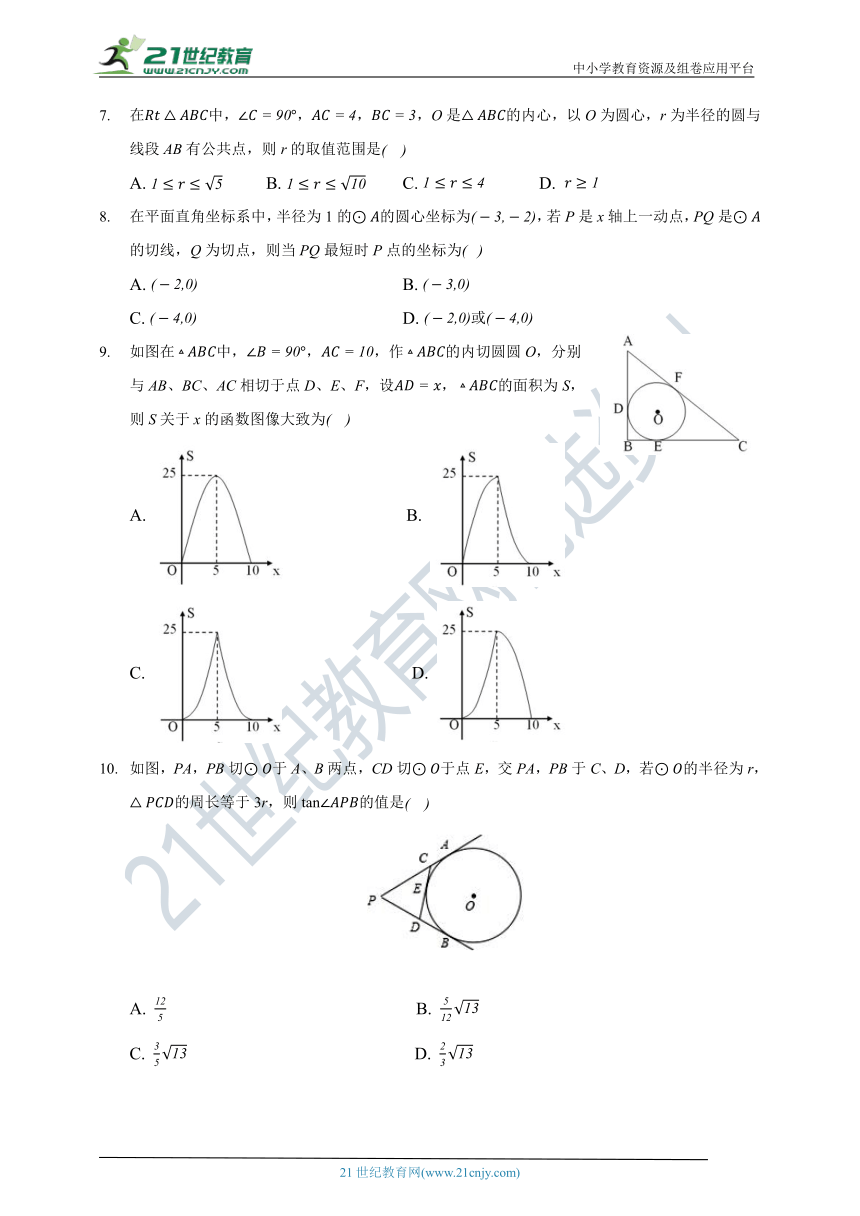
在中,,,,O是的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是
A. B. C. D.
在平面直角坐标系中,半径为1的的圆心坐标为,若P是x轴上一动点,PQ是的切线,Q为切点,则当PQ最短时P点的坐标为
A. B.
C. D. 或
如图在中,,,作的内切圆圆O,分别与AB、BC、AC相切于点D、E、F,设,的面积为S,则S关于x的函数图像大致为
A. B.
C. D.
如图,PA,PB切于A、B两点,CD切于点E,交PA,PB于C、D,若的半径为r,的周长等于3r,则的值是
A. B.
C. D.
二、填空题(本大题共8小题,共24.0分)
在矩形ABCD中,,点O为对角线AC上一点不与A重合,是以点O为圆心,AO为半径的圆当与矩形各边的交点个数为5个时,半径OA的范围是________.
如图,在平面直角坐标系中,函数的图象被截得的弦AB的长为,与y轴相切,半径为3,圆心P位于第一象限内且在直线的上方,则点P坐标是________.
P是的内心,,,则的外接圆半径为_______.
如图,PA、PB是的切线,A、B为切点,点C、D在上.若,则________.
已知在ABC中,C,ABC,若点O为ABC的内心,则OAC______.
将正方形ABCD绕点A按逆时针方向旋转,得正方形,交CD于点E,,则四边形的内切圆半径为__________。
如图,直线交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作,当与直线AB相切时,点P的坐标是______.
如图,等边中,P为三角形内一点,过P作,,,连结AP、BP、CP,如果,那么的内切圆半径为_________.
三、解答题(本大题共6小题,共46.0分)
如图,AB是半圆O的直径,AD为弦,.
求证:BC是半圆O的切线;
若,OC交BD于E,,,求AD的长.
已知正方形ABCD的边长为2,M是BC的中点,P是线段MC上的一个动点,点P不与点M,C重合,以AB为直径作,过点P作的切线交AD于点F,切点为求四边形CDFP的周长.
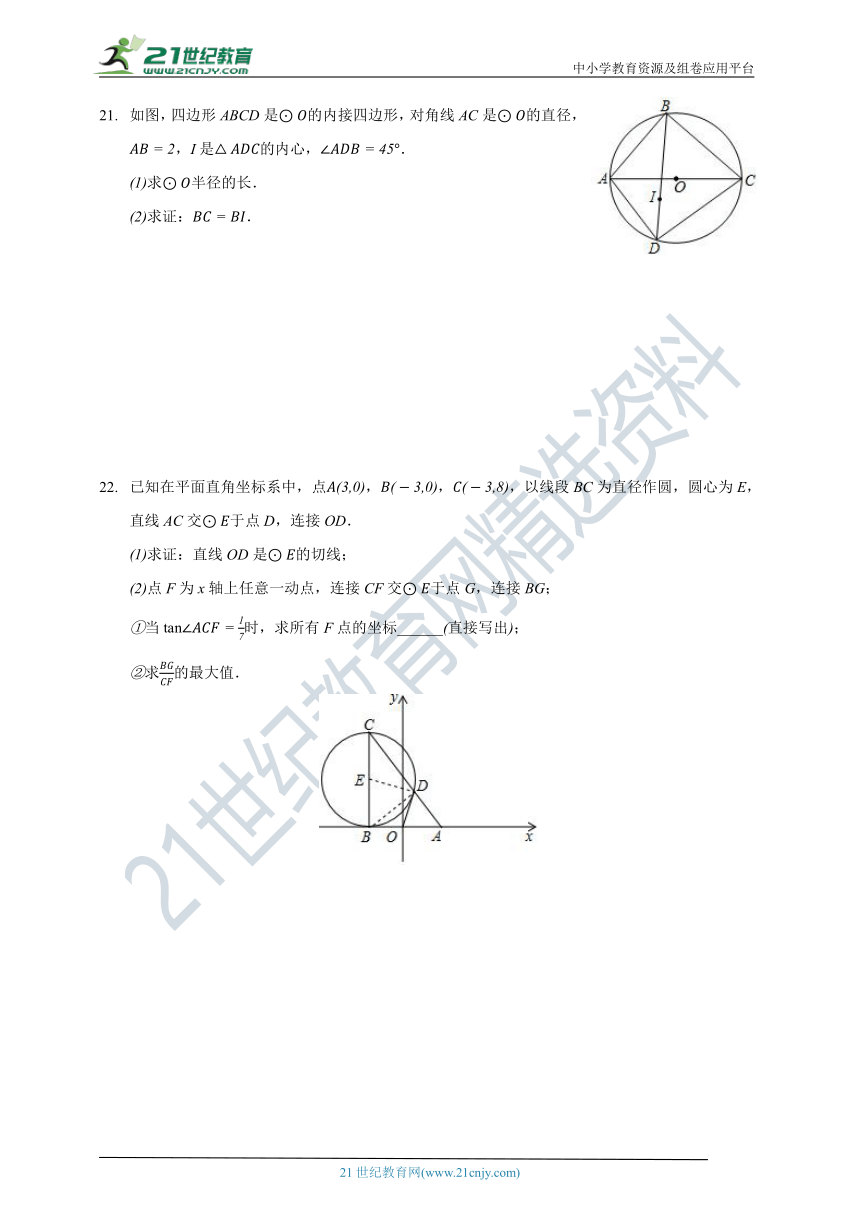
如图,四边形ABCD是的内接四边形,对角线AC是的直径,,I是的内心,.
求半径的长.
求证:.
已知在平面直角坐标系中,点,,,以线段BC为直径作圆,圆心为E,直线AC交于点D,连接OD.
求证:直线OD是的切线;
点F为x轴上任意一动点,连接CF交于点G,连接BG;
当时,求所有F点的坐标______直接写出;
求的最大值.
如图所示,在平面内,给定不在同一直线上的点A,B,C,射线BP是的平分线,点O到点A,B,C的距离均等于为常数,到点O的距离等于a的所有点组成图形G,图形G交射线BP于点D,连接AD,CD.
求证:;
过点D作直线AB的垂线DE,垂足为E,作于点F,延长DF交图形G于点M,连接若,求直线DE与图形G的公共点个数.
阅读材料:
已知,如图,在面积为S的中,,,,内切圆O的半径为连接OA、OB、OC,被划分为三个小三角形.
.
.
类比推理:若面积为S的四边形ABCD存在内切圆与各边都相切的圆,如图,各边长分别为,,,,求四边形的内切圆半径r;
理解应用:如图,在等腰梯形ABCD中,,,,,与分别为与的内切圆,设它们的半径分别为和,求的值.
答案和解析
1.【答案】A
解:连接OB,AD,BD,
多边形ABCDEF是正多边形,
为外接圆的直径,
,
.
直线PA与相切于点A,
,
故选:A.
2.【答案】C
解:如图,假设直线:交x轴与A,交y轴与B,
则:,
,
假设直线:与圆相切,切点是C,
则, .
,
,
.
直线l:与相交时b的取值范围为
.
故选:C
3.【答案】B
解:点到x轴的距离是3,等于半径,
到y轴的距离是2,小于半径,
圆与y轴相交,与x轴相切.
故选B.
4.【答案】A
略
5.【答案】D
解:过D作于F,则,
、BC分别切于A、B两点,CD切于点E,
,,,
四边形ADFB是矩形,
,,
,,,,
,,
,,
在中,由勾股定理得:,
即,
即四边形ABCD的周长是,
故选D.
6.【答案】B
略
7.【答案】B
解:如图,作于D,于E,于F,连接OA、OB,
则四边形OECF是正方形,
,
,,,
,
是的内心,
,
,,
,,
当时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当时,以O为圆心,r为半径的圆与线段AB有两个交点;
当时,以O为圆心,r为半径的圆与线段AB有1个交点;
以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是;
故选B
8.【答案】B
解:连接AQ,AP,如图,
根据切线的性质定理,得,
要使PQ最小,只需AP最小,
则根据垂线段最短,则作轴于P,即为所求作的点P,
此时P点的坐标是.
故选B.
9.【答案】A
解:连接OD、OE,如图,设的半径为r,
的内切圆O,分别与AB、BC、AC相切于点D、E、F,
,,,,
易得四边形ODBE为正方形,
,
,
,
,
.
故选:A.
10.【答案】A
解:如图,连接OA、OB、OP,延长BO交PA的延长线于点F,
,PB切于A、B两点,CD切于点E,
,,,,
的周长,
,
在和中,
,
∽,
,
,
在中,
,
,
,
解得,
,
故选A.
11.【答案】.
解:根据题意可知,点O从A沿着AC移动,当O移动到如图1时,
即与CD相切,与矩形各边的交点个数为4个,
当O继续移动,会出现5的交点的情况.
图1是一种临界情况,
分别过O作CD,AD的垂线段OE,OF,
与CD相切,,
四边形ABCD是矩形,
,
又,,
,
,,
∽,
,
在中,,
,,
,
,,
,
即,,
与矩形各边的交点个数为5个时,,
点O继续移动到如图2时,即与BC相切,
与矩形各边的交点个数为6个,在此之前的交点是5个,
图2又是一种临界情况,
分别过O作BC,AB的垂线段OG,OH,
与BC相切,,
又,,
,
,,
∽,
,
,
,
即,得,
与矩形各边的交点个数为5个时,,
综上,.
故本题答案为:.
12.【答案】
解:过点P作于H,轴于D,交直线于E,连结PA,
与y轴相切于点C,
轴,
点的横坐标为3,
点坐标为,
和都是等腰直角三角形,
,
,
在中,,
,
,
点坐标为
故答案为
13.【答案】
解:是的内心
平分,BP平分,
,,
,
,
,,
,
;
为的外接圆的圆心,BD为的外接圆半径
,
是直径,
,
外接圆的半径为
14.【答案】
解:连接AB,
、PB是的切线,
,
,
,
,
,
故答案为:.
15.【答案】
解:在中,,,设,,
,
点O为的内心,
,
,
解得,
四边形CDOE是正方形,
,
,
,
故答案为.
16.【答案】
解:作与的角平分线交于点O,过O作,
则,,
故B,
设,则,,
在中,
,
解得或舍去,
四边形的内切圆半径为.
故答案为.
17.【答案】 或
解:直线交x轴于点A,交y轴于点B,
令,得,令,得,
,,
,,
,
如图,当点P在点A右侧时,
设与直线AB相切于C,连接PC,PB,
则,,
设,则,
,
即,
解得:,;
如图,当点P在点A左侧时,
设与直线AB相切于D,连接PD,PB,
则,,
设,则,
,
即,
解得:,;
综上所述,点P的坐标为 或,
故答案为 或.
18.【答案】
解:过P点作正三角形的三边的平行线,即交BC、AC于Q、M,交AB、AC于R、N,交AB、BC于S、O,
是等边三角形,
,,都是正三角形,
,,,
四边形ASPM,四边形NCOP,四边形PQBR是平行四边形,
可知黑色部分的面积白色部分的面积,
,
,
设边AB的高为h,,
,即,
,
,
,
三角形ABC的高,
的内切圆半径.
故答案为.
19.【答案】证明:是半圆O的直径,
,
,
,
即,
是半圆O的切线;
解:,
,
,,
,
,
∽,
,即,
20.【答案】解:四边形ABCD是正方形,.
、BP都是的切线 又是的切线, ,
四边形CDFP的周长为 .
21.【答案】解:是的直径,
,
又,
,
,
,
的半径为;
连结AI,
是的内心.
,
,
,
,
,
,
即.
22.【答案】解:证明:如图1,连接DE,
为圆的直径,
,
即:
轴
点D在上
直线OD为的切线.
如图2,当F位于AB上时,过作于N,
∽
,,
,即AB:BC::8::4:5
设,则,
,解得:,
经检验是原方程的解,
即
如图3,当F位于BA的延长线上时,过作于M,
∽
设,则,
解得:,
经检验是原方程的解,
即
故答案为:,.
如图4,为直径,
∽
,
令
当时,
此时
.
23.【答案】解:如图所示,依题意画出图形G为,如图所示,
平分,,
,
.
,
在和中
≌,
,
为弦DM的垂直平分线.
为的直径,连接OD,
,,
,
.
又,
,
,即,
为的切线.
直线DE与图形G的公共点个数为1个.
24.【答案】解:如图2,连接OA、OB、OC、OD.
,.
如图3,过点D作于E,
梯形ABCD为等腰梯形,
,
,
在中,,,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙教版九年级数学下册单元测试卷
第二章 直线与圆的位置关系
姓名:___________班级:___________学号:___________
一、选择题(本大题共10小题,共30.0分)
如图,正六边形ABCDEF内接于,若直线PA与相切于点A,则
A.
B.
C.
D.
已知直线l:与以原点O为圆心,5为半径的相交,则b的取值范围为
A. B.
C. D. 或
在平面直角坐标系中,以点为圆心,半径为3的圆一定
A. 与x轴相切,与y轴相切 B. 与x轴相切,与y轴相交
C. 与x轴相交,与y轴相切 D. 与x轴相交,与y轴相交
下列事件中,三点确定一个圆;平分弦的直径垂直于弦;从圆外一点可以引圆的两条切线,它们的切线长相等;关于x的一元二次方程有实数根,则a的取值范围是;圆心角是圆周角的2倍。其中必然事件的个数有
A. 1 B. 2 C. 3 D. 4
如图,AB为半圆O的直径,AD、BC分别切于A,B两点,CD切于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OC,,则四边形ABCD的周长为
A. B.
C. D.
已知,如图,四边形ABCD内接于,AB为的直径,MN切于C,,则的度数为
A. B.
C. D.
在中,,,,O是的内心,以O为圆心,r为半径的圆与线段AB有公共点,则r的取值范围是
A. B. C. D.
在平面直角坐标系中,半径为1的的圆心坐标为,若P是x轴上一动点,PQ是的切线,Q为切点,则当PQ最短时P点的坐标为
A. B.
C. D. 或
如图在中,,,作的内切圆圆O,分别与AB、BC、AC相切于点D、E、F,设,的面积为S,则S关于x的函数图像大致为
A. B.
C. D.
如图,PA,PB切于A、B两点,CD切于点E,交PA,PB于C、D,若的半径为r,的周长等于3r,则的值是
A. B.
C. D.
二、填空题(本大题共8小题,共24.0分)
在矩形ABCD中,,点O为对角线AC上一点不与A重合,是以点O为圆心,AO为半径的圆当与矩形各边的交点个数为5个时,半径OA的范围是________.
如图,在平面直角坐标系中,函数的图象被截得的弦AB的长为,与y轴相切,半径为3,圆心P位于第一象限内且在直线的上方,则点P坐标是________.
P是的内心,,,则的外接圆半径为_______.
如图,PA、PB是的切线,A、B为切点,点C、D在上.若,则________.
已知在ABC中,C,ABC,若点O为ABC的内心,则OAC______.
将正方形ABCD绕点A按逆时针方向旋转,得正方形,交CD于点E,,则四边形的内切圆半径为__________。
如图,直线交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作,当与直线AB相切时,点P的坐标是______.
如图,等边中,P为三角形内一点,过P作,,,连结AP、BP、CP,如果,那么的内切圆半径为_________.
三、解答题(本大题共6小题,共46.0分)
如图,AB是半圆O的直径,AD为弦,.
求证:BC是半圆O的切线;
若,OC交BD于E,,,求AD的长.
已知正方形ABCD的边长为2,M是BC的中点,P是线段MC上的一个动点,点P不与点M,C重合,以AB为直径作,过点P作的切线交AD于点F,切点为求四边形CDFP的周长.
如图,四边形ABCD是的内接四边形,对角线AC是的直径,,I是的内心,.
求半径的长.
求证:.
已知在平面直角坐标系中,点,,,以线段BC为直径作圆,圆心为E,直线AC交于点D,连接OD.
求证:直线OD是的切线;
点F为x轴上任意一动点,连接CF交于点G,连接BG;
当时,求所有F点的坐标______直接写出;
求的最大值.
如图所示,在平面内,给定不在同一直线上的点A,B,C,射线BP是的平分线,点O到点A,B,C的距离均等于为常数,到点O的距离等于a的所有点组成图形G,图形G交射线BP于点D,连接AD,CD.
求证:;
过点D作直线AB的垂线DE,垂足为E,作于点F,延长DF交图形G于点M,连接若,求直线DE与图形G的公共点个数.
阅读材料:
已知,如图,在面积为S的中,,,,内切圆O的半径为连接OA、OB、OC,被划分为三个小三角形.
.
.
类比推理:若面积为S的四边形ABCD存在内切圆与各边都相切的圆,如图,各边长分别为,,,,求四边形的内切圆半径r;
理解应用:如图,在等腰梯形ABCD中,,,,,与分别为与的内切圆,设它们的半径分别为和,求的值.
答案和解析
1.【答案】A
解:连接OB,AD,BD,
多边形ABCDEF是正多边形,
为外接圆的直径,
,
.
直线PA与相切于点A,
,
故选:A.
2.【答案】C
解:如图,假设直线:交x轴与A,交y轴与B,
则:,
,
假设直线:与圆相切,切点是C,
则, .
,
,
.
直线l:与相交时b的取值范围为
.
故选:C
3.【答案】B
解:点到x轴的距离是3,等于半径,
到y轴的距离是2,小于半径,
圆与y轴相交,与x轴相切.
故选B.
4.【答案】A
略
5.【答案】D
解:过D作于F,则,
、BC分别切于A、B两点,CD切于点E,
,,,
四边形ADFB是矩形,
,,
,,,,
,,
,,
在中,由勾股定理得:,
即,
即四边形ABCD的周长是,
故选D.
6.【答案】B
略
7.【答案】B
解:如图,作于D,于E,于F,连接OA、OB,
则四边形OECF是正方形,
,
,,,
,
是的内心,
,
,,
,,
当时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当时,以O为圆心,r为半径的圆与线段AB有两个交点;
当时,以O为圆心,r为半径的圆与线段AB有1个交点;
以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是;
故选B
8.【答案】B
解:连接AQ,AP,如图,
根据切线的性质定理,得,
要使PQ最小,只需AP最小,
则根据垂线段最短,则作轴于P,即为所求作的点P,
此时P点的坐标是.
故选B.
9.【答案】A
解:连接OD、OE,如图,设的半径为r,
的内切圆O,分别与AB、BC、AC相切于点D、E、F,
,,,,
易得四边形ODBE为正方形,
,
,
,
,
.
故选:A.
10.【答案】A
解:如图,连接OA、OB、OP,延长BO交PA的延长线于点F,
,PB切于A、B两点,CD切于点E,
,,,,
的周长,
,
在和中,
,
∽,
,
,
在中,
,
,
,
解得,
,
故选A.
11.【答案】.
解:根据题意可知,点O从A沿着AC移动,当O移动到如图1时,
即与CD相切,与矩形各边的交点个数为4个,
当O继续移动,会出现5的交点的情况.
图1是一种临界情况,
分别过O作CD,AD的垂线段OE,OF,
与CD相切,,
四边形ABCD是矩形,
,
又,,
,
,,
∽,
,
在中,,
,,
,
,,
,
即,,
与矩形各边的交点个数为5个时,,
点O继续移动到如图2时,即与BC相切,
与矩形各边的交点个数为6个,在此之前的交点是5个,
图2又是一种临界情况,
分别过O作BC,AB的垂线段OG,OH,
与BC相切,,
又,,
,
,,
∽,
,
,
,
即,得,
与矩形各边的交点个数为5个时,,
综上,.
故本题答案为:.
12.【答案】
解:过点P作于H,轴于D,交直线于E,连结PA,
与y轴相切于点C,
轴,
点的横坐标为3,
点坐标为,
和都是等腰直角三角形,
,
,
在中,,
,
,
点坐标为
故答案为
13.【答案】
解:是的内心
平分,BP平分,
,,
,
,
,,
,
;
为的外接圆的圆心,BD为的外接圆半径
,
是直径,
,
外接圆的半径为
14.【答案】
解:连接AB,
、PB是的切线,
,
,
,
,
,
故答案为:.
15.【答案】
解:在中,,,设,,
,
点O为的内心,
,
,
解得,
四边形CDOE是正方形,
,
,
,
故答案为.
16.【答案】
解:作与的角平分线交于点O,过O作,
则,,
故B,
设,则,,
在中,
,
解得或舍去,
四边形的内切圆半径为.
故答案为.
17.【答案】 或
解:直线交x轴于点A,交y轴于点B,
令,得,令,得,
,,
,,
,
如图,当点P在点A右侧时,
设与直线AB相切于C,连接PC,PB,
则,,
设,则,
,
即,
解得:,;
如图,当点P在点A左侧时,
设与直线AB相切于D,连接PD,PB,
则,,
设,则,
,
即,
解得:,;
综上所述,点P的坐标为 或,
故答案为 或.
18.【答案】
解:过P点作正三角形的三边的平行线,即交BC、AC于Q、M,交AB、AC于R、N,交AB、BC于S、O,
是等边三角形,
,,都是正三角形,
,,,
四边形ASPM,四边形NCOP,四边形PQBR是平行四边形,
可知黑色部分的面积白色部分的面积,
,
,
设边AB的高为h,,
,即,
,
,
,
三角形ABC的高,
的内切圆半径.
故答案为.
19.【答案】证明:是半圆O的直径,
,
,
,
即,
是半圆O的切线;
解:,
,
,,
,
,
∽,
,即,
20.【答案】解:四边形ABCD是正方形,.
、BP都是的切线 又是的切线, ,
四边形CDFP的周长为 .
21.【答案】解:是的直径,
,
又,
,
,
,
的半径为;
连结AI,
是的内心.
,
,
,
,
,
,
即.
22.【答案】解:证明:如图1,连接DE,
为圆的直径,
,
即:
轴
点D在上
直线OD为的切线.
如图2,当F位于AB上时,过作于N,
∽
,,
,即AB:BC::8::4:5
设,则,
,解得:,
经检验是原方程的解,
即
如图3,当F位于BA的延长线上时,过作于M,
∽
设,则,
解得:,
经检验是原方程的解,
即
故答案为:,.
如图4,为直径,
∽
,
令
当时,
此时
.
23.【答案】解:如图所示,依题意画出图形G为,如图所示,
平分,,
,
.
,
在和中
≌,
,
为弦DM的垂直平分线.
为的直径,连接OD,
,,
,
.
又,
,
,即,
为的切线.
直线DE与图形G的公共点个数为1个.
24.【答案】解:如图2,连接OA、OB、OC、OD.
,.
如图3,过点D作于E,
梯形ABCD为等腰梯形,
,
,
在中,,,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
