2020-2021学年浙教版八年级数学下册第五章《特殊的平行四边形》单元提高卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年浙教版八年级数学下册第五章《特殊的平行四边形》单元提高卷(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 763.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 10:49:46 | ||
图片预览



文档简介
第五章《特殊的平行四边形》单元提高卷
一、选择题(每题3分,共30分)
1.正方形是轴对称图形,它的对称轴共有( )
A.1条 B.2条 C.3条 D.4条
2.下列性质中,菱形对角线不具有的是( )
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
851535450853.下列关于 ABCD的叙述,正确的是( )
440436053340148971053340A.若AB⊥BC,则 ABCD是菱形 B.若AC⊥BD,则 ABCD是正方形
443293552070151828552070C.若AC = BD,则 ABCD是矩形 D.若AB = AD,则 ABCD是正方形
4.如图所示,点E在正方形ABCD外,∠AEB = 90°,若AE = 6,BE = 8,则正方形ABCD的面积是( )
A.48 B.24 C.10 D.100
5.菱形OABC在平面直角坐标系中的位置如图所示,∠A0C = 45°,OC = false,则点B的坐标为( )
A.(false + 1,1) B.(1,false + 1) C.(false,1) D.(1,false)
6.如图所示为一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下.对于甲、乙两人的作法,可判断( )
A.甲、乙均正确 B.甲、乙均错误 C.甲正确,乙错误 D.甲错误,乙正确
54197253251207.如图所示,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中,不一定成立的是( )
A.∠ABC = ∠ADC,∠BAD = ∠BCD B.AB = BC
C.AB = CD,AD = BC D.∠DAB + ∠BCD = 180°
8.如图所示,在菱形ABCD中,点M,N分别在AB,CD上,且AM = CN,MN与AC交于点O,连结BO.若∠DAC = 26°,则∠OBC的度数为( )
A.54° B.64° C.74° D.26°
9.如图所示,四边形ABCD是正方形,AB = 1,F是对角线AC延长线上一点,以BC,CF为邻边作菱形BEFC,连结DE,则DE的长是( )
A.false B.1 + false C.false D.2
10.如图所示,在正方形ABCD中,P是AB上一动点(点P不与点A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.有下列结论:①△APE≌△AME;②PM + PN = BD;③PE2 + PF2 = PO2.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每题4分,共24分)
11.如图所示,在矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点.若MN = 4,则AC的长为 _________ .
12.如图所示,延长正方形ABCD边BC至点E,使CE = AC,则∠AFC = _________ .
13.如图所示,矩形ABCD的对角线AC,BD相交于点O,∠AOB = 120°,CE∥BD,DE∥AC,若AD = 4,则四边形CODE的周长是 _________ .
14.如图所示,在边长为4的正方形ABCD中,M为对角线BD上一动点,ME⊥BC于点E,MF⊥CD于点F,则EF的最小值为 _________ .
15.已知矩形ABCD的对角线相交于点O,AE平分∠BAD交矩形的边于点E,若∠CAE = 10°,则∠AOB的度数为 _________ .
16.如图所示,在菱形ABCD中,AB = false,∠B = 120°,E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD边上,DG = DE.若△EFG是等腰三角形,则DE的长为 _________ .
三、解答题(共66分)
17.(6分)已知菱形ABCD的周长是200,其中一条对角线长60.求:
(1)另一条对角线的长度.
(2)菱形ABCD的面积.
18.(8分)如图所示,四边形ABCD是矩形,E为CD边上一点,且AE,BE分别平分∠DAB,∠ABC.
(1)求证:△ADE≌△BCE.
(2)已知AD = 2,求AB的长度.
19.(8分)如图所示,在四边形ABCD中,点E是线段AD上的任意一点(点E与点A,D不重合),G,F,H分别是BE,BC,CE的中点.
(1)求证:四边形EGFH是平行四边形.
(2)EF和BC满足什么关系时,四边形EGFH是正方形?
20.(10分)如图所示,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的点F处,DF交BC于点E.
(1)求证:△DCE≌△BFE.
(2)若CD = 2,∠ADB = 30°,求BE的长.
21.(10分)在Rt△ABC中,∠BAC = 90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB.
(2)求证:四边形ADCF是菱形.
(3)若AC = 4,AB = 5,求菱形ADCF的面积.
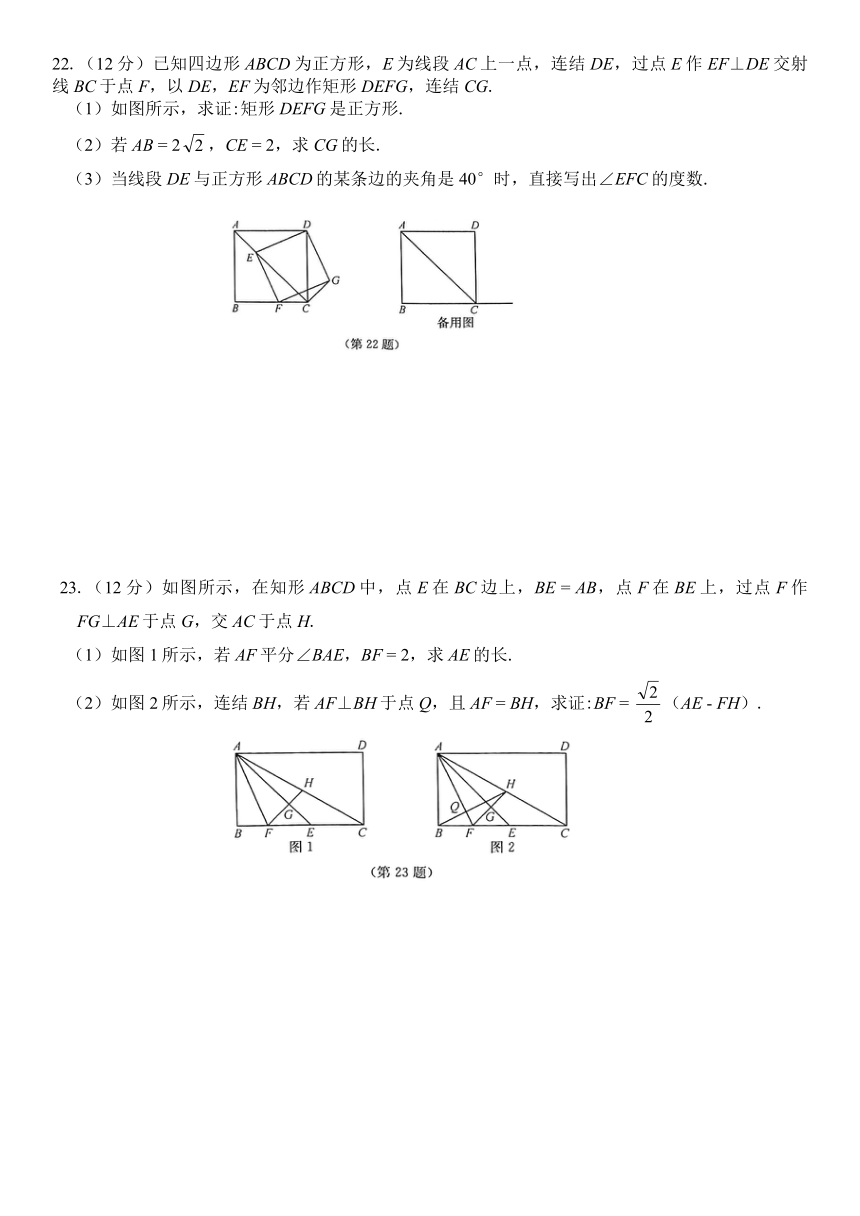
22.(12分)已知四边形ABCD为正方形,E为线段AC上一点,连结DE,过点E作EF⊥DE交射线BC于点F,以DE,EF为邻边作矩形DEFG,连结CG.
(1)如图所示,求证:矩形DEFG是正方形.
(2)若AB = 2false,CE = 2,求CG的长.
(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.
23.(12分)如图所示,在知形ABCD中,点E在BC边上,BE = AB,点F在BE上,过点F作FG⊥AE于点G,交AC于点H.
(1)如图1所示,若AF平分∠BAE,BF = 2,求AE的长.
(2)如图2所示,连结BH,若AF⊥BH于点Q,且AF = BH,求证:BF = false(AE - FH).
一、选择题(每题3分,共30分)
1.正方形是轴对称图形,它的对称轴共有( )
A.1条 B.2条 C.3条 D.4条
2.下列性质中,菱形对角线不具有的是( )
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
851535450853.下列关于 ABCD的叙述,正确的是( )
440436053340148971053340A.若AB⊥BC,则 ABCD是菱形 B.若AC⊥BD,则 ABCD是正方形
443293552070151828552070C.若AC = BD,则 ABCD是矩形 D.若AB = AD,则 ABCD是正方形
4.如图所示,点E在正方形ABCD外,∠AEB = 90°,若AE = 6,BE = 8,则正方形ABCD的面积是( )
A.48 B.24 C.10 D.100
5.菱形OABC在平面直角坐标系中的位置如图所示,∠A0C = 45°,OC = false,则点B的坐标为( )
A.(false + 1,1) B.(1,false + 1) C.(false,1) D.(1,false)
6.如图所示为一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下.对于甲、乙两人的作法,可判断( )
A.甲、乙均正确 B.甲、乙均错误 C.甲正确,乙错误 D.甲错误,乙正确
54197253251207.如图所示,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中,不一定成立的是( )
A.∠ABC = ∠ADC,∠BAD = ∠BCD B.AB = BC
C.AB = CD,AD = BC D.∠DAB + ∠BCD = 180°
8.如图所示,在菱形ABCD中,点M,N分别在AB,CD上,且AM = CN,MN与AC交于点O,连结BO.若∠DAC = 26°,则∠OBC的度数为( )
A.54° B.64° C.74° D.26°
9.如图所示,四边形ABCD是正方形,AB = 1,F是对角线AC延长线上一点,以BC,CF为邻边作菱形BEFC,连结DE,则DE的长是( )
A.false B.1 + false C.false D.2
10.如图所示,在正方形ABCD中,P是AB上一动点(点P不与点A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.有下列结论:①△APE≌△AME;②PM + PN = BD;③PE2 + PF2 = PO2.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(每题4分,共24分)
11.如图所示,在矩形ABCD中,AC,BD交于点O,M,N分别为BC,OC的中点.若MN = 4,则AC的长为 _________ .
12.如图所示,延长正方形ABCD边BC至点E,使CE = AC,则∠AFC = _________ .
13.如图所示,矩形ABCD的对角线AC,BD相交于点O,∠AOB = 120°,CE∥BD,DE∥AC,若AD = 4,则四边形CODE的周长是 _________ .
14.如图所示,在边长为4的正方形ABCD中,M为对角线BD上一动点,ME⊥BC于点E,MF⊥CD于点F,则EF的最小值为 _________ .
15.已知矩形ABCD的对角线相交于点O,AE平分∠BAD交矩形的边于点E,若∠CAE = 10°,则∠AOB的度数为 _________ .
16.如图所示,在菱形ABCD中,AB = false,∠B = 120°,E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD边上,DG = DE.若△EFG是等腰三角形,则DE的长为 _________ .
三、解答题(共66分)
17.(6分)已知菱形ABCD的周长是200,其中一条对角线长60.求:
(1)另一条对角线的长度.
(2)菱形ABCD的面积.
18.(8分)如图所示,四边形ABCD是矩形,E为CD边上一点,且AE,BE分别平分∠DAB,∠ABC.
(1)求证:△ADE≌△BCE.
(2)已知AD = 2,求AB的长度.
19.(8分)如图所示,在四边形ABCD中,点E是线段AD上的任意一点(点E与点A,D不重合),G,F,H分别是BE,BC,CE的中点.
(1)求证:四边形EGFH是平行四边形.
(2)EF和BC满足什么关系时,四边形EGFH是正方形?
20.(10分)如图所示,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的点F处,DF交BC于点E.
(1)求证:△DCE≌△BFE.
(2)若CD = 2,∠ADB = 30°,求BE的长.
21.(10分)在Rt△ABC中,∠BAC = 90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB.
(2)求证:四边形ADCF是菱形.
(3)若AC = 4,AB = 5,求菱形ADCF的面积.
22.(12分)已知四边形ABCD为正方形,E为线段AC上一点,连结DE,过点E作EF⊥DE交射线BC于点F,以DE,EF为邻边作矩形DEFG,连结CG.
(1)如图所示,求证:矩形DEFG是正方形.
(2)若AB = 2false,CE = 2,求CG的长.
(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.
23.(12分)如图所示,在知形ABCD中,点E在BC边上,BE = AB,点F在BE上,过点F作FG⊥AE于点G,交AC于点H.
(1)如图1所示,若AF平分∠BAE,BF = 2,求AE的长.
(2)如图2所示,连结BH,若AF⊥BH于点Q,且AF = BH,求证:BF = false(AE - FH).
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
