2020-2021学年浙教新版九年级下册数学《第2章 直线与圆的位置关系》单元测试卷(word有答案)
文档属性
| 名称 | 2020-2021学年浙教新版九年级下册数学《第2章 直线与圆的位置关系》单元测试卷(word有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 455.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 22:16:45 | ||
图片预览

文档简介
2020-2021学年浙教新版九年级下册数学《第2章
直线与圆的位置关系》单元测试卷
一.选择题
1.在平面直角坐标系中,以点P(1,2)为圆心,以P为圆心,以1为半径的圆必与x轴有多少个公共点( )
A.0
B.1
C.2
D.3
2.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆
B.以OB为半径的圆
C.以OC为半径的圆
D.以OD为半径的圆
3.如图,四边形ABCD内接于⊙O,AB=BC.AT是⊙O的切线,∠BAT=55°,则∠D等于( )
A.110°
B.115°
C.120°
D.125°
4.如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=( )
A.6
B.7
C.8
D.9
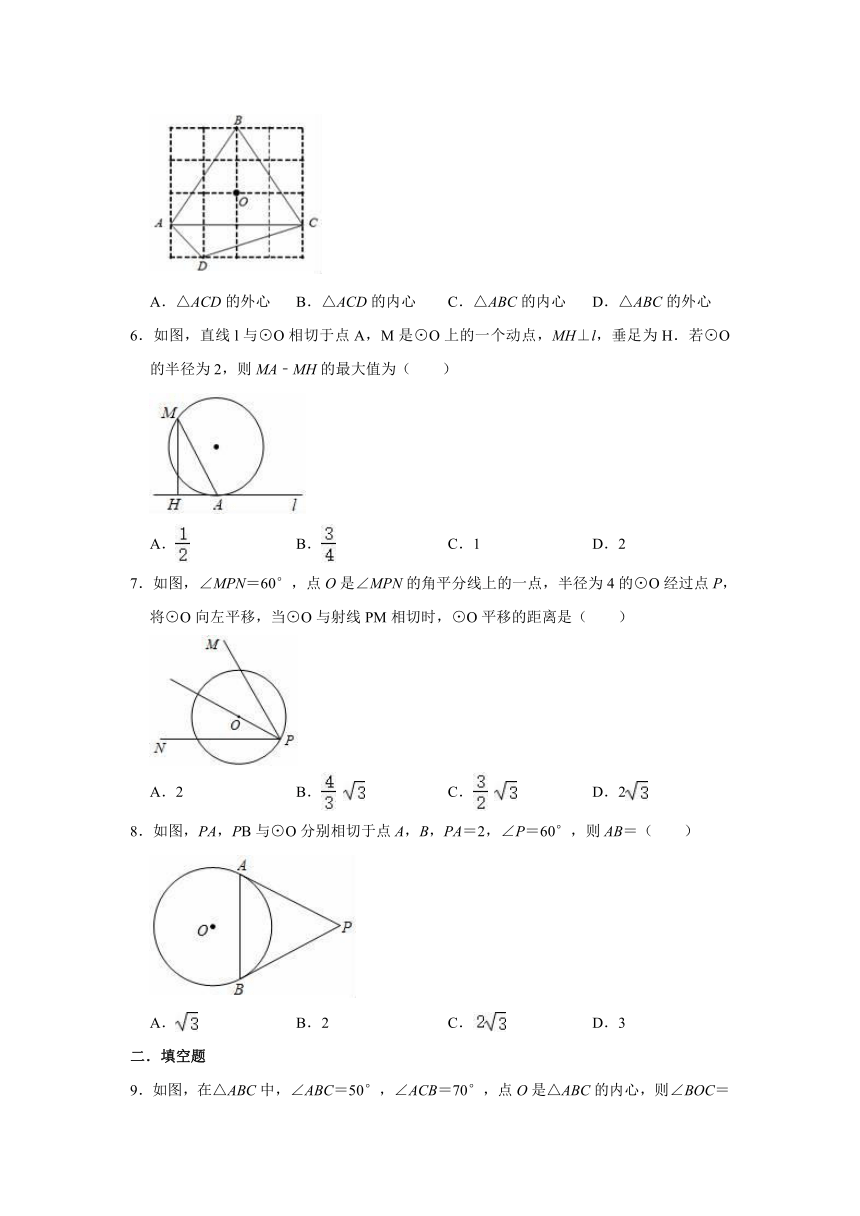
5.如图所示,在4×4的网格中,A,B,C,D,O均在格点上,则点O是( )
A.△ACD的外心
B.△ACD的内心
C.△ABC的内心
D.△ABC的外心
6.如图,直线l与⊙O相切于点A,M是⊙O上的一个动点,MH⊥l,垂足为H.若⊙O的半径为2,则MA﹣MH的最大值为( )
A.
B.
C.1
D.2
7.如图,∠MPN=60°,点O是∠MPN的角平分线上的一点,半径为4的⊙O经过点P,将⊙O向左平移,当⊙O与射线PM相切时,⊙O平移的距离是( )
A.2
B.
C.
D.2
8.如图,PA,PB与⊙O分别相切于点A,B,PA=2,∠P=60°,则AB=( )
A.
B.2
C.
D.3
二.填空题
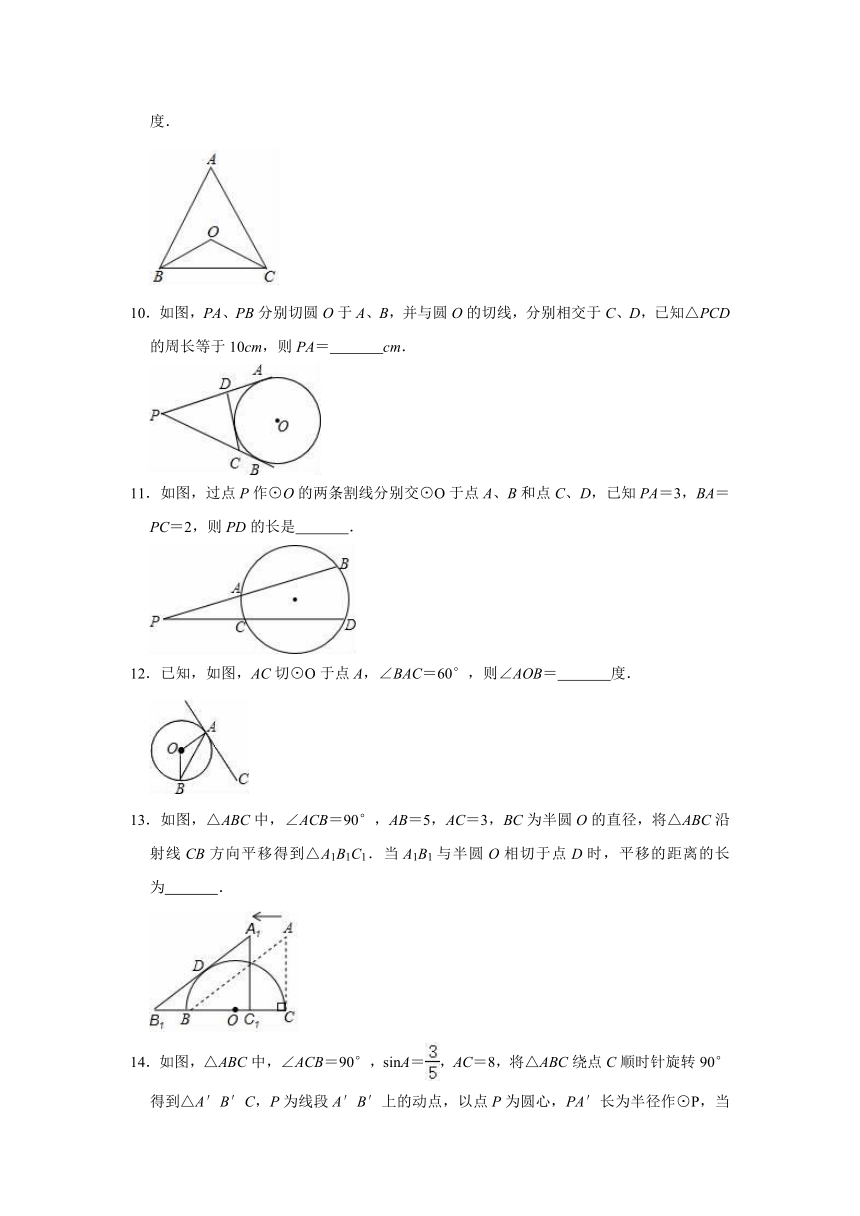
9.如图,在△ABC中,∠ABC=50°,∠ACB=70°,点O是△ABC的内心,则∠BOC=
度.
10.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA=
cm.
11.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,BA=PC=2,则PD的长是
.
12.已知,如图,AC切⊙O于点A,∠BAC=60°,则∠AOB=
度.
13.如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为
.
14.如图,△ABC中,∠ACB=90°,sinA=,AC=8,将△ABC绕点C顺时针旋转90°得到△A′B′C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为
.
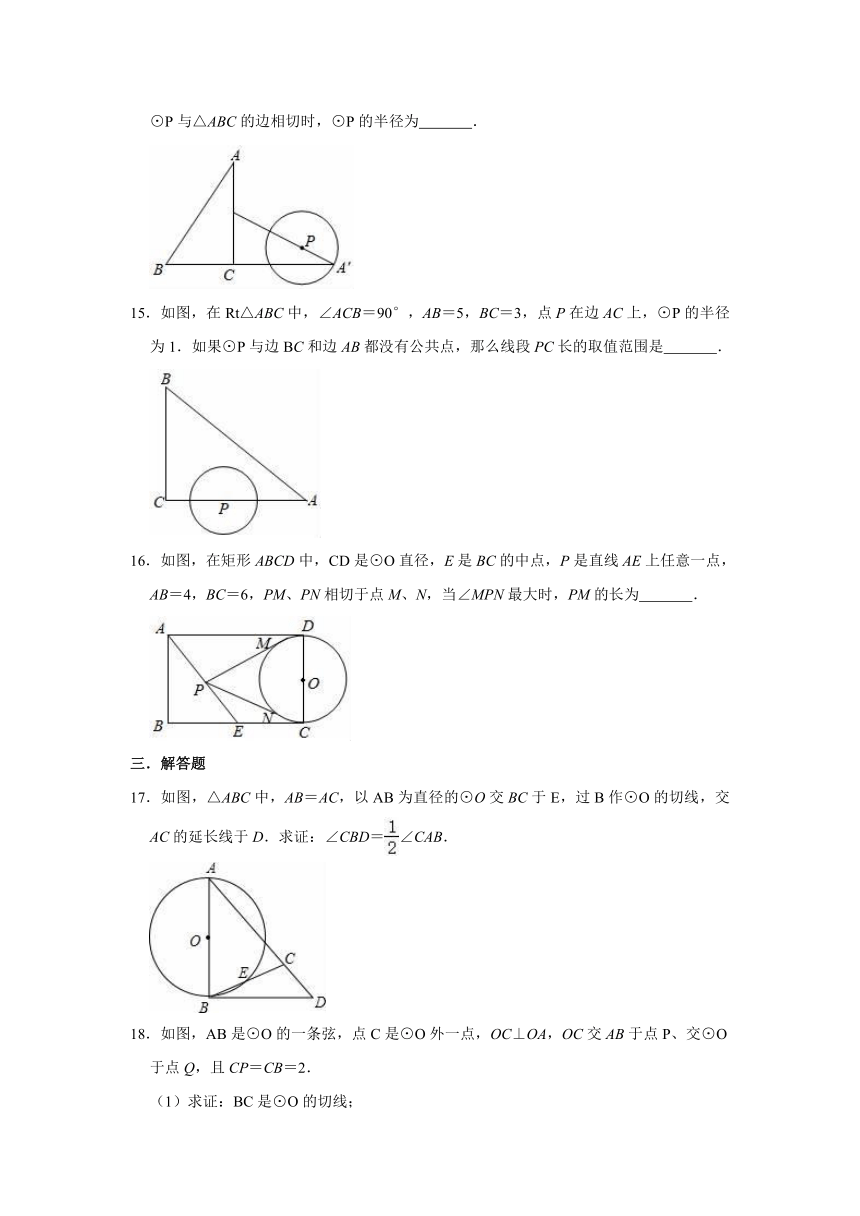
15.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是
.
16.如图,在矩形ABCD中,CD是⊙O直径,E是BC的中点,P是直线AE上任意一点,AB=4,BC=6,PM、PN相切于点M、N,当∠MPN最大时,PM的长为
.
三.解答题
17.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD=∠CAB.
18.如图,AB是⊙O的一条弦,点C是⊙O外一点,OC⊥OA,OC交AB于点P、交⊙O于点Q,且CP=CB=2.
(1)求证:BC是⊙O的切线;
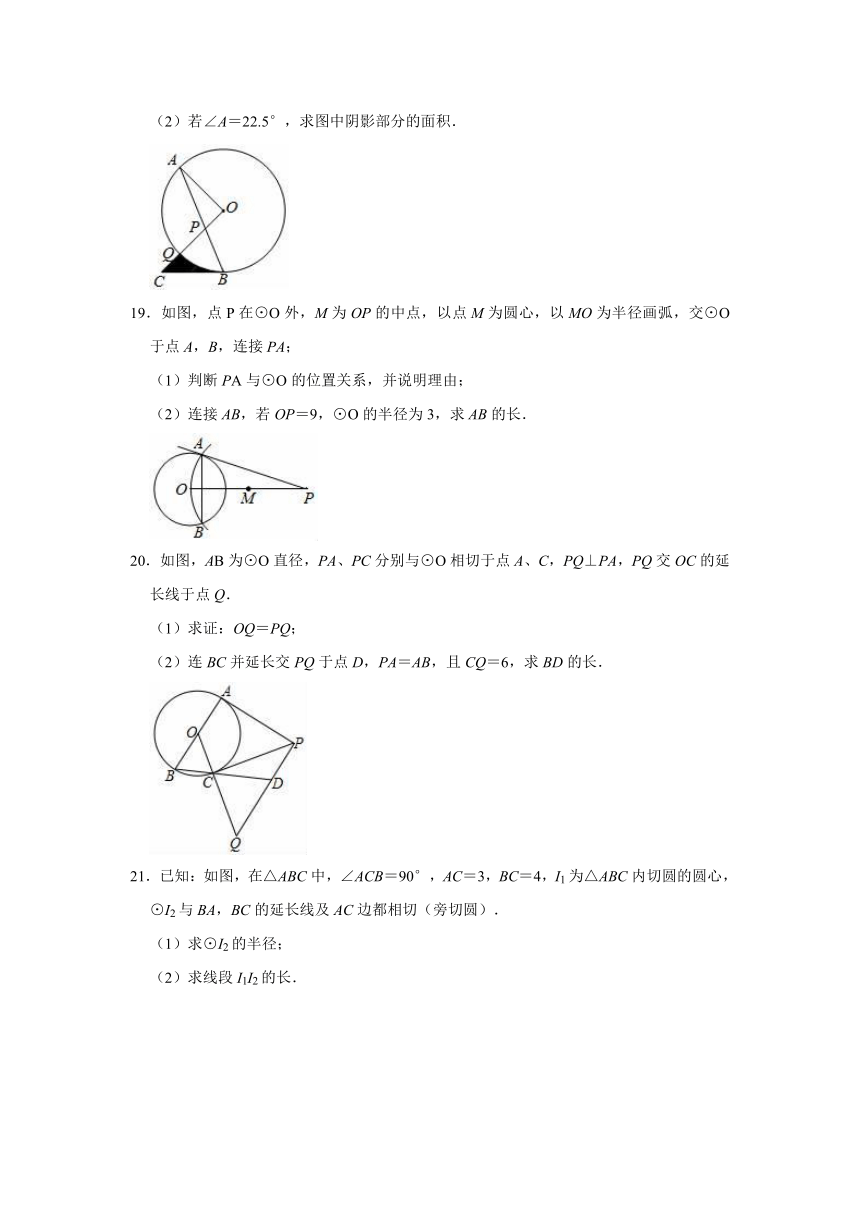
(2)若∠A=22.5°,求图中阴影部分的面积.
19.如图,点P在⊙O外,M为OP的中点,以点M为圆心,以MO为半径画弧,交⊙O于点A,B,连接PA;
(1)判断PA与⊙O的位置关系,并说明理由;
(2)连接AB,若OP=9,⊙O的半径为3,求AB的长.
20.如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
21.已知:如图,在△ABC中,∠ACB=90°,AC=3,BC=4,I1为△ABC内切圆的圆心,⊙I2与BA,BC的延长线及AC边都相切(旁切圆).
(1)求⊙I2的半径;
(2)求线段I1I2的长.
22.如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=20,BC=16,求CD的长.
23.如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,∠DBC=∠BAC,⊙O经过A、B、D三点,连接DO并延长交⊙O于点E,连接AE,DE与AB交于点F.
(1)求证:CB是⊙O的切线;
(2)求证:AB=EB;
(3)若DF=3,EF=7,求BC的长.
参考答案与试题解析
一.选择题
1.解:∵P(1,2),即2>1,
∴以P为圆心,以1为半径的圆与x轴的位置关系是相离,
∴该圆与x轴的交点有0个.
故选:A.
2.解:∵OD⊥a于D,
∴以点O为圆心,OD为半径的圆与直线a相切.
故选:D.
3.解:如图,连接AC,
由弦切角定理知∠ACB=∠BAT=55°,
∵AB=BC,
∴∠ACB=∠CAB=55°,
∴∠B=180°﹣2∠ACB=70°,
∴∠D=180°﹣∠B=110°.
故选:A.
4.解:∵PB,PD是⊙O的割线,
∴PA?PB=PC?PD,
∵PA=2,PC=CD=3,
∴2PB=3×6
解得:PB=9.
故选:D.
5.解:由勾股定理可知:
OA=OD=OC==,
所以点O是△ACD的外心,
故选:A.
6.解:如图,连接AO并延长交圆O于点C,连接CM,
设BH=b,MA=a,
∵直线l与⊙O相切于点A,
∴连接OA交圆O于点C,
则∠CAH=90°,
又∵∠MHA=90°,
∴AC∥HM,
∴∠HMA=∠MAC,
∵AC为直径,
∴∠CMA=90°.
∴△AMH∽△CAM,
∴=,CA=4,
∴=,
∴a2=4b,b=,
∴a﹣b=a﹣=﹣(a﹣2)2+1,
∴当a=2时,a﹣b的最大值为1.
则MA﹣MH的最大值为1.
故选:C.
7.解:设⊙O'为⊙O向左平移后与PM相切的圆,切点为B,连接O'B交PO于D,过O作OA⊥PM于A,OC⊥O'B于C,如图所示:
则OO'即为⊙O平移的距离,O'B=OP=4,O'B⊥PM,
∵∠MPN=60°,PO是∠MPN的平分线,
∴∠MPO=∠OPN=∠MPN=30°,
∵OA⊥OM,
∴OA=OP=2,
∵OA⊥PM,OC⊥O'B,O'B⊥PM,
∴四边形OABC是矩形,
∴BC=OA=2,
∴O'C=O'B﹣BC=2,
由平移的性质得:OO'∥PN,
∴∠DOO'=∠OPN=30°,
∵O'B⊥PM,
∴∠O'BP=90°,
∴∠BDP=90°﹣∠MPO=60°,
∵∠BDP=∠DOO'+∠DO'O,
∴∠DO'O=∠BDP﹣∠DOO'=30°,
∴OC=O'C=,OO'=2OC=,
即⊙O平移的距离为,
故选:B.
8.解:∵PA,PB与⊙O分别相切于点A,B,
∴PA=PB,∵∠APB=60°,
∴△PAB是等边三角形,
∴AB=AP=2.
故选:B.
二.填空题
9.解:∵点O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC=×50°=25°,∠OCB=∠ACB=×70°=35°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣25°﹣35°=120°.
故答案为120.
10.解:如图,设DC与⊙O的切点为E;
∵PA、PB分别是⊙O的切线,且切点为A、B;
∴PA=PB;
同理,可得:DE=DA,CE=CB;
则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);
∴PA=PB=5cm,
故答案为:5.
11.解:∵PAB,PCD是圆的两条割线,∴PA?PB=PC?PD,
∵PA=3,BA=PC=2,∴3×5=2PD,
∴PD=7.5.
故答案为7.5.
12.解:∵AC切⊙O于点A,
∴∠AOB=2∠BAC=120°.
13.解:连接OG,如图,
∵∠BAC=90°,AB=5,AC=3,
∴BC==4,
∵Rt△ABC沿射线CB方向平移,当A1B1与半圆O相切于点D,得△A1B1C1,
∴CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,
∵A1B1与半圆O相切于点D,
∴OD⊥A1B1,
∵BC=4,线段BC为半圆O的直径,
∴OB=OC=2,
∵∠B1=∠B1,
∴Rt△B1OD∽Rt△B1A1C1,
∴=,即=,解得OB1=,
∴BB1=OB1﹣OB=﹣2=;
故答案为:.
14.解:∵,
∴设BC=3x,则AB=5x,
在Rt△ABC中,由勾股定理得,AB2=AC2+BC2,
即:(5x)2=(3x)2+82,
∴x=2,
∴AB=10,BC=6,
∴,
①若⊙P与AC相切,如图1,
设切点为M,连接PM,
则PM⊥AC,且PM⊥PA′,
∵PM⊥AC,A′C⊥AC,
∴∠B′PM=∠A′,
由旋转性质可知∠A′=∠A,
∴∠B′PM=∠A,
∴,
设PM=4x,则PA′=PM=4x,B′P=5x,
又∵A′B′=AB,
即:4x+5x=10,
解得,
∴;
②若⊙P与AB相切,延长PB′交AB于点N,如图2,
∵∠A′+∠B=∠A+∠B=90°,
∵∠A′NB=90°,
即N为AB与⊙O切点,
又∴A′B=BC+AC′=BC+AC=14,
∴A′N=A′B?cos∠A′=A′B?cosA,
即,
∴.
综上,⊙P的半径为或,
故答案为:或.
15.解:在Rt△ABC中,∠ACB=90°,AB=5,BC=3,
∴AC=4,
当⊙P与AB相切时,设切点为D,如图,
连接PD,
则PD⊥AB,
∴∠C=∠ADP=90°,
∵∠A=∠A,
∴△ADP∽△ACB,
∴,
∴=,
∴PA=,
∴PC=AC﹣PA=,
∴线段PC长的取值范围是1<CP<,
故答案为:1<CP<.
16.解:如图1,∵四边形ABCD是矩形,
∴CD=AB=4,
连接OP,OM,
∵PM,PN是⊙O的切线,
∴∠OPM=∠MPN,
要∠MPN最大,则∠OPM最大,
∵PM是⊙O的切线,
∴∠OMP=90°,
在Rt△PMO中,OM=OD=CD=2,
∴sin∠OPM==,
∴要∠OPM最大,则OP最短,
即OP⊥AE,
如图2,延长DC交直线AE于G,
∵四边形ABCD是矩形,
∴∠B=90°=∠ECG,AB∥CD,
∴∠BAE=∠G,
∵点E是BC的中点,
∴BE=BC=3,
∴△ABE≌△GCE(AAS),
∴CG=AB=4,
∵CD是⊙O的直径,
∴OC=CD=2,
∴OG=OC+CE=6,
在Rt△ABE中,AB=4,BE=3,
∴AE=5,
∵∠OPG=90°=∠B,∠G=∠BAE,
∴△ABE∽△GPO,
∴,
∴,
∴OP=,
在Rt△PMO中,PM===,
故答案为:.
三.解答题
17.证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠CAB,
∵BD是⊙O的切线,
∴∠CBD=∠BAE,
∴∠CBD=∠CAB.
18.(1)证明:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵CP=CB,
∴∠CPB=∠CBP,
∵∠CPB=∠APO,
∴∠CBP=∠APO,
在Rt△AOP中,∵∠A+∠APO=90°,
∴∠OBA+∠CBP=90°,
即:∠OBC=90°,
∴OB⊥CB,
又∵OB是半径,
∴CB与⊙O相切;
(2)解:∵∠A=22.5°,∠AOP=90°,
∴∠APO=67.5°,
∴∠BPC=∠APO=67.5°,
∵PC=CB,
∴∠CBP=67.5°,
∴∠PCB=180°﹣2∠CBP=45°,
∴∠OCB=∠POB=45°,
∴OB=BC=2,
∴图中阴影部分的面积=S△OBC﹣S扇形OBD=×2×2﹣=2﹣.
19.解:(1)PA是⊙O的切线,理由如下:
如图,连接OA,
∴OP是⊙M的直径,点A是⊙M上一点,
∴∠OAP=90°,
即OA⊥PA,
∴PA是⊙O的切线;
(2)设⊙O与OP的交点为N,AB与OP的交点为E,
连接AN,AM,BM,
∵MA=MB,OA=OB,
∴OP是线段AB的垂直平分线,
∴AB⊥OP,AE=BE,
∵OP=9,OA=3,
∴AP==6,
∴S△OAP=OA?AP=AE?OP,
∴OA?AP=AE?OP,
∴3×6=9AE,
∴AE=2,
∴AB=4.
20.(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP==4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
21.解:(1)如图,过点I2作I2Q⊥AC于点Q,连接I2S,
过点I1作I1M⊥BC于点M,I1
N⊥AC于点N,交I2S于点H,
可得四边形QCSl2,I1MCN均为正方形,I1HSM为矩形,
设⊙I2的半径为R,
则AQ=AP=3﹣R,CS=CQ=R,
又因为BP=BS,
所以5+3﹣R=4+R,
解得R=2.
(2)∵∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵I1为△ABC内切圆的圆心,
∴I1M=I1N=,
∴I1
H=3,
∴I1l2==.
22.(1)证明:连接OC,
∵DC切⊙O于C,
∴OC⊥CD,
∵AE⊥CD,
∴AE∥OC,
∵AO=BO,
∴EC=BC,
∴OC=AE,
∵OC=OA=OB=AB,
∴AE=AB;
(2)解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACE=90°,AC⊥BE,
∵由(1)知:AB=AE,
∴EC=BC,
∵BC=16,
∴EC=16,
在RtACB中,由勾股定理得:AC===15,
在Rt△ACE中,S△ACE==,
∵AE=BC=20,
∴=CD,
解得:CD=12,
23.(1)证明:在⊙O中,OB=OD,∠BAC=∠BED,
∴∠ODB=∠OBD,
∵∠DBC=∠BAC,
∴∠DBC=∠BED,
∵DE是⊙O的直径,
∴∠DBE=90°,
∴∠ODB+∠BED=90°,
∴∠OBD+∠DBC=90°,
∴OB⊥BC,
∵OB是⊙O的半径,
∴CB是⊙O的切线;
(2)证明:在⊙O中,∠ABD=∠AED,
由(1)得:∠DBC=∠BED,
∴∠ABD+∠DBC=∠AED+∠BED,
∴∠ABC=∠BEA,
∵DE是⊙O的直径,
∴∠EAC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACB=180°,
∴AE∥BC,
∴∠ABC=∠BAE,
∴∠BEA=∠BAE,
∴AB=EB;
(3)解:延长BO交AE于H,
由∠HAC=∠ACB=∠OBC=90°,得四边形ACBH是矩形,
∴OH⊥AE,
∴BC=AH=AE,
∵DF=3,EF=7,
∴直径DE=10,
即半径DO=EO=5,
∴OF=2,
∵OB∥AC,
∴=,
∴AD=,
在Rt△ADE中,AE==,
∴BC=AH=AE=.
直线与圆的位置关系》单元测试卷
一.选择题
1.在平面直角坐标系中,以点P(1,2)为圆心,以P为圆心,以1为半径的圆必与x轴有多少个公共点( )
A.0
B.1
C.2
D.3
2.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆
B.以OB为半径的圆
C.以OC为半径的圆
D.以OD为半径的圆
3.如图,四边形ABCD内接于⊙O,AB=BC.AT是⊙O的切线,∠BAT=55°,则∠D等于( )
A.110°
B.115°
C.120°
D.125°
4.如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=( )
A.6
B.7
C.8
D.9
5.如图所示,在4×4的网格中,A,B,C,D,O均在格点上,则点O是( )
A.△ACD的外心
B.△ACD的内心
C.△ABC的内心
D.△ABC的外心
6.如图,直线l与⊙O相切于点A,M是⊙O上的一个动点,MH⊥l,垂足为H.若⊙O的半径为2,则MA﹣MH的最大值为( )
A.
B.
C.1
D.2
7.如图,∠MPN=60°,点O是∠MPN的角平分线上的一点,半径为4的⊙O经过点P,将⊙O向左平移,当⊙O与射线PM相切时,⊙O平移的距离是( )
A.2
B.
C.
D.2
8.如图,PA,PB与⊙O分别相切于点A,B,PA=2,∠P=60°,则AB=( )
A.
B.2
C.
D.3
二.填空题
9.如图,在△ABC中,∠ABC=50°,∠ACB=70°,点O是△ABC的内心,则∠BOC=
度.
10.如图,PA、PB分别切圆O于A、B,并与圆O的切线,分别相交于C、D,已知△PCD的周长等于10cm,则PA=
cm.
11.如图,过点P作⊙O的两条割线分别交⊙O于点A、B和点C、D,已知PA=3,BA=PC=2,则PD的长是
.
12.已知,如图,AC切⊙O于点A,∠BAC=60°,则∠AOB=
度.
13.如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为
.
14.如图,△ABC中,∠ACB=90°,sinA=,AC=8,将△ABC绕点C顺时针旋转90°得到△A′B′C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为
.
15.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点P在边AC上,⊙P的半径为1.如果⊙P与边BC和边AB都没有公共点,那么线段PC长的取值范围是
.
16.如图,在矩形ABCD中,CD是⊙O直径,E是BC的中点,P是直线AE上任意一点,AB=4,BC=6,PM、PN相切于点M、N,当∠MPN最大时,PM的长为
.
三.解答题
17.如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于E,过B作⊙O的切线,交AC的延长线于D.求证:∠CBD=∠CAB.
18.如图,AB是⊙O的一条弦,点C是⊙O外一点,OC⊥OA,OC交AB于点P、交⊙O于点Q,且CP=CB=2.
(1)求证:BC是⊙O的切线;
(2)若∠A=22.5°,求图中阴影部分的面积.
19.如图,点P在⊙O外,M为OP的中点,以点M为圆心,以MO为半径画弧,交⊙O于点A,B,连接PA;
(1)判断PA与⊙O的位置关系,并说明理由;
(2)连接AB,若OP=9,⊙O的半径为3,求AB的长.
20.如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
21.已知:如图,在△ABC中,∠ACB=90°,AC=3,BC=4,I1为△ABC内切圆的圆心,⊙I2与BA,BC的延长线及AC边都相切(旁切圆).
(1)求⊙I2的半径;
(2)求线段I1I2的长.
22.如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.
(1)求证:AE=AB;
(2)若AB=20,BC=16,求CD的长.
23.如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,∠DBC=∠BAC,⊙O经过A、B、D三点,连接DO并延长交⊙O于点E,连接AE,DE与AB交于点F.
(1)求证:CB是⊙O的切线;
(2)求证:AB=EB;
(3)若DF=3,EF=7,求BC的长.
参考答案与试题解析
一.选择题
1.解:∵P(1,2),即2>1,
∴以P为圆心,以1为半径的圆与x轴的位置关系是相离,
∴该圆与x轴的交点有0个.
故选:A.
2.解:∵OD⊥a于D,
∴以点O为圆心,OD为半径的圆与直线a相切.
故选:D.
3.解:如图,连接AC,
由弦切角定理知∠ACB=∠BAT=55°,
∵AB=BC,
∴∠ACB=∠CAB=55°,
∴∠B=180°﹣2∠ACB=70°,
∴∠D=180°﹣∠B=110°.
故选:A.
4.解:∵PB,PD是⊙O的割线,
∴PA?PB=PC?PD,
∵PA=2,PC=CD=3,
∴2PB=3×6
解得:PB=9.
故选:D.
5.解:由勾股定理可知:
OA=OD=OC==,
所以点O是△ACD的外心,
故选:A.
6.解:如图,连接AO并延长交圆O于点C,连接CM,
设BH=b,MA=a,
∵直线l与⊙O相切于点A,
∴连接OA交圆O于点C,
则∠CAH=90°,
又∵∠MHA=90°,
∴AC∥HM,
∴∠HMA=∠MAC,
∵AC为直径,
∴∠CMA=90°.
∴△AMH∽△CAM,
∴=,CA=4,
∴=,
∴a2=4b,b=,
∴a﹣b=a﹣=﹣(a﹣2)2+1,
∴当a=2时,a﹣b的最大值为1.
则MA﹣MH的最大值为1.
故选:C.
7.解:设⊙O'为⊙O向左平移后与PM相切的圆,切点为B,连接O'B交PO于D,过O作OA⊥PM于A,OC⊥O'B于C,如图所示:
则OO'即为⊙O平移的距离,O'B=OP=4,O'B⊥PM,
∵∠MPN=60°,PO是∠MPN的平分线,
∴∠MPO=∠OPN=∠MPN=30°,
∵OA⊥OM,
∴OA=OP=2,
∵OA⊥PM,OC⊥O'B,O'B⊥PM,
∴四边形OABC是矩形,
∴BC=OA=2,
∴O'C=O'B﹣BC=2,
由平移的性质得:OO'∥PN,
∴∠DOO'=∠OPN=30°,
∵O'B⊥PM,
∴∠O'BP=90°,
∴∠BDP=90°﹣∠MPO=60°,
∵∠BDP=∠DOO'+∠DO'O,
∴∠DO'O=∠BDP﹣∠DOO'=30°,
∴OC=O'C=,OO'=2OC=,
即⊙O平移的距离为,
故选:B.
8.解:∵PA,PB与⊙O分别相切于点A,B,
∴PA=PB,∵∠APB=60°,
∴△PAB是等边三角形,
∴AB=AP=2.
故选:B.
二.填空题
9.解:∵点O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=∠ABC=×50°=25°,∠OCB=∠ACB=×70°=35°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣25°﹣35°=120°.
故答案为120.
10.解:如图,设DC与⊙O的切点为E;
∵PA、PB分别是⊙O的切线,且切点为A、B;
∴PA=PB;
同理,可得:DE=DA,CE=CB;
则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10(cm);
∴PA=PB=5cm,
故答案为:5.
11.解:∵PAB,PCD是圆的两条割线,∴PA?PB=PC?PD,
∵PA=3,BA=PC=2,∴3×5=2PD,
∴PD=7.5.
故答案为7.5.
12.解:∵AC切⊙O于点A,
∴∠AOB=2∠BAC=120°.
13.解:连接OG,如图,
∵∠BAC=90°,AB=5,AC=3,
∴BC==4,
∵Rt△ABC沿射线CB方向平移,当A1B1与半圆O相切于点D,得△A1B1C1,
∴CC1=BB1,A1C1=AC=3,A1B1=AB=5,∠A1C1B1=∠ACB=90°,
∵A1B1与半圆O相切于点D,
∴OD⊥A1B1,
∵BC=4,线段BC为半圆O的直径,
∴OB=OC=2,
∵∠B1=∠B1,
∴Rt△B1OD∽Rt△B1A1C1,
∴=,即=,解得OB1=,
∴BB1=OB1﹣OB=﹣2=;
故答案为:.
14.解:∵,
∴设BC=3x,则AB=5x,
在Rt△ABC中,由勾股定理得,AB2=AC2+BC2,
即:(5x)2=(3x)2+82,
∴x=2,
∴AB=10,BC=6,
∴,
①若⊙P与AC相切,如图1,
设切点为M,连接PM,
则PM⊥AC,且PM⊥PA′,
∵PM⊥AC,A′C⊥AC,
∴∠B′PM=∠A′,
由旋转性质可知∠A′=∠A,
∴∠B′PM=∠A,
∴,
设PM=4x,则PA′=PM=4x,B′P=5x,
又∵A′B′=AB,
即:4x+5x=10,
解得,
∴;
②若⊙P与AB相切,延长PB′交AB于点N,如图2,
∵∠A′+∠B=∠A+∠B=90°,
∵∠A′NB=90°,
即N为AB与⊙O切点,
又∴A′B=BC+AC′=BC+AC=14,
∴A′N=A′B?cos∠A′=A′B?cosA,
即,
∴.
综上,⊙P的半径为或,
故答案为:或.
15.解:在Rt△ABC中,∠ACB=90°,AB=5,BC=3,
∴AC=4,
当⊙P与AB相切时,设切点为D,如图,
连接PD,
则PD⊥AB,
∴∠C=∠ADP=90°,
∵∠A=∠A,
∴△ADP∽△ACB,
∴,
∴=,
∴PA=,
∴PC=AC﹣PA=,
∴线段PC长的取值范围是1<CP<,
故答案为:1<CP<.
16.解:如图1,∵四边形ABCD是矩形,
∴CD=AB=4,
连接OP,OM,
∵PM,PN是⊙O的切线,
∴∠OPM=∠MPN,
要∠MPN最大,则∠OPM最大,
∵PM是⊙O的切线,
∴∠OMP=90°,
在Rt△PMO中,OM=OD=CD=2,
∴sin∠OPM==,
∴要∠OPM最大,则OP最短,
即OP⊥AE,
如图2,延长DC交直线AE于G,
∵四边形ABCD是矩形,
∴∠B=90°=∠ECG,AB∥CD,
∴∠BAE=∠G,
∵点E是BC的中点,
∴BE=BC=3,
∴△ABE≌△GCE(AAS),
∴CG=AB=4,
∵CD是⊙O的直径,
∴OC=CD=2,
∴OG=OC+CE=6,
在Rt△ABE中,AB=4,BE=3,
∴AE=5,
∵∠OPG=90°=∠B,∠G=∠BAE,
∴△ABE∽△GPO,
∴,
∴,
∴OP=,
在Rt△PMO中,PM===,
故答案为:.
三.解答题
17.证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=∠CAB,
∵BD是⊙O的切线,
∴∠CBD=∠BAE,
∴∠CBD=∠CAB.
18.(1)证明:连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵CP=CB,
∴∠CPB=∠CBP,
∵∠CPB=∠APO,
∴∠CBP=∠APO,
在Rt△AOP中,∵∠A+∠APO=90°,
∴∠OBA+∠CBP=90°,
即:∠OBC=90°,
∴OB⊥CB,
又∵OB是半径,
∴CB与⊙O相切;
(2)解:∵∠A=22.5°,∠AOP=90°,
∴∠APO=67.5°,
∴∠BPC=∠APO=67.5°,
∵PC=CB,
∴∠CBP=67.5°,
∴∠PCB=180°﹣2∠CBP=45°,
∴∠OCB=∠POB=45°,
∴OB=BC=2,
∴图中阴影部分的面积=S△OBC﹣S扇形OBD=×2×2﹣=2﹣.
19.解:(1)PA是⊙O的切线,理由如下:
如图,连接OA,
∴OP是⊙M的直径,点A是⊙M上一点,
∴∠OAP=90°,
即OA⊥PA,
∴PA是⊙O的切线;
(2)设⊙O与OP的交点为N,AB与OP的交点为E,
连接AN,AM,BM,
∵MA=MB,OA=OB,
∴OP是线段AB的垂直平分线,
∴AB⊥OP,AE=BE,
∵OP=9,OA=3,
∴AP==6,
∴S△OAP=OA?AP=AE?OP,
∴OA?AP=AE?OP,
∴3×6=9AE,
∴AE=2,
∴AB=4.
20.(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP==4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
21.解:(1)如图,过点I2作I2Q⊥AC于点Q,连接I2S,
过点I1作I1M⊥BC于点M,I1
N⊥AC于点N,交I2S于点H,
可得四边形QCSl2,I1MCN均为正方形,I1HSM为矩形,
设⊙I2的半径为R,
则AQ=AP=3﹣R,CS=CQ=R,
又因为BP=BS,
所以5+3﹣R=4+R,
解得R=2.
(2)∵∠ACB=90°,AC=3,BC=4,
∴AB==5,
∵I1为△ABC内切圆的圆心,
∴I1M=I1N=,
∴I1
H=3,
∴I1l2==.
22.(1)证明:连接OC,
∵DC切⊙O于C,
∴OC⊥CD,
∵AE⊥CD,
∴AE∥OC,
∵AO=BO,
∴EC=BC,
∴OC=AE,
∵OC=OA=OB=AB,
∴AE=AB;
(2)解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACE=90°,AC⊥BE,
∵由(1)知:AB=AE,
∴EC=BC,
∵BC=16,
∴EC=16,
在RtACB中,由勾股定理得:AC===15,
在Rt△ACE中,S△ACE==,
∵AE=BC=20,
∴=CD,
解得:CD=12,
23.(1)证明:在⊙O中,OB=OD,∠BAC=∠BED,
∴∠ODB=∠OBD,
∵∠DBC=∠BAC,
∴∠DBC=∠BED,
∵DE是⊙O的直径,
∴∠DBE=90°,
∴∠ODB+∠BED=90°,
∴∠OBD+∠DBC=90°,
∴OB⊥BC,
∵OB是⊙O的半径,
∴CB是⊙O的切线;
(2)证明:在⊙O中,∠ABD=∠AED,
由(1)得:∠DBC=∠BED,
∴∠ABD+∠DBC=∠AED+∠BED,
∴∠ABC=∠BEA,
∵DE是⊙O的直径,
∴∠EAC=90°,
∵∠ACB=90°,
∴∠EAC+∠ACB=180°,
∴AE∥BC,
∴∠ABC=∠BAE,
∴∠BEA=∠BAE,
∴AB=EB;
(3)解:延长BO交AE于H,
由∠HAC=∠ACB=∠OBC=90°,得四边形ACBH是矩形,
∴OH⊥AE,
∴BC=AH=AE,
∵DF=3,EF=7,
∴直径DE=10,
即半径DO=EO=5,
∴OF=2,
∵OB∥AC,
∴=,
∴AD=,
在Rt△ADE中,AE==,
∴BC=AH=AE=.
