2020-2021学年八年级数学浙教版下册 课件2.3一元二次方程应用(2)(33张)
文档属性
| 名称 | 2020-2021学年八年级数学浙教版下册 课件2.3一元二次方程应用(2)(33张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 436.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 00:00:00 | ||
图片预览










文档简介
2.3 一元二次方程的应用(2)
探索面积问题,移动问题
教学目标:
1、继续探索一元二次方程的实际应用,进一步体验一元二次方程的应用 价值.
2、进一步掌握列一元二次方程解应用题.的方法和技能.
重点难点:
1、重点:继续探索一元二次方程的应用.
2、难点:“合作学习”的问题较为复杂,计算量大.
列方程解应用题有哪些步骤?
一元二次方程的应用(1)
利润和增长率问题
回顾:
理解问题:审题;找出题中的有关的量;
找出所涉及的基本数量关系;
制订计划:找出本题中作为列方程直接依据的相等关系;
设元(分直接和间接设);用代数式表示有关的量.
执行计划:列方程(关键);解方程(可稍简);
回顾:检验方程的根是否解答正确及是否符合实际意义(细节处)
并作答.
1.用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.
思考:
解:设这个矩形的长为xcm,则宽为 cm,
即
x2-10x+30=0
这里a=1,b=-10,c=30,
∴此方程无实数解.
∴用20cm长的铁丝不能折成面积为30cm2的矩形.
面积问题
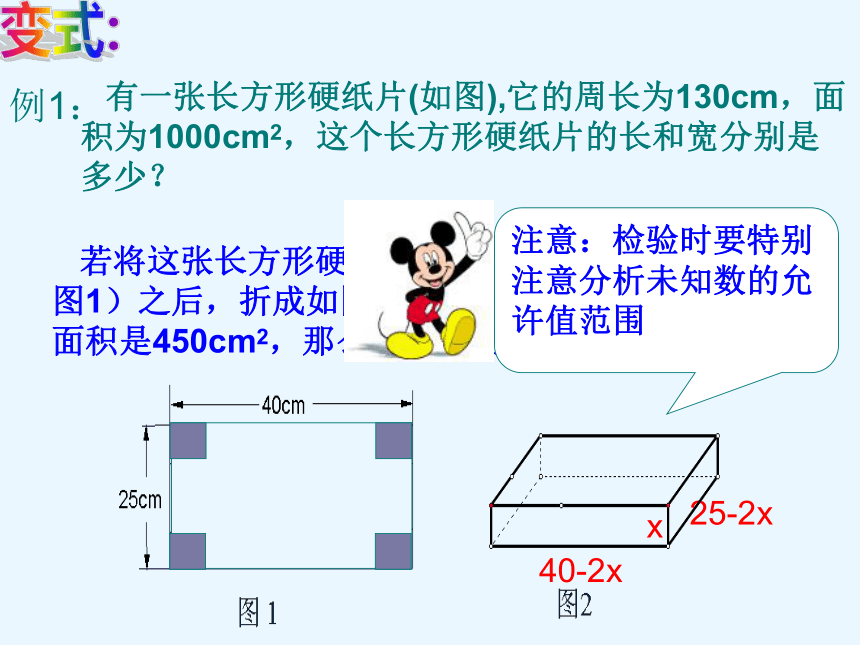
2.有一张长方形硬纸片(如图),它的周长为130cm,面积为1000cm2,这个长方形硬纸片的长和宽分别是多少?
x
解:设一边长为xcm,则另一边长为(65-x)cm
由题意得 x(65-x)=1000
解得 x1=25,x2=40
当x=25时,65-25=40
当x=40时,65-40=25
答:这个长方形硬纸片的长是40厘米,宽是25厘米.
若将这张长方形硬纸片裁去角上四个小正方形(如图1)之后,折成如图2那样的无盖纸盒,若纸盒的底面积是450cm2,那么纸盒的高是多少?
有一张长方形硬纸片(如图),它的周长为130cm,面积为1000cm2,这个长方形硬纸片的长和宽分别是多少?
x
40-2x
25-2x
注意:检验时要特别注意分析未知数的允许值范围
变式:
例1:
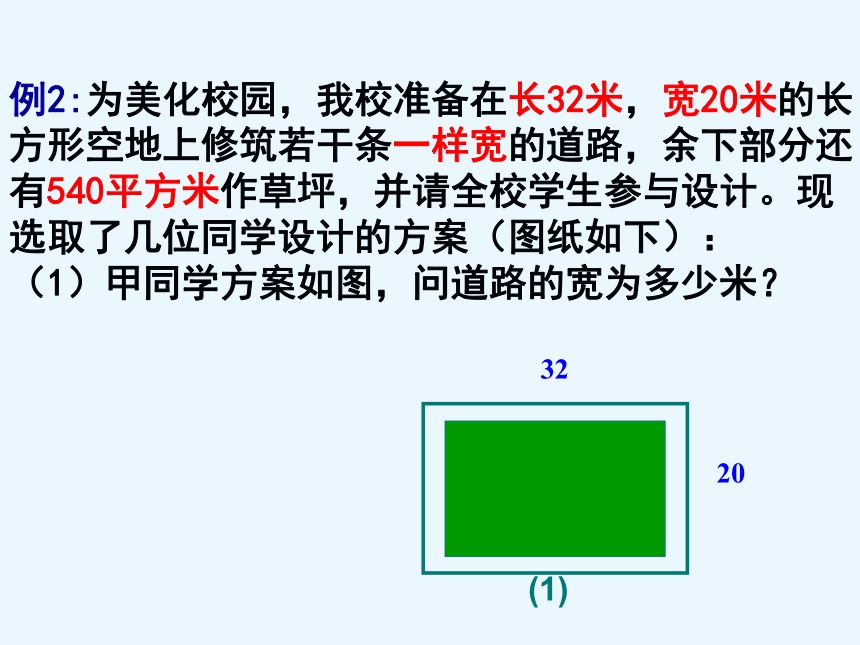
例2:为美化校园,我校准备在长32米,宽20米的长方形空地上修筑若干条一样宽的道路,余下部分还有540平方米作草坪,并请全校学生参与设计。现选取了几位同学设计的方案(图纸如下):
(1)甲同学方案如图,问道路的宽为多少米?
32
20
(1)
(1)
解:(1)如图,设道路的宽为x米,则
化简得,
其中的 x=25超出了原矩形的宽,应舍去.
∴图(1)中道路的宽为1米.
32
20
例2:为美化校园,我校准备在长32米,宽20米的长方形空地上修筑若干条一样宽的道路,余下部分还有540平方米作草坪,并请全校学生参与设计。现选取了几位同学设计的方案(图纸如下):
(2)乙同学方案如图,问道路的宽为多少米?
32
20
则横向的路面面积为 ,
分析:此题的相等关系是矩形面积减去道路面积等于540米2。
解法一、 如图,设道路的宽为x米,
32x 米2
纵向的路面面积为 。
20x 米2
注意:这两个面积的重叠部分是 x2 米2
所列的方程是不是
?
图中的道路面积不是
米2。
(2)
而是从其中减去重叠部分,即应是
米2
化简得,
其中的 x=50超出了原矩形的长和宽,应舍去.
答:所求道路的宽为2米。
解:设路宽为x米,由题意,得
如图,设路宽为x米,
草坪矩形的长(横向)
为 ,
草坪矩形的宽(纵向)为 .
相等关系是:草坪长×草坪宽=540米2
(20-x)米
(32-x)米
化简得:
32
20
(不合题意,舍去)
解:设路宽为x米,则草坪长为(32-x)米,宽为 (20-x)米,由题意,得
答:所求道路的宽为2米。
(3)若把乙同学的道路由直路改为斜路,那么道路的宽又是多少米? (列出方程,不用求解)
32
20
32
(4)若把乙同学的道路由直路改为折路,那么道路的宽又是多少米? (列出方程,不用求解)
20
思考:曲路?
32
20
(5)若选取丙同学方案(如图),则道路的宽又为多少米?(列出方程,不用求解)
思考:你能推广到若干条吗?
解:设道路宽为x米,则草坪长为(32-2x)米,宽为 (20-x)米,由题意,得
总结:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)
(移动问题):
课本第44页作业题第5题
如图,在△ABC中,∠B=90o。点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P、Q分别从A,B同时出发,经过几秒,△PBQ的面积等于8cm2 ?
最大
如图,已知在△ABC中,∠B=90°,AB=28cm,BC=28cm,点P从点A开始沿AB边向点B以3cm/s的速度移动,点Q从点B开始沿BC边向点C以1cm/s的速度移动,P,Q分别从A,B同时出发,
t
3t
28-3t
(2)几秒后,PQ的长度等于14 cm?
(列出方程,不用求解)
变式1:
如图,已知在△ABC中,∠B=90°,AB=28cm,BC=28cm,点P从点A开始沿AB边向点B以3cm/s的速度移动,点Q从点B开始沿BC边向点C以1cm/s的速度移动,P,Q分别从A,B同时出发,
t
3t
28-3t
(3)过Q作QD∥AB交AC于点D,连结PD,求2秒后梯形BQDP的面积。
28-t
28-t
S
梯形BQDP
=26
变式2:
如图,已知在△ABC中,∠B=90°,AB=28cm,BC=28cm,点P从点A开始沿AB边向点B以3cm/s的速度移动,点Q从点B开始沿BC边向点C以1cm/s的速度移动,P,Q分别从A,B同时出发,
t
3t
28-3t
28-t
28-t
(4)过Q作QD∥AB交AC于点D,连结PD,运动几秒梯形BQDP的面积最大?最大面积是多少?
变式3:
小结:
1.面积类相关应用题
2.移动类相关应用题
作业
1、作业本(2)2.3(2)
2、课特2.3(2)(分层选题)基础+提高;提高+拓展.
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
C1
B1
船会受影响吗?
请你带着以下问题和你的伙伴一起合作学习
(1)若接到台风警报t时后,轮船到达C1,台风中心到达B1,当B1C1符合什么条件时船刚好受到台风影响?
合作
学习
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
(2)如果轮船不改变航向,2小时后轮船与台风中心相距多少千米?(精确到1千米)此时轮船有受到台风影响吗?
C1
B1
船会受影响吗?
答:2小时后轮船与台风中心相距428千米,此时轮船没有受到台风影响。
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
(3)如果轮船不改变航向,轮船会不会进入台风影响区?你采用什么方法来判断?
船会受影响吗?
C1
B1
问:这方程解得的t1,t2的实际意义是什么?
t1=8.35
t2=19.34
轮船受台风影响示意图:
由图可知,当t=8.35时,船刚进入台风圈,当t2=19.34时,船即将离开台风圈。
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
C1
B1
船会受影响吗?
合作
学习
(4)如果已知轮船会进入台风影响区,那么请思考轮船受台风影响的时间有多长?
t1=8.35
t2=19.34
轮船受台风影响示意图:
由图可知,当t=8.35时,船刚进入台风圈,当t2=19.34时,船即将离开台风圈,所以影响的时间为19.34-8.35=10.99时。
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
C1
B1
船会受影响吗?
合作
学习
(5)如果把航速改为10km/h ,结果又将怎样?
课本第44页作业题第6题
(实际操作):
如图,要从一块等腰直角三角形白铁皮零料上裁出一块长方形白铁皮。已知AB=AC=20cm,要求裁出的长方形白铁皮的面积为75cm2,应怎样裁?
A
C
B
课本第44页作业题第6题
开放一练:
要从一块等腰直角三角形白铁皮零料上裁出一块长方形白铁皮。已知AB=AC=20cm,要求裁出的长方形白铁皮的面积为75cm2,应怎样裁?
A
B
C
D
E
F
D
E
F
G
A
B
C
D
E
F
G
X
X
X
X
20-X
练一练:
课本第43页作业题第3题
取一张长与宽之比为5:2的长方形纸板,剪去四个边长为5cm的小正方形(如图),并用它做一个无盖的长方体形状的包装盒。要使包装盒的容积为200cm3(纸板的厚度略去不计),问这张长方形纸板的长与宽分别为多少cm?
O
A
B
C
P
Q
如图,AO=BO=50cm,OC是射线,蚂蚁甲以2cm/s的速度从A爬到B,蚂蚁乙以3cm/s的速度从O到C,问:经过几秒两只蚂蚁和O点围成的三角形的面积为450cm2?
探索面积问题,移动问题
教学目标:
1、继续探索一元二次方程的实际应用,进一步体验一元二次方程的应用 价值.
2、进一步掌握列一元二次方程解应用题.的方法和技能.
重点难点:
1、重点:继续探索一元二次方程的应用.
2、难点:“合作学习”的问题较为复杂,计算量大.
列方程解应用题有哪些步骤?
一元二次方程的应用(1)
利润和增长率问题
回顾:
理解问题:审题;找出题中的有关的量;
找出所涉及的基本数量关系;
制订计划:找出本题中作为列方程直接依据的相等关系;
设元(分直接和间接设);用代数式表示有关的量.
执行计划:列方程(关键);解方程(可稍简);
回顾:检验方程的根是否解答正确及是否符合实际意义(细节处)
并作答.
1.用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.
思考:
解:设这个矩形的长为xcm,则宽为 cm,
即
x2-10x+30=0
这里a=1,b=-10,c=30,
∴此方程无实数解.
∴用20cm长的铁丝不能折成面积为30cm2的矩形.
面积问题
2.有一张长方形硬纸片(如图),它的周长为130cm,面积为1000cm2,这个长方形硬纸片的长和宽分别是多少?
x
解:设一边长为xcm,则另一边长为(65-x)cm
由题意得 x(65-x)=1000
解得 x1=25,x2=40
当x=25时,65-25=40
当x=40时,65-40=25
答:这个长方形硬纸片的长是40厘米,宽是25厘米.
若将这张长方形硬纸片裁去角上四个小正方形(如图1)之后,折成如图2那样的无盖纸盒,若纸盒的底面积是450cm2,那么纸盒的高是多少?
有一张长方形硬纸片(如图),它的周长为130cm,面积为1000cm2,这个长方形硬纸片的长和宽分别是多少?
x
40-2x
25-2x
注意:检验时要特别注意分析未知数的允许值范围
变式:
例1:
例2:为美化校园,我校准备在长32米,宽20米的长方形空地上修筑若干条一样宽的道路,余下部分还有540平方米作草坪,并请全校学生参与设计。现选取了几位同学设计的方案(图纸如下):
(1)甲同学方案如图,问道路的宽为多少米?
32
20
(1)
(1)
解:(1)如图,设道路的宽为x米,则
化简得,
其中的 x=25超出了原矩形的宽,应舍去.
∴图(1)中道路的宽为1米.
32
20
例2:为美化校园,我校准备在长32米,宽20米的长方形空地上修筑若干条一样宽的道路,余下部分还有540平方米作草坪,并请全校学生参与设计。现选取了几位同学设计的方案(图纸如下):
(2)乙同学方案如图,问道路的宽为多少米?
32
20
则横向的路面面积为 ,
分析:此题的相等关系是矩形面积减去道路面积等于540米2。
解法一、 如图,设道路的宽为x米,
32x 米2
纵向的路面面积为 。
20x 米2
注意:这两个面积的重叠部分是 x2 米2
所列的方程是不是
?
图中的道路面积不是
米2。
(2)
而是从其中减去重叠部分,即应是
米2
化简得,
其中的 x=50超出了原矩形的长和宽,应舍去.
答:所求道路的宽为2米。
解:设路宽为x米,由题意,得
如图,设路宽为x米,
草坪矩形的长(横向)
为 ,
草坪矩形的宽(纵向)为 .
相等关系是:草坪长×草坪宽=540米2
(20-x)米
(32-x)米
化简得:
32
20
(不合题意,舍去)
解:设路宽为x米,则草坪长为(32-x)米,宽为 (20-x)米,由题意,得
答:所求道路的宽为2米。
(3)若把乙同学的道路由直路改为斜路,那么道路的宽又是多少米? (列出方程,不用求解)
32
20
32
(4)若把乙同学的道路由直路改为折路,那么道路的宽又是多少米? (列出方程,不用求解)
20
思考:曲路?
32
20
(5)若选取丙同学方案(如图),则道路的宽又为多少米?(列出方程,不用求解)
思考:你能推广到若干条吗?
解:设道路宽为x米,则草坪长为(32-2x)米,宽为 (20-x)米,由题意,得
总结:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)
(移动问题):
课本第44页作业题第5题
如图,在△ABC中,∠B=90o。点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P、Q分别从A,B同时出发,经过几秒,△PBQ的面积等于8cm2 ?
最大
如图,已知在△ABC中,∠B=90°,AB=28cm,BC=28cm,点P从点A开始沿AB边向点B以3cm/s的速度移动,点Q从点B开始沿BC边向点C以1cm/s的速度移动,P,Q分别从A,B同时出发,
t
3t
28-3t
(2)几秒后,PQ的长度等于14 cm?
(列出方程,不用求解)
变式1:
如图,已知在△ABC中,∠B=90°,AB=28cm,BC=28cm,点P从点A开始沿AB边向点B以3cm/s的速度移动,点Q从点B开始沿BC边向点C以1cm/s的速度移动,P,Q分别从A,B同时出发,
t
3t
28-3t
(3)过Q作QD∥AB交AC于点D,连结PD,求2秒后梯形BQDP的面积。
28-t
28-t
S
梯形BQDP
=26
变式2:
如图,已知在△ABC中,∠B=90°,AB=28cm,BC=28cm,点P从点A开始沿AB边向点B以3cm/s的速度移动,点Q从点B开始沿BC边向点C以1cm/s的速度移动,P,Q分别从A,B同时出发,
t
3t
28-3t
28-t
28-t
(4)过Q作QD∥AB交AC于点D,连结PD,运动几秒梯形BQDP的面积最大?最大面积是多少?
变式3:
小结:
1.面积类相关应用题
2.移动类相关应用题
作业
1、作业本(2)2.3(2)
2、课特2.3(2)(分层选题)基础+提高;提高+拓展.
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
C1
B1
船会受影响吗?
请你带着以下问题和你的伙伴一起合作学习
(1)若接到台风警报t时后,轮船到达C1,台风中心到达B1,当B1C1符合什么条件时船刚好受到台风影响?
合作
学习
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
(2)如果轮船不改变航向,2小时后轮船与台风中心相距多少千米?(精确到1千米)此时轮船有受到台风影响吗?
C1
B1
船会受影响吗?
答:2小时后轮船与台风中心相距428千米,此时轮船没有受到台风影响。
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
(3)如果轮船不改变航向,轮船会不会进入台风影响区?你采用什么方法来判断?
船会受影响吗?
C1
B1
问:这方程解得的t1,t2的实际意义是什么?
t1=8.35
t2=19.34
轮船受台风影响示意图:
由图可知,当t=8.35时,船刚进入台风圈,当t2=19.34时,船即将离开台风圈。
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
C1
B1
船会受影响吗?
合作
学习
(4)如果已知轮船会进入台风影响区,那么请思考轮船受台风影响的时间有多长?
t1=8.35
t2=19.34
轮船受台风影响示意图:
由图可知,当t=8.35时,船刚进入台风圈,当t2=19.34时,船即将离开台风圈,所以影响的时间为19.34-8.35=10.99时。
一轮船以30 km/h的速度由西向东航行(如图),在途中接到台风警报,台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 Km的区域(包括边界)都属于受台风影响区。当轮船接到台风警报时,测得BC=500km,BA=300km
C1
B1
船会受影响吗?
合作
学习
(5)如果把航速改为10km/h ,结果又将怎样?
课本第44页作业题第6题
(实际操作):
如图,要从一块等腰直角三角形白铁皮零料上裁出一块长方形白铁皮。已知AB=AC=20cm,要求裁出的长方形白铁皮的面积为75cm2,应怎样裁?
A
C
B
课本第44页作业题第6题
开放一练:
要从一块等腰直角三角形白铁皮零料上裁出一块长方形白铁皮。已知AB=AC=20cm,要求裁出的长方形白铁皮的面积为75cm2,应怎样裁?
A
B
C
D
E
F
D
E
F
G
A
B
C
D
E
F
G
X
X
X
X
20-X
练一练:
课本第43页作业题第3题
取一张长与宽之比为5:2的长方形纸板,剪去四个边长为5cm的小正方形(如图),并用它做一个无盖的长方体形状的包装盒。要使包装盒的容积为200cm3(纸板的厚度略去不计),问这张长方形纸板的长与宽分别为多少cm?
O
A
B
C
P
Q
如图,AO=BO=50cm,OC是射线,蚂蚁甲以2cm/s的速度从A爬到B,蚂蚁乙以3cm/s的速度从O到C,问:经过几秒两只蚂蚁和O点围成的三角形的面积为450cm2?
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
