2020-2021学年浙教版八年级下册数学课件2.4一元二次方程根与系数(15张)
文档属性
| 名称 | 2020-2021学年浙教版八年级下册数学课件2.4一元二次方程根与系数(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 114.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 00:00:00 | ||
图片预览




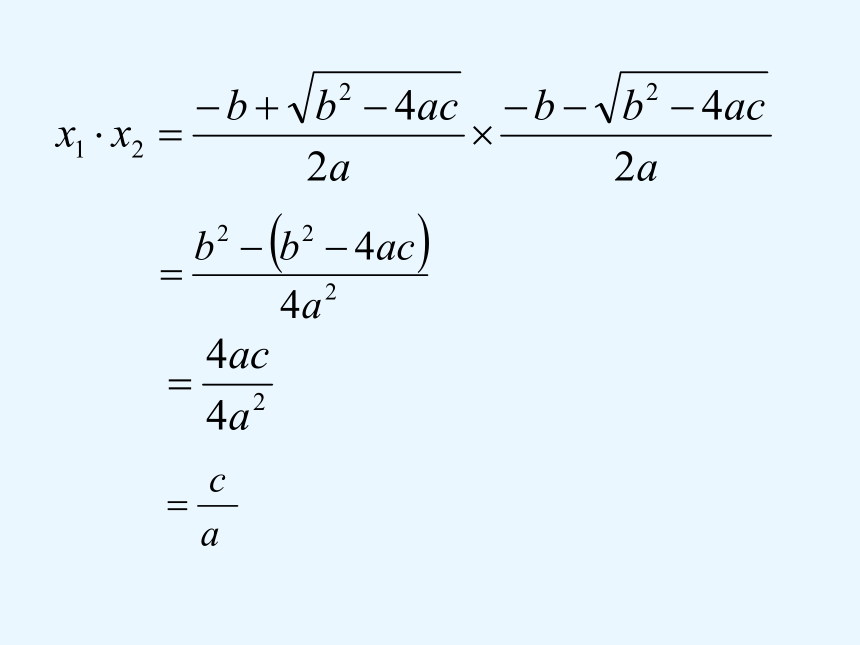


文档简介
2.4 一元二次方程根与系数的关系
教学目标:
1、经历一元二次方程根与系数的关系的发现过程.
2、了解一元二次方程根与系数的关系与证明.
3、会运用一元二次方程根与系数的关系简化一元二次方程根的运算.
重点难点:
1、重点:一元二次方程根与系数的关系.
2、难点:例2的解题思路不易形成.
1.一元二次方程的一般形式是什么?
3.一元二次方程的根的情况怎样确定?
2.一元二次方程的求根公式是什么?
复习回顾
推导:
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
1.已知一元二次方程x2+3x+1=0的两根分别为x1,x2 ,则:x1+x2=____, x1x2=____.
3.已知一元二次方程3x2-9x+m=0的一个根为1 ,则方程的另一根为_____,m=_____.
4.已知一元二次方程x2+px+q=0的两根分别为 -2和1,则p=_____; q=______.
2.已知一元二次方程2x2-3x-5=0的两根分别为x1,x2 ,则:x1+x2=____, x1x2=____.
练习:
例1、设x1,x2 是一元二次方程5x2-7x-3=0的两根,求下列式子的值:
应用一:求含有两根的代数式的值
(3)x13x2+x1x23
(4)
(5)(x1-x2)2
例2: 已知一个一元二次方程的二次项系数是3,它的两个根分别是 ,1.
写出这个方程.
课本P46 T6
应用二:已知两根求一元二次方程
应用三:已知一根求另一根和未知系数的值
例3:已知方程 的一个根是 ,
求它的另一个根及k的值.
练习:方程x2?(m?1)x?2m?1?0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
练习:P46作业题T4,T5
2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式.
3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,
即在 初中代数里,当且仅当△≥0时,
才能应用根与系数的关系.
1.一元二次方程根与系数的关系:
小结
作业
1、作业本(2)2.3(2)
2、课特2.3(2)(分层选题)基础+提高;提高+拓展.
探索:
两根均为负的条件: X1+X2 且X1X2 。
两根均为正的条件: X1+X2 且X1X2 。
两根一正一负的条件: X1+X2 且X1X2 。
当然,以上还必须满足一元二次方程有根的条件:b2-4ac≥0
引申:1、若ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,则b?0;
(2)若两根互为倒数,则a?c;
(3)若一根为0,则c?0 ;
(4)若一根为1,则a?b?c?0 ;
(5)若一根为?1,则a?b?c?0;
(6)若a、c异号,方程一定有两个实数根.
教学目标:
1、经历一元二次方程根与系数的关系的发现过程.
2、了解一元二次方程根与系数的关系与证明.
3、会运用一元二次方程根与系数的关系简化一元二次方程根的运算.
重点难点:
1、重点:一元二次方程根与系数的关系.
2、难点:例2的解题思路不易形成.
1.一元二次方程的一般形式是什么?
3.一元二次方程的根的情况怎样确定?
2.一元二次方程的求根公式是什么?
复习回顾
推导:
如果一元二次方程
的两个根分别是 、 ,那么:
这就是一元二次方程根与系数的关系,也叫韦达定理。
1.已知一元二次方程x2+3x+1=0的两根分别为x1,x2 ,则:x1+x2=____, x1x2=____.
3.已知一元二次方程3x2-9x+m=0的一个根为1 ,则方程的另一根为_____,m=_____.
4.已知一元二次方程x2+px+q=0的两根分别为 -2和1,则p=_____; q=______.
2.已知一元二次方程2x2-3x-5=0的两根分别为x1,x2 ,则:x1+x2=____, x1x2=____.
练习:
例1、设x1,x2 是一元二次方程5x2-7x-3=0的两根,求下列式子的值:
应用一:求含有两根的代数式的值
(3)x13x2+x1x23
(4)
(5)(x1-x2)2
例2: 已知一个一元二次方程的二次项系数是3,它的两个根分别是 ,1.
写出这个方程.
课本P46 T6
应用二:已知两根求一元二次方程
应用三:已知一根求另一根和未知系数的值
例3:已知方程 的一个根是 ,
求它的另一个根及k的值.
练习:方程x2?(m?1)x?2m?1?0求m满足什么条件时,方程的两根互为相反数?方程的两根互为倒数?方程的一根为零?
练习:P46作业题T4,T5
2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式.
3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,
即在 初中代数里,当且仅当△≥0时,
才能应用根与系数的关系.
1.一元二次方程根与系数的关系:
小结
作业
1、作业本(2)2.3(2)
2、课特2.3(2)(分层选题)基础+提高;提高+拓展.
探索:
两根均为负的条件: X1+X2 且X1X2 。
两根均为正的条件: X1+X2 且X1X2 。
两根一正一负的条件: X1+X2 且X1X2 。
当然,以上还必须满足一元二次方程有根的条件:b2-4ac≥0
引申:1、若ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,则b?0;
(2)若两根互为倒数,则a?c;
(3)若一根为0,则c?0 ;
(4)若一根为1,则a?b?c?0 ;
(5)若一根为?1,则a?b?c?0;
(6)若a、c异号,方程一定有两个实数根.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
