2020-2021学年浙教版八年级数学下册课件2.2 用公式法解一元二次方程(4)(18张)
文档属性
| 名称 | 2020-2021学年浙教版八年级数学下册课件2.2 用公式法解一元二次方程(4)(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 398.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 20:14:39 | ||
图片预览





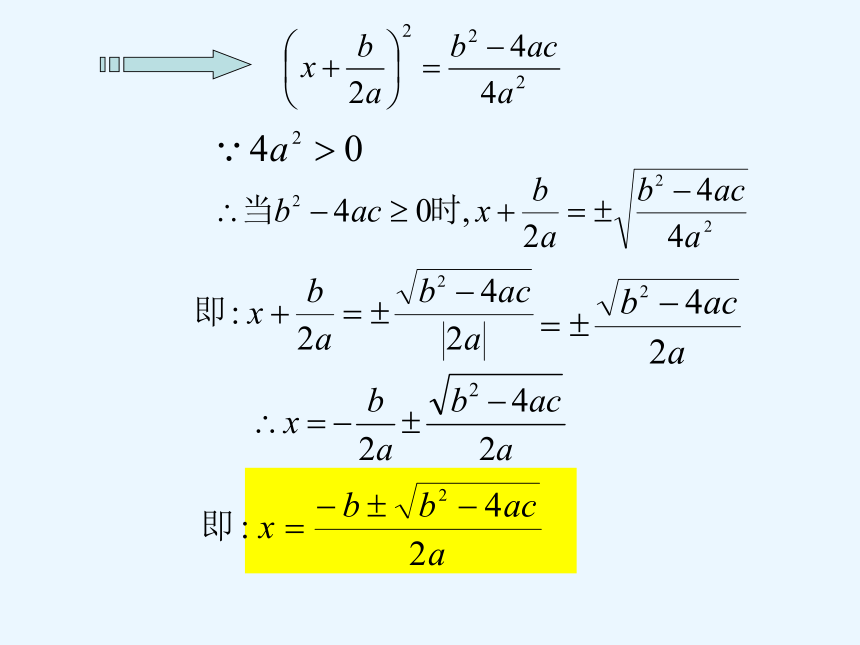
文档简介
2.2一元二次方程的解法(4)
教学目标:
1、理解一元二次方程求根公式的推导过程.
2、会用一元二次方程根的判别式判定一元二次方程的根的情况.
3、会用公式法解一元二次方程.
重点难点:
1、重点:用公式法解一元二次方程.
2、难点:一元二次方程的求根公式的推导过程比较复杂,涉及多方面的知识和能力,是本节课的教学难点.
温故知新
配方法
因式分解法
开平方法
学过哪些解一元二次方程的解法?
用配方法解一元二次方程的一般步骤:
(1)把二次项系数化为1;
(2)方程两边同时加上一次项
系数一半的平方;
(3)把方程化成x2=a的形式;
(4)用开平方法解方程。
已知9x2 + 18(n-1)x + 18n是一个关于x的
完全平方式,求常数n的值。
公式的推导
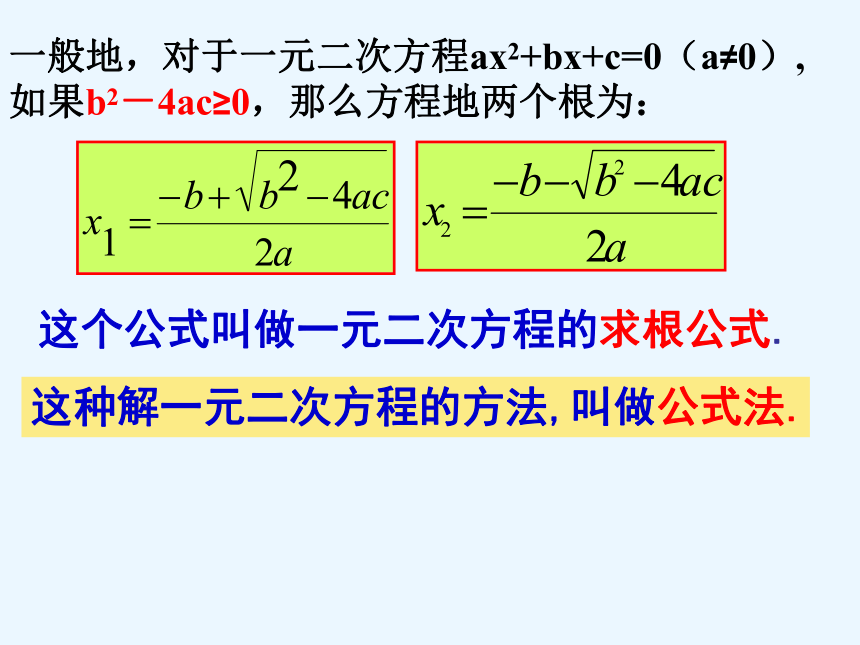
一般地,对于一元二次方程ax2+bx+c=0(a≠0),
如果b2-4ac≥0,那么方程地两个根为:
这个公式叫做一元二次方程的求根公式.
这种解一元二次方程的方法,叫做公式法.
例8 用公式法解下列一元二次方程:
(1)2x2 -5x+ 3 = 0
(2)4x2 +1 =-4x
小 结:
对于 (a≠0)
有两个不相同的实数根
有两个相同的实数根
无实数根
用求根公式解一元二次方程的流程图
确定a, b, c 的值
计算b2-4ac
b2-4ac ≥0
是
否
方程无实数根
理一理
解: 方程的两边同乘4,得
3x2–8x-2=0,
∴a=3,b=-8,c=-2,
b?-4ac=(-8)?-4×3×(-2)=88
∴ x1= , x2=
例8 用公式法解下列一元二次方程:
解方程:
解 :去括号,得 x2–x = x2–4x+4
化简,得 x2 – 3x+4 =0
∴a= ,b=-3,c=4,
b?-4ac=(-3)?-4× ×4=1
∴ x1= 4 , x2=2
例9:
(请用多种方法)
解方程:
解 :整理,得 x(x –2)= (x-2)2
移项,得 (x-2)2 – x( x-2) =0
分解因式,得(x-2)(x-2 - x) =0
即 (x-2)( x-2) =0
∴x-2=0 或 x-2=0
∴ x1= 2 , x2=4
例9:
选择合适的方法解下列方程:
?
?
(1)
(2)
(3)
(4)
拓展提高
1、如果一元二次方程2x2-x+m=0有两个不相等的实数根,则m的取值范围为 。
2、三角形每条边的长都是方程x2-6x+8=0的根,求该三角形的周长。
3、已知x2+x-1=0,求代数式x3+2x2-7的值。
4.试用一元二次方程的求根公式探索方程 : ax2+bx+c=0(a≠0)
(1)两根互为相反数的条件是______;
(2)两根互为倒数的条件是______.
b=0
a=c
x1+x2=0
x1×x2=1
提高拓展
作业
1、作业本2.2(4)
2、课时2.2(4)
B层(基础+提高)
A层(提高+综合)
2.2(4)一元二次方程的解法
投影屏幕
公式法
例题
练习
步骤
……………………
……………
求根公式
……………………
……………
……………………
……………
板书设计
教学目标:
1、理解一元二次方程求根公式的推导过程.
2、会用一元二次方程根的判别式判定一元二次方程的根的情况.
3、会用公式法解一元二次方程.
重点难点:
1、重点:用公式法解一元二次方程.
2、难点:一元二次方程的求根公式的推导过程比较复杂,涉及多方面的知识和能力,是本节课的教学难点.
温故知新
配方法
因式分解法
开平方法
学过哪些解一元二次方程的解法?
用配方法解一元二次方程的一般步骤:
(1)把二次项系数化为1;
(2)方程两边同时加上一次项
系数一半的平方;
(3)把方程化成x2=a的形式;
(4)用开平方法解方程。
已知9x2 + 18(n-1)x + 18n是一个关于x的
完全平方式,求常数n的值。
公式的推导
一般地,对于一元二次方程ax2+bx+c=0(a≠0),
如果b2-4ac≥0,那么方程地两个根为:
这个公式叫做一元二次方程的求根公式.
这种解一元二次方程的方法,叫做公式法.
例8 用公式法解下列一元二次方程:
(1)2x2 -5x+ 3 = 0
(2)4x2 +1 =-4x
小 结:
对于 (a≠0)
有两个不相同的实数根
有两个相同的实数根
无实数根
用求根公式解一元二次方程的流程图
确定a, b, c 的值
计算b2-4ac
b2-4ac ≥0
是
否
方程无实数根
理一理
解: 方程的两边同乘4,得
3x2–8x-2=0,
∴a=3,b=-8,c=-2,
b?-4ac=(-8)?-4×3×(-2)=88
∴ x1= , x2=
例8 用公式法解下列一元二次方程:
解方程:
解 :去括号,得 x2–x = x2–4x+4
化简,得 x2 – 3x+4 =0
∴a= ,b=-3,c=4,
b?-4ac=(-3)?-4× ×4=1
∴ x1= 4 , x2=2
例9:
(请用多种方法)
解方程:
解 :整理,得 x(x –2)= (x-2)2
移项,得 (x-2)2 – x( x-2) =0
分解因式,得(x-2)(x-2 - x) =0
即 (x-2)( x-2) =0
∴x-2=0 或 x-2=0
∴ x1= 2 , x2=4
例9:
选择合适的方法解下列方程:
?
?
(1)
(2)
(3)
(4)
拓展提高
1、如果一元二次方程2x2-x+m=0有两个不相等的实数根,则m的取值范围为 。
2、三角形每条边的长都是方程x2-6x+8=0的根,求该三角形的周长。
3、已知x2+x-1=0,求代数式x3+2x2-7的值。
4.试用一元二次方程的求根公式探索方程 : ax2+bx+c=0(a≠0)
(1)两根互为相反数的条件是______;
(2)两根互为倒数的条件是______.
b=0
a=c
x1+x2=0
x1×x2=1
提高拓展
作业
1、作业本2.2(4)
2、课时2.2(4)
B层(基础+提高)
A层(提高+综合)
2.2(4)一元二次方程的解法
投影屏幕
公式法
例题
练习
步骤
……………………
……………
求根公式
……………………
……………
……………………
……………
板书设计
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
