2020-2021学年浙教版八年级数学下册课件 2.1 一元二次方程(共23张)
文档属性
| 名称 | 2020-2021学年浙教版八年级数学下册课件 2.1 一元二次方程(共23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 790.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 21:25:17 | ||
图片预览








文档简介
(共23张PPT)
第二章
一元二次方程
2.1
一元二次方程
教学目标
1.理解一元二次方程的概念.
2.掌握一元二次方程的一般形式
.
3.掌握一元二次方程的解得概念并会简单应用.
教学重难点
1.本节教学的重点是一元二次方程的概念.
2.一元二次方程的一般形式及解的应用是本节教学的难点.
回顾旧知
判断下列式子是否是一元一次方程:
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
一元一次方程
情境引入
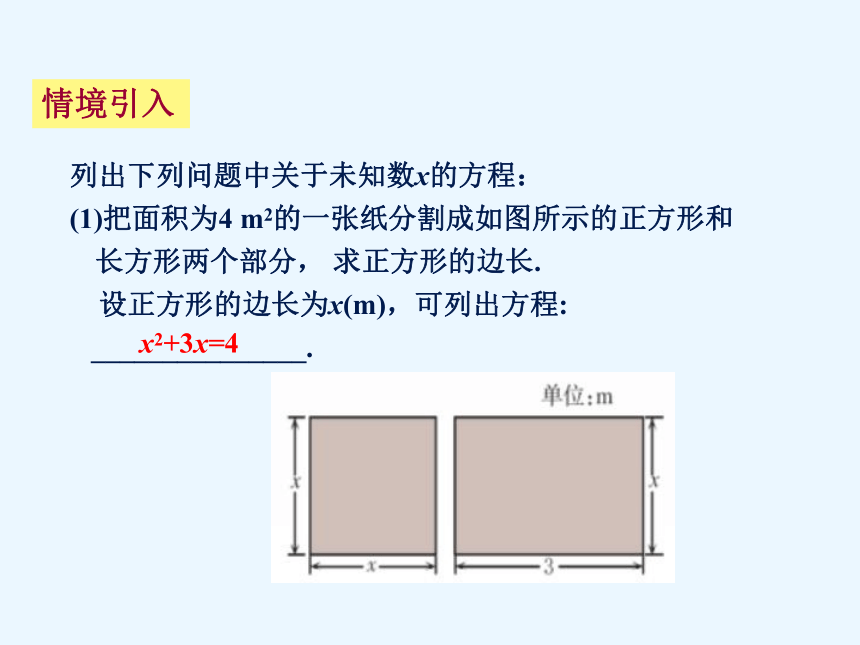
列出下列问题中关于未知数x的方程:
(1)把面积为4
m2的一张纸分割成如图所示的正方形和长方形两个部分,
求正方形的边长.
设正方形的边长为x(m),可列出方程:
_______________.
x2+3x=4
(2)某放射性元素经2天后,质量衰变为原来的
这
种放射性元
素平均每天减少率为多少?
设平均每天减少率为x,
可列出方程:________________.
(1-x)2=
这些方程是一元一次方程吗?如果不是,请说明理由.
这些方程不是一元一次方程,因为它们未知数的指数都为2.
思考
观察上面所列方程,说出这些方程与一元一次方程的相同和不同之处.
相同点:等号两边都是整式,只含有一个未知数.
不同点:一元一次方程的未知数的指数是1次;
而这些方程的未知数的指数是2次。
方程x2+3x=4和(1-x)2=
的两边都是整式,只含
有一个未知数,并且未知数的最高次数是2次.我们把
这样的方程叫做一元二次方程.
总结
1、只有一个未知数
2、未知数的指数是二次
3、方程的两边都是整式
一元二次方程
判断一元二次方程的方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
判断下列方程是否为一元二次方程?
练习
深入探究1
ax2+bx+c=0(a,b,c为常数,a≠0)
b,c可以为零吗?
一元二次方程的一般形式:
a、b、c分别叫做二次项系数、一次项系数和常数项.
下列这个方程还可以怎么表示呢?
一般地,任何一个关于x的一元二次方程都可以化为
,的形式,我们把ax2+bx+c=0
(a,b,c为常数,a≠0)称为一元二次方程的一般形式.
其中ax2,bx,
c
分别称为二次项,一次项,
常数项,a,b
分别称为二次项系数,一次项系数.
为什么要限制a≠0,
b,
c可以为0吗?
想一想
总结
(1)移项,整理,得9x2+4x-5
=
0.
这个方程的二次项系数是9,一次项系数是4,常数项
是-5.
(2)
方程左边多项式相乘,得-3x2
+2x+8
=
3
,
移项,整理,得-3x2
+2x+
5
=
0.
这个方程的二次项系数是-3,一次项系数是2,常数
项是5.
例1
解:
把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
(1)
9x2=5-4x.
(2)
(2-x)(3x+4)
=
3.
去括号,得
3x2-3x=2x-4-4.
移项,合并同类项,得方程的一般形式:
3x2-5x+8=0.
它的二次项系数是3,一次项系数是-5,
常数项是8.
解:
1.
把方程3x(x-1)=2(x-2)-4化成一般形式,
并写出它的二次项系数、一次项系数及常数项.
练习
1.要确定一元二次方程的系数和常数项
,必须先将方程化为一般形式.
2.在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项.
注意
3.若方程中含有整式乘法,要先利用法则展开再进行变形.
4.
一般情况下,二次项系数应化为正数.
根据“常数项为0”这一条件可列出以a为未知数的
方程,求出a的值,同时注意二次项系数不能为0.
导引:
2.
关于x的一元二次方程(a-2)x2+3x+a2-4=0的常数项为0,求a的值.
∵关于x的一元二次方程
(a-2)x2+3x+a2-4=0的常数项为0,
∴
解得a=-2.
解:
练习
1.化一般形式一般要经历一去(去分母、去括号)、二移、三并这三步;
2.当整理为一般形式后,如果二次项系数是负数,一般要把它转化为正数,若有关系数是分数,一般要把它转化为整数.
总结
3.在解由一元二次方程的定义求有关待定字母的值时,
先
要把方程整理成一元二次方程的一般形式,再由题中给出的条件及二次项系数不为零列式求出.
温馨提示:条件中若明确指出该方程是一元二次方程,则隐含“二次项系数不能为零”这一条件,解题时容易漏掉.
能使一元二次方程左右两边相等的未知数的值叫一元二次方程的解(或根).
判断未知数的值x=
-1,x=0,x=2是不是方程x2-2=x的根.
用代入法检验是否为方程的根!
做一做
?
深入探究2
要点精析:
(1)判定某个数是方程的根的必要条件:使方程左右两边相等.
(2)根据方程的根的定义可以判断解出的方程的根是否正确.
(3)一元二次方程的根不止一个,只要符合条件的都是方程的根.
一元二次方程的解(或根)注意一下几点:
将
和x2=
-
3代入方程
得
所以这个一元二次方程是
例2
已知一元二次方程
的两个根为
和x2=
-
3,
求这个方程.
解:
解得
方程的根就是满足方程左右两边相等的未知数
的值,因此求含有字母系数的一元二次方程中的字
母的值时,只需把已知方程的根代入原方程就可求
出相关的待定字母的值.
总结
练习
1、判断下列题括号内未知数的值是不是方程的根:
x2-3x+2=0
(x1=1,x2=2,x3=3)
2、构造一个一元二次方程,要求:
(1)常数项为零;(2)有一根为2
.
3、已知关于x的一元二次方程
x2
+
ax
+
a
=
0的一个根是3,求
a
的值。
课堂小结
1.了解一元二次方程的概念和一般形式.
2.会判别一元二次方程的二次项系数,一次项系数和常数项.
3.了解一元二次方程的解(或根)的概念。
4.注意:一元二次方程的二次项系数不能为零.
拓展练习
已知关于x的一元二次方程
ax2+bx+c=0
(a≠0)的一个根为1,求a+b+c的值.
解:由题意得
思考:若
a+b+c=0,你能通过观察,求出方程ax2+bx+c=0
(a≠0)一个根吗?
解:由题意得
∴方程ax2+bx+c=0
(a≠0)一个根是1.
拓展:若
a-b
+c=0,
你能通过观察,求出方程ax2+bx+c=0
(a≠0)一个根吗?
4a
+
2b
+
c
=0
第二章
一元二次方程
2.1
一元二次方程
教学目标
1.理解一元二次方程的概念.
2.掌握一元二次方程的一般形式
.
3.掌握一元二次方程的解得概念并会简单应用.
教学重难点
1.本节教学的重点是一元二次方程的概念.
2.一元二次方程的一般形式及解的应用是本节教学的难点.
回顾旧知
判断下列式子是否是一元一次方程:
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
一元一次方程
情境引入
列出下列问题中关于未知数x的方程:
(1)把面积为4
m2的一张纸分割成如图所示的正方形和长方形两个部分,
求正方形的边长.
设正方形的边长为x(m),可列出方程:
_______________.
x2+3x=4
(2)某放射性元素经2天后,质量衰变为原来的
这
种放射性元
素平均每天减少率为多少?
设平均每天减少率为x,
可列出方程:________________.
(1-x)2=
这些方程是一元一次方程吗?如果不是,请说明理由.
这些方程不是一元一次方程,因为它们未知数的指数都为2.
思考
观察上面所列方程,说出这些方程与一元一次方程的相同和不同之处.
相同点:等号两边都是整式,只含有一个未知数.
不同点:一元一次方程的未知数的指数是1次;
而这些方程的未知数的指数是2次。
方程x2+3x=4和(1-x)2=
的两边都是整式,只含
有一个未知数,并且未知数的最高次数是2次.我们把
这样的方程叫做一元二次方程.
总结
1、只有一个未知数
2、未知数的指数是二次
3、方程的两边都是整式
一元二次方程
判断一元二次方程的方法:
整理前:①整式方程,②只含一个未知数;
整理后:未知数的最高次数是2.
判断下列方程是否为一元二次方程?
练习
深入探究1
ax2+bx+c=0(a,b,c为常数,a≠0)
b,c可以为零吗?
一元二次方程的一般形式:
a、b、c分别叫做二次项系数、一次项系数和常数项.
下列这个方程还可以怎么表示呢?
一般地,任何一个关于x的一元二次方程都可以化为
,的形式,我们把ax2+bx+c=0
(a,b,c为常数,a≠0)称为一元二次方程的一般形式.
其中ax2,bx,
c
分别称为二次项,一次项,
常数项,a,b
分别称为二次项系数,一次项系数.
为什么要限制a≠0,
b,
c可以为0吗?
想一想
总结
(1)移项,整理,得9x2+4x-5
=
0.
这个方程的二次项系数是9,一次项系数是4,常数项
是-5.
(2)
方程左边多项式相乘,得-3x2
+2x+8
=
3
,
移项,整理,得-3x2
+2x+
5
=
0.
这个方程的二次项系数是-3,一次项系数是2,常数
项是5.
例1
解:
把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.
(1)
9x2=5-4x.
(2)
(2-x)(3x+4)
=
3.
去括号,得
3x2-3x=2x-4-4.
移项,合并同类项,得方程的一般形式:
3x2-5x+8=0.
它的二次项系数是3,一次项系数是-5,
常数项是8.
解:
1.
把方程3x(x-1)=2(x-2)-4化成一般形式,
并写出它的二次项系数、一次项系数及常数项.
练习
1.要确定一元二次方程的系数和常数项
,必须先将方程化为一般形式.
2.在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项.
注意
3.若方程中含有整式乘法,要先利用法则展开再进行变形.
4.
一般情况下,二次项系数应化为正数.
根据“常数项为0”这一条件可列出以a为未知数的
方程,求出a的值,同时注意二次项系数不能为0.
导引:
2.
关于x的一元二次方程(a-2)x2+3x+a2-4=0的常数项为0,求a的值.
∵关于x的一元二次方程
(a-2)x2+3x+a2-4=0的常数项为0,
∴
解得a=-2.
解:
练习
1.化一般形式一般要经历一去(去分母、去括号)、二移、三并这三步;
2.当整理为一般形式后,如果二次项系数是负数,一般要把它转化为正数,若有关系数是分数,一般要把它转化为整数.
总结
3.在解由一元二次方程的定义求有关待定字母的值时,
先
要把方程整理成一元二次方程的一般形式,再由题中给出的条件及二次项系数不为零列式求出.
温馨提示:条件中若明确指出该方程是一元二次方程,则隐含“二次项系数不能为零”这一条件,解题时容易漏掉.
能使一元二次方程左右两边相等的未知数的值叫一元二次方程的解(或根).
判断未知数的值x=
-1,x=0,x=2是不是方程x2-2=x的根.
用代入法检验是否为方程的根!
做一做
?
深入探究2
要点精析:
(1)判定某个数是方程的根的必要条件:使方程左右两边相等.
(2)根据方程的根的定义可以判断解出的方程的根是否正确.
(3)一元二次方程的根不止一个,只要符合条件的都是方程的根.
一元二次方程的解(或根)注意一下几点:
将
和x2=
-
3代入方程
得
所以这个一元二次方程是
例2
已知一元二次方程
的两个根为
和x2=
-
3,
求这个方程.
解:
解得
方程的根就是满足方程左右两边相等的未知数
的值,因此求含有字母系数的一元二次方程中的字
母的值时,只需把已知方程的根代入原方程就可求
出相关的待定字母的值.
总结
练习
1、判断下列题括号内未知数的值是不是方程的根:
x2-3x+2=0
(x1=1,x2=2,x3=3)
2、构造一个一元二次方程,要求:
(1)常数项为零;(2)有一根为2
.
3、已知关于x的一元二次方程
x2
+
ax
+
a
=
0的一个根是3,求
a
的值。
课堂小结
1.了解一元二次方程的概念和一般形式.
2.会判别一元二次方程的二次项系数,一次项系数和常数项.
3.了解一元二次方程的解(或根)的概念。
4.注意:一元二次方程的二次项系数不能为零.
拓展练习
已知关于x的一元二次方程
ax2+bx+c=0
(a≠0)的一个根为1,求a+b+c的值.
解:由题意得
思考:若
a+b+c=0,你能通过观察,求出方程ax2+bx+c=0
(a≠0)一个根吗?
解:由题意得
∴方程ax2+bx+c=0
(a≠0)一个根是1.
拓展:若
a-b
+c=0,
你能通过观察,求出方程ax2+bx+c=0
(a≠0)一个根吗?
4a
+
2b
+
c
=0
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
