第四章 平行四边形单元测试卷(含解析)
文档属性
| 名称 | 第四章 平行四边形单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 716.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-23 16:52:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
八年级下册数学
平行四边形
单元测试卷
(满分100分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列图标中,既是轴对称图形,又是中心对称图形的是(
)
A.
B.
C.
D.
如图,?ABCD中,对角线AC和BD相交于点O,若AC=8,AB=6,BD=m,那么m的取范围是(?
?
)
A.
2<m<10
B.
2<m<14
C.
6<m<8
D.
4<m<20
下列说法正确的是(
)
A.
有两组对边分别平行的图形是平行四边形
B.
平行四边形的对角线相等
C.
平行四边形的对角互补,邻角相等
D.
平行四边形的对边平行且相等
若一个多边形的每个内角都是108°,则这个多边形的内角和为(
)
A.
360°
B.
540°
C.
720°
D.
900°
用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
A.
有一个内角小于90°
B.
每一个内角都大于90°
C.
有一个内角小于或等于90°
D.
每一个内角都小于90°
如图,将?ABCD沿对角线AC折叠,使点B落在B'处.若1=2=,则B为(?
?
)
A.
B.
C.
D.
如图,点E,F是平行四边形ABCD对角线上两点,在条件;;;中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是
A.
B.
C.
D.
如图,在平面直角坐标系中,平行四边形OACB的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过(
)秒该直线可将□OABC的面积平分.?
A.
4
B.
5
C.
6
D.
7
如图,□ABCD中,点E、F分别在AD、AB上,依次连接EB、EC、FC、FD,图中阴影部分的面积分别为S1、S2、S3、S4,已知S1=2、S2=12、S3=3,则S4的值是(?
)
A.
4
B.
5
C.
6
D.
7
如图,AB=4,AC=2,以BC为边向上构造等边三角形BCD,连接AD并延长至点P,使AD=PD,则PB的最小值是( )
A.
B.
4-2
C.
4-
D.
4-4
二、填空题(本大题共8小题,共24.0分)
已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为________cm.
若?ABCD中,,则=_______
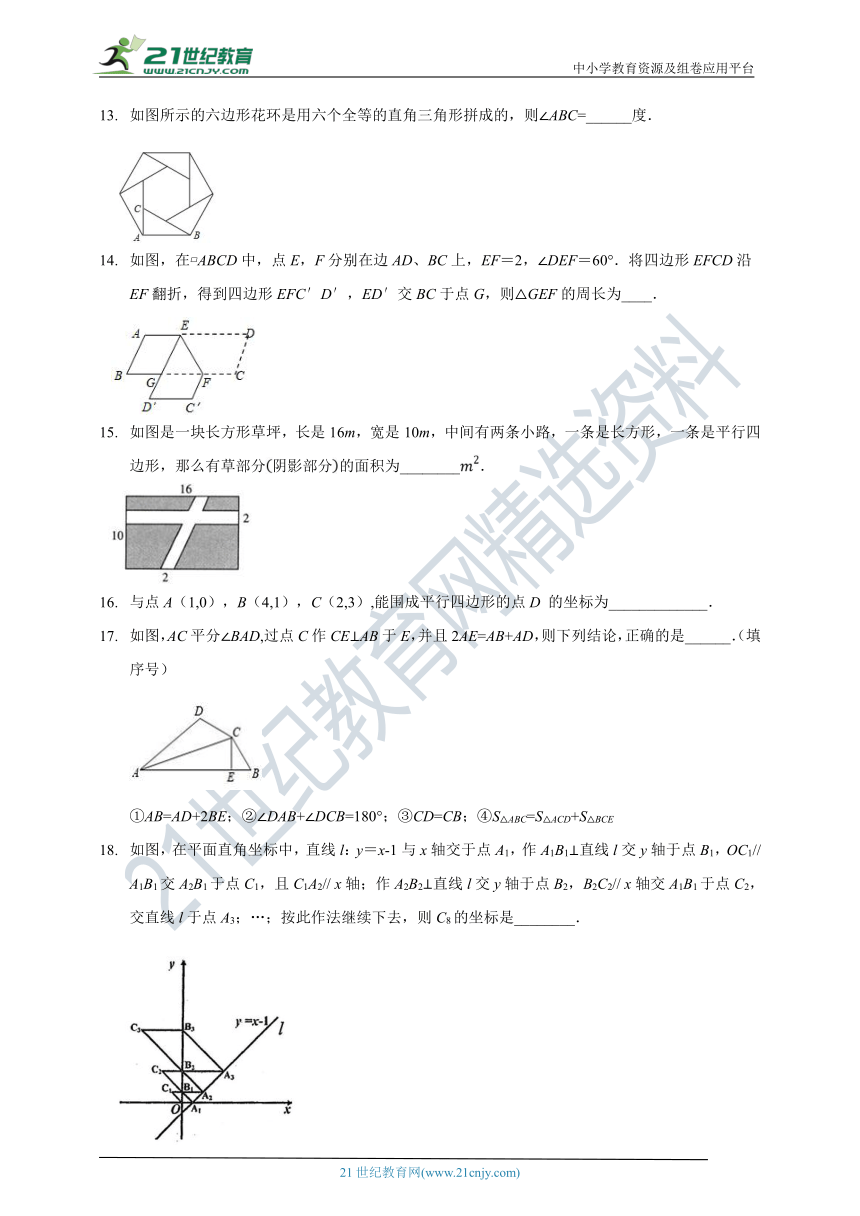
如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC=______度.
如图,在?ABCD中,点E,F分别在边AD、BC上,EF=2,∠DEF=60°.将四边形EFCD沿EF翻折,得到四边形EFC′D′,ED′交BC于点G,则△GEF的周长为____.
如图是一块长方形草坪,长是16m,宽是10m,中间有两条小路,一条是长方形,一条是平行四边形,那么有草部分阴影部分的面积为________.
与点A(1,0),B(4,1),C(2,3),能围成平行四边形的点D
的坐标为_____________.
如图,AC平分∠BAD,过点C作CE⊥AB于E,并且2AE=AB+AD,则下列结论,正确的是______.(填序号)
①AB=AD+2BE;②∠DAB+∠DCB=180°;③CD=CB;④S△ABC=S△ACD+S△BCE
如图,在平面直角坐标中,直线l:y=x-1与x轴交于点A1,作A1B1⊥直线l交y轴于点B1,OC1//
A1B1交A2B1于点C1,且C1A2//
x轴;作A2B2⊥直线l交y轴于点B2,B2C2//
x轴交A1B1于点C2,交直线l于点A3;…;按此作法继续下去,则C8的坐标是________.
三、解答题(本大题共6小题,共46.0分)
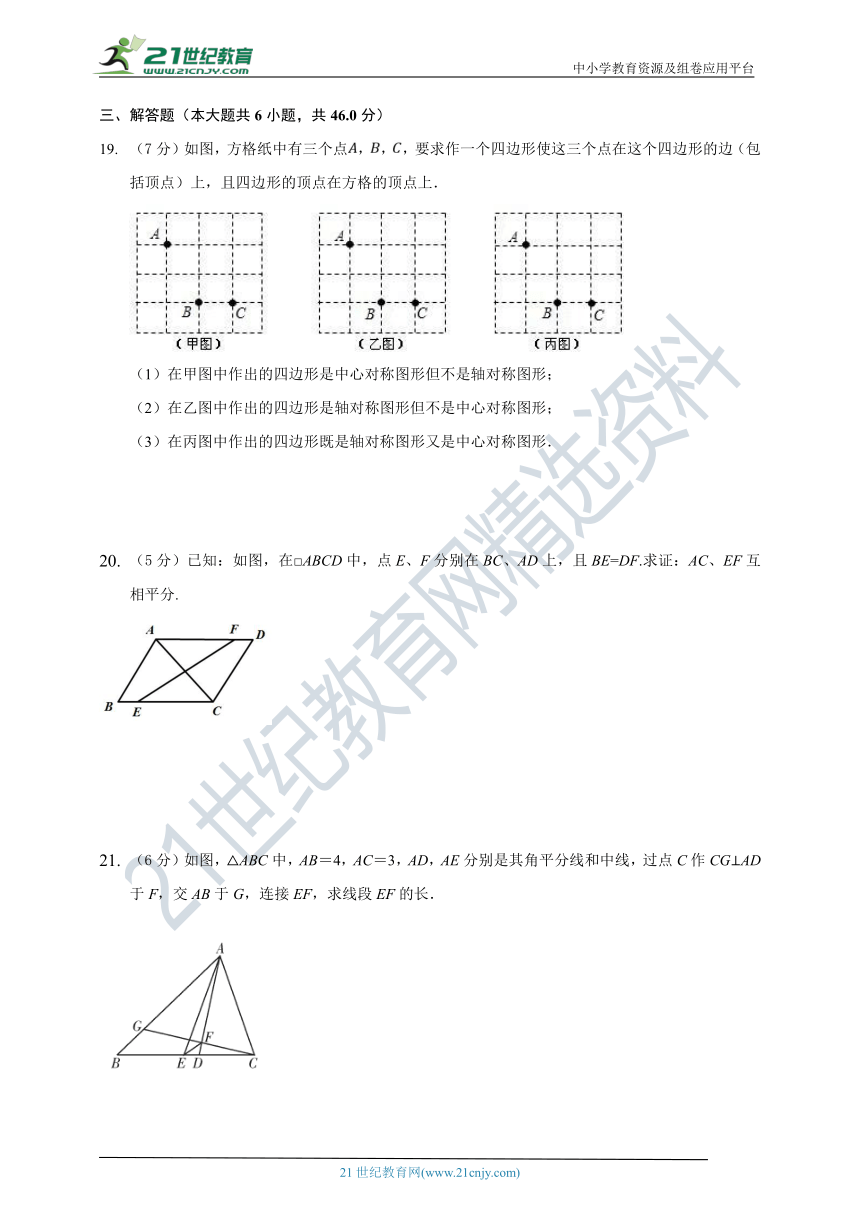
(7分)如图,方格纸中有三个点,,,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
(5分)已知:如图,在□ABCD中,点E、F分别在BC、AD上,且BE=DF.求证:AC、EF互相平分.
(6分)如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
(8分)如图,在四边形ABCD中,AC、BD相交于O,,O为BD的中心,过点C作交AD的延长线于点E.
?
求证:四边形ABCD为平行四边形.
若,,,连接EO,求的面积.
(10分)如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=,∠D=;
(1)如图①,>180°,试用,表示∠F;
(2)如图②,<180°,请在图中画出∠F,并试用,表示∠F;
(3)一定存在∠F吗?如有,求出∠F的值,如不一定,指出,满足什么条件时,不存在∠F.?
(10分)已知直线y=-
x+6与x轴,y轴分别相交于点A,B,直线y=﹣2x+6与x轴,y轴分别相交于点C,B,若已知x轴上有一点D(5,0),点M为直线AB上一点,点N为直线BC上一点,是否存在这样的点M、N,使得以点A、D、M、N为顶点的四边形是平行四边形?若存在,求出点M的坐标;若不存在,说明理由;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
备用图?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?备用图
答案和解析
1.【答案】A
【解析】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.不是轴对称图形,是中心对称图形,故本选项不合题意;
D.不是轴对称图形,也不是中心对称图形,故本选项不合题意.
2.【答案】D
【解析】解:∵AO=AC=4,
∴在△AOB中,AB-AO=6-4=2<BO<AB+AO=4+6=10,
即2<BO<10,
∴4<BD=2BO<20.
3.【答案】D
【解析】解:A.因为有两组对边分别平行的图形可能不是四边形,如正六边形,所以说法错误;B.平行四边形的对角线是不相等的,所以说法错误;C.平行四边形的对角相等,邻角互补,所以说法错误;D.平行四边形的对边平行且相等,说法正确;
4.【答案】B
【解析】解:∵多边形的每个内角都是108°,
∴每个外角是180°-108°=72°,
∴这个多边形的边数是360°÷72°=5,
∴这个多边形是五边形,
则此多边形的内角和为(5-2)×180°=540°.
5.【答案】D
【解析】解:反证法证明“四边形中至少有一个内角大于或等于90°”时,
假设每一个内角都小于90°,故选:D.
6.【答案】C
7.【答案】D
【解析】解:由平行四边形的判定方法可知:若是四边形的对角线互相平分,可证明这个四边形是平行四边形,①不能证明对角线互相平分,只有②③④可以.
8.【答案】C
【解析】解:如图
连接AC、BO,交于点D,
当y=2x+1经过D点时,该直线可将?OABC的面积平分;
四边形AOCB是平行四边形,
BD=OD,
B(6,2),点C(4,0),
D(3,1),
设直线y=2x+1平移后的直线为
y=kx+b,
平行于y=2x+1,
k=2,
过D(3,1),
y=2x-5,
直线y=2x+1要向下平移6个单位,
时间为6秒.
9.【答案】A
【解析】解:设平行四边形的面积为S,则S△CBE=S△CDF=S,
由图形可知,△CDF面积+△CBE面积+(S1+S4+S3)-S2=平行四边形ABCD的面积
∴S=S△CBE+S△CDF+2+S4+3-12,
即S=S+S+2+S4+3-12,
解得S4=7
10.【答案】D
【解析】解:如图,以AB为边构造等边三角形A′AB,连接A′P,取AB的中点M,连接DM,
在等边三角形A′AB和等边三角形BCD中,
AB=A′B,BC=BD,∠ABA′=∠CBD=60°,
∴∠ABC=60°-∠ADB,∠A′BD=60°-∠ABD,
∴∠ABC=∠A′BD,
在△ABC和△A′BD中,
,
∴△ABC≌△A′BD(SAS),
∴AC=A′D=2,
∵AD=PD,AM=BM,
∴DM是△ABP的中位线,
∴PB=2DM,
∴当DM最小时,PB有最小值,
∵△AA′B是等边三角形,M是AB中点,
∴当点A,D,M在同一条直线上时,DM有最小值,
此时,A′A=4,AM=2,A′M⊥AB,
∴A′M===2,
∴DM=A′M-A′D=2-2,
∴PB的最小值是4-4.
11.【答案】17
【解析】解:如图,???????
∵D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC=3.5(cm),同理,EF=AB=6(cm),DE=AC=7.5(cm),
∴△DEF的周长=3.5+6+7.5=17(cm)
12.【答案】125°
【解析】解:在□ABCD中,AD∥BC,∠A=∠C,
∴∠A+∠B=180°,
∵∠A-∠B=70°,
∴∠A=125°
13.【答案】30
【解析】解:正六边形的每个内角的度数为:=120°,
所以∠ABC=120°-90°=30°
14.【答案】6
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠AEG=∠EGF,
∵将四边形EFCD沿EF翻折,得到EFC′D′,
∴∠GEF=∠DEF=60°,
∴∠AEG=60°,∴∠EGF=60°,
∴△EGF是等边三角形,
∵EF=2,
∴△GEF的周长=6
15.【答案】112
【解析】本题主要考查求长方形的面积,解答此题的关键是利用“靠边站”原理,将小路靠边,即可求出有草部分的面积.由题意可知:求有草部分的面积,实际上就是求长为(16-2)米,宽为(10-2)米的长方形的面积,利用长方形的面积公式即可求解.
解:(16-2)×(10-2)=14×8=112(平方米)
16.【答案】(-1,2)或(5,4)或(3,-2)
【解析】解:如图
若AB为对角线,则组成的平行四边形D的坐标是(3,-2);
若AC为对角线,则组成的平行四边形D的坐标是(-1,2);
若BC为对角线,则组成的平行四边形D的坐标是(5,4),
综上可得点D的坐标是(-1,2)或(5,4)或(3,-2)
17.【答案】①②③
【解析】解:如图,过C作CF⊥AD于F,
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CF=CE,
∴Rt△ACF≌Rt△ACE(HL),
∴AF=AE,
∴AB+AD=(AE+BE)+(AF-DF)=2AE+BE-DF,
又∵AB+AD=2AE,
∴BE=DF,
∴AB-AD=(AE+BE)-(AF-DF)=BE+DF=2BE,
即AB=AD+2BE,故①正确;
∵BE=DF,∠CEB=∠F=90°,CF=CE,
∴△CDF≌△CBE(SAS),
∴∠B=∠CDF,CD=CB,故③正确;
又∵∠ADC+∠CDF=180°,
∴∠ADC+∠B=180°,
∴四边形ABCD中,∠DAB+∠BCD=360°-180°=180°,故②正确;
∵AB=AD+2BE,CE=CF,
由等式性质可得ABCE=ADCF+2BECE,
即=+,故错误;
故答案为①②③.
18.【答案】(-128,255)
【解析】解:∵y=x-1与x轴交于点A1,
∴A1点坐标(1,0),
∵A1B1⊥直线l,∴OA1B1为等腰直角三角形,∴B1坐标(0,1),
∵OC1∥A1B1,且C1A2∥x轴,∴四边形A1B1C1O是平行四边形,∴C1坐标(-1,1),
∵C1A2∥x轴,∴A2坐标(2,1),
∵A2B2⊥直线l,∴B1A2B2为等腰直角三角形,∴B2坐标(0,3),
∵B1C2∥A2B2,且C2A3∥x轴,∴四边形A2B2C2B1是平行四边形,∴C2坐标(-2,3),
∵C2A3∥x轴,∴A3坐标(4,3),
∵A3B3⊥直线l,∴B2A3B3为等腰直角三角形,∴B3坐标(0,8),
∵B2C3∥A3B3,且C3A4∥x轴,∴四边形A3B3C3B2是平行四边形,∴C3坐标(-4,7),
∵C1(-20,21-1),C2(-21,22-1),C3(-22,23-1),…,
∴Cn坐标(-2n-1,2n-1),
∴C8坐标(-27,28-1),即C8坐标(-128,255)
19.【答案】解:(1)甲图:平行四边形,
(2)乙图:等腰梯形,
(3)丙图:正方形.
20.【答案】证明:连接AE、CF,?
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵DF=BE,
∴AF=CE,
又∵AF∥CE,
∴四边形AECF为平行四边形,
∴AC、EF互相平分.
21.【答案】解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=3,GF=CF,
则BG=AB-AG=4-3=1.
又∵BE=CE,
∴EF是△BCG的中位线,∴EF=BG=.
【解析】本题考查了全等三角形的判定以及三角形的中位线定理,正确证明GF=CF是关键.首先证明△AGF≌△ACF,则AG=AC=3,GF=CF,证明EF是△BCG的中位线,利用三角形的中位线定理即可求解.
22.【答案】解:(1)证明:∵AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC,
∵O为BD的中点,
∴OB=OD,
在△OAB和△OCD中,
,
∴△OAB≌△OCD(AAS),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD为平行四边形;
(2)解:∵CE⊥AD,
∴∠CED=90°,
∵DE=CE,CD=,
∴CE==3,
∵∠EAC=30°,
∴AC=2CE=2×3=6,
由勾股定理得:AE=,
∴S△ACE=AE?CE=,
由(1)得四边形ABCD为平行四边形,
∴OA=OC,
∴S△AOE=S△ACE=.
【解析】(1)由AAS证得△OAB≌△OCD,得出AB=CD,即可得出结论;
(2)由等腰直角三角形的性质得出CE=3,由含30°角直角三角形的性质得出AC=2CE=6,由勾股定理得AE=,则S△ACE=AE?CE=,由(1)得四边形ABCD为平行四边形,得出OA=OC,则S△AOE=S△ACE,即可得出结果.
23.【答案】解:(1)∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠FBC+(180°-2∠DCF)=180°-2(∠DCF-∠FBC)=180°-2∠F,
∴360°-(α+β)=180°-2∠F,
2∠F=α+β-180°,
∴∠F=(α+β)-90°;
(2)如图②:
∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠GBC+(180°-2∠HCE)=180°+2(∠GBC-∠HCE)=180°+2∠F,
∴360°-(α+β)=180°+2∠F,
∴∠F=90°-(α+β);
(3)α+β=180°时,不存在∠F.
【解析】(1)先根据四边形内角和等于360°,得出∠ABC+∠DCB=360°-(α+β),根据内角与外角的关系和角平分线的定义得出∠ABC+(180°-∠DCE)=360°-(α+β)=2∠FBC+(180°-2∠DCF)=180°-2(∠DCF-∠FBC)=180°-2∠F,从而得出结论;
(2)先作出图形,根据四边形内角和等于360°,得出∠ABC+∠DCB=360°-(α+β),根据内角与外角的关系和角平分线的定义得出∠ABC+(180°-∠DCE)=360°-(α+β)=2∠GBC+(180°-2∠HCE)=180°+2(∠GBC-∠HCE)=180°+2∠F,从而得出结论;
(3)α,β满足α+β=180°时,∠ABC的角平分线及外角∠DCE的平分线平行,可知不存在∠F.
24.【答案】解:存在点M、N,使得以点A、D、M、N为顶点的四边形是平行四边形.
∵直线y=﹣x+6与x轴,y轴分别相交于点A,B,
则点A、B的坐标分别为:(8,0)、(0,6),
∴AD=3,
∵点M为直线AB上一点,点N为直线BC上一点,
∴设点M(m,-m+6),点N(n,-2n+6),
①当AD是平行四边形的边时,则MN=AD,且MN∥AD,
即:-m+6=-2n+6,
m-n=±3,
解得:m=±,
故点M(,)或(-,);
②当AD是平行四边形的对角线时,AD的中点坐标为(6.5,0),
∴m-6.5=6.5-n,-m+6-2n+6=0,
解得:m=,
故点M(,-);
综上,点M(,)或(-,)或((,-).
【解析】本题是一道一次函数综合题,考查的知识有平行四边形的性质等.根据已知条件求出点A、B的坐标,即可求出AD,根据点M为直线AB上一点,点N为直线BC上一点,设点M(m,-m+6),点N(n,-2n+6),分两种情况进行讨论:①当AD是平行四边形的边时;②当AD是平行四边形的对角线时,分别求解即可.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
八年级下册数学
平行四边形
单元测试卷
(满分100分)
题号
一
二
三
总分
得分
一、选择题(本大题共10小题,共30.0分)
下列图标中,既是轴对称图形,又是中心对称图形的是(
)
A.
B.
C.
D.
如图,?ABCD中,对角线AC和BD相交于点O,若AC=8,AB=6,BD=m,那么m的取范围是(?
?
)
A.
2<m<10
B.
2<m<14
C.
6<m<8
D.
4<m<20
下列说法正确的是(
)
A.
有两组对边分别平行的图形是平行四边形
B.
平行四边形的对角线相等
C.
平行四边形的对角互补,邻角相等
D.
平行四边形的对边平行且相等
若一个多边形的每个内角都是108°,则这个多边形的内角和为(
)
A.
360°
B.
540°
C.
720°
D.
900°
用反证法证明“四边形中至少有一个内角大于或等于90°”时,应先假设( )
A.
有一个内角小于90°
B.
每一个内角都大于90°
C.
有一个内角小于或等于90°
D.
每一个内角都小于90°
如图,将?ABCD沿对角线AC折叠,使点B落在B'处.若1=2=,则B为(?
?
)
A.
B.
C.
D.
如图,点E,F是平行四边形ABCD对角线上两点,在条件;;;中,添加一个条件,使四边形DEBF是平行四边形,可添加的条件是
A.
B.
C.
D.
如图,在平面直角坐标系中,平行四边形OACB的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+1以每秒1个单位的速度向下平移,经过(
)秒该直线可将□OABC的面积平分.?
A.
4
B.
5
C.
6
D.
7
如图,□ABCD中,点E、F分别在AD、AB上,依次连接EB、EC、FC、FD,图中阴影部分的面积分别为S1、S2、S3、S4,已知S1=2、S2=12、S3=3,则S4的值是(?
)
A.
4
B.
5
C.
6
D.
7
如图,AB=4,AC=2,以BC为边向上构造等边三角形BCD,连接AD并延长至点P,使AD=PD,则PB的最小值是( )
A.
B.
4-2
C.
4-
D.
4-4
二、填空题(本大题共8小题,共24.0分)
已知三角形三条边的长分别是7cm,12cm,15cm,则连接三边中点所构成三角形的周长为________cm.
若?ABCD中,,则=_______
如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC=______度.
如图,在?ABCD中,点E,F分别在边AD、BC上,EF=2,∠DEF=60°.将四边形EFCD沿EF翻折,得到四边形EFC′D′,ED′交BC于点G,则△GEF的周长为____.
如图是一块长方形草坪,长是16m,宽是10m,中间有两条小路,一条是长方形,一条是平行四边形,那么有草部分阴影部分的面积为________.
与点A(1,0),B(4,1),C(2,3),能围成平行四边形的点D
的坐标为_____________.
如图,AC平分∠BAD,过点C作CE⊥AB于E,并且2AE=AB+AD,则下列结论,正确的是______.(填序号)
①AB=AD+2BE;②∠DAB+∠DCB=180°;③CD=CB;④S△ABC=S△ACD+S△BCE
如图,在平面直角坐标中,直线l:y=x-1与x轴交于点A1,作A1B1⊥直线l交y轴于点B1,OC1//
A1B1交A2B1于点C1,且C1A2//
x轴;作A2B2⊥直线l交y轴于点B2,B2C2//
x轴交A1B1于点C2,交直线l于点A3;…;按此作法继续下去,则C8的坐标是________.
三、解答题(本大题共6小题,共46.0分)
(7分)如图,方格纸中有三个点,,,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在甲图中作出的四边形是中心对称图形但不是轴对称图形;
(2)在乙图中作出的四边形是轴对称图形但不是中心对称图形;
(3)在丙图中作出的四边形既是轴对称图形又是中心对称图形.
(5分)已知:如图,在□ABCD中,点E、F分别在BC、AD上,且BE=DF.求证:AC、EF互相平分.
(6分)如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
(8分)如图,在四边形ABCD中,AC、BD相交于O,,O为BD的中心,过点C作交AD的延长线于点E.
?
求证:四边形ABCD为平行四边形.
若,,,连接EO,求的面积.
(10分)如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=,∠D=;
(1)如图①,>180°,试用,表示∠F;
(2)如图②,<180°,请在图中画出∠F,并试用,表示∠F;
(3)一定存在∠F吗?如有,求出∠F的值,如不一定,指出,满足什么条件时,不存在∠F.?
(10分)已知直线y=-
x+6与x轴,y轴分别相交于点A,B,直线y=﹣2x+6与x轴,y轴分别相交于点C,B,若已知x轴上有一点D(5,0),点M为直线AB上一点,点N为直线BC上一点,是否存在这样的点M、N,使得以点A、D、M、N为顶点的四边形是平行四边形?若存在,求出点M的坐标;若不存在,说明理由;
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
备用图?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?备用图
答案和解析
1.【答案】A
【解析】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不合题意;
C.不是轴对称图形,是中心对称图形,故本选项不合题意;
D.不是轴对称图形,也不是中心对称图形,故本选项不合题意.
2.【答案】D
【解析】解:∵AO=AC=4,
∴在△AOB中,AB-AO=6-4=2<BO<AB+AO=4+6=10,
即2<BO<10,
∴4<BD=2BO<20.
3.【答案】D
【解析】解:A.因为有两组对边分别平行的图形可能不是四边形,如正六边形,所以说法错误;B.平行四边形的对角线是不相等的,所以说法错误;C.平行四边形的对角相等,邻角互补,所以说法错误;D.平行四边形的对边平行且相等,说法正确;
4.【答案】B
【解析】解:∵多边形的每个内角都是108°,
∴每个外角是180°-108°=72°,
∴这个多边形的边数是360°÷72°=5,
∴这个多边形是五边形,
则此多边形的内角和为(5-2)×180°=540°.
5.【答案】D
【解析】解:反证法证明“四边形中至少有一个内角大于或等于90°”时,
假设每一个内角都小于90°,故选:D.
6.【答案】C
7.【答案】D
【解析】解:由平行四边形的判定方法可知:若是四边形的对角线互相平分,可证明这个四边形是平行四边形,①不能证明对角线互相平分,只有②③④可以.
8.【答案】C
【解析】解:如图
连接AC、BO,交于点D,
当y=2x+1经过D点时,该直线可将?OABC的面积平分;
四边形AOCB是平行四边形,
BD=OD,
B(6,2),点C(4,0),
D(3,1),
设直线y=2x+1平移后的直线为
y=kx+b,
平行于y=2x+1,
k=2,
过D(3,1),
y=2x-5,
直线y=2x+1要向下平移6个单位,
时间为6秒.
9.【答案】A
【解析】解:设平行四边形的面积为S,则S△CBE=S△CDF=S,
由图形可知,△CDF面积+△CBE面积+(S1+S4+S3)-S2=平行四边形ABCD的面积
∴S=S△CBE+S△CDF+2+S4+3-12,
即S=S+S+2+S4+3-12,
解得S4=7
10.【答案】D
【解析】解:如图,以AB为边构造等边三角形A′AB,连接A′P,取AB的中点M,连接DM,
在等边三角形A′AB和等边三角形BCD中,
AB=A′B,BC=BD,∠ABA′=∠CBD=60°,
∴∠ABC=60°-∠ADB,∠A′BD=60°-∠ABD,
∴∠ABC=∠A′BD,
在△ABC和△A′BD中,
,
∴△ABC≌△A′BD(SAS),
∴AC=A′D=2,
∵AD=PD,AM=BM,
∴DM是△ABP的中位线,
∴PB=2DM,
∴当DM最小时,PB有最小值,
∵△AA′B是等边三角形,M是AB中点,
∴当点A,D,M在同一条直线上时,DM有最小值,
此时,A′A=4,AM=2,A′M⊥AB,
∴A′M===2,
∴DM=A′M-A′D=2-2,
∴PB的最小值是4-4.
11.【答案】17
【解析】解:如图,???????
∵D、F分别为AB、AC的中点,
∴DF是△ABC的中位线,
∴DF=BC=3.5(cm),同理,EF=AB=6(cm),DE=AC=7.5(cm),
∴△DEF的周长=3.5+6+7.5=17(cm)
12.【答案】125°
【解析】解:在□ABCD中,AD∥BC,∠A=∠C,
∴∠A+∠B=180°,
∵∠A-∠B=70°,
∴∠A=125°
13.【答案】30
【解析】解:正六边形的每个内角的度数为:=120°,
所以∠ABC=120°-90°=30°
14.【答案】6
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠AEG=∠EGF,
∵将四边形EFCD沿EF翻折,得到EFC′D′,
∴∠GEF=∠DEF=60°,
∴∠AEG=60°,∴∠EGF=60°,
∴△EGF是等边三角形,
∵EF=2,
∴△GEF的周长=6
15.【答案】112
【解析】本题主要考查求长方形的面积,解答此题的关键是利用“靠边站”原理,将小路靠边,即可求出有草部分的面积.由题意可知:求有草部分的面积,实际上就是求长为(16-2)米,宽为(10-2)米的长方形的面积,利用长方形的面积公式即可求解.
解:(16-2)×(10-2)=14×8=112(平方米)
16.【答案】(-1,2)或(5,4)或(3,-2)
【解析】解:如图
若AB为对角线,则组成的平行四边形D的坐标是(3,-2);
若AC为对角线,则组成的平行四边形D的坐标是(-1,2);
若BC为对角线,则组成的平行四边形D的坐标是(5,4),
综上可得点D的坐标是(-1,2)或(5,4)或(3,-2)
17.【答案】①②③
【解析】解:如图,过C作CF⊥AD于F,
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CF=CE,
∴Rt△ACF≌Rt△ACE(HL),
∴AF=AE,
∴AB+AD=(AE+BE)+(AF-DF)=2AE+BE-DF,
又∵AB+AD=2AE,
∴BE=DF,
∴AB-AD=(AE+BE)-(AF-DF)=BE+DF=2BE,
即AB=AD+2BE,故①正确;
∵BE=DF,∠CEB=∠F=90°,CF=CE,
∴△CDF≌△CBE(SAS),
∴∠B=∠CDF,CD=CB,故③正确;
又∵∠ADC+∠CDF=180°,
∴∠ADC+∠B=180°,
∴四边形ABCD中,∠DAB+∠BCD=360°-180°=180°,故②正确;
∵AB=AD+2BE,CE=CF,
由等式性质可得ABCE=ADCF+2BECE,
即=+,故错误;
故答案为①②③.
18.【答案】(-128,255)
【解析】解:∵y=x-1与x轴交于点A1,
∴A1点坐标(1,0),
∵A1B1⊥直线l,∴OA1B1为等腰直角三角形,∴B1坐标(0,1),
∵OC1∥A1B1,且C1A2∥x轴,∴四边形A1B1C1O是平行四边形,∴C1坐标(-1,1),
∵C1A2∥x轴,∴A2坐标(2,1),
∵A2B2⊥直线l,∴B1A2B2为等腰直角三角形,∴B2坐标(0,3),
∵B1C2∥A2B2,且C2A3∥x轴,∴四边形A2B2C2B1是平行四边形,∴C2坐标(-2,3),
∵C2A3∥x轴,∴A3坐标(4,3),
∵A3B3⊥直线l,∴B2A3B3为等腰直角三角形,∴B3坐标(0,8),
∵B2C3∥A3B3,且C3A4∥x轴,∴四边形A3B3C3B2是平行四边形,∴C3坐标(-4,7),
∵C1(-20,21-1),C2(-21,22-1),C3(-22,23-1),…,
∴Cn坐标(-2n-1,2n-1),
∴C8坐标(-27,28-1),即C8坐标(-128,255)
19.【答案】解:(1)甲图:平行四边形,
(2)乙图:等腰梯形,
(3)丙图:正方形.
20.【答案】证明:连接AE、CF,?
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵DF=BE,
∴AF=CE,
又∵AF∥CE,
∴四边形AECF为平行四边形,
∴AC、EF互相平分.
21.【答案】解:在△AGF和△ACF中,
,
∴△AGF≌△ACF(ASA),
∴AG=AC=3,GF=CF,
则BG=AB-AG=4-3=1.
又∵BE=CE,
∴EF是△BCG的中位线,∴EF=BG=.
【解析】本题考查了全等三角形的判定以及三角形的中位线定理,正确证明GF=CF是关键.首先证明△AGF≌△ACF,则AG=AC=3,GF=CF,证明EF是△BCG的中位线,利用三角形的中位线定理即可求解.
22.【答案】解:(1)证明:∵AB∥CD,
∴∠OAB=∠OCD,∠OBA=∠ODC,
∵O为BD的中点,
∴OB=OD,
在△OAB和△OCD中,
,
∴△OAB≌△OCD(AAS),
∴AB=CD,
又∵AB∥CD,
∴四边形ABCD为平行四边形;
(2)解:∵CE⊥AD,
∴∠CED=90°,
∵DE=CE,CD=,
∴CE==3,
∵∠EAC=30°,
∴AC=2CE=2×3=6,
由勾股定理得:AE=,
∴S△ACE=AE?CE=,
由(1)得四边形ABCD为平行四边形,
∴OA=OC,
∴S△AOE=S△ACE=.
【解析】(1)由AAS证得△OAB≌△OCD,得出AB=CD,即可得出结论;
(2)由等腰直角三角形的性质得出CE=3,由含30°角直角三角形的性质得出AC=2CE=6,由勾股定理得AE=,则S△ACE=AE?CE=,由(1)得四边形ABCD为平行四边形,得出OA=OC,则S△AOE=S△ACE,即可得出结果.
23.【答案】解:(1)∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠FBC+(180°-2∠DCF)=180°-2(∠DCF-∠FBC)=180°-2∠F,
∴360°-(α+β)=180°-2∠F,
2∠F=α+β-180°,
∴∠F=(α+β)-90°;
(2)如图②:
∵∠ABC+∠DCB=360°-(α+β),
∴∠ABC+(180°-∠DCE)=360°-(α+β)=2∠GBC+(180°-2∠HCE)=180°+2(∠GBC-∠HCE)=180°+2∠F,
∴360°-(α+β)=180°+2∠F,
∴∠F=90°-(α+β);
(3)α+β=180°时,不存在∠F.
【解析】(1)先根据四边形内角和等于360°,得出∠ABC+∠DCB=360°-(α+β),根据内角与外角的关系和角平分线的定义得出∠ABC+(180°-∠DCE)=360°-(α+β)=2∠FBC+(180°-2∠DCF)=180°-2(∠DCF-∠FBC)=180°-2∠F,从而得出结论;
(2)先作出图形,根据四边形内角和等于360°,得出∠ABC+∠DCB=360°-(α+β),根据内角与外角的关系和角平分线的定义得出∠ABC+(180°-∠DCE)=360°-(α+β)=2∠GBC+(180°-2∠HCE)=180°+2(∠GBC-∠HCE)=180°+2∠F,从而得出结论;
(3)α,β满足α+β=180°时,∠ABC的角平分线及外角∠DCE的平分线平行,可知不存在∠F.
24.【答案】解:存在点M、N,使得以点A、D、M、N为顶点的四边形是平行四边形.
∵直线y=﹣x+6与x轴,y轴分别相交于点A,B,
则点A、B的坐标分别为:(8,0)、(0,6),
∴AD=3,
∵点M为直线AB上一点,点N为直线BC上一点,
∴设点M(m,-m+6),点N(n,-2n+6),
①当AD是平行四边形的边时,则MN=AD,且MN∥AD,
即:-m+6=-2n+6,
m-n=±3,
解得:m=±,
故点M(,)或(-,);
②当AD是平行四边形的对角线时,AD的中点坐标为(6.5,0),
∴m-6.5=6.5-n,-m+6-2n+6=0,
解得:m=,
故点M(,-);
综上,点M(,)或(-,)或((,-).
【解析】本题是一道一次函数综合题,考查的知识有平行四边形的性质等.根据已知条件求出点A、B的坐标,即可求出AD,根据点M为直线AB上一点,点N为直线BC上一点,设点M(m,-m+6),点N(n,-2n+6),分两种情况进行讨论:①当AD是平行四边形的边时;②当AD是平行四边形的对角线时,分别求解即可.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
