直线圆的位置关系2 PPT课件 九年级数学 初三课件
文档属性
| 名称 | 直线圆的位置关系2 PPT课件 九年级数学 初三课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 590.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-31 00:00:00 | ||
图片预览

文档简介
(共12张PPT)
今天继续讲直线圆的位置关系
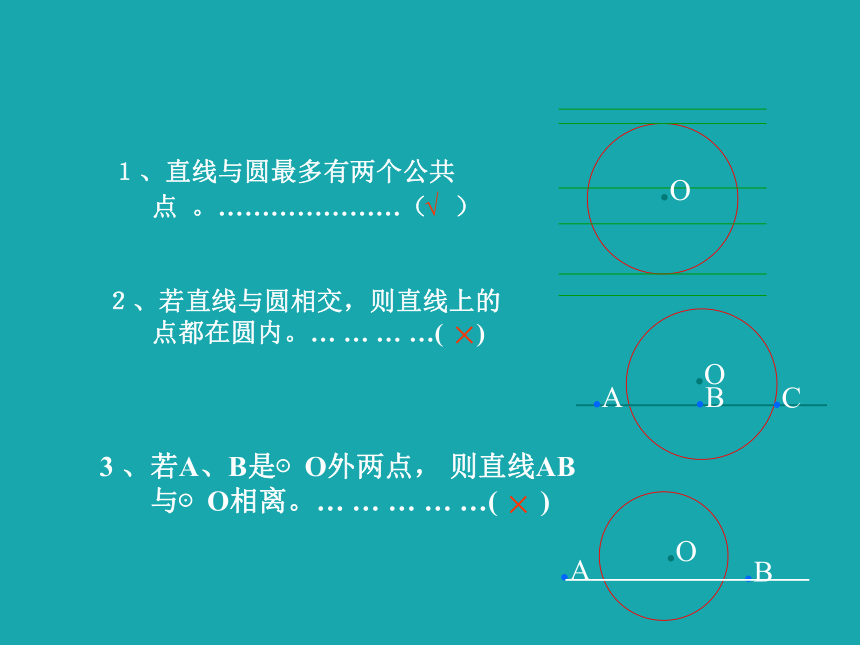
1、直线与圆最多有两个公共
点 。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。… … … …( )
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
√
×
.A
.B
.C
.O
.O
×
.A
.B
.O
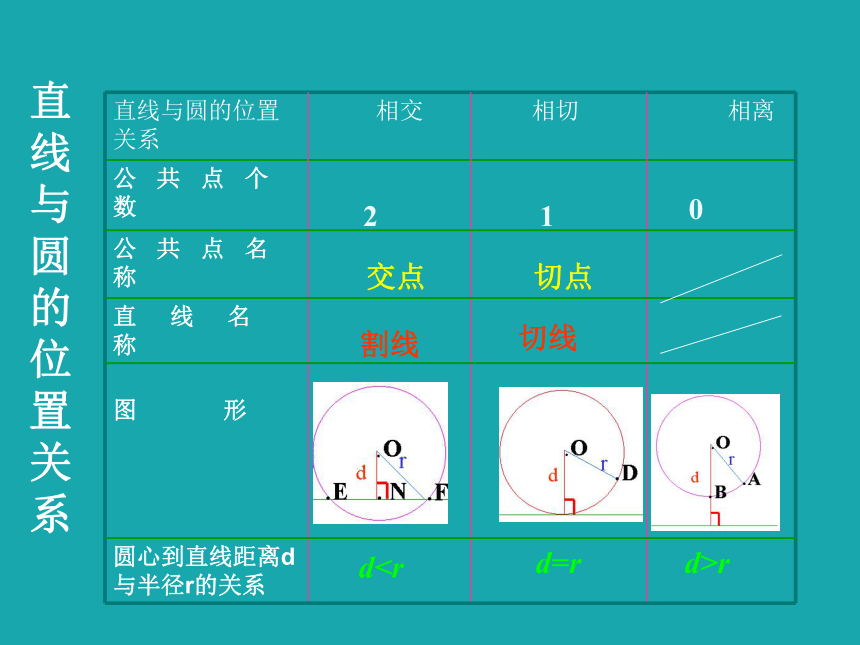
直线与圆的位置关系
直线与圆的位置关系 相交 相切 相离
公 共 点 个 数
公 共 点 名 称
直 线 名 称
图 形
圆心到直线距离d与半径r的关系
dd=r
d>r
2
交点
割线
1
切点
切线
0
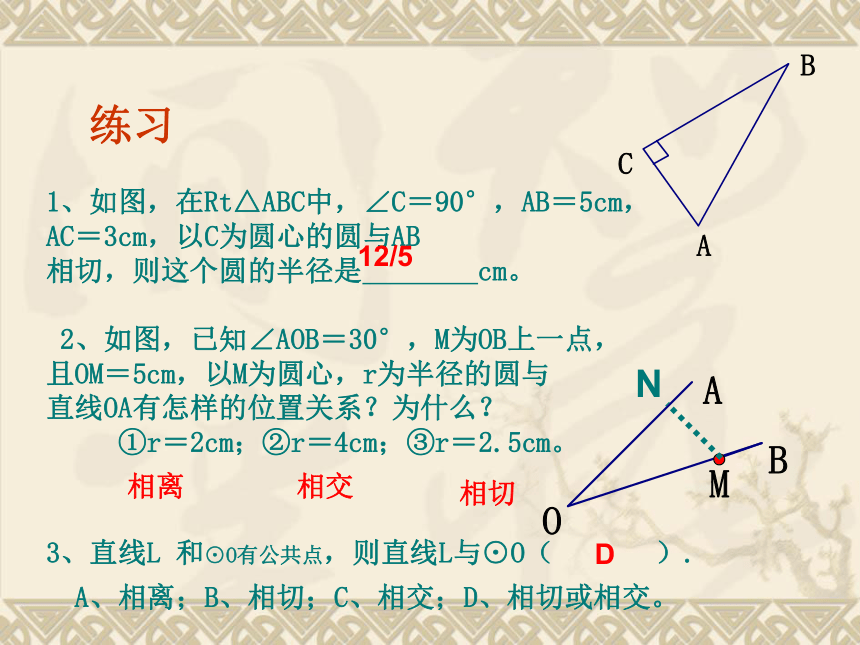
练习
1、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
2、如图,已知∠AOB=30°,M为OB上一点,
且OM=5cm,以M为圆心,r为半径的圆与
直线OA有怎样的位置关系?为什么?
①r=2cm;②r=4cm;③r=2.5cm。
3、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。
12/5
相离
相交
相切
D
N
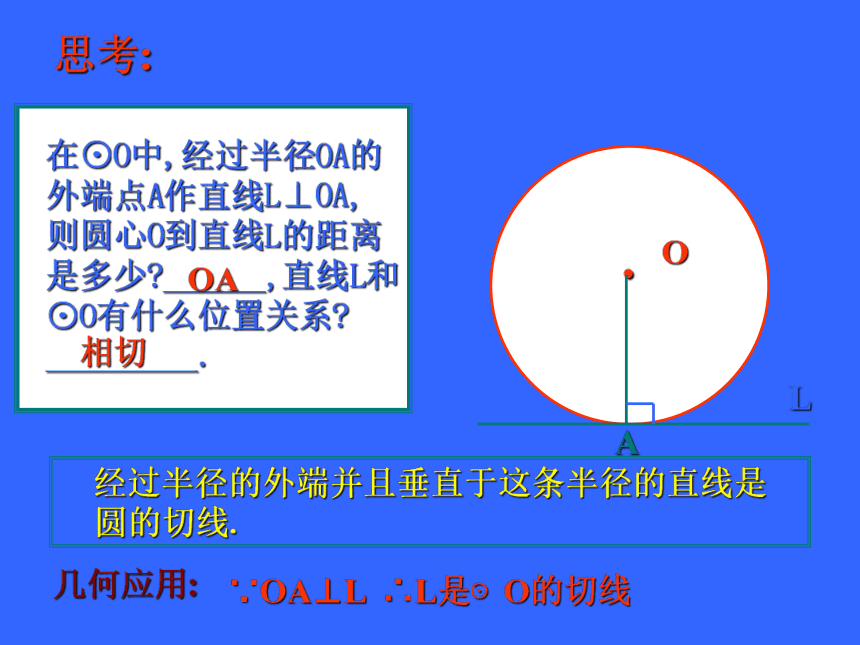
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少 ______,直线L和
⊙O有什么位置关系
_________.
思考:
.
O
A
OA
相切
L
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
几何应用:
∵OA⊥L ∴L是⊙O的切线
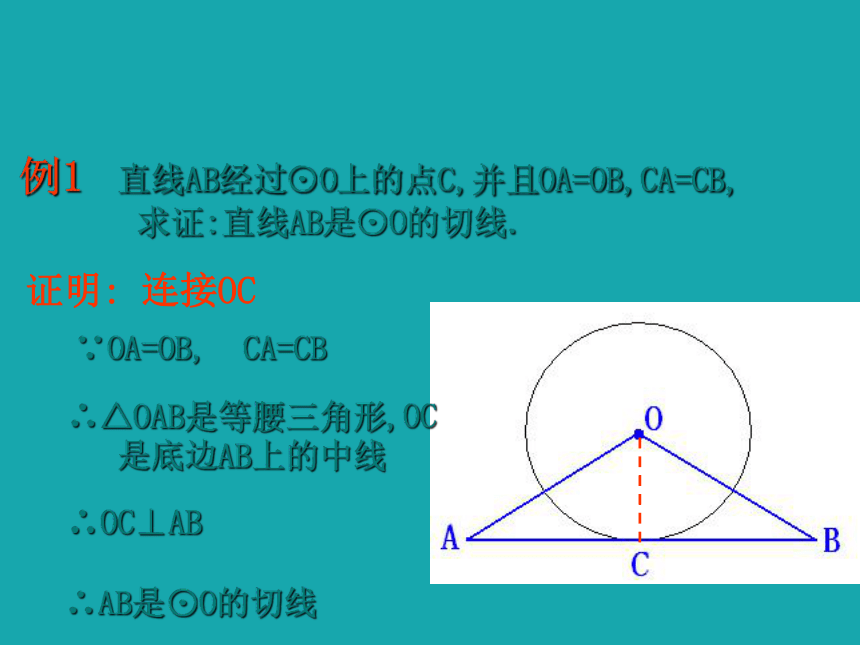
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB
∴AB是⊙O的切线
.
O
A
L
将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
A
l
O
圆O与直线L相切,则过点A的半径OA 与切线L有
怎样的位置关系?
垂直
反证法:假设直线圆O相切OA与直线L不垂直
T
拓展应用:
1.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.
F
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC的延长线于点D,试判断△AED的
形状,并说明理由.
希望同学们认真学习老师期盼你们快快进步!!
今天继续讲直线圆的位置关系
1、直线与圆最多有两个公共
点 。…………………( )
2、若直线与圆相交,则直线上的
点都在圆内。… … … …( )
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
√
×
.A
.B
.C
.O
.O
×
.A
.B
.O
直线与圆的位置关系
直线与圆的位置关系 相交 相切 相离
公 共 点 个 数
公 共 点 名 称
直 线 名 称
图 形
圆心到直线距离d与半径r的关系
d
d>r
2
交点
割线
1
切点
切线
0
练习
1、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
2、如图,已知∠AOB=30°,M为OB上一点,
且OM=5cm,以M为圆心,r为半径的圆与
直线OA有怎样的位置关系?为什么?
①r=2cm;②r=4cm;③r=2.5cm。
3、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。
12/5
相离
相交
相切
D
N
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少 ______,直线L和
⊙O有什么位置关系
_________.
思考:
.
O
A
OA
相切
L
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
几何应用:
∵OA⊥L ∴L是⊙O的切线
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB
∴AB是⊙O的切线
.
O
A
L
将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
A
l
O
圆O与直线L相切,则过点A的半径OA 与切线L有
怎样的位置关系?
垂直
反证法:假设直线圆O相切OA与直线L不垂直
T
拓展应用:
1.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.
F
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC的延长线于点D,试判断△AED的
形状,并说明理由.
希望同学们认真学习老师期盼你们快快进步!!
