3.1直线圆的位置关系
图片预览




文档简介
(共24张PPT)
一、复习提问
1、点和圆的位置关系有几种?
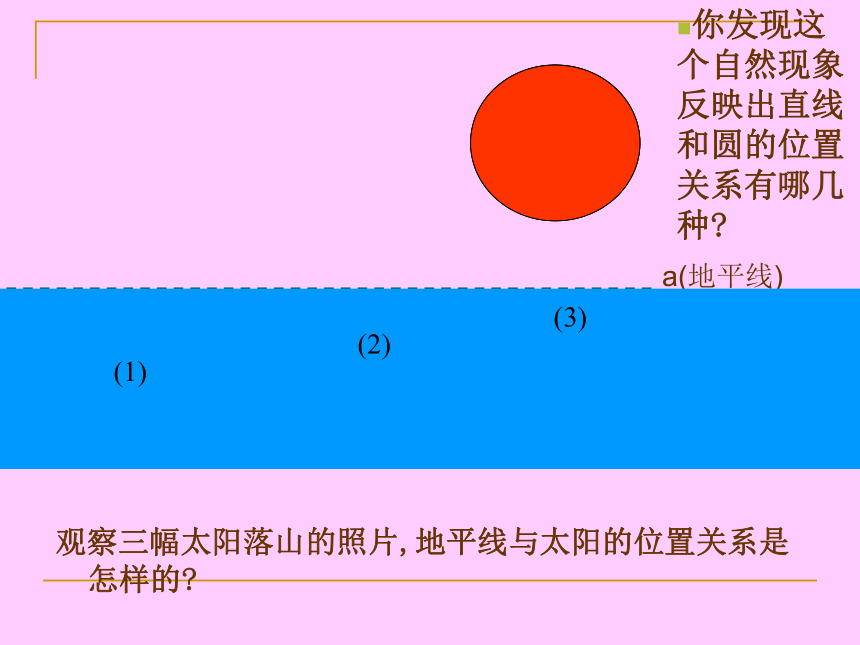
2、“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
(1)d(2)d=r 点在圆上
(3)d>r 点 在圆外
观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
a(地平线)
你发现这个自然现象反映出直线和圆的位置关系有哪几种
(1)
(3)
(2)
(2)如图,在纸上画一条直线 L,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线L的公共点的个数吗?
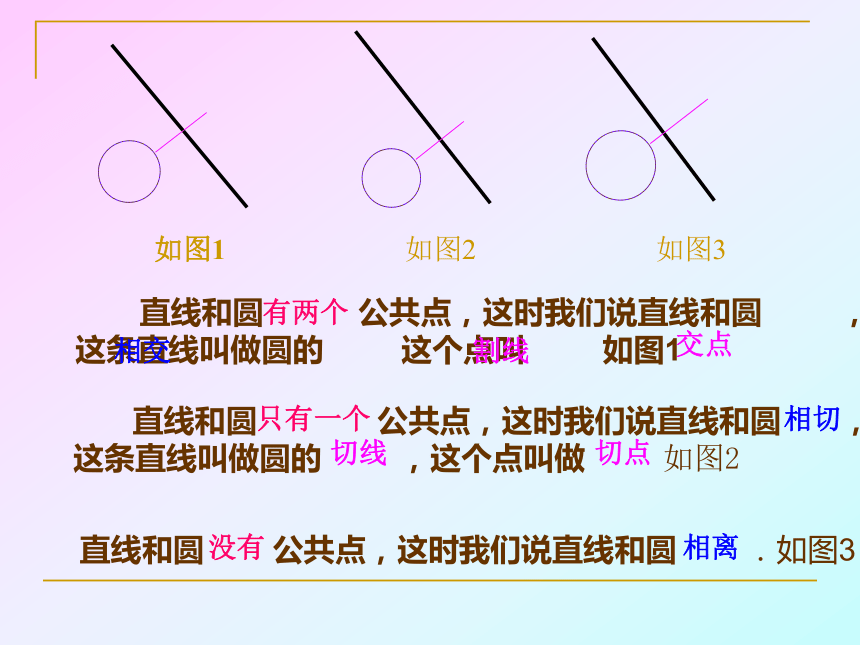
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 这个点叫 如图1
直线和圆 公共点,这时我们说直线和圆 .如图3
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 ,这个点叫做 如图2
如图1
如图2
如图3
有两个
相交
割线
只有一个
相切
切线
切点
没有
相离
交点
O
l
(1)直线和圆有两个公共点时,叫做直线和圆相交;这时直线叫做圆的割线.
O
l
(2)直线和圆有唯一公共点时,叫做直线和圆相切;这时直线叫做圆的切线. 唯一的公共点叫做切点.
O
l
(3)直线和圆没有公共点时,叫做直线和圆相离.
直线和圆的位置关系
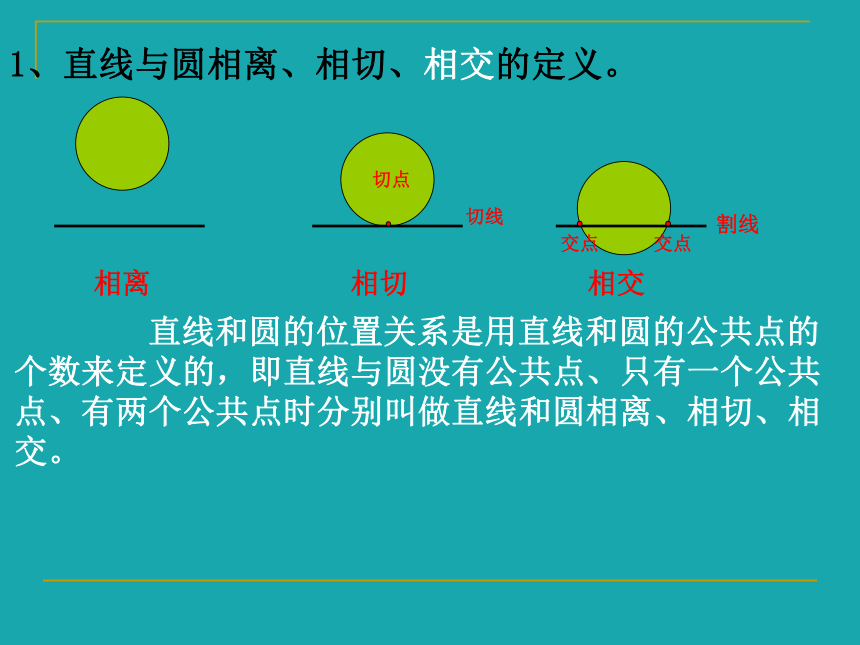
1、直线与圆相离、相切、相交的定义。
直线和圆的位置关系是用直线和圆的公共点的个数来定义的,即直线与圆没有公共点、只有一个公共点、有两个公共点时分别叫做直线和圆相离、相切、相交。
相离
相交
相切
切点
切线
割线
交点
交点
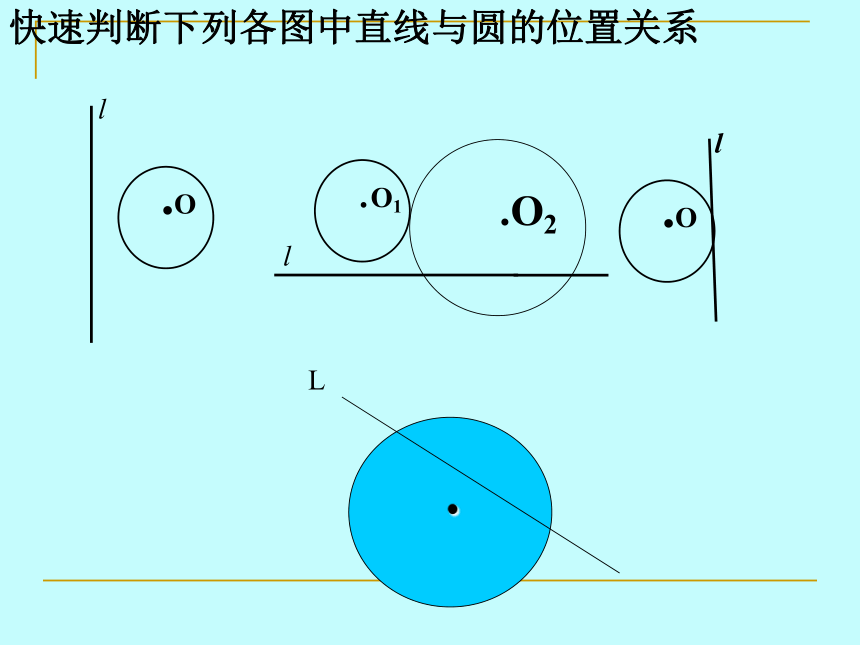
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
L
.
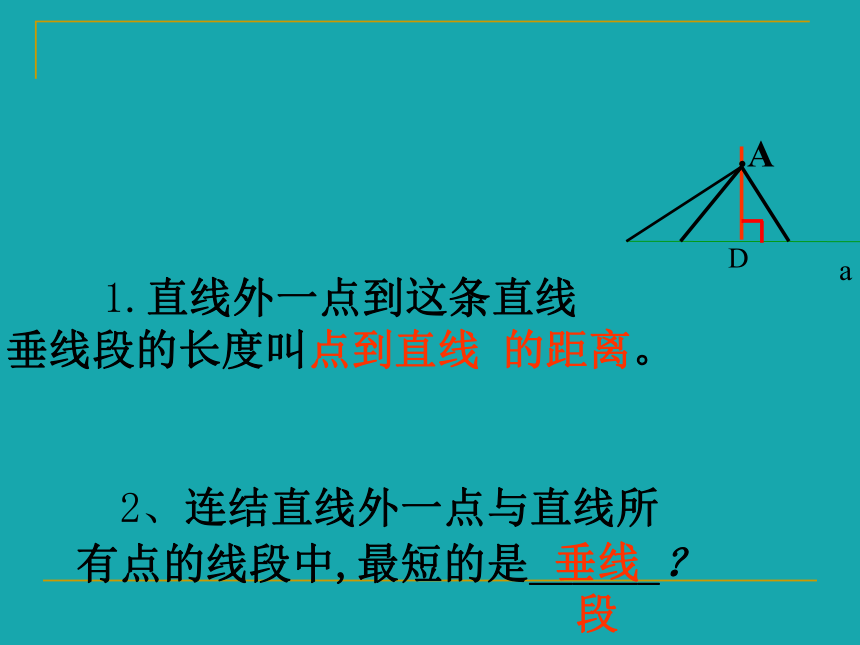
2、连结直线外一点与直线所
有点的线段中,最短的是______?
1.直线外一点到这条直线
垂线段的长度叫点到直线 的距离。
垂线段
a
.A
D
(2)直线l 和⊙O相切
2、用圆心到直线的距离和圆半径的数量关系,来揭示圆和直线的位置关系。
(1)直线l 和⊙O相离
(3)直线l 和⊙O相交
d>r
d=r
dd
o
r
l
d
o
r
l
o
d
r
l
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
O
l
O
l
O
l
r
d
┐
┐
d
┐
d
直线与圆的位置关系判定方法:
无
切线
割线
直线名称
无
切点
交点
公共点名称
d > r
d = r
d < r
圆心到直线距离
d 与半径 r 关系
0
1
2
公共点个数
相离
相切
相交
直线和圆的位置关系
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
三、练习与例题
0cm≤
2
1
0
3.直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相 交
相 切
相 离
1.根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
·
A
O
例
在 Rt△ABC 中,∠C = 90°,AC = 3 cm , BC = 4 cm , 以 C 为圆心,r 为半径的圆与 AB 有怎样的关系?为什么?(1)r = 2 cm ; (2) r = 2.4 cm ; (3) r = 3 cm .
A
C
B
D
解:
过 C 作 CD⊥AB 于 D,在 Rt △ABC 中,
根据三角形面积公式有
CD · AB = AC · BC
即圆心 C 到 AB 的距离 d = 2.4 cm.
(1) 当 r = 2 cm 时,
有 d > r ,因此⊙C 和 AB 相离.
(2) 当 r = 2.4 cm 时,
有 d = r ,因此⊙C 和 AB 相切.
(3) 当 r = 3 cm 时,
有 d < r ,因此⊙C 和 AB 相交.
练习(B组)
1、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
2、如图,已知∠AOB=30°,M为OB上一点,
且OM=5cm,以M为圆心,r为半径的圆与
直线OA有怎样的位置关系?为什么?
①r=2cm;②r=4cm;③r=2.5cm。
3、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。
12/5
相离
相交
相切
D
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少 ______,直线L和
⊙O有什么位置关系
_________.
思考:
.
O
A
OA
相切
L
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
几何应用:
∵OA⊥L ∴L是⊙O的切线
A
B
l
O
圆O与直线l相切,则过点A的直径A B与切线l有
怎样的位置关系?
垂直
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB
∴AB是⊙O的切线
.
O
A
L
将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
拓展应用:
1.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.
F
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC的延长线于点D,试判断△AED的
形状,并说明理由.
一、复习提问
1、点和圆的位置关系有几种?
2、“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?
(1)d
(3)d>r 点 在圆外
观察三幅太阳落山的照片,地平线与太阳的位置关系是怎样的
a(地平线)
你发现这个自然现象反映出直线和圆的位置关系有哪几种
(1)
(3)
(2)
(2)如图,在纸上画一条直线 L,把钥匙环看作一个圆,在纸上移动钥匙环,你能发现在钥匙环移动的过程中,它与直线L的公共点的个数吗?
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 这个点叫 如图1
直线和圆 公共点,这时我们说直线和圆 .如图3
直线和圆 公共点,这时我们说直线和圆 ,这条直线叫做圆的 ,这个点叫做 如图2
如图1
如图2
如图3
有两个
相交
割线
只有一个
相切
切线
切点
没有
相离
交点
O
l
(1)直线和圆有两个公共点时,叫做直线和圆相交;这时直线叫做圆的割线.
O
l
(2)直线和圆有唯一公共点时,叫做直线和圆相切;这时直线叫做圆的切线. 唯一的公共点叫做切点.
O
l
(3)直线和圆没有公共点时,叫做直线和圆相离.
直线和圆的位置关系
1、直线与圆相离、相切、相交的定义。
直线和圆的位置关系是用直线和圆的公共点的个数来定义的,即直线与圆没有公共点、只有一个公共点、有两个公共点时分别叫做直线和圆相离、相切、相交。
相离
相交
相切
切点
切线
割线
交点
交点
快速判断下列各图中直线与圆的位置关系
.O
l
.O1
.O
l
.O2
l
L
.
2、连结直线外一点与直线所
有点的线段中,最短的是______?
1.直线外一点到这条直线
垂线段的长度叫点到直线 的距离。
垂线段
a
.A
D
(2)直线l 和⊙O相切
2、用圆心到直线的距离和圆半径的数量关系,来揭示圆和直线的位置关系。
(1)直线l 和⊙O相离
(3)直线l 和⊙O相交
d>r
d=r
d
o
r
l
d
o
r
l
o
d
r
l
总结:
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________
的个数来判断;
(2)根据性质,由_________________ 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
O
l
O
l
O
l
r
d
┐
┐
d
┐
d
直线与圆的位置关系判定方法:
无
切线
割线
直线名称
无
切点
交点
公共点名称
d > r
d = r
d < r
圆心到直线距离
d 与半径 r 关系
0
1
2
公共点个数
相离
相切
相交
直线和圆的位置关系
1、已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
3)若AB和⊙O相交,则 .
2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
三、练习与例题
0cm≤
2
1
0
3.直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相 交
相 切
相 离
1.根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
·
A
O
例
在 Rt△ABC 中,∠C = 90°,AC = 3 cm , BC = 4 cm , 以 C 为圆心,r 为半径的圆与 AB 有怎样的关系?为什么?(1)r = 2 cm ; (2) r = 2.4 cm ; (3) r = 3 cm .
A
C
B
D
解:
过 C 作 CD⊥AB 于 D,在 Rt △ABC 中,
根据三角形面积公式有
CD · AB = AC · BC
即圆心 C 到 AB 的距离 d = 2.4 cm.
(1) 当 r = 2 cm 时,
有 d > r ,因此⊙C 和 AB 相离.
(2) 当 r = 2.4 cm 时,
有 d = r ,因此⊙C 和 AB 相切.
(3) 当 r = 3 cm 时,
有 d < r ,因此⊙C 和 AB 相交.
练习(B组)
1、如图,在Rt△ABC中,∠C=90°,AB=5cm,
AC=3cm,以C为圆心的圆与AB
相切,则这个圆的半径是 cm。
2、如图,已知∠AOB=30°,M为OB上一点,
且OM=5cm,以M为圆心,r为半径的圆与
直线OA有怎样的位置关系?为什么?
①r=2cm;②r=4cm;③r=2.5cm。
3、直线L 和⊙O有公共点,则直线L与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。
12/5
相离
相交
相切
D
在⊙O中,经过半径OA的
外端点A作直线L⊥OA,
则圆心O到直线L的距离
是多少 ______,直线L和
⊙O有什么位置关系
_________.
思考:
.
O
A
OA
相切
L
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
几何应用:
∵OA⊥L ∴L是⊙O的切线
A
B
l
O
圆O与直线l相切,则过点A的直径A B与切线l有
怎样的位置关系?
垂直
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB
∴AB是⊙O的切线
.
O
A
L
将上页思考中的问题
反过来,如果L是⊙O
的切线,切点为A,那么
半径OA与直线L是不
是一定垂直呢
一定垂直
切线的性质定理:
圆的切线垂直于过切点的半径
拓展应用:
1.在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,以D为
圆心,DB长为半径作⊙D.试说明:AC是⊙D的切线.
F
2.AB是⊙O的弦,C是⊙O外一点,BC是⊙O的切线,AB交
过C点的直径于点D,OA⊥CD,试判断△BCD的形状,并
说明你的理由.
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E
作⊙O的切线交AC的延长线于点D,试判断△AED的
形状,并说明理由.
