2020-2021学年浙教版九年级下册数学 第2章 直线与圆的位置关系 达标检测卷(word版含答案)
文档属性
| 名称 | 2020-2021学年浙教版九年级下册数学 第2章 直线与圆的位置关系 达标检测卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 717.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览



文档简介
第2章达标检测卷
1.已知⊙O的直径是6,点O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相离
B.相切
C.相交
D.无法判断
2.平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线的条数为( )
A.0条
B.1条
C.2条
D.无数条
3.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD,若∠C=50°,则∠AOD的度数为( )
A.40°
B.50°
C.80°
D.100°
4.如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上的一点,DC是⊙O的切线,C是切点,连结AC,BC,若∠BCD=∠CAB=30°,则BD的长为( )
A.2R
B.R
C.R
D.R
5.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
6.如图,⊙O内切于△ABC,切点分别为D,E,F.∠B=50°,∠C=60°,连结OE,OF,DE,DF,则∠EDF等于( )
A.40°
B.55°
C.65°
D.70°
7.如图,AB为⊙O的直径,AD切⊙O于点A,=.则下列结论不一定正确的是( )
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC
8.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连结PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4
B.3
C.2
D.1
9.已知⊙O的半径为1,圆心O到直线l的距离为2,过l上任意一点A作⊙O的切线,切点为B,则线段AB长度的最小值为( )
A.1
B.
C.
D.2
10.如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A,E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM,ON,BM,BN.记△MNO,△AOM,△DMN的面积分别为S1,S2,S3,则下列结论不一定成立的是( )
A.S1>S2+S3
B.△AOM∽△DMN
C.∠MBN=45°
D.MN=AM+CN
二、填空题(每题3分,共24分)
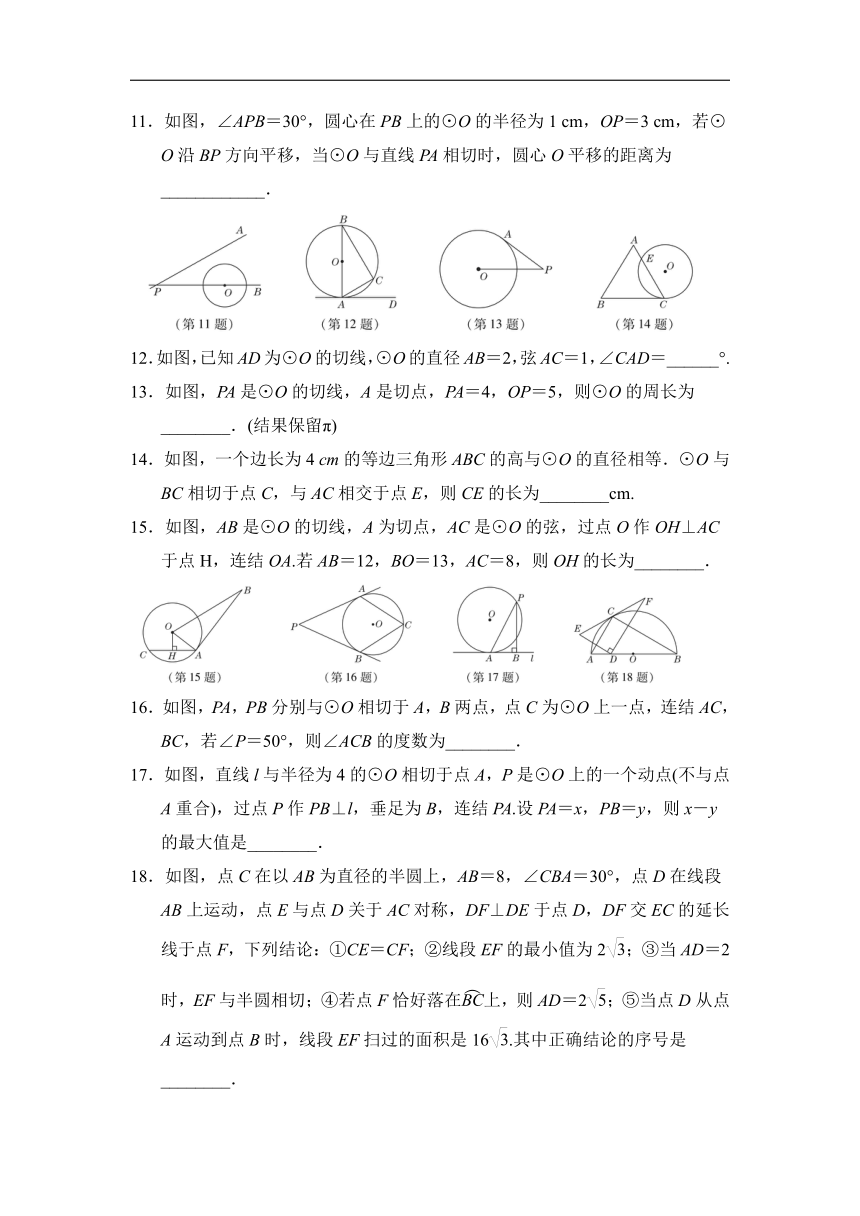
11.如图,∠APB=30°,圆心在PB上的⊙O的半径为1
cm,OP=3
cm,若⊙O沿BP方向平移,当⊙O与直线PA相切时,圆心O平移的距离为____________.
12.如图,已知AD为⊙O的切线,⊙O的直径AB=2,弦AC=1,∠CAD=______°.
13.如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为________.(结果保留π)
14.如图,一个边长为4
cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为________cm.
15.如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过点O作OH⊥AC于点H,连结OA.若AB=12,BO=13,AC=8,则OH的长为________.
16.如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连结AC,BC,若∠P=50°,则∠ACB的度数为________.
17.如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA.设PA=x,PB=y,则x-y的最大值是________.
18.如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,DF交EC的延长线于点F,下列结论:①CE=CF;②线段EF的最小值为2;③当AD=2时,EF与半圆相切;④若点F恰好落在上,则AD=2;⑤当点D从点A运动到点B时,线段EF扫过的面积是16.其中正确结论的序号是________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,在Rt△ABC中,∠ACB=90°.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.
20.如图,⊙O的半径为4,B是⊙O外一点,连结OB,且OB=6.过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求AC的长.
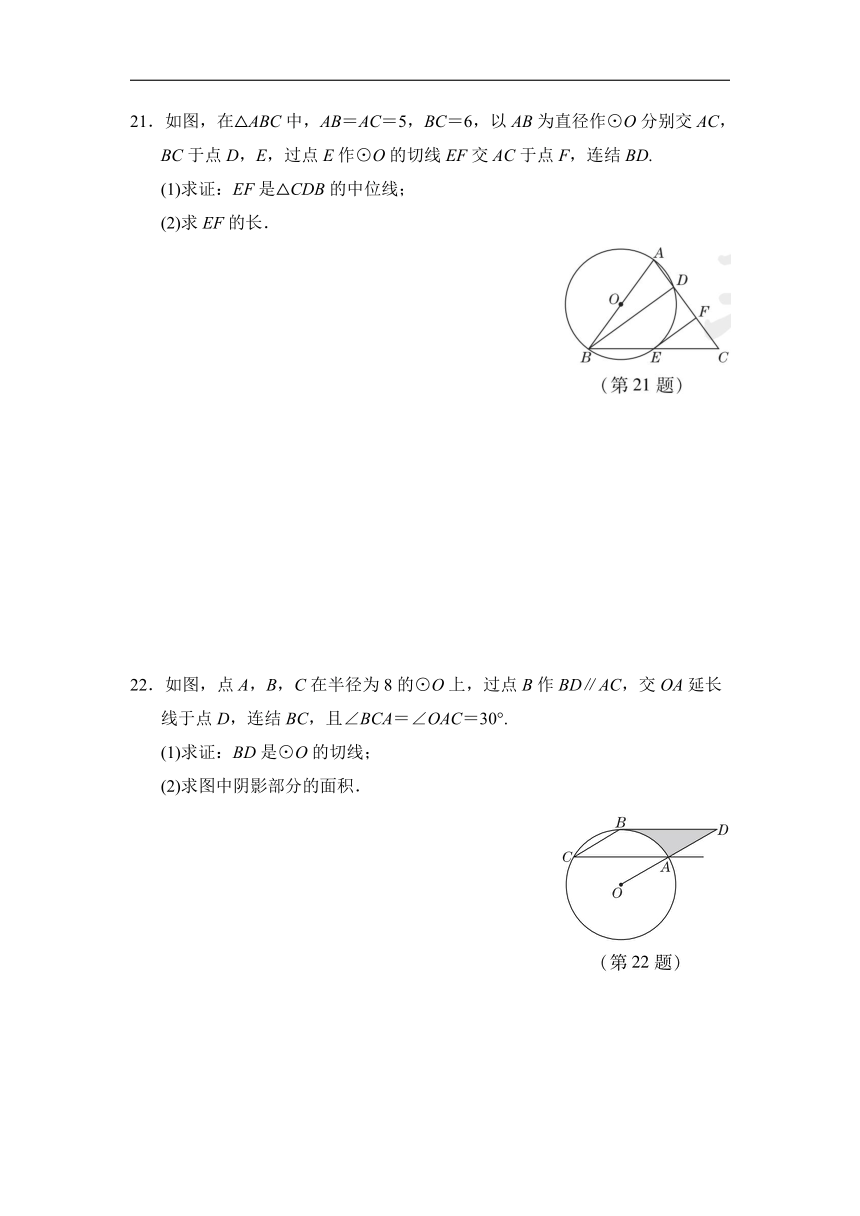
21.如图,在△ABC中,AB=AC=5,BC=6,以AB为直径作⊙O分别交AC,BC于点D,E,过点E作⊙O的切线EF交AC于点F,连结BD.
(1)求证:EF是△CDB的中位线;
(2)求EF的长.
22.如图,点A,B,C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D,连结BC,且∠BCA=∠OAC=30°.
(1)求证:BD是⊙O的切线;
(2)求图中阴影部分的面积.
23.如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连结OP交⊙O于E,过A点作AB⊥PO于点D,交⊙O于B,连结BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=,BC=1,求PO的长.
24.如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2
cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=4
cm,AD=4
cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3
cm/s,矩形ABCD的移动速度为4
cm/s,设移动时间为t
s.
(1)连结OA,AC,则∠OAC的度数为________°;
(2)两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达矩形A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离;
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)
答案
一、1.B 2.C 3.C
4.C 点拨:∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC=AB=R,∠ABC=60°.
∴∠CBD=120°,
则∠D=180°-∠CBD-∠BCD=30°.
∴BD=BC=R,故选C.
5.B
6.B 点拨:由∠B=50°,∠C=60°可求出∠A=70°,则易求得∠EOF=110°,∴∠EDF=∠EOF=55°.
7.D 8.A 9.C
10.A 点拨:如图①,作MF∥AO交ON于点F,
由点O是线段AE上的一个动点,当AM=MD时,
易证S1=S2+S3.故选项A不一定成立.
易证∠A=∠D=90°,∠AOM=∠DMN,
∴△AOM∽△DMN,故选项B成立.
如图②,作BP⊥MN于点P,
先证△MAB≌△MPB,
再证Rt△BPN≌Rt△BCN.
由此易得∠MBN=45°,MN=AM+CN.故选项C,D成立.综上所述,选项A不一定成立,故选A.
二、11.1
cm或5
cm 12.30 13.6π
14.3 点拨:过O作OF⊥AC于F,连结OC,如图.则CE=2CF.根据△ABC为等边三角形,且边长为4
cm,易求得它的高为2
cm,即OC=
cm.
∵BC与⊙O相切,∴∠OCB=90°.
又∠ACB=60°,
∴∠OCF=30°.
在Rt△OFC中,可得CF=OC·cos
30°=×=(cm),故CE=2CF=3
cm.
15.3 16.65°
17.2 点拨:如图,连结OA,过点O作OC⊥AP于点C,所以∠ACO=90°,AC=AP.易证△OAC∽△APB,所以=,即=,所以y=.
所以x-y=x-=-(x-4)2+2,所以x-y的最大值是2.
18.①③⑤
三、19.解:(1)如图所示.
(2)AB与⊙O相切.
证明:作OD⊥AB于点D,如图所示.
∵BO平分∠ABC,∠ACB=90°,OD⊥AB,∴OD=OC.∴AB与⊙O相切.
20.(1)证明:如图,连结OD.
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
∵AC⊥BC,∴OD∥AC,∴∠3=∠2.
又∵OD=OA,∴∠1=∠3,∴∠1=∠2.
∴AD平分∠BAC.
(2)解:∵OD∥AC,∴△BOD∽△BAC.
∴=,即=,解得AC=.
21.(1)证明:连结AE,OE,如图所示.
∵AB为⊙O的直径,
∴∠ADB=∠AEB=90°.
∴AE⊥BC,AC⊥BD.
∵AB=AC,BC=6,∴BE=CE=3.
∵OA=OB,∴OE是△ABC的中位线.
∴OE∥AC.∴OE⊥BD.
∵EF是⊙O的切线,∴OE⊥EF.
∴BD∥EF.
∵BE=CE,∴CF=DF.
∴EF是△CDB的中位线.
(2)解:∵∠AEB=90°,
∴AE===4.
∵△ABC的面积=AC·BD=BC·AE,∴BD===.
∵EF是△CDB的中位线,
∴EF=BD=.
22.(1)证明:如图,连结OB,交CA于点E.
∵∠C=30°,∠C=∠BOA,
∴∠BOA=60°.
∵∠OAC=30°,∴∠AEO=90°.
∵BD∥AC,∴∠DBE=∠AEO=90°.
∴OB⊥BD.∴BD是⊙O的切线.
(2)解:∵AC∥BD,
∴∠D=∠OAC=30°.
∵∠OBD=90°,OB=8,
∴BD=OB=8
.
∴S阴影=S△BDO-S扇形AOB=×8×8-=32-.
23.(1)证明:如图,连结OB.
∵AO=BO,AB⊥PO,
∴∠AOP=∠POB.
在△AOP和△BOP中,
∴△AOP≌△BOP(SAS).
∴∠OBP=∠OAP.
∵PA为⊙O的切线,∴∠OAP=90°.
∴∠OBP=90°,即OB⊥PB.
∴PB是⊙O的切线.
(2)证明:如图,连结AE.
∵PA为⊙O的切线,
∴∠PAE+∠OAE=90°.
∵AD⊥ED,∴∠EAD+∠AED=90°.
∵OE=OA,∴∠OAE=∠AED.
∴∠PAE=∠DAE,即AE平分∠PAD.
∵PA,PB为⊙O的切线,
∴PD平分∠APB,交∠PAD的平分线于点E.
∴E为△PAB的内心.
(3)解:∵PA为⊙O的切线,AC为⊙O的直径,
∴∠PAB+∠BAC=90°,∠C+∠BAC=90°.
∴∠PAB=∠C.
∴cos
C=cos∠PAB=.
在Rt△ABC中,cos
C===,
∴AC=.∴AO=.
∵∠DPA+∠PAD=90°,
∠PAD+∠BAC=90°,
∴∠DPA=∠BAC.
又∵∠PAO=∠ABC=90°,
∴△PAO∽△ABC.∴=.
∴PO=·AC=×=5.
24.解:(1)105
(2)当O1,A1,C1恰好在同一直线上时,设⊙O1与l1的切点为E,
连结OO1,O1E,可得O1E=2
cm,O1E⊥l1.
在Rt△A1D1C1中,
∵A1D1=4
cm,C1D1=4
cm,
∴tan
∠C1A1D1=,
∴∠C1A1D1=60°.
在Rt△A1O1E中,∠O1A1E=∠C1A1D1=60°,
∴A1E==(cm).
∵A1E=AA1-OO1-2=t-2(cm),
∴t-2=,
∴t=+2.
∴OO1=3t=(2+6)cm.
即圆心O移动的距离为(2+6)cm.
(3)①当直线AC与⊙O第一次相切时,设移动时间为t1
s,如图,此时⊙O移动到⊙O2的位置,矩形ABCD移动到矩形A2B2C2D2的位置.
设⊙O2与直线l1,A2C2分别相切于点F,G,连结O2F,O2G,O2A2,OO2,∴O2F⊥l1,O2G⊥A2C2.
由(2)得∠C2A2D2=60°,
∴∠GA2F=120°,
∴∠O2A2F=60°.
在Rt△A2O2F中,O2F=2
cm,
∴A2F=
cm.
∵OO2=3t1
cm,AF=AA2+A2F=cm,
∴4t1+-3t1=2,
解得t1=2-.
②当直线AC与⊙O第二次相切时,设移动时间为t2
s.
记第一次相切时为位置一,点O1,A1,C1共线时为位置二,第二次相切时为位置三.
由题意知,从位置一到位置二所用时间与从位置二到位置三所用时间相等.
∴+2-=t2-,
解得t2=2+2.
综上所述,当d<2时,t的取值范围是2-
1.已知⊙O的直径是6,点O到直线l的距离为3,则直线l与⊙O的位置关系是( )
A.相离
B.相切
C.相交
D.无法判断
2.平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线的条数为( )
A.0条
B.1条
C.2条
D.无数条
3.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD,若∠C=50°,则∠AOD的度数为( )
A.40°
B.50°
C.80°
D.100°
4.如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上的一点,DC是⊙O的切线,C是切点,连结AC,BC,若∠BCD=∠CAB=30°,则BD的长为( )
A.2R
B.R
C.R
D.R
5.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1
B.1或5
C.3
D.5
6.如图,⊙O内切于△ABC,切点分别为D,E,F.∠B=50°,∠C=60°,连结OE,OF,DE,DF,则∠EDF等于( )
A.40°
B.55°
C.65°
D.70°
7.如图,AB为⊙O的直径,AD切⊙O于点A,=.则下列结论不一定正确的是( )
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC
8.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连结PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4
B.3
C.2
D.1
9.已知⊙O的半径为1,圆心O到直线l的距离为2,过l上任意一点A作⊙O的切线,切点为B,则线段AB长度的最小值为( )
A.1
B.
C.
D.2
10.如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A,E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连结OM,ON,BM,BN.记△MNO,△AOM,△DMN的面积分别为S1,S2,S3,则下列结论不一定成立的是( )
A.S1>S2+S3
B.△AOM∽△DMN
C.∠MBN=45°
D.MN=AM+CN
二、填空题(每题3分,共24分)
11.如图,∠APB=30°,圆心在PB上的⊙O的半径为1
cm,OP=3
cm,若⊙O沿BP方向平移,当⊙O与直线PA相切时,圆心O平移的距离为____________.
12.如图,已知AD为⊙O的切线,⊙O的直径AB=2,弦AC=1,∠CAD=______°.
13.如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为________.(结果保留π)
14.如图,一个边长为4
cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为________cm.
15.如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过点O作OH⊥AC于点H,连结OA.若AB=12,BO=13,AC=8,则OH的长为________.
16.如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连结AC,BC,若∠P=50°,则∠ACB的度数为________.
17.如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA.设PA=x,PB=y,则x-y的最大值是________.
18.如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,DF交EC的延长线于点F,下列结论:①CE=CF;②线段EF的最小值为2;③当AD=2时,EF与半圆相切;④若点F恰好落在上,则AD=2;⑤当点D从点A运动到点B时,线段EF扫过的面积是16.其中正确结论的序号是________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.如图,在Rt△ABC中,∠ACB=90°.
(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.
20.如图,⊙O的半径为4,B是⊙O外一点,连结OB,且OB=6.过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
(1)求证:AD平分∠BAC;
(2)求AC的长.
21.如图,在△ABC中,AB=AC=5,BC=6,以AB为直径作⊙O分别交AC,BC于点D,E,过点E作⊙O的切线EF交AC于点F,连结BD.
(1)求证:EF是△CDB的中位线;
(2)求EF的长.
22.如图,点A,B,C在半径为8的⊙O上,过点B作BD∥AC,交OA延长线于点D,连结BC,且∠BCA=∠OAC=30°.
(1)求证:BD是⊙O的切线;
(2)求图中阴影部分的面积.
23.如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连结OP交⊙O于E,过A点作AB⊥PO于点D,交⊙O于B,连结BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=,BC=1,求PO的长.
24.如图,已知l1⊥l2,⊙O与l1,l2都相切,⊙O的半径为2
cm.矩形ABCD的边AD,AB分别与l1,l2重合,AB=4
cm,AD=4
cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3
cm/s,矩形ABCD的移动速度为4
cm/s,设移动时间为t
s.
(1)连结OA,AC,则∠OAC的度数为________°;
(2)两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达矩形A1B1C1D1的位置,此时点O1,A1,C1恰好在同一直线上,求圆心O移动的距离;
(3)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围.(解答时可以利用备用图画出相关示意图)
答案
一、1.B 2.C 3.C
4.C 点拨:∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠CAB=30°,
∴BC=AB=R,∠ABC=60°.
∴∠CBD=120°,
则∠D=180°-∠CBD-∠BCD=30°.
∴BD=BC=R,故选C.
5.B
6.B 点拨:由∠B=50°,∠C=60°可求出∠A=70°,则易求得∠EOF=110°,∴∠EDF=∠EOF=55°.
7.D 8.A 9.C
10.A 点拨:如图①,作MF∥AO交ON于点F,
由点O是线段AE上的一个动点,当AM=MD时,
易证S1=S2+S3.故选项A不一定成立.
易证∠A=∠D=90°,∠AOM=∠DMN,
∴△AOM∽△DMN,故选项B成立.
如图②,作BP⊥MN于点P,
先证△MAB≌△MPB,
再证Rt△BPN≌Rt△BCN.
由此易得∠MBN=45°,MN=AM+CN.故选项C,D成立.综上所述,选项A不一定成立,故选A.
二、11.1
cm或5
cm 12.30 13.6π
14.3 点拨:过O作OF⊥AC于F,连结OC,如图.则CE=2CF.根据△ABC为等边三角形,且边长为4
cm,易求得它的高为2
cm,即OC=
cm.
∵BC与⊙O相切,∴∠OCB=90°.
又∠ACB=60°,
∴∠OCF=30°.
在Rt△OFC中,可得CF=OC·cos
30°=×=(cm),故CE=2CF=3
cm.
15.3 16.65°
17.2 点拨:如图,连结OA,过点O作OC⊥AP于点C,所以∠ACO=90°,AC=AP.易证△OAC∽△APB,所以=,即=,所以y=.
所以x-y=x-=-(x-4)2+2,所以x-y的最大值是2.
18.①③⑤
三、19.解:(1)如图所示.
(2)AB与⊙O相切.
证明:作OD⊥AB于点D,如图所示.
∵BO平分∠ABC,∠ACB=90°,OD⊥AB,∴OD=OC.∴AB与⊙O相切.
20.(1)证明:如图,连结OD.
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
∵AC⊥BC,∴OD∥AC,∴∠3=∠2.
又∵OD=OA,∴∠1=∠3,∴∠1=∠2.
∴AD平分∠BAC.
(2)解:∵OD∥AC,∴△BOD∽△BAC.
∴=,即=,解得AC=.
21.(1)证明:连结AE,OE,如图所示.
∵AB为⊙O的直径,
∴∠ADB=∠AEB=90°.
∴AE⊥BC,AC⊥BD.
∵AB=AC,BC=6,∴BE=CE=3.
∵OA=OB,∴OE是△ABC的中位线.
∴OE∥AC.∴OE⊥BD.
∵EF是⊙O的切线,∴OE⊥EF.
∴BD∥EF.
∵BE=CE,∴CF=DF.
∴EF是△CDB的中位线.
(2)解:∵∠AEB=90°,
∴AE===4.
∵△ABC的面积=AC·BD=BC·AE,∴BD===.
∵EF是△CDB的中位线,
∴EF=BD=.
22.(1)证明:如图,连结OB,交CA于点E.
∵∠C=30°,∠C=∠BOA,
∴∠BOA=60°.
∵∠OAC=30°,∴∠AEO=90°.
∵BD∥AC,∴∠DBE=∠AEO=90°.
∴OB⊥BD.∴BD是⊙O的切线.
(2)解:∵AC∥BD,
∴∠D=∠OAC=30°.
∵∠OBD=90°,OB=8,
∴BD=OB=8
.
∴S阴影=S△BDO-S扇形AOB=×8×8-=32-.
23.(1)证明:如图,连结OB.
∵AO=BO,AB⊥PO,
∴∠AOP=∠POB.
在△AOP和△BOP中,
∴△AOP≌△BOP(SAS).
∴∠OBP=∠OAP.
∵PA为⊙O的切线,∴∠OAP=90°.
∴∠OBP=90°,即OB⊥PB.
∴PB是⊙O的切线.
(2)证明:如图,连结AE.
∵PA为⊙O的切线,
∴∠PAE+∠OAE=90°.
∵AD⊥ED,∴∠EAD+∠AED=90°.
∵OE=OA,∴∠OAE=∠AED.
∴∠PAE=∠DAE,即AE平分∠PAD.
∵PA,PB为⊙O的切线,
∴PD平分∠APB,交∠PAD的平分线于点E.
∴E为△PAB的内心.
(3)解:∵PA为⊙O的切线,AC为⊙O的直径,
∴∠PAB+∠BAC=90°,∠C+∠BAC=90°.
∴∠PAB=∠C.
∴cos
C=cos∠PAB=.
在Rt△ABC中,cos
C===,
∴AC=.∴AO=.
∵∠DPA+∠PAD=90°,
∠PAD+∠BAC=90°,
∴∠DPA=∠BAC.
又∵∠PAO=∠ABC=90°,
∴△PAO∽△ABC.∴=.
∴PO=·AC=×=5.
24.解:(1)105
(2)当O1,A1,C1恰好在同一直线上时,设⊙O1与l1的切点为E,
连结OO1,O1E,可得O1E=2
cm,O1E⊥l1.
在Rt△A1D1C1中,
∵A1D1=4
cm,C1D1=4
cm,
∴tan
∠C1A1D1=,
∴∠C1A1D1=60°.
在Rt△A1O1E中,∠O1A1E=∠C1A1D1=60°,
∴A1E==(cm).
∵A1E=AA1-OO1-2=t-2(cm),
∴t-2=,
∴t=+2.
∴OO1=3t=(2+6)cm.
即圆心O移动的距离为(2+6)cm.
(3)①当直线AC与⊙O第一次相切时,设移动时间为t1
s,如图,此时⊙O移动到⊙O2的位置,矩形ABCD移动到矩形A2B2C2D2的位置.
设⊙O2与直线l1,A2C2分别相切于点F,G,连结O2F,O2G,O2A2,OO2,∴O2F⊥l1,O2G⊥A2C2.
由(2)得∠C2A2D2=60°,
∴∠GA2F=120°,
∴∠O2A2F=60°.
在Rt△A2O2F中,O2F=2
cm,
∴A2F=
cm.
∵OO2=3t1
cm,AF=AA2+A2F=cm,
∴4t1+-3t1=2,
解得t1=2-.
②当直线AC与⊙O第二次相切时,设移动时间为t2
s.
记第一次相切时为位置一,点O1,A1,C1共线时为位置二,第二次相切时为位置三.
由题意知,从位置一到位置二所用时间与从位置二到位置三所用时间相等.
∴+2-=t2-,
解得t2=2+2.
综上所述,当d<2时,t的取值范围是2-
