2020-2021学年浙教版九年级下册数学 第3章投影与三视图达标检测卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年浙教版九年级下册数学 第3章投影与三视图达标检测卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 495.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 19:18:07 | ||
图片预览

文档简介
第3章达标检测卷
一、选择题(每题3分,共30分)
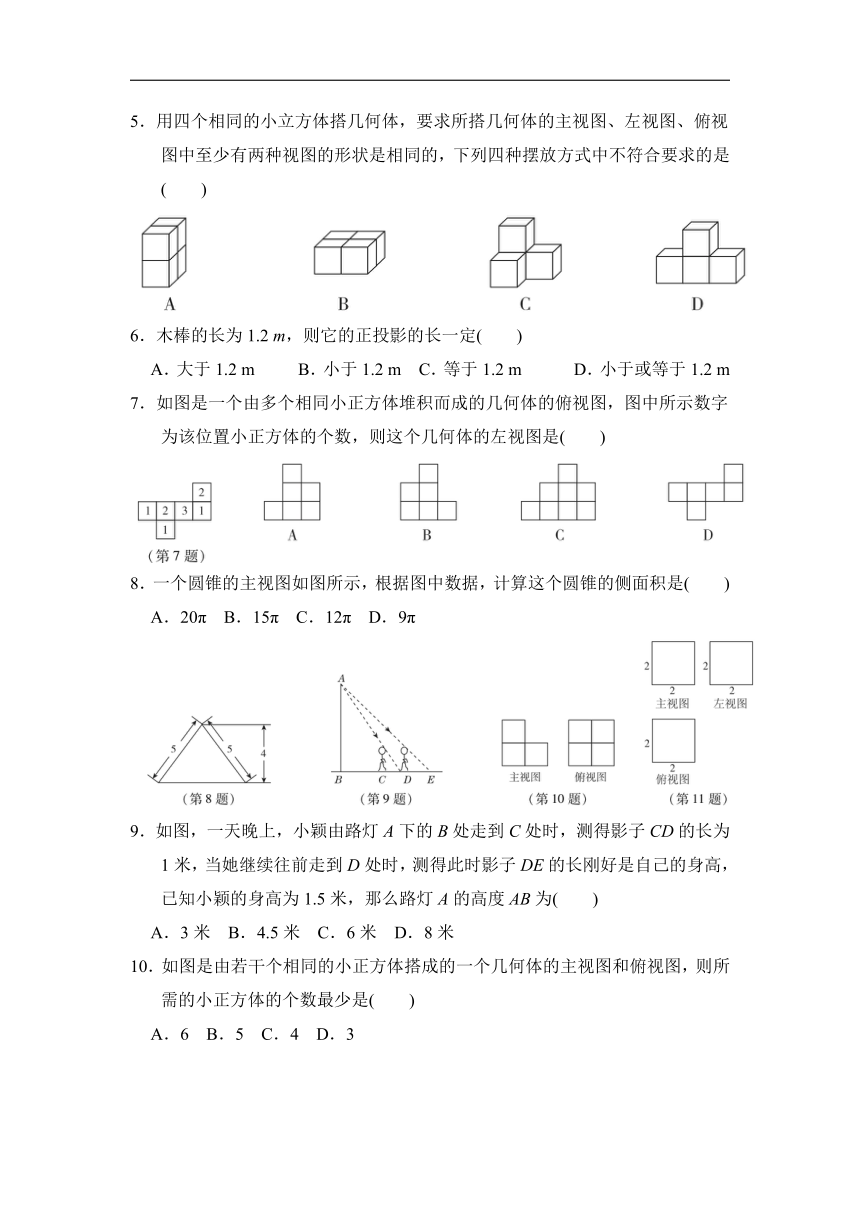
1.如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )
2.下列四个几何体中,俯视图为四边形的是( )
3.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影是一个圆面,当把球向上平移时,圆面的大小变化是( )
A.越来越小
B.越来越大
C.大小不变
D.不能确定
4.如图是一个长方体包装盒,则它的表面展开图是( )
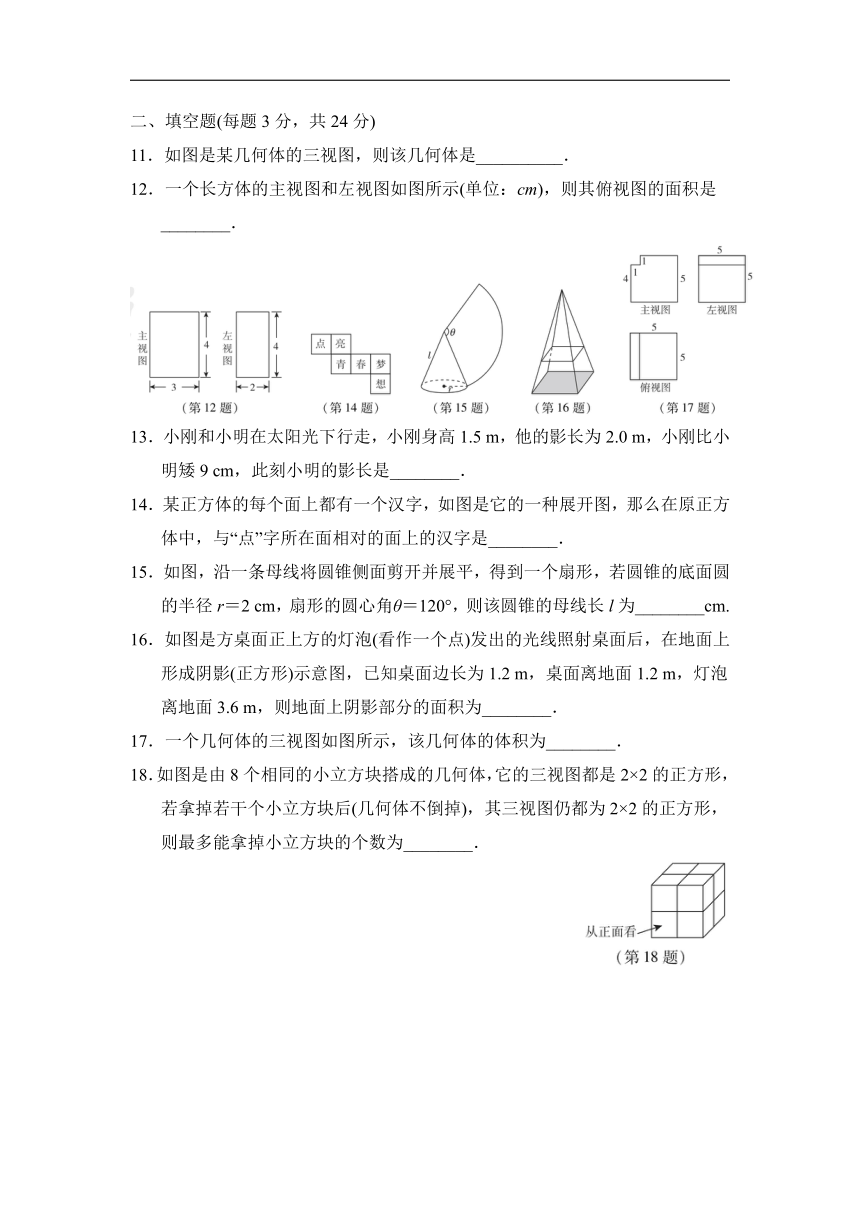
5.用四个相同的小立方体搭几何体,要求所搭几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是( )
6.木棒的长为1.2
m,则它的正投影的长一定( )
A.大于1.2
m
B.小于1.2
m
C.等于1.2
m D.小于或等于1.2
m
7.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的左视图是( )
8.一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是( )
A.20π
B.15π
C.12π
D.9π
9.如图,一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得此时影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
A.3米
B.4.5米
C.6米
D.8米
10.如图是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图,则所需的小正方体的个数最少是( )
A.6
B.5
C.4
D.3
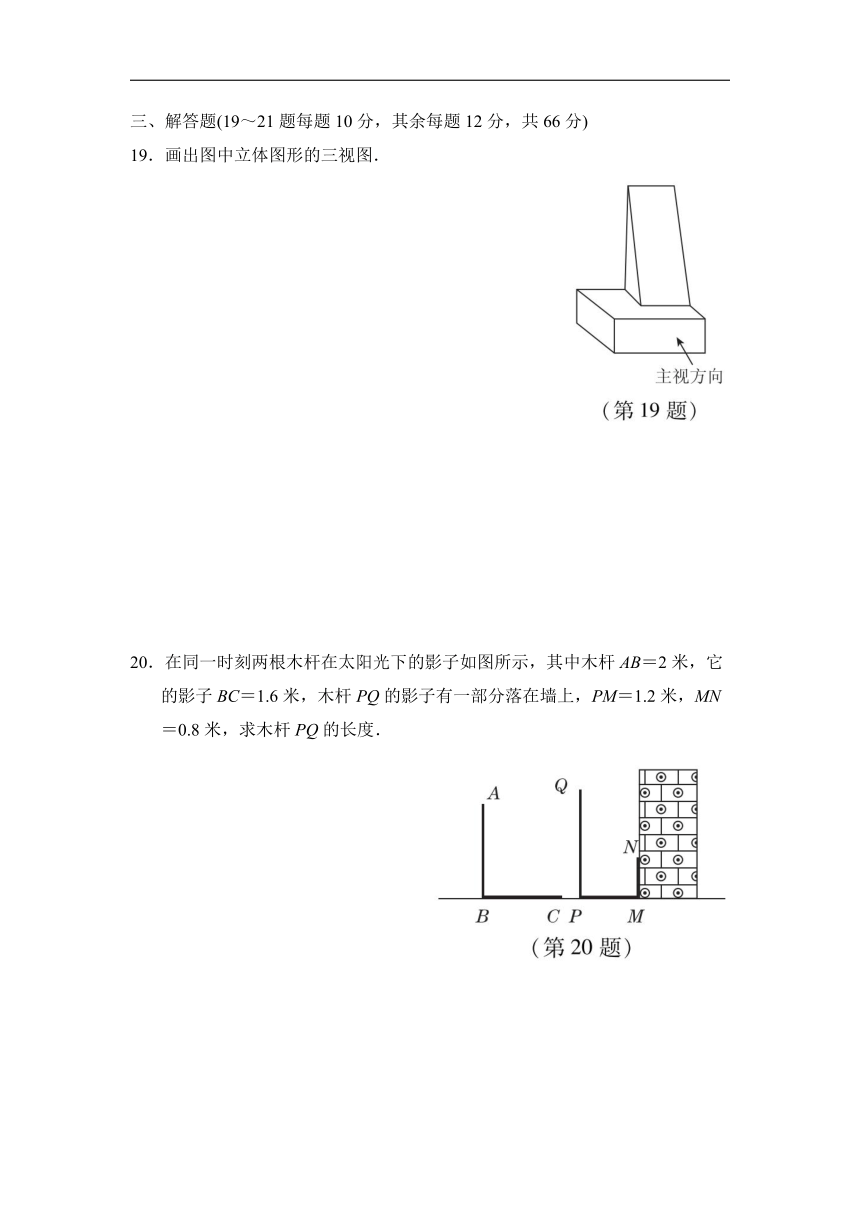
二、填空题(每题3分,共24分)
11.如图是某几何体的三视图,则该几何体是__________.
12.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是________.
13.小刚和小明在太阳光下行走,小刚身高1.5
m,他的影长为2.0
m,小刚比小明矮9
cm,此刻小明的影长是________.
14.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对的面上的汉字是________.
15.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2
cm,扇形的圆心角θ=120°,则该圆锥的母线长l为________cm.
16.如图是方桌面正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(正方形)示意图,已知桌面边长为1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为________.
17.一个几何体的三视图如图所示,该几何体的体积为________.
18.如图是由8个相同的小立方块搭成的几何体,它的三视图都是2×2的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三视图仍都为2×2的正方形,则最多能拿掉小立方块的个数为________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.画出图中立体图形的三视图.
20.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.
21.如图,圆柱形容器的高为1.2
m,底面周长为1
m,在容器内壁离容器底部0.3
m的点B处有一只蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3
m与蚊子相对的点A处,求壁虎捕捉蚊子所走的最短路程.(容器厚度忽略不计)
22.如图,在⊙O中,AB=4
,AC是⊙O的直径,AC⊥BD于点F,∠A=30°.
(1)求图中阴影部分的面积;
(2)若用阴影扇形BOD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
23.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的全面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
24.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗户距地面的高度OD=0.8
m,窗高CD=1.2
m,并测得OE=0.8
m,OF=3
m,求围墙AB的高度.
答案
一、1.D 2.D 3.B 4.A 5.D
6.D 点拨:正投影的长度与木棒的摆放位置有关系,但无论怎样摆,正投影的长都不会超过1.2
m.故选D.
7.B 8.B 9.B 10.B
二、11.正方体 12.6
cm2 13.2.12
m 14.春 15.6 16.3.24
m2
17.120 18.2
三、19.解:如图所示.
20.解:==,PM+=1.2+0.8×=1.84,易知=,
解得PQ=2.3.
答:木杆PQ的长度为2.3米.
21.解:因为壁虎与蚊子在相对的位置上,所以若沿蚊子所在的母线将圆柱形容器的侧面展开,则壁虎在展开图矩形相对两边中点的连线上,如图所示.要求壁虎捕捉蚊子的最短距离,实际上是在EF上找一点P,使PA+PB的值最小.求这个最小值,于是作点A关于EF的对称点A′,连结A′B,则A′B与EF的交点就是点P,过B作BM⊥AA′于点M.易知A′M=1.2
m,BM=0.5
m,所以在Rt△A′MB中,A′B==1.3
m,因为A′B=A′P+PB=AP+PB,所以壁虎捕捉蚊子所走的最短路程为1.3
m.
22.解:(1)由已知,易求得OB=4,∠BOD=120°.∴S阴影=×π×42=π.
(2)设围成圆锥底面圆的半径为r,则
×π×4=2πr,解得r=.
23.解:(1)圆锥
(2)全面积S=12π+4π=16π.
(3)如图将圆锥侧面展开,易知C为弧BB′中点,线段BD为所求的最短路程.由条件易得,∠BAB′=120°,AC⊥BB′,∠BAC=∠BAB′,所以∠BAD=60°,所以BD=ABsin
60°=3.
24.解:由题意可知OD=OE,
∠DOE=90°,∴∠DEO=45°.
又∵∠ABE=90°,∴∠BAE=45°.
∴AB=BE,即AB=BO+OE.
连结CD,易知C,D,O三点在同一直线上.在△ABF和△COF中,∠ABF=∠COF=90°,∠AFB=∠CFO,
∴△ABF∽△COF.∴=,
即=.
∴=.∴BO=3.6.经检验BO=3.6是方程的解,
∴AB=3.6+0.8=4.4,即围墙AB的高度为4.4
m.
一、选择题(每题3分,共30分)
1.如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )
2.下列四个几何体中,俯视图为四边形的是( )
3.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影是一个圆面,当把球向上平移时,圆面的大小变化是( )
A.越来越小
B.越来越大
C.大小不变
D.不能确定
4.如图是一个长方体包装盒,则它的表面展开图是( )
5.用四个相同的小立方体搭几何体,要求所搭几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是( )
6.木棒的长为1.2
m,则它的正投影的长一定( )
A.大于1.2
m
B.小于1.2
m
C.等于1.2
m D.小于或等于1.2
m
7.如图是一个由多个相同小正方体堆积而成的几何体的俯视图,图中所示数字为该位置小正方体的个数,则这个几何体的左视图是( )
8.一个圆锥的主视图如图所示,根据图中数据,计算这个圆锥的侧面积是( )
A.20π
B.15π
C.12π
D.9π
9.如图,一天晚上,小颖由路灯A下的B处走到C处时,测得影子CD的长为1米,当她继续往前走到D处时,测得此时影子DE的长刚好是自己的身高,已知小颖的身高为1.5米,那么路灯A的高度AB为( )
A.3米
B.4.5米
C.6米
D.8米
10.如图是由若干个相同的小正方体搭成的一个几何体的主视图和俯视图,则所需的小正方体的个数最少是( )
A.6
B.5
C.4
D.3
二、填空题(每题3分,共24分)
11.如图是某几何体的三视图,则该几何体是__________.
12.一个长方体的主视图和左视图如图所示(单位:cm),则其俯视图的面积是________.
13.小刚和小明在太阳光下行走,小刚身高1.5
m,他的影长为2.0
m,小刚比小明矮9
cm,此刻小明的影长是________.
14.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对的面上的汉字是________.
15.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2
cm,扇形的圆心角θ=120°,则该圆锥的母线长l为________cm.
16.如图是方桌面正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(正方形)示意图,已知桌面边长为1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为________.
17.一个几何体的三视图如图所示,该几何体的体积为________.
18.如图是由8个相同的小立方块搭成的几何体,它的三视图都是2×2的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三视图仍都为2×2的正方形,则最多能拿掉小立方块的个数为________.
三、解答题(19~21题每题10分,其余每题12分,共66分)
19.画出图中立体图形的三视图.
20.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.
21.如图,圆柱形容器的高为1.2
m,底面周长为1
m,在容器内壁离容器底部0.3
m的点B处有一只蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3
m与蚊子相对的点A处,求壁虎捕捉蚊子所走的最短路程.(容器厚度忽略不计)
22.如图,在⊙O中,AB=4
,AC是⊙O的直径,AC⊥BD于点F,∠A=30°.
(1)求图中阴影部分的面积;
(2)若用阴影扇形BOD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
23.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的全面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个线路的最短路程.
24.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗户距地面的高度OD=0.8
m,窗高CD=1.2
m,并测得OE=0.8
m,OF=3
m,求围墙AB的高度.
答案
一、1.D 2.D 3.B 4.A 5.D
6.D 点拨:正投影的长度与木棒的摆放位置有关系,但无论怎样摆,正投影的长都不会超过1.2
m.故选D.
7.B 8.B 9.B 10.B
二、11.正方体 12.6
cm2 13.2.12
m 14.春 15.6 16.3.24
m2
17.120 18.2
三、19.解:如图所示.
20.解:==,PM+=1.2+0.8×=1.84,易知=,
解得PQ=2.3.
答:木杆PQ的长度为2.3米.
21.解:因为壁虎与蚊子在相对的位置上,所以若沿蚊子所在的母线将圆柱形容器的侧面展开,则壁虎在展开图矩形相对两边中点的连线上,如图所示.要求壁虎捕捉蚊子的最短距离,实际上是在EF上找一点P,使PA+PB的值最小.求这个最小值,于是作点A关于EF的对称点A′,连结A′B,则A′B与EF的交点就是点P,过B作BM⊥AA′于点M.易知A′M=1.2
m,BM=0.5
m,所以在Rt△A′MB中,A′B==1.3
m,因为A′B=A′P+PB=AP+PB,所以壁虎捕捉蚊子所走的最短路程为1.3
m.
22.解:(1)由已知,易求得OB=4,∠BOD=120°.∴S阴影=×π×42=π.
(2)设围成圆锥底面圆的半径为r,则
×π×4=2πr,解得r=.
23.解:(1)圆锥
(2)全面积S=12π+4π=16π.
(3)如图将圆锥侧面展开,易知C为弧BB′中点,线段BD为所求的最短路程.由条件易得,∠BAB′=120°,AC⊥BB′,∠BAC=∠BAB′,所以∠BAD=60°,所以BD=ABsin
60°=3.
24.解:由题意可知OD=OE,
∠DOE=90°,∴∠DEO=45°.
又∵∠ABE=90°,∴∠BAE=45°.
∴AB=BE,即AB=BO+OE.
连结CD,易知C,D,O三点在同一直线上.在△ABF和△COF中,∠ABF=∠COF=90°,∠AFB=∠CFO,
∴△ABF∽△COF.∴=,
即=.
∴=.∴BO=3.6.经检验BO=3.6是方程的解,
∴AB=3.6+0.8=4.4,即围墙AB的高度为4.4
m.
