浙教版 八下 第四章平行四边形单元测试卷(word版含答案)
文档属性
| 名称 | 浙教版 八下 第四章平行四边形单元测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 279.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 17:21:24 | ||
图片预览



文档简介
第四章平行四边形单元测试
一、单选题
1.如图,在中,,,,D、E分别是、的中点,则的长为( )
A.3 B.2.5 C.4 D.3.5
2.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC于E,AB=,AC=2,BD=4,则AE的长为( )
A. B. C. D.
3.如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S?ABCD=a,S?EFGH=b(a<b),则S阴影为( )
A.b﹣a B.(b﹣a) C.a D.b
4.如图在中,,点C关于的对称点为E,连接交于点F,点G为的中点,连接,.则的面积为( )
A. B. C. D.
5.已知点P关于原点的对称点为,则点P的坐标为( )
A. B. C. D.
6.如图所示,在中,,,分别是,,的中点,,,则四边形的周长是( )
A.10 B.20 C.30 D.40
7.如图,EF过对角线的交点O,并交于E,交于F,若,,,则四边形EFCD的周长是( )
A.16 B.14 C.12 D.10
8.如图,小峰从点O出发,前进后向右转45°,再前进后又向右转45°,…,这样一直走下去,他第一次回到出发点O时,一共走的路程是( )
A.35米 B.42米 C.70米 D.56米
9.如图,在中,,为垂足,如果,那么的度数是( )
A.80° B.30° C.40° D.50°
10.如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
二、填空题
11.如图,?ABCD的面积为32,E,F分别为AB、AD的中点,则的面积为_____.
12.如图,AE平分∠BAC,DE平分∠BDC,已知∠B=10°,∠C=40°,则∠E=____________.
13.若点与点关于原点成中心对称,则的值为___________.
14.已知的周长为56,自顶点A作于点E,于点F,若,,则_________________.
15.已知平行四边形相邻两边长相差2,这组邻边上的高线长之比为,则此平行四边形的周长为_____.
16.如图所示,正五边形中的度数为________.
三、解答题
17.在中,是对角线,于点E,于点F.
(1)求证:;
(2)试判断四边形是不是平行四边形,并说明理由.
18.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
19.如图,在平行四边形中,对角线与相交于点O,延长到点E,使,连接.
(1)求证:四边形是平行四边形;
(2)已知,,若,求的周长.
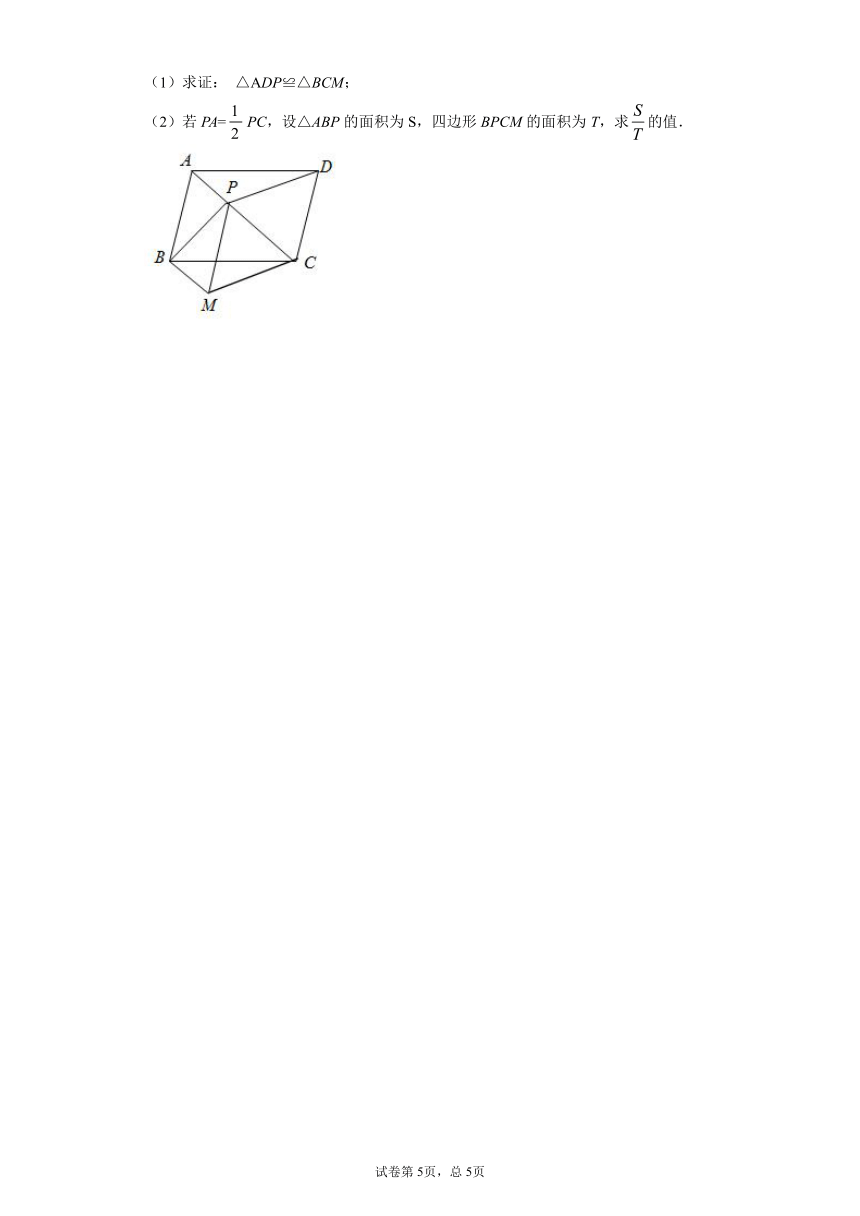
20.如图,在□ ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证: △ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
参考答案
1.B
2.D
3.D
4.B
5.D
6.A
7.C
8.D
9.B
10.A
11.12
12.15°
13.
14.4+或4-
15.12
16.36°
17.(1)见解析;(2)是,理由见解析
【详解】
解:(1)△ABE≌△CDF,理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEB=∠CFD=90°.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△DCF中,
,
∴△ABE≌△CDF(AAS);
(2)四边形AECF是平行四边形.
理由如下:∵△ABE≌△CDF(AAS),
∴AE=CF,
∵AE⊥BD于点E,CF⊥BD于点F,
∴AE//CF,
∴四边形AECF是平行四边形.
18.(1)证明见解析;(2).
【详解】
解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
19.(1)见解析;(2)24
【详解】
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵CE=BC,
∴AD=CE=BC,
∵AD∥BC,
∴AD∥CE,
∴四边形ACED是平行四边形;
(2)∵四边形ACED是平行四边形,
∴DE=AC=6,
∵CD=BC=CE=BE,
∴∠CBD=∠CDB,∠CDE=∠CED,
∴∠BDE=∠CDB+∠CDE==90°,
∴BE=2CD=2AB=10,
∴BD==8,
∴△BDE的周长=BD+BE+DE=8+10+6=24.
20.(1)证明见解析;(2)
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
一、单选题
1.如图,在中,,,,D、E分别是、的中点,则的长为( )
A.3 B.2.5 C.4 D.3.5
2.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC于E,AB=,AC=2,BD=4,则AE的长为( )
A. B. C. D.
3.如图,平行四边形纸片ABCD和EFGH上下叠放,AD∥EH且AD=EH,CE交GH于点O,已知S?ABCD=a,S?EFGH=b(a<b),则S阴影为( )
A.b﹣a B.(b﹣a) C.a D.b
4.如图在中,,点C关于的对称点为E,连接交于点F,点G为的中点,连接,.则的面积为( )
A. B. C. D.
5.已知点P关于原点的对称点为,则点P的坐标为( )
A. B. C. D.
6.如图所示,在中,,,分别是,,的中点,,,则四边形的周长是( )
A.10 B.20 C.30 D.40
7.如图,EF过对角线的交点O,并交于E,交于F,若,,,则四边形EFCD的周长是( )
A.16 B.14 C.12 D.10
8.如图,小峰从点O出发,前进后向右转45°,再前进后又向右转45°,…,这样一直走下去,他第一次回到出发点O时,一共走的路程是( )
A.35米 B.42米 C.70米 D.56米
9.如图,在中,,为垂足,如果,那么的度数是( )
A.80° B.30° C.40° D.50°
10.如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
二、填空题
11.如图,?ABCD的面积为32,E,F分别为AB、AD的中点,则的面积为_____.
12.如图,AE平分∠BAC,DE平分∠BDC,已知∠B=10°,∠C=40°,则∠E=____________.
13.若点与点关于原点成中心对称,则的值为___________.
14.已知的周长为56,自顶点A作于点E,于点F,若,,则_________________.
15.已知平行四边形相邻两边长相差2,这组邻边上的高线长之比为,则此平行四边形的周长为_____.
16.如图所示,正五边形中的度数为________.
三、解答题
17.在中,是对角线,于点E,于点F.
(1)求证:;
(2)试判断四边形是不是平行四边形,并说明理由.
18.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
19.如图,在平行四边形中,对角线与相交于点O,延长到点E,使,连接.
(1)求证:四边形是平行四边形;
(2)已知,,若,求的周长.
20.如图,在□ ABCD中,点P在对角线AC上一动点,过点P作PM//DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证: △ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
参考答案
1.B
2.D
3.D
4.B
5.D
6.A
7.C
8.D
9.B
10.A
11.12
12.15°
13.
14.4+或4-
15.12
16.36°
17.(1)见解析;(2)是,理由见解析
【详解】
解:(1)△ABE≌△CDF,理由如下:
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEB=∠CFD=90°.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
在△ABE与△DCF中,
,
∴△ABE≌△CDF(AAS);
(2)四边形AECF是平行四边形.
理由如下:∵△ABE≌△CDF(AAS),
∴AE=CF,
∵AE⊥BD于点E,CF⊥BD于点F,
∴AE//CF,
∴四边形AECF是平行四边形.
18.(1)证明见解析;(2).
【详解】
解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
19.(1)见解析;(2)24
【详解】
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵CE=BC,
∴AD=CE=BC,
∵AD∥BC,
∴AD∥CE,
∴四边形ACED是平行四边形;
(2)∵四边形ACED是平行四边形,
∴DE=AC=6,
∵CD=BC=CE=BE,
∴∠CBD=∠CDB,∠CDE=∠CED,
∴∠BDE=∠CDB+∠CDE==90°,
∴BE=2CD=2AB=10,
∴BD==8,
∴△BDE的周长=BD+BE+DE=8+10+6=24.
20.(1)证明见解析;(2)
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ADC+∠BCD=,
∵PM//DC,且PM=DC,
∴四边形PMCD是平行四边形,
∴PD=CM,∠PDC+∠DCM=,
∴∠ADP=∠BCM,
∴△ADP≌△BCM;
(2)解:作BH⊥AC于H,DG⊥AC于G,
∵四边形ABCD是平行四边形,
∴△ABC≌△CDA,
∴BH=DG,
∴,即,
,即,
∵△ADP≌△BCM,
∴,
∴=.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
