浙教版 九下 第二章直线与圆的位置关系单元测试卷(word版含答案)
文档属性
| 名称 | 浙教版 九下 第二章直线与圆的位置关系单元测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 578.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 17:27:24 | ||
图片预览


文档简介
第二章直线与圆的位置关系单元测试
一、单选题(共40分)
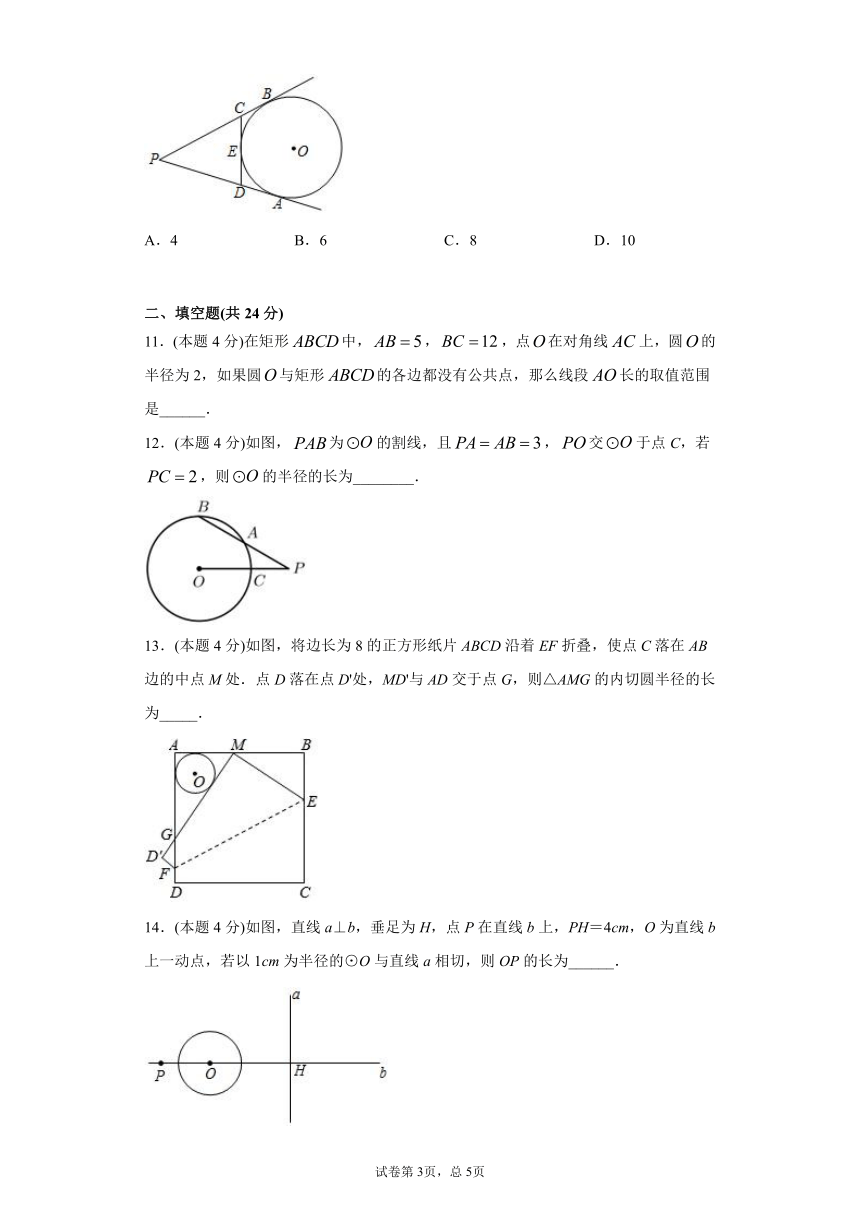
1.(本题4分)如图,是的直径,切于点T.若,则的度数为( )
A.52° B.54° C.56° D.76°
2.(本题4分)如图,中,,,,以斜边上的一点为圆心所作的半圆分别与相切于点,则为( )
A.2.5 B.1.6 C.1.5 D.2.6
3.(本题4分)如图,中,,,,以点为圆心,为半径作,当时,与的位置关系是( )
A.相切 B.相离 C.相交 D.无法确定
4.(本题4分)如图,分别切与点A,B,切于点C,分别交于点M,N,若,则的周长是( )
A. B. C. D.
5.(本题4分)中,斜边,其重心与外心之间的距离为( )
A.2 B.3 C.4 D.6
6.(本题4分)如图.PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OB,OP,AB.若 OA=1,∠APB=60°,则△PAB 的周长为( )
A.2 B.4 C.3 D.2+2
7.(本题4分)若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为,则实数a的值为( )
A.0或4 B.0或3
C.-2或6 D.-1或
8.(本题4分)如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )
A.35° B.45° C.65° D.70°
9.(本题4分)如图,菱形OABC的顶点A,B,C在上,过点B作的切线交OA的延长线于点D,若的半径为1,则BD的长为( )
A.1 B. C. D.2
10.(本题4分)如图,P是⊙O外一点,射线PA、PB分别切⊙O于点A、点B,CD切⊙O于点E,分别交PA、PB于点D、点C,若PB=4,则△PCD的周长( )
A.4 B.6 C.8 D.10
二、填空题(共24分)
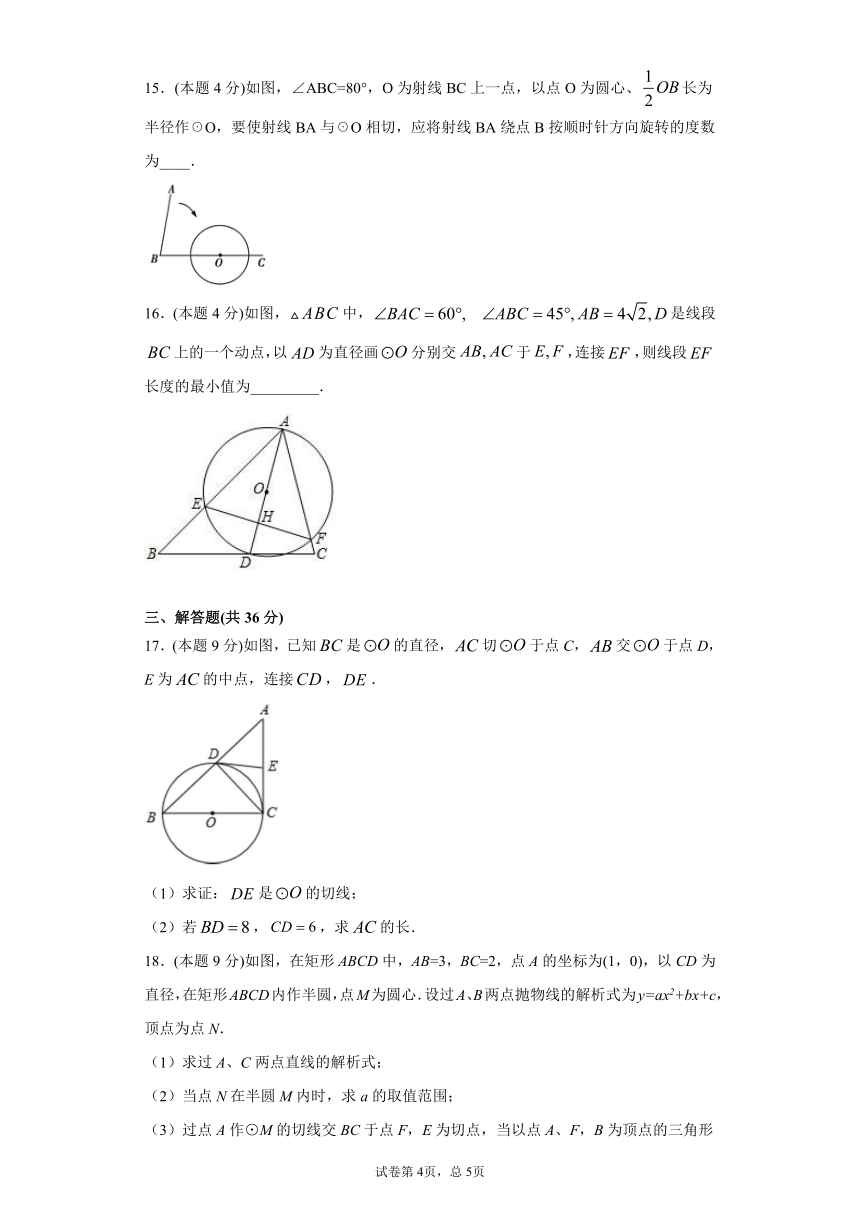
11.(本题4分)在矩形中,,,点在对角线上,圆的半径为2,如果圆与矩形的各边都没有公共点,那么线段长的取值范围是______.
12.(本题4分)如图,为的割线,且,交于点C,若,则的半径的长为________.
13.(本题4分)如图,将边长为8的正方形纸片ABCD沿着EF折叠,使点C落在AB边的中点M处.点D落在点D'处,MD'与AD交于点G,则△AMG的内切圆半径的长为_____.
14.(本题4分)如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为______.
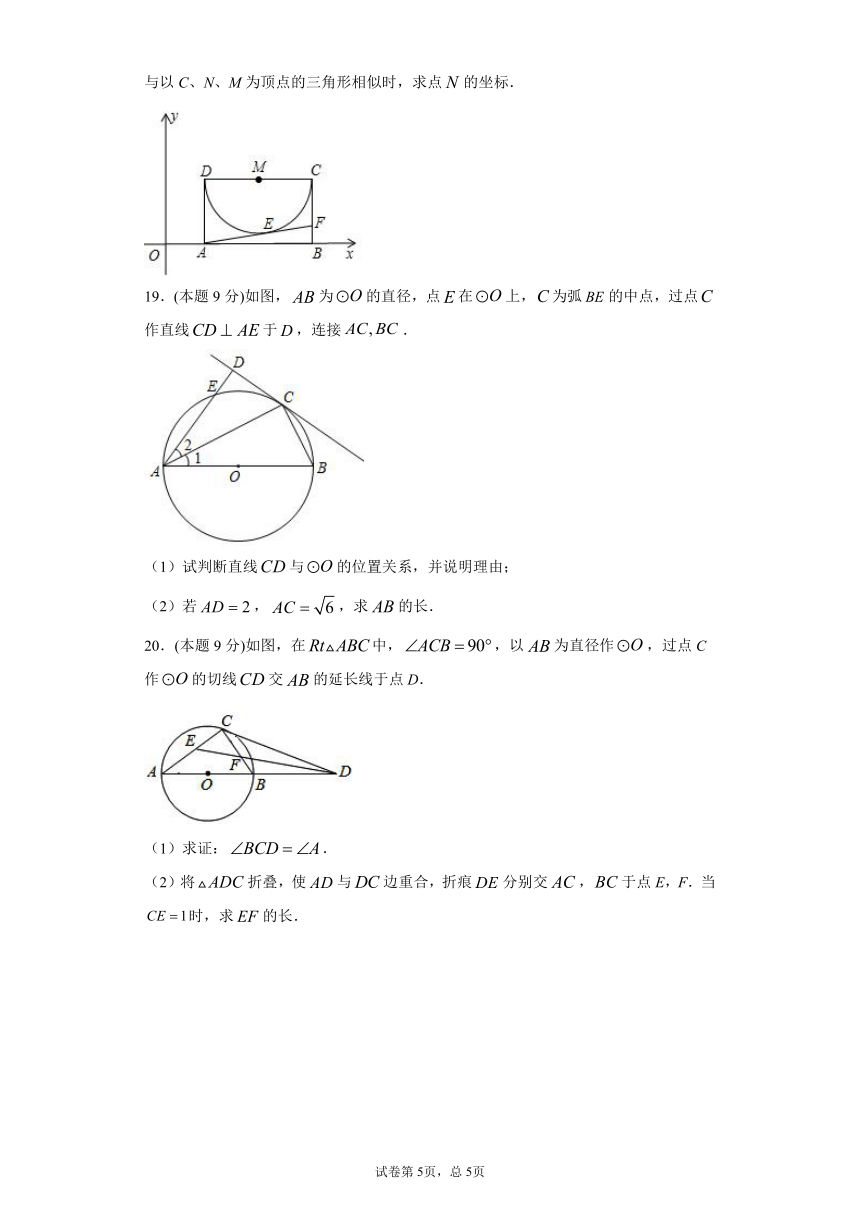
15.(本题4分)如图,∠ABC=80°,O为射线BC上一点,以点O为圆心、长为半径作☉O,要使射线BA与☉O相切,应将射线BA绕点B按顺时针方向旋转的度数为____.
16.(本题4分)如图,中,是线段上的一个动点,以为直径画分别交于,连接,则线段长度的最小值为_________.
三、解答题(共36分)
17.(本题9分)如图,已知是的直径,切于点C,交于点D,E为的中点,连接,.
(1)求证:是的切线;
(2)若,,求的长.
18.(本题9分)如图,在矩形ABCD中,AB=3,BC=2,点A的坐标为(1,0),以CD为直径,在矩形ABCD内作半圆,点M为圆心.设过A、B两点抛物线的解析式为y=ax2+bx+c,顶点为点N.
(1)求过A、C两点直线的解析式;
(2)当点N在半圆M内时,求a的取值范围;
(3)过点A作⊙M的切线交BC于点F,E为切点,当以点A、F,B为顶点的三角形与以C、N、M为顶点的三角形相似时,求点的坐标.
19.(本题9分)如图,为的直径,点在上,为弧的中点,过点作直线于,连接.
(1)试判断直线与的位置关系,并说明理由;
(2)若,,求的长.
20.(本题9分)如图,在中,,以为直径作,过点C作的切线交的延长线于点D.
(1)求证:.
(2)将折叠,使与边重合,折痕分别交,于点E,F.当时,求的长.
参考答案
1.D
2.B
3.A
4.D
5.A
6.C
7.A
8.D
9.C
10.C
11.
12.
13.
14.3cm或5cm
15.或
16.2,
17.(1)证明见解析;(2)
【详解】
(1)证明:连接,如图,
∵是的直径,
∴,
∴,
∵为的中点,
∴,
∴,
∵ ,
∴,
∵切于点,
∴,
∴,
∴,
∴是的切线;
(2)解:在中,
∵,,
∴
∵,,
∴,
∴,
即,
∴.
18.(1);(2);(3)
【详解】
(1)在矩形ABCD中,AB=3,BC=2,点A的坐标为(1,0),所以
设过A、C两点直线解析式为,则
解得 ,故过A、C两点直线解析式为;
(2)设过A、B两点抛物线的解析式为
整理得则顶点的坐标为 ,
由抛物线、半圆的轴对称可知,抛物线的顶点在过点且与垂直的直线上,又点在半圆内,
所以 解得;
(3)设,则,,,
在中,由勾股定理得,得
①由得,即
当点在的下方时,由,得
当点在的上方时,由,得
②由得,即
当点在的下方时,由,得
当点在的上方时,由,得
综上点的坐标为,,,.
19.(1)相切,证明见详解;(2)3
【详解】
证明:连接,
为的中点,
,
,
,
,
,
,
,
直线与相切;
(2)为直径,
,
,
,
,
,
,
.
20.(1)见解析;(2)
【详解】
解:(1)证明:如图,连接.
∵为的切线,
∴,
∴.
∵为的直径,
∴,即.
又∵,
∴,
∴.
(2)∵将折叠,使与边重合,
∴.
又∵,
∴,即,
∴.
∵,
∴,
∴.
一、单选题(共40分)
1.(本题4分)如图,是的直径,切于点T.若,则的度数为( )
A.52° B.54° C.56° D.76°
2.(本题4分)如图,中,,,,以斜边上的一点为圆心所作的半圆分别与相切于点,则为( )
A.2.5 B.1.6 C.1.5 D.2.6
3.(本题4分)如图,中,,,,以点为圆心,为半径作,当时,与的位置关系是( )
A.相切 B.相离 C.相交 D.无法确定
4.(本题4分)如图,分别切与点A,B,切于点C,分别交于点M,N,若,则的周长是( )
A. B. C. D.
5.(本题4分)中,斜边,其重心与外心之间的距离为( )
A.2 B.3 C.4 D.6
6.(本题4分)如图.PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OB,OP,AB.若 OA=1,∠APB=60°,则△PAB 的周长为( )
A.2 B.4 C.3 D.2+2
7.(本题4分)若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为,则实数a的值为( )
A.0或4 B.0或3
C.-2或6 D.-1或
8.(本题4分)如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )
A.35° B.45° C.65° D.70°
9.(本题4分)如图,菱形OABC的顶点A,B,C在上,过点B作的切线交OA的延长线于点D,若的半径为1,则BD的长为( )
A.1 B. C. D.2
10.(本题4分)如图,P是⊙O外一点,射线PA、PB分别切⊙O于点A、点B,CD切⊙O于点E,分别交PA、PB于点D、点C,若PB=4,则△PCD的周长( )
A.4 B.6 C.8 D.10
二、填空题(共24分)
11.(本题4分)在矩形中,,,点在对角线上,圆的半径为2,如果圆与矩形的各边都没有公共点,那么线段长的取值范围是______.
12.(本题4分)如图,为的割线,且,交于点C,若,则的半径的长为________.
13.(本题4分)如图,将边长为8的正方形纸片ABCD沿着EF折叠,使点C落在AB边的中点M处.点D落在点D'处,MD'与AD交于点G,则△AMG的内切圆半径的长为_____.
14.(本题4分)如图,直线a⊥b,垂足为H,点P在直线b上,PH=4cm,O为直线b上一动点,若以1cm为半径的⊙O与直线a相切,则OP的长为______.
15.(本题4分)如图,∠ABC=80°,O为射线BC上一点,以点O为圆心、长为半径作☉O,要使射线BA与☉O相切,应将射线BA绕点B按顺时针方向旋转的度数为____.
16.(本题4分)如图,中,是线段上的一个动点,以为直径画分别交于,连接,则线段长度的最小值为_________.
三、解答题(共36分)
17.(本题9分)如图,已知是的直径,切于点C,交于点D,E为的中点,连接,.
(1)求证:是的切线;
(2)若,,求的长.
18.(本题9分)如图,在矩形ABCD中,AB=3,BC=2,点A的坐标为(1,0),以CD为直径,在矩形ABCD内作半圆,点M为圆心.设过A、B两点抛物线的解析式为y=ax2+bx+c,顶点为点N.
(1)求过A、C两点直线的解析式;
(2)当点N在半圆M内时,求a的取值范围;
(3)过点A作⊙M的切线交BC于点F,E为切点,当以点A、F,B为顶点的三角形与以C、N、M为顶点的三角形相似时,求点的坐标.
19.(本题9分)如图,为的直径,点在上,为弧的中点,过点作直线于,连接.
(1)试判断直线与的位置关系,并说明理由;
(2)若,,求的长.
20.(本题9分)如图,在中,,以为直径作,过点C作的切线交的延长线于点D.
(1)求证:.
(2)将折叠,使与边重合,折痕分别交,于点E,F.当时,求的长.
参考答案
1.D
2.B
3.A
4.D
5.A
6.C
7.A
8.D
9.C
10.C
11.
12.
13.
14.3cm或5cm
15.或
16.2,
17.(1)证明见解析;(2)
【详解】
(1)证明:连接,如图,
∵是的直径,
∴,
∴,
∵为的中点,
∴,
∴,
∵ ,
∴,
∵切于点,
∴,
∴,
∴,
∴是的切线;
(2)解:在中,
∵,,
∴
∵,,
∴,
∴,
即,
∴.
18.(1);(2);(3)
【详解】
(1)在矩形ABCD中,AB=3,BC=2,点A的坐标为(1,0),所以
设过A、C两点直线解析式为,则
解得 ,故过A、C两点直线解析式为;
(2)设过A、B两点抛物线的解析式为
整理得则顶点的坐标为 ,
由抛物线、半圆的轴对称可知,抛物线的顶点在过点且与垂直的直线上,又点在半圆内,
所以 解得;
(3)设,则,,,
在中,由勾股定理得,得
①由得,即
当点在的下方时,由,得
当点在的上方时,由,得
②由得,即
当点在的下方时,由,得
当点在的上方时,由,得
综上点的坐标为,,,.
19.(1)相切,证明见详解;(2)3
【详解】
证明:连接,
为的中点,
,
,
,
,
,
,
,
直线与相切;
(2)为直径,
,
,
,
,
,
,
.
20.(1)见解析;(2)
【详解】
解:(1)证明:如图,连接.
∵为的切线,
∴,
∴.
∵为的直径,
∴,即.
又∵,
∴,
∴.
(2)∵将折叠,使与边重合,
∴.
又∵,
∴,即,
∴.
∵,
∴,
∴.
