2020-2021学年 浙教版 八年级数学下册 第2章 一元二次方程 2.3~2.4 综合提高卷(Word版 含答案)
文档属性
| 名称 | 2020-2021学年 浙教版 八年级数学下册 第2章 一元二次方程 2.3~2.4 综合提高卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 403.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-29 10:43:19 | ||
图片预览


文档简介
2020-2021学年浙教版八年级数学下册第二章《一元二次方程》2.3~2.4综合提高卷
班级
姓名
学号
一、选择题(每题3分,共30分)
1.已知x1,x2是一元二次方程x2
-
2x
=
0的两根,则x1
+x2的值是(
)
A.0
B.2
C.
-
2
D.4
2.下列一元二次方程中,两实数根的和为
-
4的是(
)
A.x2
+
2x
-
4
=
0
B.x2
-
4x
+
4
=
0
C.x2
+
4x
+
10
=
0
D.x2
+
4x
-
5
=
0
3.某地区居民2017年人均收入12000元,预计2019年人均收入将达到60000元,设2017年到2019年该地区居民年人均收入平均增长率为x,可列方程为(
)
A.12000(1
+
2x)
=
60000
B.12000(1+x)2
=
60000
C.12000(1
+
x2)
=
60000
D.12000
+
2x
=
60000
4.若一元二次方程x2
+
x
-
1
=
0的较大根是m,则(
)
A.m
>
2
B.m
<-
1
C.1
<
m
<
2
D.0
<
m
<
1
5.若关于x的方程x2
+
2x
-
a
=
0有两个相等的实数根,则a的值为(
)
A.
-
1
B.1
C.-
4
D.4
6.某服装店从6月份开始对春装进行“折上折”(两次打折数相同)优惠活动.已知一件原价500元的春装,优惠后实际仅需320元,设该店春装原本打x折,则有(
)
A.500(1
-
2x)
=
320
B.500(1-x)2
=
320
C.500=
320
D.500
=
320
7.某单位要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,则参加比赛的球队应有(
)
A.7队
B.6队
C.5队
D.4队
8.某种植物的主干长出若干个支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是111,求每个支干长出多少个小分支.设主干长出x个支干,每个支干长出x个小分支,由题意,所列方程正确的是(
)
A.1
+
x
+
x2
=
111
B.x
+
x2
=
111
C.2x
+
1
=
111
D.2x
=
111
9.如图所示,在△ABC中,AC
=
50
m,BC
=
40
m,∠C
=
90°,点P从点A开始沿射线AC方向以2
m/s的速度匀速移动,同时另一点Q由点C开始以3
m/s的速度沿射线CB方向匀速移动,当△PCQ的面积等于300
m2时,运动时间为(
)
A.5s
B.20s
C.5s或20s
D.6s或18s
10.对于方程x2
-
2|x|
=
m,若方程实数根的个数为4,则m的值可能等于(
)
A.
-
1
B.1
C.0
D.
-
二、填空题(每题4分,共24分)
11.若x1,x2是一元二次方程x2
-
6x
-
2
=
0的两个实数根,则x1+x2
=
_________
.
12.如图所示,某居民小区要在一块一边靠墙的空地上建一个长方形花园ABCD,花园的中间用平行于AB的栅栏EF隔开,花园一边靠墙,其余部分用总长为30
m的栅栏围成且面积刚好等于72
m2,求围成花园的宽AB为多少米.设AB
=
x(m),由题意可列方程为
_________
.
13.定义[a,b]为一次函数y
=
ax
+
b(a≠0,a,b为实数)的“关联数”,若“关联数”为[1,m
-
2]的一次函数是正比例函数,则关于x的方程x2
+
3x
+
m
=
0的解为
_________
.
14.某大学土木工程专业2017年毕业500名大学生,2019年毕业605名大学生.若该大学土木工程专业毕业大学生的年平均增长率相同,则该大学土木工程专业2018年毕业的大学生有
_________
名.
15.已知a为实数,且满足(a2+b2)2
+
2(a2
+
b2)-
15
=
0,则代数式a2
+
b2的值为
_________
.
16.某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元.为了扩大销售量,增加盈利,该商场采取了降价措施,经调查发现如果每件衬衫降价1元,那么商场平均每天可多售出2件衬衫.若商场平均每天要盈利1200元,则每件衬衫应降价
_________
.
三、解答题(共66分)
17.(6分)如图所示为某个月的月历,在此月历上用一个长方形任意圈出2
×
2个数(如17,18,24,25),如果圈出的四个数中最小数与最大数的积为153,求这四个数的和.
18.(8分)设a,b是方程x2
+
x
-2018
=
0的两个不相等的实数根.
(1)a
+
b
=
_________
;ab
=
_________
.
(2)求代数式a2
+
2a
+
b的值.
19.(8分)关于x的一元二次方程x2
+
3x
+
m
-
1
=
0的两个实数根分别为x1,x2
(1)求m的取值范围.
(2)若2(x1+x2)
+
x1x2
+
10
=
0,求m的值.
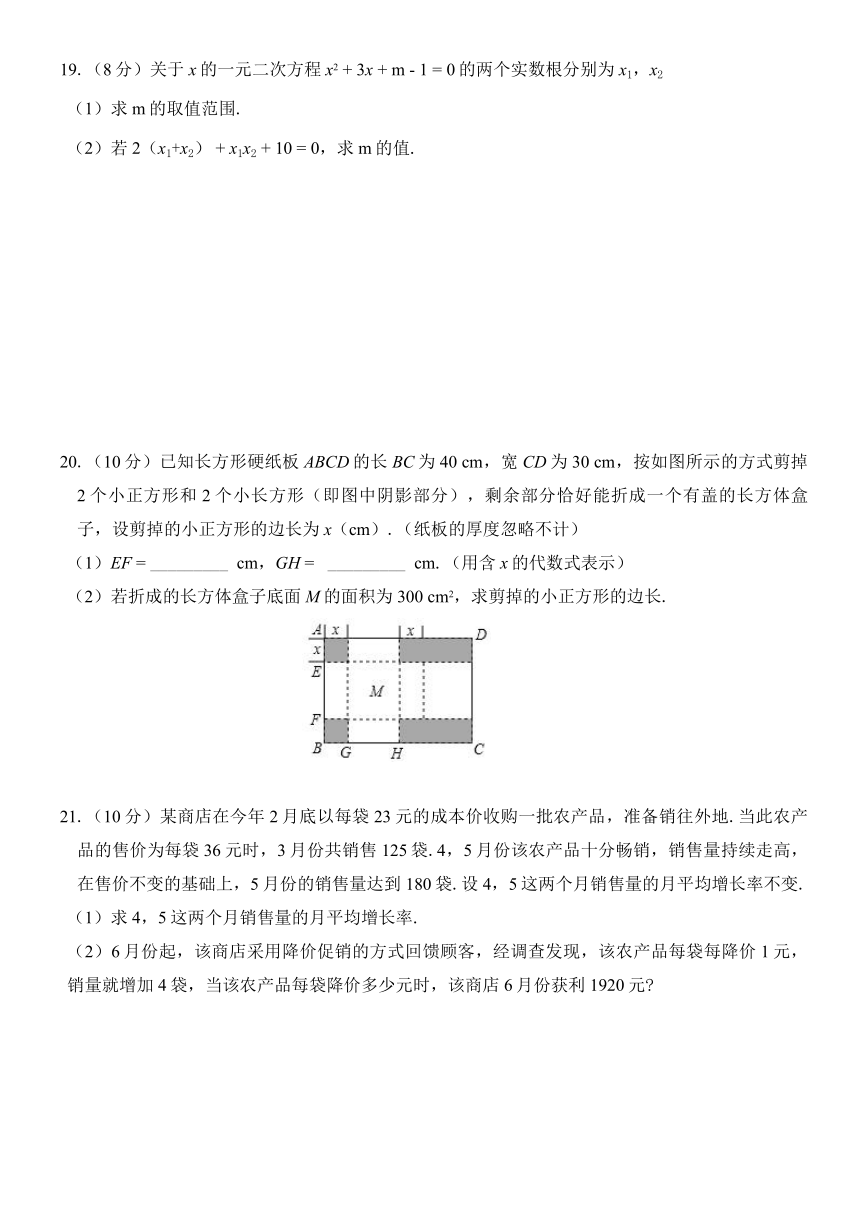
20.(10分)已知长方形硬纸板ABCD的长BC为40
cm,宽CD为30
cm,按如图所示的方式剪掉2个小正方形和2个小长方形(即图中阴影部分),剩余部分恰好能折成一个有盖的长方体盒子,设剪掉的小正方形的边长为x(cm).(纸板的厚度忽略不计)
(1)EF
=
_________
cm,GH
=
_________
cm.(用含x的代数式表示)
(2)若折成的长方体盒子底面M的面积为300
cm2,求剪掉的小正方形的边长.
21.(10分)某商店在今年2月底以每袋23元的成本价收购一批农产品,准备销往外地.当此农产品的售价为每袋36元时,3月份共销售125袋.4,5月份该农产品十分畅销,销售量持续走高,在售价不变的基础上,5月份的销售量达到180袋.设4,5这两个月销售量的月平均增长率不变.
(1)求4,5这两个月销售量的月平均增长率.
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每袋每降价1元,销量就增加4袋,当该农产品每袋降价多少元时,该商店6月份获利1920元?
22.(12分)已知关于x的方程x2
-(2k
+
1)x
+
4(k
-
)
=
0.
(1)求证:无论k取什么实数值,这个方程总有实数根.
(2)能否找到一个实数k,使方程的两实数根互为相反数?若能找到,求出k的值;若不能,请说明理由.
(3)若等腰三角形ABC的一边长a
=
4,另两边的长b,c恰好是这个方程的两根,求△ABC的周长.
23.(12分)某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.修建每公顷大棚平均要用的支架、塑料膜等材料的费用为27000元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为9000.每公顷大棚的年平均经济收益为75000元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为60000元.
(1)一年中这个村修建了多少公顷蔬菜大棚?
(2)一年中修建2公顷大棚与修建公顷大棚的收益有什么差别?
(3)如果修建3公顷大棚,那么收益如何?
(4)修建大棚的面积越大收益也一定越大吗?
_________
(填“一定”或“不一定”)
24.(12分)如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2
24.
班级
姓名
学号
一、选择题(每题3分,共30分)
1.已知x1,x2是一元二次方程x2
-
2x
=
0的两根,则x1
+x2的值是(
)
A.0
B.2
C.
-
2
D.4
2.下列一元二次方程中,两实数根的和为
-
4的是(
)
A.x2
+
2x
-
4
=
0
B.x2
-
4x
+
4
=
0
C.x2
+
4x
+
10
=
0
D.x2
+
4x
-
5
=
0
3.某地区居民2017年人均收入12000元,预计2019年人均收入将达到60000元,设2017年到2019年该地区居民年人均收入平均增长率为x,可列方程为(
)
A.12000(1
+
2x)
=
60000
B.12000(1+x)2
=
60000
C.12000(1
+
x2)
=
60000
D.12000
+
2x
=
60000
4.若一元二次方程x2
+
x
-
1
=
0的较大根是m,则(
)
A.m
>
2
B.m
<-
1
C.1
<
m
<
2
D.0
<
m
<
1
5.若关于x的方程x2
+
2x
-
a
=
0有两个相等的实数根,则a的值为(
)
A.
-
1
B.1
C.-
4
D.4
6.某服装店从6月份开始对春装进行“折上折”(两次打折数相同)优惠活动.已知一件原价500元的春装,优惠后实际仅需320元,设该店春装原本打x折,则有(
)
A.500(1
-
2x)
=
320
B.500(1-x)2
=
320
C.500=
320
D.500
=
320
7.某单位要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,则参加比赛的球队应有(
)
A.7队
B.6队
C.5队
D.4队
8.某种植物的主干长出若干个支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是111,求每个支干长出多少个小分支.设主干长出x个支干,每个支干长出x个小分支,由题意,所列方程正确的是(
)
A.1
+
x
+
x2
=
111
B.x
+
x2
=
111
C.2x
+
1
=
111
D.2x
=
111
9.如图所示,在△ABC中,AC
=
50
m,BC
=
40
m,∠C
=
90°,点P从点A开始沿射线AC方向以2
m/s的速度匀速移动,同时另一点Q由点C开始以3
m/s的速度沿射线CB方向匀速移动,当△PCQ的面积等于300
m2时,运动时间为(
)
A.5s
B.20s
C.5s或20s
D.6s或18s
10.对于方程x2
-
2|x|
=
m,若方程实数根的个数为4,则m的值可能等于(
)
A.
-
1
B.1
C.0
D.
-
二、填空题(每题4分,共24分)
11.若x1,x2是一元二次方程x2
-
6x
-
2
=
0的两个实数根,则x1+x2
=
_________
.
12.如图所示,某居民小区要在一块一边靠墙的空地上建一个长方形花园ABCD,花园的中间用平行于AB的栅栏EF隔开,花园一边靠墙,其余部分用总长为30
m的栅栏围成且面积刚好等于72
m2,求围成花园的宽AB为多少米.设AB
=
x(m),由题意可列方程为
_________
.
13.定义[a,b]为一次函数y
=
ax
+
b(a≠0,a,b为实数)的“关联数”,若“关联数”为[1,m
-
2]的一次函数是正比例函数,则关于x的方程x2
+
3x
+
m
=
0的解为
_________
.
14.某大学土木工程专业2017年毕业500名大学生,2019年毕业605名大学生.若该大学土木工程专业毕业大学生的年平均增长率相同,则该大学土木工程专业2018年毕业的大学生有
_________
名.
15.已知a为实数,且满足(a2+b2)2
+
2(a2
+
b2)-
15
=
0,则代数式a2
+
b2的值为
_________
.
16.某商场销售一批名牌衬衫,平均每天可售出20件,每件可盈利40元.为了扩大销售量,增加盈利,该商场采取了降价措施,经调查发现如果每件衬衫降价1元,那么商场平均每天可多售出2件衬衫.若商场平均每天要盈利1200元,则每件衬衫应降价
_________
.
三、解答题(共66分)
17.(6分)如图所示为某个月的月历,在此月历上用一个长方形任意圈出2
×
2个数(如17,18,24,25),如果圈出的四个数中最小数与最大数的积为153,求这四个数的和.
18.(8分)设a,b是方程x2
+
x
-2018
=
0的两个不相等的实数根.
(1)a
+
b
=
_________
;ab
=
_________
.
(2)求代数式a2
+
2a
+
b的值.
19.(8分)关于x的一元二次方程x2
+
3x
+
m
-
1
=
0的两个实数根分别为x1,x2
(1)求m的取值范围.
(2)若2(x1+x2)
+
x1x2
+
10
=
0,求m的值.
20.(10分)已知长方形硬纸板ABCD的长BC为40
cm,宽CD为30
cm,按如图所示的方式剪掉2个小正方形和2个小长方形(即图中阴影部分),剩余部分恰好能折成一个有盖的长方体盒子,设剪掉的小正方形的边长为x(cm).(纸板的厚度忽略不计)
(1)EF
=
_________
cm,GH
=
_________
cm.(用含x的代数式表示)
(2)若折成的长方体盒子底面M的面积为300
cm2,求剪掉的小正方形的边长.
21.(10分)某商店在今年2月底以每袋23元的成本价收购一批农产品,准备销往外地.当此农产品的售价为每袋36元时,3月份共销售125袋.4,5月份该农产品十分畅销,销售量持续走高,在售价不变的基础上,5月份的销售量达到180袋.设4,5这两个月销售量的月平均增长率不变.
(1)求4,5这两个月销售量的月平均增长率.
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每袋每降价1元,销量就增加4袋,当该农产品每袋降价多少元时,该商店6月份获利1920元?
22.(12分)已知关于x的方程x2
-(2k
+
1)x
+
4(k
-
)
=
0.
(1)求证:无论k取什么实数值,这个方程总有实数根.
(2)能否找到一个实数k,使方程的两实数根互为相反数?若能找到,求出k的值;若不能,请说明理由.
(3)若等腰三角形ABC的一边长a
=
4,另两边的长b,c恰好是这个方程的两根,求△ABC的周长.
23.(12分)某村为增加蔬菜的种植面积,一年中修建了一些蔬菜大棚.修建每公顷大棚平均要用的支架、塑料膜等材料的费用为27000元,此外还要购置喷灌设备,这项费用(元)与大棚面积(公顷)的平方成正比,比例系数为9000.每公顷大棚的年平均经济收益为75000元,这个村一年中由于修建蔬菜大棚而增加的收益(扣除修建费用后)为60000元.
(1)一年中这个村修建了多少公顷蔬菜大棚?
(2)一年中修建2公顷大棚与修建公顷大棚的收益有什么差别?
(3)如果修建3公顷大棚,那么收益如何?
(4)修建大棚的面积越大收益也一定越大吗?
_________
(填“一定”或“不一定”)
24.(12分)如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2
24.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
