3.4.2圆柱 同步练习(含解析)
图片预览


文档简介
初中数学浙教版九年级下册3.4.2圆柱 同步练习
一、单选题
1.一个立体图形的三视图如图所示.根据图中数据求得这个立体图形的表面积为(?? )
A.?2π????????????????????????????????????????B.?6π????????????????????????????????????????C.?7π????????????????????????????????????????D.?8π
2.乐乐玩橡皮泥时,将一个底面直径为4cm,高为4cm的圆柱,捏成底面直径为3.2cm的圆柱,则圆柱的高变成了(?? )
A.?7.5cm?????????????????????????????????B.?6.25cm?????????????????????????????????C.?5cm?????????????????????????????????D.?4.75cm
3.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是(?? )
A.?30cm2??????????????????????????????B.?30πcm2??????????????????????????????C.?15cm2??????????????????????????????D.?15πcm2
4.一个长方形长为4cm,宽为2cm,以它的长边为轴,把长方形转一周后,得到一个圆柱体体积为(?? )
A.?8πcm3??????????????????????????????B.?4πcm3??????????????????????????????C.?16πcm3??????????????????????????????D.?12πcm3
5.一个圆柱的高是10分米,底面积为6.28平方分米,把它截成两个同样的小圆柱后,表面积比原来增加了(?? )平方分米.
A.?6.28?????????????????????????????????????B.?9.42?????????????????????????????????????C.?10?????????????????????????????????????D.?12.56
6.矩形ABCD中,AB=3,BC=4,以AB为轴旋转一周得到圆柱,则它的表面积是(?? )
A.?60π?????????????????????????????????????B.?56π?????????????????????????????????????C.?32π?????????????????????????????????????D.?24π
7.已知圆柱的母线长5,侧面积为30π,则圆柱的底面直径长是( )
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
8.底面半径R,高为h的圆柱与底面半径为r,高为h的圆柱的体积的比是9:25,则R:r等于( )A.?9:25???????????????????????????????????B.?25:9???????????????????????????????????C.?3:5???????????????????????????????????D.?5:3
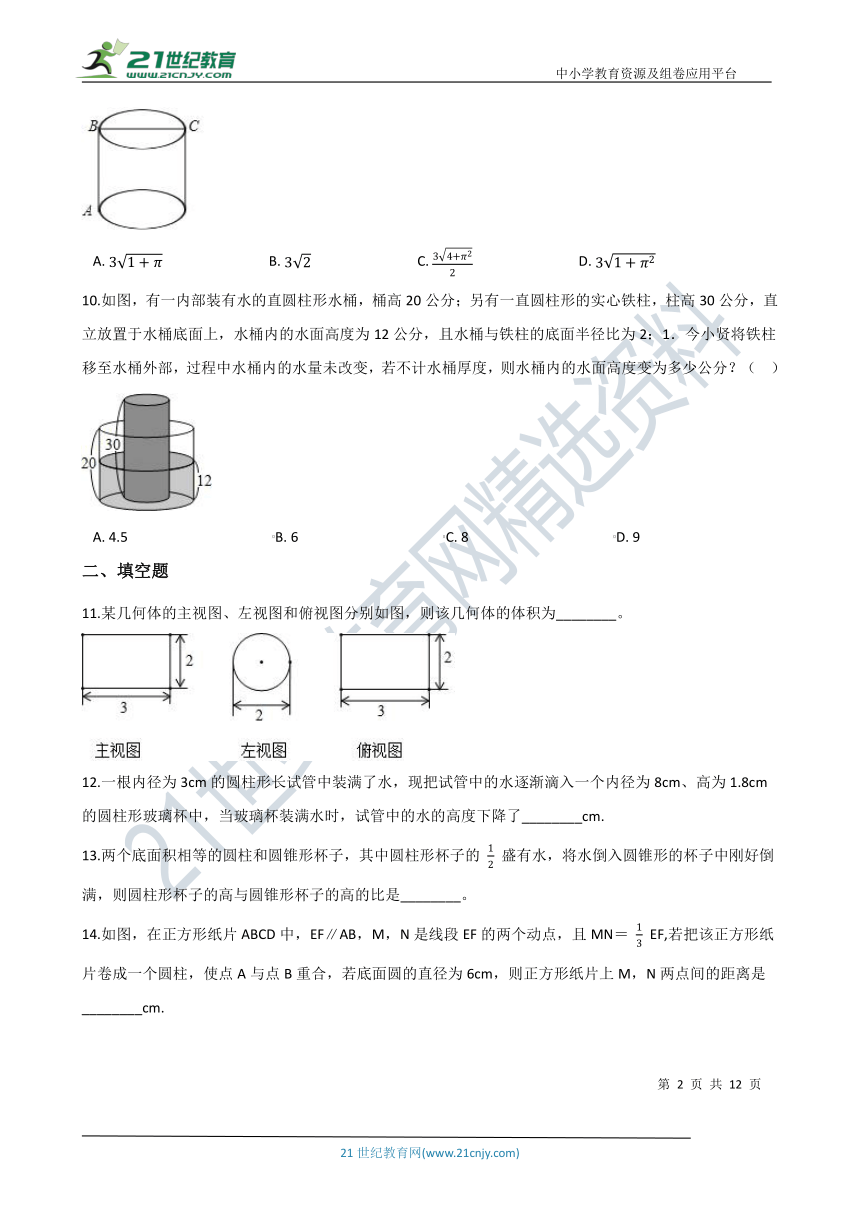
9.如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是(?? )
A.?31+π???????????????????????????????B.?32???????????????????????????????C.?34+π22???????????????????????????????D.?31+π2
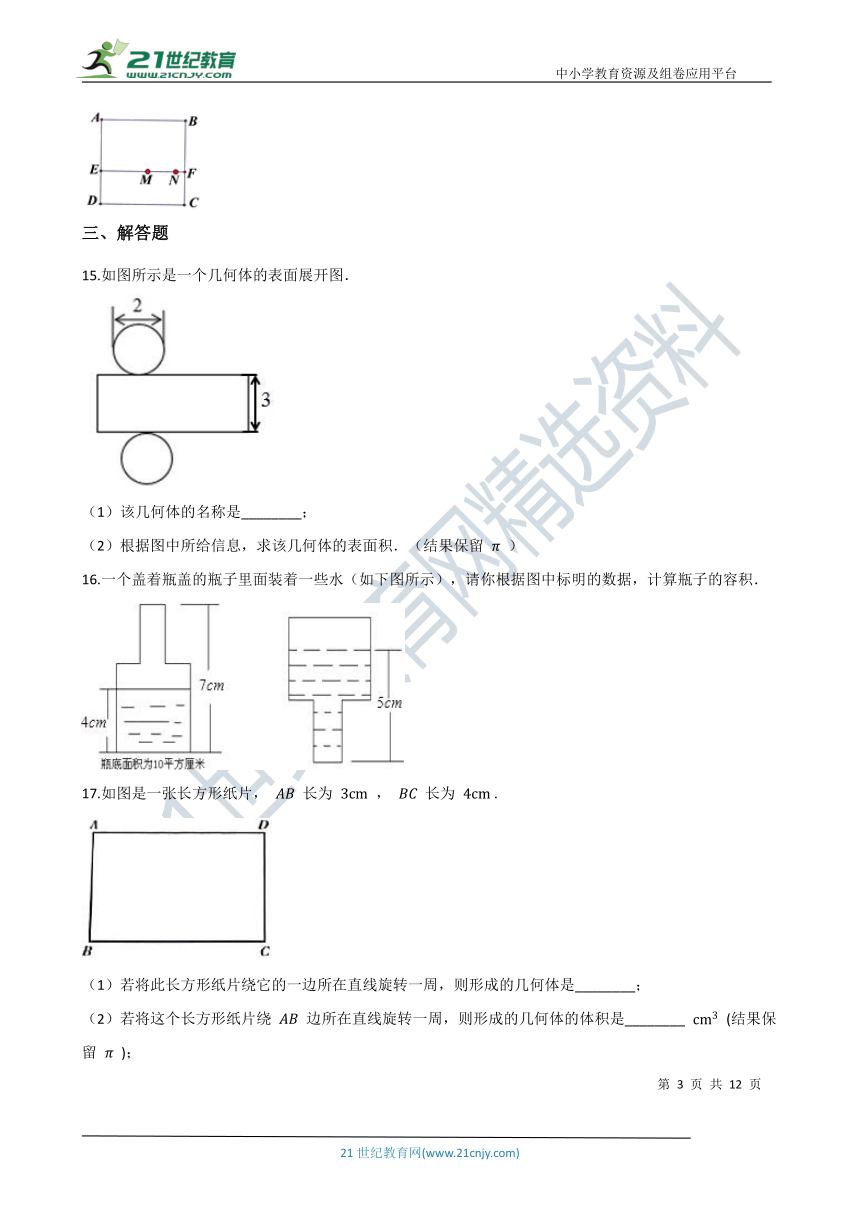
10.如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?(?? )
A.?4.5??????????????????????????????????????????B.?6??????????????????????????????????????????C.?8??????????????????????????????????????????D.?9
二、填空题
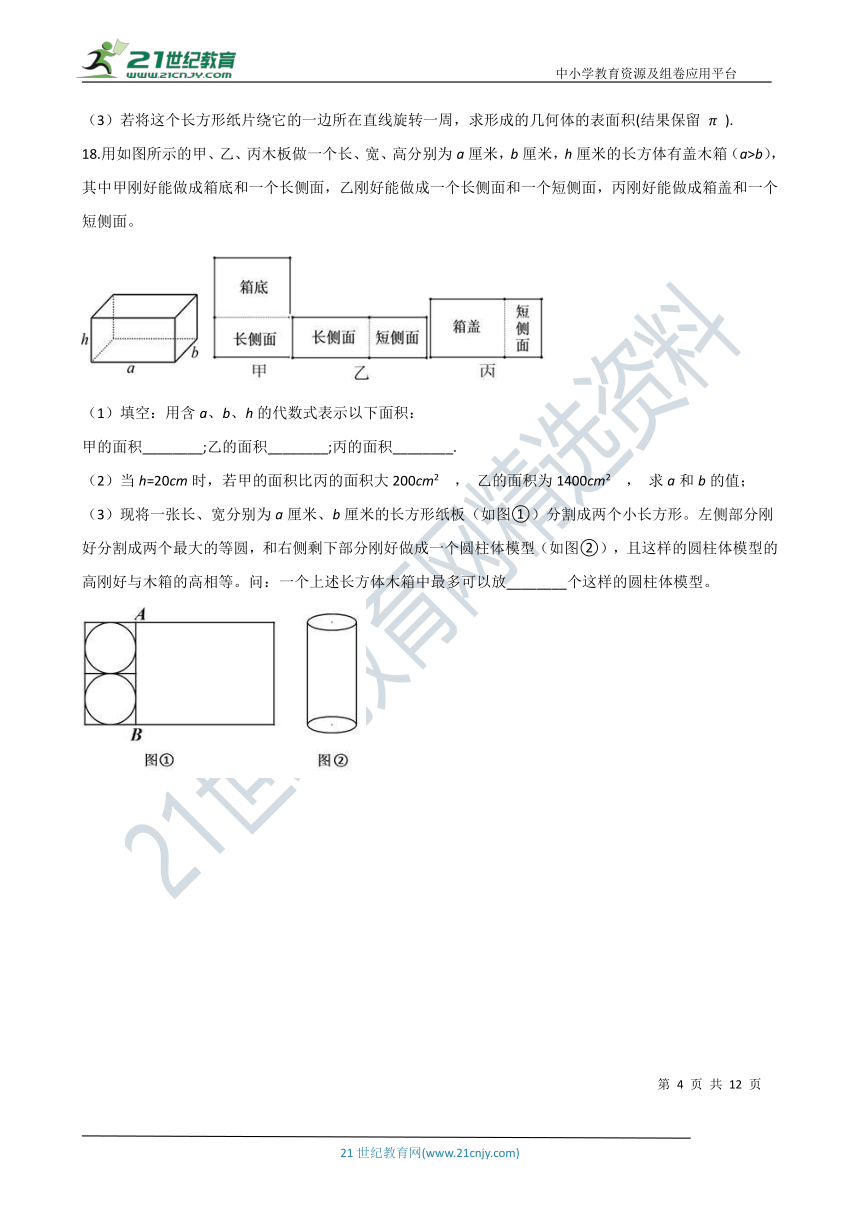
11.某几何体的主视图、左视图和俯视图分别如图,则该几何体的体积为________。
12.一根内径为3cm的圆柱形长试管中装满了水,现把试管中的水逐渐滴入一个内径为8cm、高为1.8cm的圆柱形玻璃杯中,当玻璃杯装满水时,试管中的水的高度下降了________cm.
13.两个底面积相等的圆柱和圆锥形杯子,其中圆柱形杯子的 12 盛有水,将水倒入圆锥形的杯子中刚好倒满,则圆柱形杯子的高与圆锥形杯子的高的比是________。
14.如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN= 13 EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是________cm.
三、解答题
15.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是________;
(2)根据图中所给信息,求该几何体的表面积.(结果保留 π )
16.一个盖着瓶盖的瓶子里面装着一些水(如下图所示),请你根据图中标明的数据,计算瓶子的容积.
17.如图是一张长方形纸片, AB 长为 3cm , BC 长为 4cm .
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是________;
(2)若将这个长方形纸片绕 AB 边所在直线旋转一周,则形成的几何体的体积是________ cm3 (结果保留 π );
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留 π ).
18.用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。
(1)填空:用含a、b、h的代数式表示以下面积:
甲的面积________;乙的面积________;丙的面积________.
(2)当h=20cm时,若甲的面积比丙的面积大200cm2 , 乙的面积为1400cm2 , 求a和b的值;
(3)现将一张长、宽分别为a厘米、b厘米的长方形纸板(如图①)分割成两个小长方形。左侧部分刚好分割成两个最大的等圆,和右侧剩下部分刚好做成一个圆柱体模型(如图②),且这样的圆柱体模型的高刚好与木箱的高相等。问:一个上述长方体木箱中最多可以放________个这样的圆柱体模型。
答案解析部分
一、单选题
1. D
考点:圆柱的计算,由三视图判断几何体
解:∵正视图和俯视图是矩形,左视图为圆形,
∴可得这个立体图形是圆柱,
∴这个立体图形的侧面积是2π×3=6π,
底面积是:π?12=π,
∴这个立体图形的表面积为6π+2π=8π;
故答案为:D.
分析:从三视图可知正视图以及俯视图为矩形,而左视图为圆形,可以得出该立体图形为圆柱,再由三视图可知圆柱底面圆的半径和高,求出表面积即可.
2. B
考点:圆柱的计算
解:设高变成了xcm,根据题意得
π×(4÷2)2×4=π×(3.2÷2)2×x,
解得x=6.25,
答:高变成了6.25cm.
故答案为:B.
分析:设高变成了xcm,根据圆柱的体积保持不变列出方程求解即可
3. B
考点:几何体的表面积,圆柱的计算
解:根据圆柱的侧面积公式,可得该圆柱的侧面积为:2π×3×5=30πcm2 .
故选B.
分析:圆柱侧面积=底面周长×高.
4.C
考点:圆柱的计算
解:根据圆柱体的体积计算公式,体积=πr2×高=4π×4=16πcm3 . 故选C. 分析:根据面动成体的原理可知旋转后的圆柱体的半径为2cm,根据圆柱体的面积计算公式即可解.
5. D
考点:圆柱的计算
解:由题意可得,
把原来的圆柱截成两个同样的小圆柱后,增加了两个圆面,
故表面积比原来增加了6.28×2=12.56(平方分米),
故选D.
分析:根据题意可知,把原来的圆柱截成两个同样的小圆柱后,增加了两个圆面,从而可以解答本题.
6. B
考点:点、线、面、体及之间的联系,圆柱的计算
解:∵以直线AB为轴旋转一周得到的圆柱体,得出底面半径为4cm,母线长为3cm,
∴圆柱侧面积=2π?AB?BC=2π?3×4=24π(cm2),
∴底面积=π?BC2=π?42=16π(cm2),
∴圆柱的表面积=24π+2×16π=56π(cm2).
故选B.
分析:表面积=侧面积+两个底面积=底面周长×高+2πr2 .
7. B
考点:圆柱的计算
解:∵圆柱的母线长5,侧面积为30π,
∴底面周长为:30π÷5=6π,
则圆柱的底面直径长是:6π÷π=6.
故选:B.
分析:利用圆柱侧面积计算公式,进而求出底面圆的周长,进而得出答案.
8. C
考点:圆柱的计算
解:根据圆柱体积的计算方法和积的变化规律,再根据圆的面积与半径的关系,已知两个圆柱的高相等,两个圆柱体积的比是9:25,所以两个圆柱底面半径的比是3:5.
故选:C.
分析:根据圆柱的体积公式:v=sh,和圆的面积公式:s=πr2 , 圆的面积扩大的倍数等于半径扩大倍数的平方.已知两个圆柱的高相等,两个圆柱体积的比是9:25,所以两个圆柱底面半径的比是3:5.由此解答.
9. C
考点:圆柱的计算
解:把圆柱侧面展开,展开图如图所示,点A、C的最短距离为线段AC的长.
在Rt△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=1.5π,
所以AC= 32+(32π)2=34+π2 ,
故答案为:C.
分析:要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.
10. D
考点:圆柱的计算
解:∵水桶底面半径:铁柱底面半径=2:1,
∴水桶底面积:铁柱底面积=22:12=4:1,
设铁柱底面积为a,水桶底面积为4a,
则水桶底面扣除铁柱部分的环形区域面积为4a﹣a=3a,
∵原有的水量为3a×12=36a,
∴水桶内的水面高度变为 36a4a ?=9(公分).
故选D.
分析:由水桶底面半径:铁柱底面半径=2:1,得到水桶底面积:铁柱底面积=22:12=4:1,设铁柱底面积为a,水桶底面积为4a,于是得到水桶底面扣除铁柱部分的环形区域面积为4a﹣a=3a,根据原有的水量为3a×12=36a,即可得到结论.
二、填空题
11. 3π
考点:圆柱的计算
解:根据三视图可以判断该几何体为圆柱,圆柱的底面半径为1,高为3,
故体积为: πr2h=π×1×3=3π ,
故答案为: 3π .
分析:根据三视图可以判断该几何体为倒放的圆柱,圆柱的底面半径为1,高为3,据此求得其体积即可.
12. 12.8
考点:圆柱的计算,关于圆柱的应用题
解:设试管中的水的高度下降了xcm;
根据题意有: π×1.52×x=π×(82)2×1.8 ;
解之得:x=12.8.
故答案为12.8.
分析:根据题意可知,内径为3cm的圆柱形长试管中水柱少的体积等于内径为8cm、高为1.8cm的圆柱形玻璃杯的体积,用此作为相等关系列方程求解。
13. 2:3
考点:圆锥的计算,圆柱的计算
解: 解:设圆柱和圆锥形杯子的底面积为s,圆柱的高为h1 , 圆锥的高为h2 ,
根据题意得:2×13sh2=sh1 ,
∴h1∶h2=2∶3 ,
∴ 圆柱形杯子的高与圆锥形杯子的高的比是2:3.
故答案为:2:3.
分析:设圆柱和圆锥形杯子的底面积为s,圆柱的高为h1 , 圆锥的高为h2 , 根据题意列出等式,求出h1∶h2=2∶3 , 即可求解.
14. 2π
考点:圆柱的计算
解:根据题意得:EF=AD=BC,MN=2EM= 13 EF,
∵把该正方形纸片卷成一个圆柱,使点A与点D重合,底面圆的直径为6cm,
∴底面周长为6πcm,即EF=6πcm,
则MN= 6π3=2π cm,
故答案为 6π3=2π .
分析:根据题意得到EF=AD=BC,MN=2EM,由卷成圆柱后底面直径求出周长,除以6得到EM的长,进而确定出MN的长即可.
三、解答题
15. (1)圆柱
(2)解:该几何体的的表面积=π×12×2+2π×3=8π.
考点:圆柱的计算,圆柱的展开图
解:(1)该几何体的名称是圆柱,
故答案为:圆柱
分析:(1)根据圆柱的特征求解;(2)先计算侧面,再计算底面,最后相加即可。
16. 解:由已知条件知,第二个图上部空白部分的高为7﹣5=2cm,
从而水与空着的部分的体积比为4:2=2:1.
由第一个图知水的体积为10×4=40,所以总的容积为40÷2×(2+1)=60立方厘米
考点:圆柱的计算
分析:结合图形,知水的体积不变,从而根据第二个图空着的部分的高度是2cm,可以求得水与空着的部分的体积比为4:2=2:1.结合第一个图中水的体积,即可求得总容积.
17. (1)圆柱
(2)48π
(3)解:绕 AB 边所在直线旋转得到的圆柱的底面半径为 4cm ,高为 3cm ,
表面积是: 2π×4×3+42×π=40π(cm2) ;
绕 AD 边所在直线旋转得到的圆柱的底面半径为 3cm ,高为 4cm ,
表面积是: 2π×4×3+32×π=33π(cm2) .
答:形成的几何体的表面积是 40πcm2 或 33πcm2
考点:圆柱的计算
解:(1)圆柱;(2) 绕AB旋转得到的圆柱的底面半径为 4cm ,高为 3cm ,体积 =π×42×3=48πcm3 ;
分析:(1)根据圆柱体的纵截面是长方形,因此长方形纸片绕它的一边所在直线旋转一周,所形成的几何体是圆柱。
(2)将这个长方形纸片绕AB边所在直线旋转一周,可知底面圆的半径为BC的长,母线长为AB的长,再根据圆柱的面积等于底面圆的面积×母线长,列式计算可求解。
(3)分两种情况:绕AB边所在直线旋转得到的圆柱; 绕 AD边所在直线旋转得到的圆柱,再根据圆柱的表面积=圆柱的侧面积+底面圆的面积,然后列式分别求解。
18. (1)ab+ah;ah+bh;ab+bh
(2)解: {(ab+20a)-(ab+20b)=20020a+20b=1400 ,
化简得 {a-b=10a+b=70 ,
解得: {a=40b=30 .
(3)8
考点:列式表示数量关系,矩形的性质,圆柱的计算,二元一次方程组的应用-几何问题
解:(1)甲的面积= ab+ah ,乙的面积= ah ?????+bh; 丙的面积 =ab+bh;
(3)设圆的直径为d,
∵将一张长、宽分别为a厘米、b厘米的长方形纸板(如图①)分割成两个小长方形。左侧部分刚好分割成两个最大的等圆,和右侧剩下部分刚好做成一个圆柱体模型,
∴b=2d,a-d=πd,
∴a=(π+1)d
∵圆柱体模型的高刚好与木箱的高相等,
∴只有比较木箱的上表面有几个正方形ACDF即可,
∴abd2=π+1d·2dd2=2π+1≈8.28
∴可以放两层,
∴b=2r+πr
∴b2r=πr+2r2r=π2+1≈2.57
∴一个上述长方体木箱中最多可以放8个这样的圆柱体模型.
故答案为:8.
分析:(1)根据矩形的面积公式,分别求出甲,乙,丙的面积即可;
(2)根据甲的面积-丙的面积=200cm2 , 乙的面积为1400cm2 , 列出方程组,将h=20cm代入并解出方程组,即可求出a,b的值;
(3)设圆的直径为d,观察图像由已知可得到b=2d,a=(π+1)d,再根据圆柱体模型的高刚好与木箱的高相等,就可得到只有比较木箱的上表面有几个正方形ACDF即可,因此利用木箱的上表面的面积除以正方形ACDF的面积即可求解。
一、单选题
1.一个立体图形的三视图如图所示.根据图中数据求得这个立体图形的表面积为(?? )
A.?2π????????????????????????????????????????B.?6π????????????????????????????????????????C.?7π????????????????????????????????????????D.?8π
2.乐乐玩橡皮泥时,将一个底面直径为4cm,高为4cm的圆柱,捏成底面直径为3.2cm的圆柱,则圆柱的高变成了(?? )
A.?7.5cm?????????????????????????????????B.?6.25cm?????????????????????????????????C.?5cm?????????????????????????????????D.?4.75cm
3.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是(?? )
A.?30cm2??????????????????????????????B.?30πcm2??????????????????????????????C.?15cm2??????????????????????????????D.?15πcm2
4.一个长方形长为4cm,宽为2cm,以它的长边为轴,把长方形转一周后,得到一个圆柱体体积为(?? )
A.?8πcm3??????????????????????????????B.?4πcm3??????????????????????????????C.?16πcm3??????????????????????????????D.?12πcm3
5.一个圆柱的高是10分米,底面积为6.28平方分米,把它截成两个同样的小圆柱后,表面积比原来增加了(?? )平方分米.
A.?6.28?????????????????????????????????????B.?9.42?????????????????????????????????????C.?10?????????????????????????????????????D.?12.56
6.矩形ABCD中,AB=3,BC=4,以AB为轴旋转一周得到圆柱,则它的表面积是(?? )
A.?60π?????????????????????????????????????B.?56π?????????????????????????????????????C.?32π?????????????????????????????????????D.?24π
7.已知圆柱的母线长5,侧面积为30π,则圆柱的底面直径长是( )
A.?3???????????????????????????????????????????B.?6???????????????????????????????????????????C.?9???????????????????????????????????????????D.?12
8.底面半径R,高为h的圆柱与底面半径为r,高为h的圆柱的体积的比是9:25,则R:r等于( )A.?9:25???????????????????????????????????B.?25:9???????????????????????????????????C.?3:5???????????????????????????????????D.?5:3
9.如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是(?? )
A.?31+π???????????????????????????????B.?32???????????????????????????????C.?34+π22???????????????????????????????D.?31+π2
10.如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?(?? )
A.?4.5??????????????????????????????????????????B.?6??????????????????????????????????????????C.?8??????????????????????????????????????????D.?9
二、填空题
11.某几何体的主视图、左视图和俯视图分别如图,则该几何体的体积为________。
12.一根内径为3cm的圆柱形长试管中装满了水,现把试管中的水逐渐滴入一个内径为8cm、高为1.8cm的圆柱形玻璃杯中,当玻璃杯装满水时,试管中的水的高度下降了________cm.
13.两个底面积相等的圆柱和圆锥形杯子,其中圆柱形杯子的 12 盛有水,将水倒入圆锥形的杯子中刚好倒满,则圆柱形杯子的高与圆锥形杯子的高的比是________。
14.如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN= 13 EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是________cm.
三、解答题
15.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是________;
(2)根据图中所给信息,求该几何体的表面积.(结果保留 π )
16.一个盖着瓶盖的瓶子里面装着一些水(如下图所示),请你根据图中标明的数据,计算瓶子的容积.
17.如图是一张长方形纸片, AB 长为 3cm , BC 长为 4cm .
(1)若将此长方形纸片绕它的一边所在直线旋转一周,则形成的几何体是________;
(2)若将这个长方形纸片绕 AB 边所在直线旋转一周,则形成的几何体的体积是________ cm3 (结果保留 π );
(3)若将这个长方形纸片绕它的一边所在直线旋转一周,求形成的几何体的表面积(结果保留 π ).
18.用如图所示的甲、乙、丙木板做一个长、宽、高分别为a厘米,b厘米,h厘米的长方体有盖木箱(a>b),其中甲刚好能做成箱底和一个长侧面,乙刚好能做成一个长侧面和一个短侧面,丙刚好能做成箱盖和一个短侧面。
(1)填空:用含a、b、h的代数式表示以下面积:
甲的面积________;乙的面积________;丙的面积________.
(2)当h=20cm时,若甲的面积比丙的面积大200cm2 , 乙的面积为1400cm2 , 求a和b的值;
(3)现将一张长、宽分别为a厘米、b厘米的长方形纸板(如图①)分割成两个小长方形。左侧部分刚好分割成两个最大的等圆,和右侧剩下部分刚好做成一个圆柱体模型(如图②),且这样的圆柱体模型的高刚好与木箱的高相等。问:一个上述长方体木箱中最多可以放________个这样的圆柱体模型。
答案解析部分
一、单选题
1. D
考点:圆柱的计算,由三视图判断几何体
解:∵正视图和俯视图是矩形,左视图为圆形,
∴可得这个立体图形是圆柱,
∴这个立体图形的侧面积是2π×3=6π,
底面积是:π?12=π,
∴这个立体图形的表面积为6π+2π=8π;
故答案为:D.
分析:从三视图可知正视图以及俯视图为矩形,而左视图为圆形,可以得出该立体图形为圆柱,再由三视图可知圆柱底面圆的半径和高,求出表面积即可.
2. B
考点:圆柱的计算
解:设高变成了xcm,根据题意得
π×(4÷2)2×4=π×(3.2÷2)2×x,
解得x=6.25,
答:高变成了6.25cm.
故答案为:B.
分析:设高变成了xcm,根据圆柱的体积保持不变列出方程求解即可
3. B
考点:几何体的表面积,圆柱的计算
解:根据圆柱的侧面积公式,可得该圆柱的侧面积为:2π×3×5=30πcm2 .
故选B.
分析:圆柱侧面积=底面周长×高.
4.C
考点:圆柱的计算
解:根据圆柱体的体积计算公式,体积=πr2×高=4π×4=16πcm3 . 故选C. 分析:根据面动成体的原理可知旋转后的圆柱体的半径为2cm,根据圆柱体的面积计算公式即可解.
5. D
考点:圆柱的计算
解:由题意可得,
把原来的圆柱截成两个同样的小圆柱后,增加了两个圆面,
故表面积比原来增加了6.28×2=12.56(平方分米),
故选D.
分析:根据题意可知,把原来的圆柱截成两个同样的小圆柱后,增加了两个圆面,从而可以解答本题.
6. B
考点:点、线、面、体及之间的联系,圆柱的计算
解:∵以直线AB为轴旋转一周得到的圆柱体,得出底面半径为4cm,母线长为3cm,
∴圆柱侧面积=2π?AB?BC=2π?3×4=24π(cm2),
∴底面积=π?BC2=π?42=16π(cm2),
∴圆柱的表面积=24π+2×16π=56π(cm2).
故选B.
分析:表面积=侧面积+两个底面积=底面周长×高+2πr2 .
7. B
考点:圆柱的计算
解:∵圆柱的母线长5,侧面积为30π,
∴底面周长为:30π÷5=6π,
则圆柱的底面直径长是:6π÷π=6.
故选:B.
分析:利用圆柱侧面积计算公式,进而求出底面圆的周长,进而得出答案.
8. C
考点:圆柱的计算
解:根据圆柱体积的计算方法和积的变化规律,再根据圆的面积与半径的关系,已知两个圆柱的高相等,两个圆柱体积的比是9:25,所以两个圆柱底面半径的比是3:5.
故选:C.
分析:根据圆柱的体积公式:v=sh,和圆的面积公式:s=πr2 , 圆的面积扩大的倍数等于半径扩大倍数的平方.已知两个圆柱的高相等,两个圆柱体积的比是9:25,所以两个圆柱底面半径的比是3:5.由此解答.
9. C
考点:圆柱的计算
解:把圆柱侧面展开,展开图如图所示,点A、C的最短距离为线段AC的长.
在Rt△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=1.5π,
所以AC= 32+(32π)2=34+π2 ,
故答案为:C.
分析:要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.
10. D
考点:圆柱的计算
解:∵水桶底面半径:铁柱底面半径=2:1,
∴水桶底面积:铁柱底面积=22:12=4:1,
设铁柱底面积为a,水桶底面积为4a,
则水桶底面扣除铁柱部分的环形区域面积为4a﹣a=3a,
∵原有的水量为3a×12=36a,
∴水桶内的水面高度变为 36a4a ?=9(公分).
故选D.
分析:由水桶底面半径:铁柱底面半径=2:1,得到水桶底面积:铁柱底面积=22:12=4:1,设铁柱底面积为a,水桶底面积为4a,于是得到水桶底面扣除铁柱部分的环形区域面积为4a﹣a=3a,根据原有的水量为3a×12=36a,即可得到结论.
二、填空题
11. 3π
考点:圆柱的计算
解:根据三视图可以判断该几何体为圆柱,圆柱的底面半径为1,高为3,
故体积为: πr2h=π×1×3=3π ,
故答案为: 3π .
分析:根据三视图可以判断该几何体为倒放的圆柱,圆柱的底面半径为1,高为3,据此求得其体积即可.
12. 12.8
考点:圆柱的计算,关于圆柱的应用题
解:设试管中的水的高度下降了xcm;
根据题意有: π×1.52×x=π×(82)2×1.8 ;
解之得:x=12.8.
故答案为12.8.
分析:根据题意可知,内径为3cm的圆柱形长试管中水柱少的体积等于内径为8cm、高为1.8cm的圆柱形玻璃杯的体积,用此作为相等关系列方程求解。
13. 2:3
考点:圆锥的计算,圆柱的计算
解: 解:设圆柱和圆锥形杯子的底面积为s,圆柱的高为h1 , 圆锥的高为h2 ,
根据题意得:2×13sh2=sh1 ,
∴h1∶h2=2∶3 ,
∴ 圆柱形杯子的高与圆锥形杯子的高的比是2:3.
故答案为:2:3.
分析:设圆柱和圆锥形杯子的底面积为s,圆柱的高为h1 , 圆锥的高为h2 , 根据题意列出等式,求出h1∶h2=2∶3 , 即可求解.
14. 2π
考点:圆柱的计算
解:根据题意得:EF=AD=BC,MN=2EM= 13 EF,
∵把该正方形纸片卷成一个圆柱,使点A与点D重合,底面圆的直径为6cm,
∴底面周长为6πcm,即EF=6πcm,
则MN= 6π3=2π cm,
故答案为 6π3=2π .
分析:根据题意得到EF=AD=BC,MN=2EM,由卷成圆柱后底面直径求出周长,除以6得到EM的长,进而确定出MN的长即可.
三、解答题
15. (1)圆柱
(2)解:该几何体的的表面积=π×12×2+2π×3=8π.
考点:圆柱的计算,圆柱的展开图
解:(1)该几何体的名称是圆柱,
故答案为:圆柱
分析:(1)根据圆柱的特征求解;(2)先计算侧面,再计算底面,最后相加即可。
16. 解:由已知条件知,第二个图上部空白部分的高为7﹣5=2cm,
从而水与空着的部分的体积比为4:2=2:1.
由第一个图知水的体积为10×4=40,所以总的容积为40÷2×(2+1)=60立方厘米
考点:圆柱的计算
分析:结合图形,知水的体积不变,从而根据第二个图空着的部分的高度是2cm,可以求得水与空着的部分的体积比为4:2=2:1.结合第一个图中水的体积,即可求得总容积.
17. (1)圆柱
(2)48π
(3)解:绕 AB 边所在直线旋转得到的圆柱的底面半径为 4cm ,高为 3cm ,
表面积是: 2π×4×3+42×π=40π(cm2) ;
绕 AD 边所在直线旋转得到的圆柱的底面半径为 3cm ,高为 4cm ,
表面积是: 2π×4×3+32×π=33π(cm2) .
答:形成的几何体的表面积是 40πcm2 或 33πcm2
考点:圆柱的计算
解:(1)圆柱;(2) 绕AB旋转得到的圆柱的底面半径为 4cm ,高为 3cm ,体积 =π×42×3=48πcm3 ;
分析:(1)根据圆柱体的纵截面是长方形,因此长方形纸片绕它的一边所在直线旋转一周,所形成的几何体是圆柱。
(2)将这个长方形纸片绕AB边所在直线旋转一周,可知底面圆的半径为BC的长,母线长为AB的长,再根据圆柱的面积等于底面圆的面积×母线长,列式计算可求解。
(3)分两种情况:绕AB边所在直线旋转得到的圆柱; 绕 AD边所在直线旋转得到的圆柱,再根据圆柱的表面积=圆柱的侧面积+底面圆的面积,然后列式分别求解。
18. (1)ab+ah;ah+bh;ab+bh
(2)解: {(ab+20a)-(ab+20b)=20020a+20b=1400 ,
化简得 {a-b=10a+b=70 ,
解得: {a=40b=30 .
(3)8
考点:列式表示数量关系,矩形的性质,圆柱的计算,二元一次方程组的应用-几何问题
解:(1)甲的面积= ab+ah ,乙的面积= ah ?????+bh; 丙的面积 =ab+bh;
(3)设圆的直径为d,
∵将一张长、宽分别为a厘米、b厘米的长方形纸板(如图①)分割成两个小长方形。左侧部分刚好分割成两个最大的等圆,和右侧剩下部分刚好做成一个圆柱体模型,
∴b=2d,a-d=πd,
∴a=(π+1)d
∵圆柱体模型的高刚好与木箱的高相等,
∴只有比较木箱的上表面有几个正方形ACDF即可,
∴abd2=π+1d·2dd2=2π+1≈8.28
∴可以放两层,
∴b=2r+πr
∴b2r=πr+2r2r=π2+1≈2.57
∴一个上述长方体木箱中最多可以放8个这样的圆柱体模型.
故答案为:8.
分析:(1)根据矩形的面积公式,分别求出甲,乙,丙的面积即可;
(2)根据甲的面积-丙的面积=200cm2 , 乙的面积为1400cm2 , 列出方程组,将h=20cm代入并解出方程组,即可求出a,b的值;
(3)设圆的直径为d,观察图像由已知可得到b=2d,a=(π+1)d,再根据圆柱体模型的高刚好与木箱的高相等,就可得到只有比较木箱的上表面有几个正方形ACDF即可,因此利用木箱的上表面的面积除以正方形ACDF的面积即可求解。
