4.5合并同类项

(共20张PPT)
4.5合并同类项
1. 单项式 - 的系数是 -2 ，次数
是4。　　　 (　 )
2. 多项式 6x3-4x2y+3xy2-y3 的项是 6x3，
4x2y，3xy2，y3。次数是12次。 (　 ) 　
3. m2n 没有系数。　　 (　 )
4. -13是一次一项式。　　 (　 )
×
×
×
×
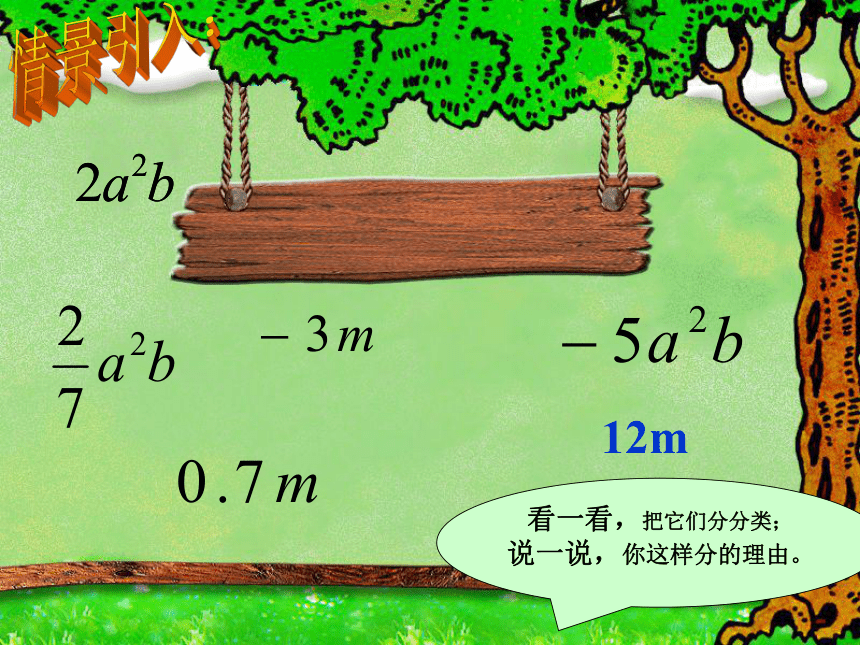
看一看，把它们分分类；
说一说，你这样分的理由。
12m
找一找，它们有什么共同的特点:
1.所含的字母相同
2.相同字母的指数相等
,
12m
,
12 m和 - 3m都含有字母 m，并且 m的指数都是1，我们就把 12m、 -3m 叫做同类项。
12m与 -3m这样所含有的字母相同,
并且相同字母的指数也相同的项,叫做同类项.
所含有的字母相同,并且相同字母的指数也相同的项,叫做同类项.
小结：理解同类项的意义必须注意一个前提和两个条件：
（1）一个前提是“同类项的概念是对整式来说的”，例：1／a与3／a就不能称为同类项，因为它们不是整式。
（2）两个条件是：
①所含有的字母相同；②相同字母的指数也相同
所有的有理数是不是都是同类项？
是
下列各组中的两项是不是同类项？请说明理由。
（1）-3a2b和2b2a (2)3r和πr2
(3)—2.1和3／4 （4）3x和—4y
(5) √2m和—4m (6)3／x和2／x
是
是
不是
不是
不是
不是
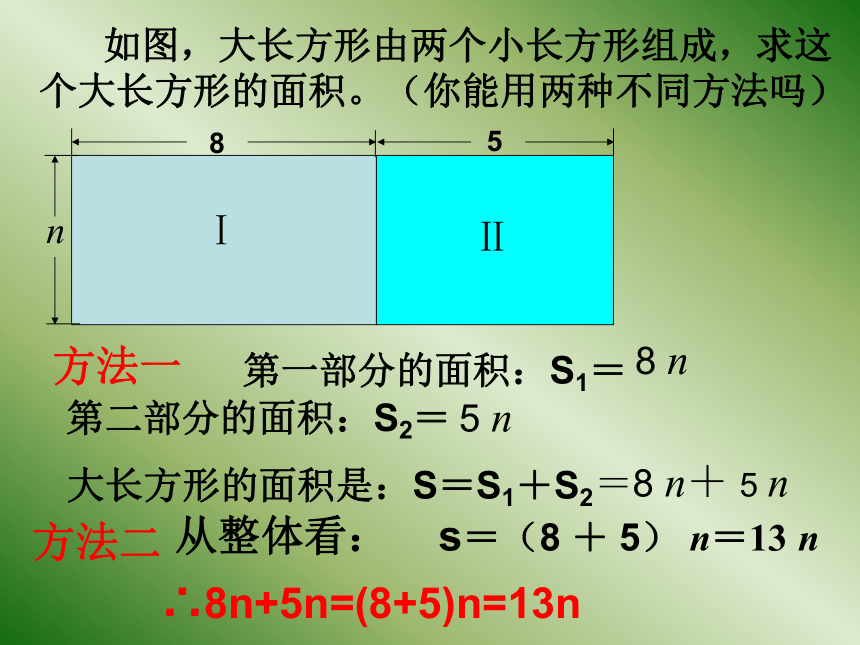
如图，大长方形由两个小长方形组成，求这个大长方形的面积。（你能用两种不同方法吗）
第一部分的面积：S1＝
第二部分的面积：S2＝
大长方形的面积是：S＝S1＋S2
8 n
5 n
＝8 n＋ 5 n
s＝（8 ＋ 5） n＝13 n
8
5
n
Ⅰ
Ⅱ
∴8n+5n=(8+5)n=13n
从整体看：
方法一
方法二
合并同类项: 把同类项合并成一项就叫做合并同类项
从以上两个例子，你能发现合并同类项的方法吗？
方法是：
（1）系数：各项系数相加作为新的系数
（2）字母以及字母的指数不变。
你能举例说明吗？试试看，并与你的同伴交流。
8n+5n=(8+5)n=13n
（可以看作分配律的逆用）
逆用分配律你能化简：—7a2b+5a2b吗？
—7a2b+5a2b=（—7+5）a2b=—2a2b
下列合并同类项对吗 说明理由.
a+a2=a3
3x+5y=8xy
3a2b-a2b=3
x+x+x=3x
错 不是同类项不能合并
错 不是同类项不能合并
对
错 合并时字母和字母的指数不变
例1：合并同类项
方法：（1）系数：各项系数相加作为新的系数
（2）字母以及字母的指数不变。
找
移
并
例.求多项式2a2b-3a-3a2b+2a的值,
已知a=-0.5,b=4
解： 原式= 2a2b-32b-3a+2a
=(2-3)a2b+(-3+2)a
=-a2b-a
当a=-0.5,b=4时，
原式=-(-0.5)2×4－(-0.5)
=-0.25×4+0.5
=-1+0.5=-0.5
先化简，后求值
通过以上的练习
你可以找出合并同类项的要点是什么？
一变一不变
一变就是系数要变
（新系数变为原来各系数的代数和）
一不变就是字母和字母的指数不变
（原来的字母和字母的指数照抄）
若4a2b6+mc5与—3a2b4cn+1是同类项，求：（1）m+n; (2)mn
解：∵ 4a2b6+mc5与—3a2b4cn+1是同类项
∴6+m=4,5=n+1
∴m=—2，n=4
∴(1)m+n=—2+4=2
∴（2）mn=（—2）4=16
小结：
本节课我们学到了什么？
合并同类项我们要注意哪些问题？
怎样合并同类项？
思考题：
一家商店以每a包元的价格买进了30包甲种绿茶，又以每包b元的价格买进了60包乙种绿茶.如果以每包(a+b)/2元的价格卖出这两种茶叶，则卖完后，这家商店( )
(A)赚了；
(B)赔了；
(C)不赔不赚；
(D)不能确定赚或赔.
(D)不能确定赚或赔.
90×(a+b)/2－(30a+60b)
=45(a+b) －(30a+60b)
=45a+45b－30a－60b
=15a－15b=15(a－b).
(1)当a=b时，15(a－b)=0, 不赔不赚；
(2)当a>b时，15(a－b)>0, 赚了；
(3)当a例2. 合并同类项：
你认为下列哪些整式可以分成一类？并说明理由
（1）2xy （2）—5x (3)3x （4）—5yx (5)5x2y (6)—3y2x
(7)7x2y (8)6xy2 （9）8y (10)5y
解： 2xy 与—5yx 一类； —5x 与3x 一类；5x2y 与7x2y一类； —3y2x与6xy2一类；
8y与5y一类。
(1) x与 y ,(2)a2 b与ba 2 ，
(3)3 pq 与-3 pq ，(4)9 bc与9a c ，
(5) a 2 与a 3 是不是同类项？请说明理由。
你能自己举出一些同类项的例子吗？