5.3 一元一次方程的应用(1)

(共35张PPT)
5.3一元一次方程的应用(1)
2008年奥运会上，我国获得51枚金牌。比2004年奥运会我国获得的金牌数的2倍少13枚。问：2004年奥运会我国获得几枚金牌？
（51+13）÷2=32
2x-13=51
例1 5位教师和一群学生一起去看足球赛，教师门票按全票价每人70元，学生只收半价。如果门票总价910元，那么学生有多少人？
分析：题中涉及的数量有：
人数、票价、总价。
题中的相等关系有：
人数×票价=总票价
教师的总票价+学生的总票价=910
解：设学生有x人，根据题意，得
5×70+ ×70x=910
2
1
例1 5位教师和一群学生一起去看足球赛，教师门票按全票价每人70元，学生只收半价。如果门票总价910元，那么学生有多少人？
解这个方程，得 x=16
检验：x=16适合方程，且符合题意。
答：学生有16人。
运用方程解决实际问题的一般过程：
1审题：分析题意，找出题中的数量极其关系；
2设元：选择一个适当的未知数用字母表示（例如x）；
3列方程：根据相等关系列出方程；
4解方程：求出未知数的值；
5检验：检查求得的值是否正确和符合实际情形，并写出答案。
练习1.若小明每秒跑4米，那么他5秒能跑_____米.
2.小明用4分钟绕学校操场跑了两圈(每圈400米)，那么他的速度为_____米/分.
3.已知小明家距离火车站1500米，他以4米/秒的速度骑车到达车站需要_____分钟.
20
200
6－
1
4
时间=路程÷速度
例2：小聪和小张每天早晨坚持跑步，小聪每秒跑4米，小张的速度是小聪的1.5倍。
如果他们站在百米跑道的两端同时相向起跑，那么几秒后两人相遇？
分析：题中涉及到的数量有速度、路程、时间。
速度×时间=路程
小聪跑的路程+小张跑的路程=100
相等关系有：
解：设x秒后两人相遇。根据题意，得
4x+1.5×4x=100
解这个方程，得 x=10
检验：x=10适合方程，且符合题意。
答;10秒后两人相遇。
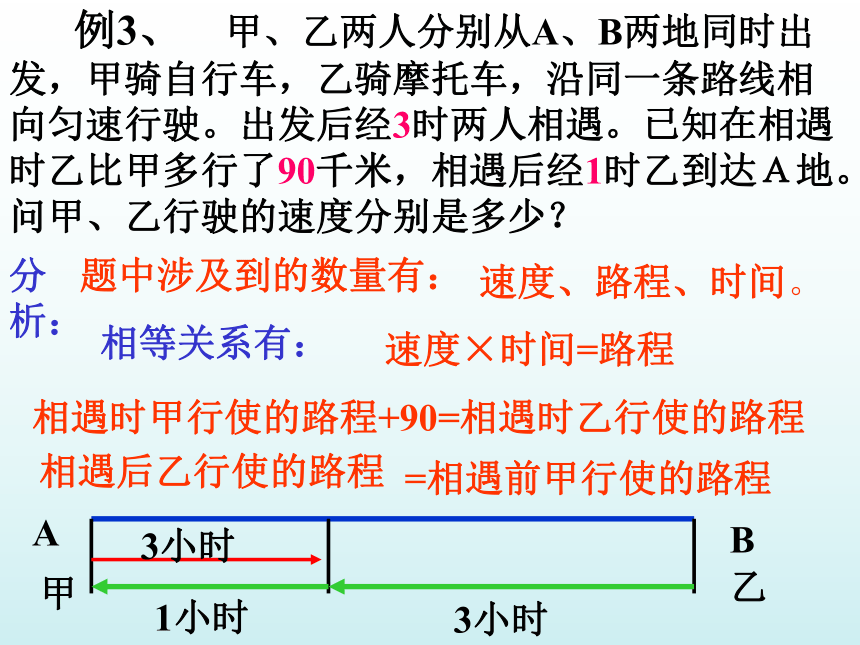
　例3、　甲、乙两人分别从A、B两地同时出发，甲骑自行车，乙骑摩托车，沿同一条路线相向匀速行驶。出发后经3时两人相遇。已知在相遇时乙比甲多行了90千米，相遇后经1时乙到达Ａ地。问甲、乙行驶的速度分别是多少？
分析：
题中涉及到的数量有：
速度、路程、时间。
相等关系有：
速度×时间=路程
相遇时甲行使的路程+90=相遇时乙行使的路程
相遇后乙行使的路程
=相遇前甲行使的路程
A
B
甲
乙
3小时
3小时
1小时
例3、甲、乙两人分别从A、B两地同时出发，甲骑自行车，乙骑摩托车，沿同一条路线相向匀速行驶。出发后经3时两人相遇。已知在相遇时乙比甲多行了90千米，相遇后经1时乙到达Ａ地。问甲、乙行驶的速度分别是多少？
解：设甲行使的速度为x千米／时，
则相遇时甲行使的路程为3x千米，
相遇时乙行使的路程为（3x+90）千米，
乙行使的速度为 千米／时，
3
3x+90
根据题意，得
3
3x+90
=3x
解这个方程，得 x=15
检验：x=15适合方程，且符合题意。
将x=15代入
3x+90
3
=45
答：甲行使的速度为15千米／时，乙行使的速度为45千米／时
例3、甲、乙两人分别从A、B两地同时出发，甲骑自行车，乙骑摩托车，沿同一条路线相向匀速行驶。出发后经3时两人相遇。已知在相遇时乙比甲多行了90千米，相遇后经1时乙到达Ａ地。问甲、乙行驶的速度分别是多少？
解：设乙行使的速度为y千米／时，
则相遇时乙行使的路程为3y千米，
则相遇后乙行使的路程为y千米，
3y=y+90
解这个方程，得 y=45
检验：y=45适合方程，且符合题意。
根据题意，得
将y=45代入,
y／3=15
答：甲行使的速度为15千米／时，乙行使的速度为45千米／时
例3、甲、乙两人分别从A、B两地同时出发，甲骑自行车，乙骑摩托车，沿同一条路线相向匀速行驶。出发后经3时两人相遇。已知在相遇时乙比甲多行了90千米，相遇后经1时乙到达Ａ地。问甲、乙行驶的速度分别是多少？
解：设相遇时甲行使的路程为z千米,
则相遇时乙行使的路程为z+90千米。
相遇后乙行使1小时的路程z千米，
因此乙的速度为z千米／小时，
故相遇时乙行使的路程为3z千米
根据题意，得
Z+90=3z
解这个方程，得 z=45
检验：z=45适合方程，且符合题意。
小明所跑的路程
小彬所跑的路程
小明
小彬
+
=100
小明所跑的路程
小彬所跑的路程
100米
相遇
练习:小彬和小明每天早晨坚持跑步，小明每秒跑6米，小彬每秒跑4米。
(1)如果他们站在百米跑道的两端同时相向起跑，那么几秒后两人相遇？
(2)如果小明站在百米跑道的起点处，小彬站在他前面10米处，两人同时同向起跑，几秒后小明能追上小彬？
● 请编一个实际应用题，要求所列的方程为15x+45x=180.
我知道了…………
　我感到困难是…………
(2)解决实际问题的一般过程：
(1)解应用题要学会借助线段图
来分析数量关系;
审
设
列
解
验
作业：
1.完成P126 作业题 ；
2.完成《作业本》（１）５.３（一）；
1、三个连续奇数的和为57，求这三个数。
解:设三个连续奇数中最小的一个为x,
则其余两个为（x+2）、(x+4)
根据题意，得
X+(x+2)+(x+4)=57
解这个方程，得 x=17
检验：x=17适合方程，且符合题意。
将x=17代入x+2=19、x+4=21
答：这三个连续奇数分别为17、19、21.
2、甲、乙两人从相距为180千米的A、B两地出发，甲骑自行车，乙骑摩托车，沿同一条路线相向行驶，已知甲的速度为每小时15千米，乙的速度为每小时45千米。如果甲先行1时后乙才出发，问甲再行多少时间相遇？
分析：
A
B
180千米
1时
甲行使的路程
乙行使的路程
？
？
11／4小时
行程问题中常用的分析方法是画线段图分析法
2、甲、乙两人从相距为180千米的A、B两地出发，甲骑自行车，乙骑摩托车，沿同一条路线同向行驶，已知甲的速度为每小时15千米，乙的速度为每小时45千米。如果甲先行1时后乙才出发，（1）问经过多少时间乙追上甲？
A
B
180千米
1小时
甲行使的路程
乙行使的路程
？
？
X=6.5小时
（2）问：甲出发几小时后，乙追上甲？
2、甲、乙两人从相距为180千米的A、B两地同时出发，甲骑自行车，乙骑摩托车，沿同一条路线相向行驶，已知甲的速度为每小时15千米，乙的速度为每小时45千米。问：经过几小时两人相距30千米？
A
B
180千米
30千米
A
B
30千米
2.5小时
3.5小时
练习：A、B两地相距120千米，甲骑自行车以每小时行10千米从A地出发去B地，乙骑摩托车以每小时50千米从B地出发去A地，甲、乙同时出发。问：
（1）经过多少时间甲、乙两人相距60千米？
（2）若甲先出发1小时，则甲出发后几小时，两人相距50千米？
解：（1）设经过x小时甲、乙两人相距60千米
10x+50x=120-60
X=1
10x+50x=120+60
X=3
(2)设则甲出发后y小时，两人相距50千米，
10y+50(y-1)=120-50
Y=2
10y+50(y-1)=120+50
Y=22／6
如设则乙出发后z小时，两人相距50千米，又如何列方程？
3.“钱塘江尽到桐庐,水碧山青画不如”.自古以来连接桐庐到杭州的富春江就是重要的黄金水道.“两岸青山,山为水铸情,满目葱翠;一江春水,水因山溢美,澄如湖海碧如天.”一旅游船从桐庐东门码头出发顺流而下驶往杭州滨江码头用去5小时,从杭州滨江码头逆流而上到桐庐东门码头用去7小时,水流速度为3千米 小时. 求桐庐东门到杭州的滨江码头的距离.
分析：
题中涉及到的数量有：
速度、路程、时间。
相等关系有：
速度×时间=路程
旅游船的速度+水流速度=顺流速度
旅游船的速度-水流速度=逆流速度
／
顺流行驶的路程=逆流行驶的路程
解:设旅游船的速度为x千米 小时
／
5(x+3)=7(x-3)
X=18
5(x+3)=105
间接设元法
4.一队学生去校外进行军事野营训练。他们以5千米／小时的速度行进，走了18分钟的时候，学校要将一个紧急通知传给队长。通讯员从学校出发，骑自行车以14千米／小时的速度按原路追上去。通讯员用多少时间可以追上学生队伍？
解;设通讯员用x小时可以追上学生队伍，
根据题意，得
60
18
×5+5x=14x
解这个方程，得 x=1／6
检验：x=1／6适合方程，且符合题意。
答：通讯员用1／6小时可以追上学生队伍？
5.姐妹俩同时从家里出发到少年宫，路程全长770米，妹妹步行速度每分钟60米，姐姐骑自行车以每分钟160米的速度到达少年宫后立即返回，途中与妹妹相遇。这时妹妹走了几分钟？
解：设妹妹走了x分钟，根据题意，得
60x+(160-770)=770
或60x+160x=2×770
解这个方程的，得 x=7
检验：x=7适合方程，且符合题意。
答：妹妹走了7分钟.
家
少年宫
练习：A、B两地相距120千米，甲骑自行车，乙骑摩托车都从A地出发，同向而行，甲比乙早出发2小时，甲每小时行15千米，乙每小时行60千米.
(1)甲出发后多少小时，乙追上甲？
(2)乙到达B地后立即返回，途中在何处遇上甲？
解：(1)设甲出发后x小时，乙追上甲,
15x=60(x-2)
X=8／3
若设乙出发后x小时，乙追上甲,又怎样做？
（2）设甲出发y小时，乙在返回途中遇上甲
60（y-2）+15y=2×120
Y=24／5
15y=15×24／5=72千米
设乙出发y小时，在返回途中遇上甲，又怎样做？
6.火车用26秒的时间通过一条256米的隧道
这列火车又以16秒的时间通过一条96米米的桥梁，求这列火车的速度及长度（假设火车的速度不变）。
（即从车头进入入口至车尾离开出口），
解：设火车的长度为x米，根据题意，得
256+x
26
16
96+x
=
解这个方程的，得x= 160
检验：x=160适合方程，且符合题意。
16
96+x
=
16
答;这列火车的速度16米／秒，长度为160米。
方法一根据速度相等列方程
6.火车用26秒的时间通过一条256米的隧道
这列火车又以16秒的时间通过一条96米米的桥梁，求这列火车的速度及长度（假设火车的速度不变）。
（即从车头进入入口至车尾离开出口），
解：设火车的速度为y米／秒，根据题意，得
26y-256=16y-96
解这个方程的，得y= 16
检验：x=16适合方程，且符合题意。
26y-256=160
答;这列火车的速度16米／秒，长度为160米。
根据火车长度相等列方程
7.一条环形跑道长400米，甲练习骑自行车，平均每分钟骑550米，乙练习赛跑，平均每分钟跑250米。（1）若两人同时从同地同向出发，则经过多少分钟甲第一次追上乙.（2）若两人同时从同地相向出发，则经过多少分钟甲、乙第一次相遇。.
解;(1)设经过x分钟甲第一次追上乙，
550x-250x=400
解：（2）设经过y分钟甲、乙第一次相遇。.
550y+250y=400
第100次追上或相遇时又怎样呢？
练习：甲，乙两人在环形跑道上练习跑步，已知环形跑道一圈长400米，乙每秒跑6米，甲每秒跑8米，如果甲在乙前面8米处，同时同向出发。
（1）经过多少秒两人首次相遇？（2）经过多少秒两人首次相距100米，第二次相距10米？
解：(1)设经过x秒两人首次相遇,
8x-(6x-8)=400
X=196秒
100+6y=8y+8
(2)设经过y秒两人首次相距100米
Y=46
8z-(6z-8)=400-10
z=191
(2)设经过z秒两人第二次相距10米
第三次相距10米，又怎样做？
8z-(6z-8)=400+10