5.3 一元一次方程应用(2)

(共33张PPT)
一元一次方程的应用(2)
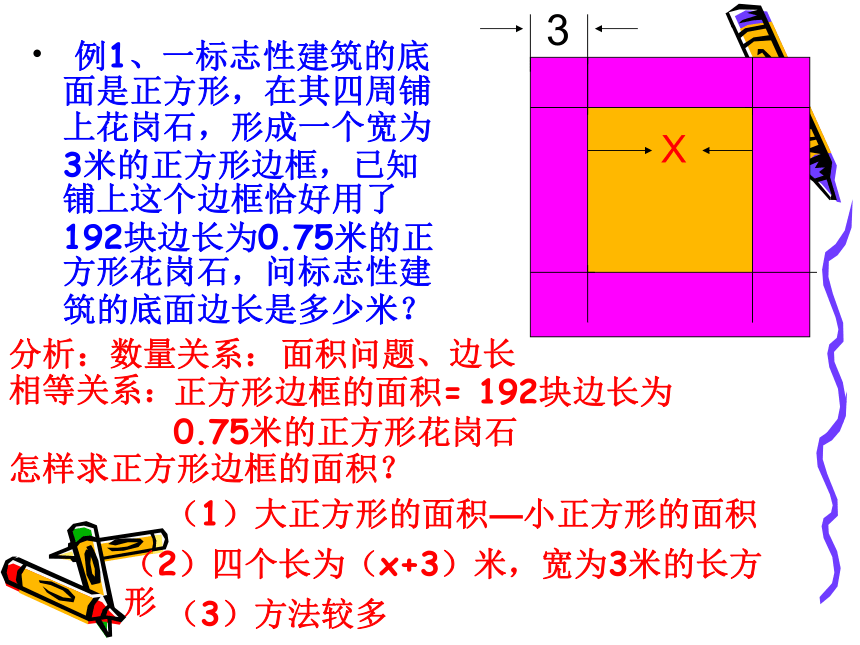
例1、一标志性建筑的底面是正方形，在其四周铺上花岗石，形成一个宽为3米的正方形边框，已知铺上这个边框恰好用了192块边长为0.75米的正方形花岗石，问标志性建筑的底面边长是多少米？
3
X
分析：数量关系：
面积问题、边长
相等关系：
正方形边框的面积= 192块边长为0.75米的正方形花岗石
怎样求正方形边框的面积？
（1）大正方形的面积—小正方形的面积
（2）四个长为（x+3）米，宽为3米的长方形
（3）方法较多
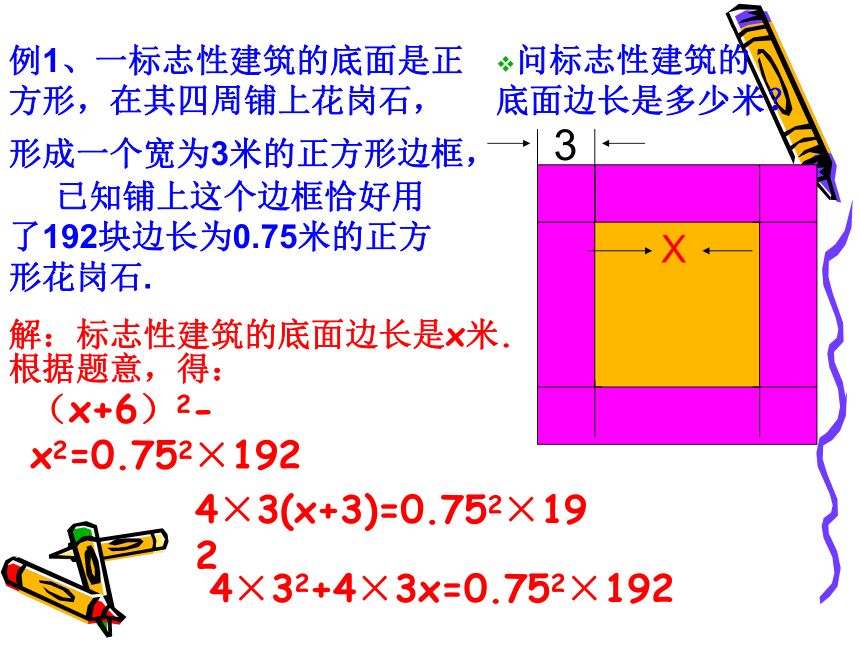
例1、一标志性建筑的底面是正方形，在其四周铺上花岗石，
形成一个宽为3米的正方形边框，
已知铺上这个边框恰好用了192块边长为0.75米的正方形花岗石.
问标志性建筑的底面边长是多少米？
3
X
解：标志性建筑的底面边长是x米.
根据题意，得：
（x+6）2-x2=0.752×192
4×3(x+3)=0.752×192
4×32+4×3x=0.752×192
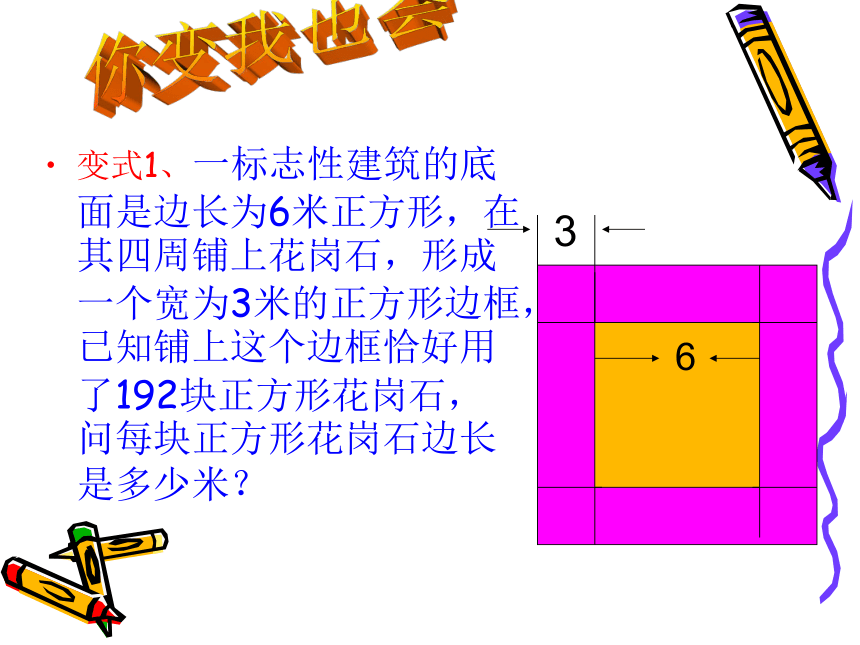
变式1、一标志性建筑的底面是边长为6米正方形，在其四周铺上花岗石，形成一个宽为3米的正方形边框，已知铺上这个边框恰好用了192块正方形花岗石，问每块正方形花岗石边长是多少米？
3
6
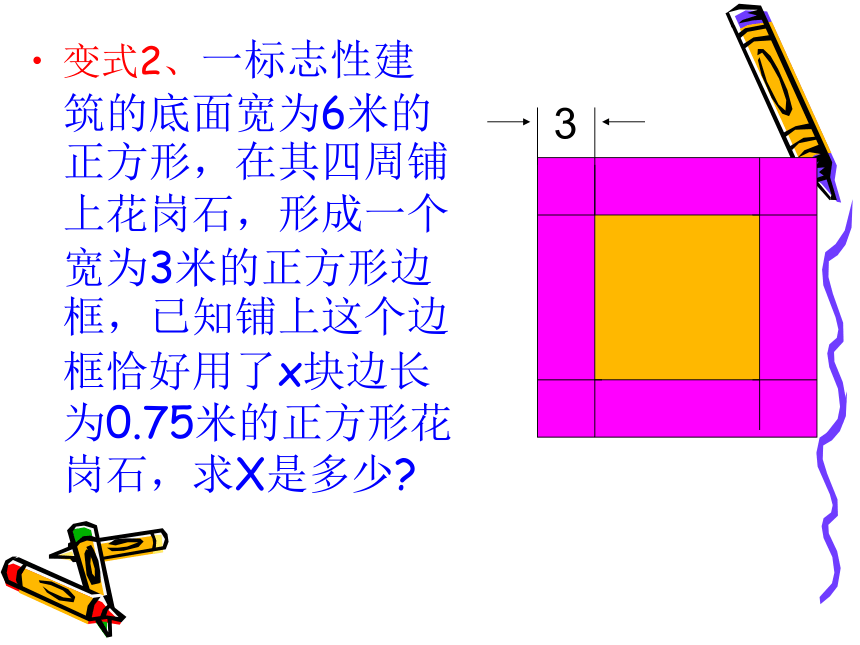
变式2、一标志性建筑的底面宽为6米的正方形，在其四周铺上花岗石，形成一个宽为3米的正方形边框，已知铺上这个边框恰好用了x块边长为0.75米的正方形花岗石，求X是多少
3
练习
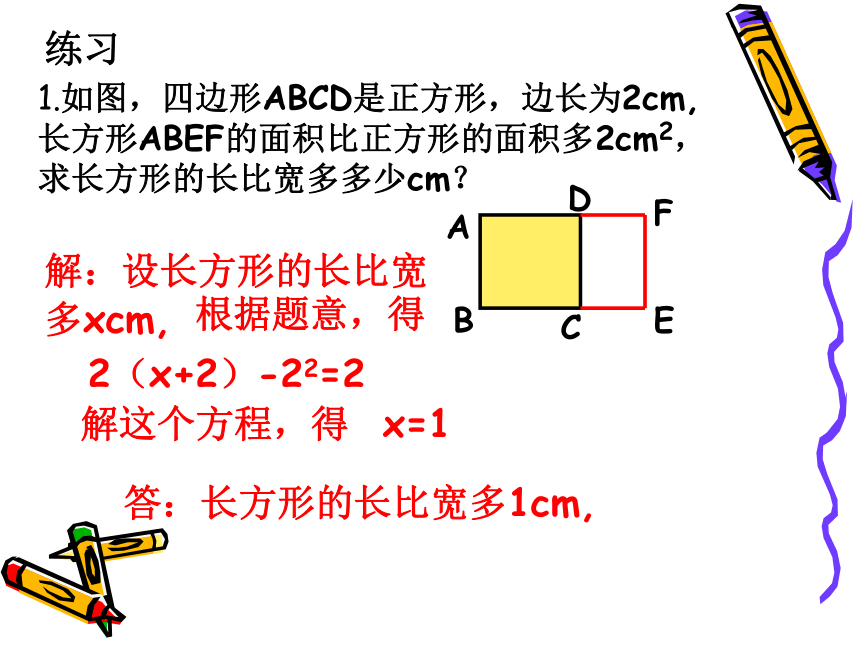
1.如图，四边形ABCD是正方形，边长为2cm,长方形ABEF的面积比正方形的面积多2cm2，求长方形的长比宽多多少cm？
A
B
D
C
E
F
解：设长方形的长比宽多xcm,
根据题意，得
2（x+2）-22=2
解这个方程，得 x=1
答：长方形的长比宽多1cm,
2.把一个边长为25厘米的正方形铁丝框重新围成长方形。使得该长方形的长比宽多14厘米，此时的长、宽是多少？
解：设长方形的宽为x厘米，则长为（x+14）厘米。
根据题意，得
2〔x+(x+14)〕=4×25
解这个方程，得 x=18
X+14=18+14=32
答：长为32厘米，宽为18厘米。
例 2、学校组织植树活动，已知在甲处植树的有23人，乙处植树的有17人，现调20人去支援，使甲处植树的人数是乙处植树的人数2倍，应调往甲、乙两处各多少人？
分析
涉及数量有：
甲、乙两地原有人数、支援人数、增加后人数
相等关系有：
甲处增加后的人数=2×乙处增加后的人数
甲处
乙处
原有人数
增加人数
增加后人数
23
17
x
20-x
23+x
17+(20-x)
解：设调往甲处x人，根据题意，得
23+x=2〔17+（20-x）〕
解这个方程，得 x=17
∴20-x=3
答：应调往甲处17人，调往乙处3人，
如果设调往乙处x人，方程该怎么列？
解：23+（20-x）=2(17+x)
调配问题用列表分析数量关系是常用方法。
变式1、学校组织植树活动，已知在甲处植树的有23人，乙处植树的有17人，现调20人去支援，使甲处植树的人数是乙处植树的人数3倍，应调往甲、乙两处各多少人？
23+x=3〔17+（20-x）〕
解这个方程，得x=22
解：设调往甲处x人，根据题意，得
＞20
故此题无解
变式2、学校组织植树活动，已知在甲处植树的有23人，乙处植树的有17人，现调20人去支援，使甲处植树的人数是乙处植树的人数n倍(n为整数），应调往甲、乙两处各多少人？
解：设调往甲处x人，根据题意，得
23+x=n〔17+（20-x）〕
解这个方程，得x=37-
n+1
60
1.有甲、乙两个牧童，甲对乙说；“把你的羊给我1只，我的羊数就是你的羊数的二倍。”乙回答说：“最好还是把你的羊给我一只，这样我们的羊就一样多了。”两个牧童各有几只羊？
分析
甲的羊数+1=2（乙的羊数-1）
甲的羊数-1=乙的羊数+1
解：设乙牧童有羊x只，
则甲牧童有羊（x+2）只，
根据题意，得
(x+2)+1=2(x-1)
解这个方程，得 x=5
答：甲、乙两个牧童各有7只和5只羊
2.某车间22名工人生产螺钉和螺母，每人每天平均生产1200个螺钉或2000个螺母，一个螺钉配两个螺母，为了使每天生产的产品刚好配套，应该如何安排工人生产？
解：设每天安排x名工人生产螺钉，则（22-x）名工人生产螺母。
根据题意，得
2×1200x=2000× (22-x)
解这个方程，得 x=10
22-x=22-10=12
答：应该10人生产螺钉，12人生产螺母。
◆41人参加运土劳动，有30根扁担，安排多少人抬，多少人挑，可使扁担和人数相配不多不少？
解：设有x人挑土，根据题意，得
X+ =30
2
41-x
解这个方程，得x=19
答：安排22人抬，19人挑，可使扁担和人数相配不多不少。
41-x=41-19=22
▲甲、乙两处共有煤220吨，因供给需求，要从甲处调往乙处45吨煤，使乙处煤的吨数比甲处多两倍，问甲、乙两处原有多少煤？
解：设甲处原有煤x吨，根据题意，得
3（x-45）=（220-x）+45
解这个方程，得x=100
∴220-x=220-100=120
答：甲处原有煤100吨，乙处原有煤120吨
3.每年3月12日是植树节，某校在植树活动中种了杨树和杉树两类树。已知种植杨树的棵数比总数的一半多56棵，杉树比总数的三分之一少14棵。两类树各种多少棵？
解：两类树共种x棵.
根据题意，得
（ x+56）+( x-14)=x
2
1
3
1
解这个方程，得x=252
2
1
X+56=182
杉树252-182=70
答：杨树种植182棵，杉树种植70棵。
4.汽车队运送一批货物，每辆装4吨还有7吨未装；每辆装5吨，最后一辆车余下2吨未装满。这个车队有多少辆车？这批货物共有多少吨？
解;这个车队有x辆车,
则这批货物共有(4x+7)吨
根据题意，得
4x+7=5(x-1)+3
或4x+7=5x-2
解这个方程，得x=9
4x+7=4×9+7=43
答;这个车队有9辆车,这批货物共有43吨.
1.一些人分苹果，如果每人分5 只，那么会剩下15只；如果每人分6只，那么还缺少17只，问有多少 人？多少只苹果？
解：设有x人，
则苹果有(5x+15）只
根据题意，得
5x+15=6x-17
解这个方程，得 x=32
答：有多32人,175只苹果
5x+15=5×32+15=175
1.一些人分苹果，如果每人分5 只，那么会剩下15只；如果每人分6只，那么还缺少17只，问有多少只苹果？
解：设有苹果x只，根据题意，得
=
X-15
X+17
6
5
解这个方程，得x=175
答：有175只苹果。
◆有一箱玩具分给一群小朋友，若每人4个则多13个，若每人5个则少12个，设小朋友为x个。根据题意可列方程_______________
4x+13=5x-12
▼某小组为开展体育活动，准备购买篮球、兵乓球、羽毛球等运动器材，所需费用由全组同学分担，若每人付20元，则多17元。后来组长向每人收了19元，自己多付了5元。问这个小组共有多少名同学？
解：设这个小组共有x人，根据题意，得
20x-17=19x+5
解这个方程，得x=22
答：这个小组共有22人。
某校七年级甲、乙两个班共103人（其中甲班人数多于乙班人数）去景点游玩，如果两班都以班为单位分别购票一共需付4810元
(1)如果两班联合起来，作为一个团体购票，可以节省多少钱？
(2)两班各有多少学生？
1、某景点门票价格如下表：
购票人数（人） 1—50人 51—100人
100人以上
每人门票价格（元） 50 45 40
解：（1）4810-40×103=690
答：作为一个团体购票，可以节省690元钱？
1、某景点门票价格如下表：
购票人数（人） 1—50人 51—100人
100人以上
每人门票价格（元） 50 45 40
某校七年级甲、乙两个班共103人（其中甲班人数多于乙班人数）去景点游玩，如果两班都以班为单位分别购票一共需付4810元
(2)两班各有多少学生？
解：设甲班有x人，则乙班有（103-x）人
∵甲班人数多于乙班人数,
∴x≥52.
乙班人数≤51
Ⅰ：当甲班有52人，乙班有51人时，
51×45+52×45=4635
≠4810，
∴不成立
Ⅱ：当甲班人数在53—100时，
45x+50(103-x)=4810
解这个方程，得 x=68
103-x=103-68=35
Ⅲ：当甲班人数在100人以上，
乙班人数在1—50人时
乙班人数在1—50时，
40x+50(103-x)=4810
解这个方程，得 x=34
，符合题意
答：甲班有68人，乙班有35人
（舍去）
2.已知某电脑公司有A型、B型、C型三种型号的电脑，其价格分别为A型每台6000元，B型每台4000元，C型每台2500元，我市学军中学计划将100500元钱全部用于从该电脑公司购进其中两种不同型号的电脑36台，请你设计出几种不同的购买方案供该校选择，并说明理由。
解：Ⅰ：设购买A型电脑x台，B型电脑（36-x）台
6000x+4000(36-x)=100500
解这个方程，得x= —21.75
（舍去）
Ⅱ：设购买A型电脑x台，c型电脑（36-x）台
6000x+2500(36-x)=100500
解这个方程，得x= 3
36-x=36-3=33
Ⅲ：设购买B型电脑y台，c型电脑（36-y）台
4000y+2500(36-y)=100500
解这个方程，得y= 7
36-y=36-7=29
答：有两种购买方案;第一种A型3台，C型33台；第二种B型7台，C型29台
3、北京和上海各有大型计算机若干台，北京可支援外地10台，上海可支援外地4台，现决定给重庆8台，武汉6台，从北京、上海将计算机运往重庆、武汉的费用如右图所示，已知，有关部门计划用80000元费用运送这些计算机（1）请你设计一种方案，使武汉、重庆能得各自所需的计算机，而且运费正好够用（2）你能否修改方案，降低整个费用
武汉 重庆
北京 4 8
上海 3 5
终点
起点
◇小华在日历中发现他生日那天的上、下、左、右四个日期的和为48，则小华的生日是_______号。
12
◆在日历上圈出一个在竖列上相邻的3个数，使得它们的和为69。则这3天分别是________________
16、23、30
★在日历上，用一个正方形任意圈出3×3个数，那么这9个数的和可能是 （ ）
A、80 B、98 C、108 D、206
c
▲在足球甲B联赛得前11场比赛中，某队仅负一场，共积22分。按比赛规则，胜一场得3分，平一场得1分，负一场得0分，则该队共胜了_____场。
6
■一张试卷有25道选择题，满分100分，若做对一题得4分，做错或不做一题倒扣1分，某同学得了85分，那么他做对的题数是（ ）
A、23 B、22 C、21 D、20
B
●一次知识竞赛，要求两队各答10个问题，组委会给每个队的底分是100分，并规定答对一题加10分，答错一题减10分。结果甲队以180分获胜，则甲队答对了________题。
9
■一张试卷有25道，若做对一题得4分，做错一题扣1分，某同学得了70分，那么他做对的题数是（ ）
A、17 B、18 C、19 D、20
c
■一张试卷有20道选择题，若做对一题得8分，做错一题扣5分，不做得0分，某同学得了100分，那么他做对的题数是______题，没做的题目有_______题
15
1
▲在足球甲B联赛得前14场比赛中，某队仅负5场，共积19分。按比赛规则，胜一场得3分，平一场得1分，负一场得0分，则该队共胜了_____场。
5
4.甲、乙两个圆柱形容器，底面积之比为5：3，甲容器水深20厘米，乙容器水深10厘米，再往两个圆柱形容器注入同样多的水，使两个圆柱形容器的水深相等，这时水深多少厘米？
解：设这时水深h厘米,
甲、乙两个圆柱形容器的底面积分别为5a和3a。根据题意，得
5a×(h-20)=3a×(h-10)
解这个方程，得 h=35
答：水深35厘米
6.两根竹竿，长度分别为2米和3米，若要把它们绑接成长度为4.2米的竹竿，则重叠部分的长度为____________
0.8米
（部分量+部分量=总量+重叠部分）
7.甲、乙、丙三数之比是2:3:7,三数之和是48，则这三数分别是______________
8、12、28
8、甲、乙两列火车，甲车长200米，乙车长280米，在平行轨道上相向而行，已知两车自车头相遇到车尾相离共需18秒，甲、乙两车的速度之比为5：3。求两车的速度。
●某公路站的收费标准时大车10元，小客车6元，轿车3元，某天通过收费站的大车、小客车、轿车的数量比为5：6：7，共收费642元，问这天通过收费站的三种汽车各多少辆？
3.用一根直径为12厘米的圆柱形铝柱，锻造10只直径为12厘米的铝球，问应截取多长的铝柱？
解：设应截取h厘米长的铝柱
根据题意，得
10× ∏×63=∏×62h
3
4
解这个方程，得h=80
答;应截取80厘米长的铝柱
5.在一个底面半径为20厘米的圆柱体水桶里，有一个底面半径为10厘米的圆柱体钢材完全放在水中，当圆柱体钢材从水中取出后，水桶里的水面下降了3厘米，求这段钢材的长度是多少厘米？
解:设这段钢材的长度是h厘米,根据题意，得
∏×202×3= ∏×102h
解这个方程，得 h=12
答;这段钢材的长度是12厘米