锐角三角函数复习
图片预览


文档简介
(共21张PPT)
如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,你能根据这些条件求出南峰塔的高度吗
一、基本概念
1.正弦
A
B
C
a
c
sinA=
2.余弦
b
cosA=
3.正切
tanA=
锐角A的正弦、余弦、正切、都叫做∠A的锐角三角函数.
定义:
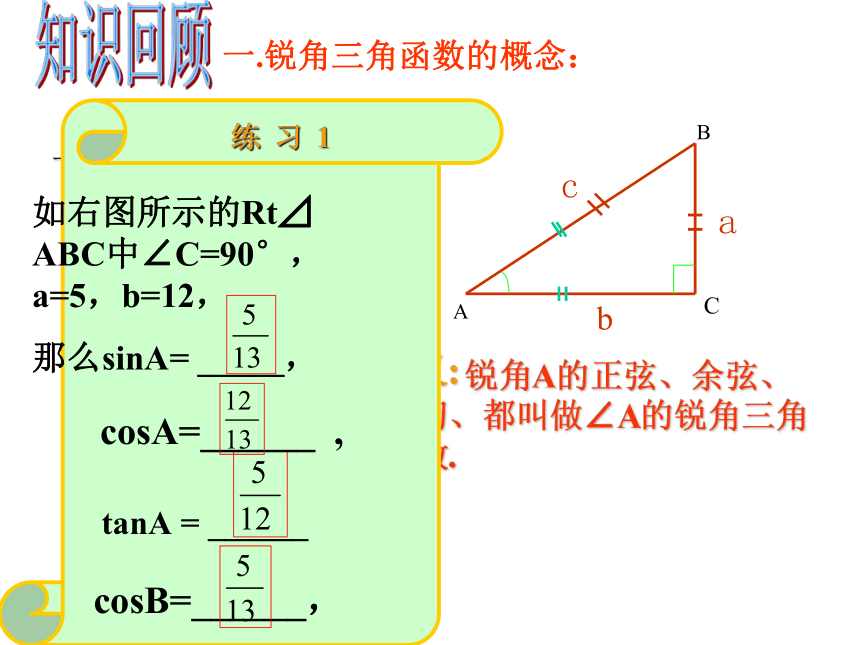
练 习 1
如右图所示的Rt⊿ ABC中∠C=90°,a=5,b=12,
那么sinA= _____,
tanA = ______
cosB=______,
cosA=______ ,
一.锐角三角函数的概念:
tanα
cosα
sinα
6 0°
45 °
3 0°
角 度
三角函数
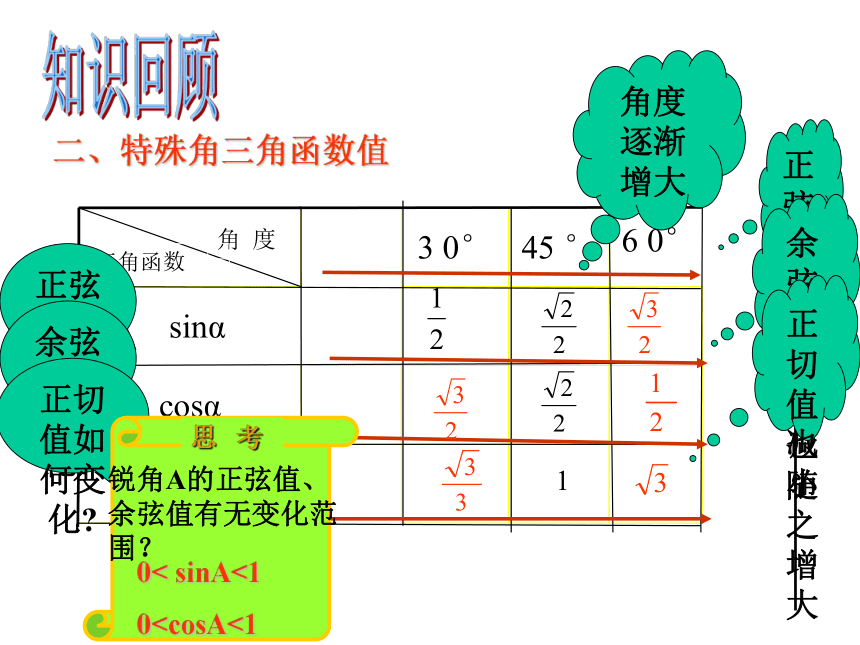
二、特殊角三角函数值
1
角度
逐渐
增大
正弦值如何变化
正弦值也增大
余弦值如何变化
余弦值逐渐减小
正切值如何变化
正切值也随之增大
思 考
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0=2 + d
= 2
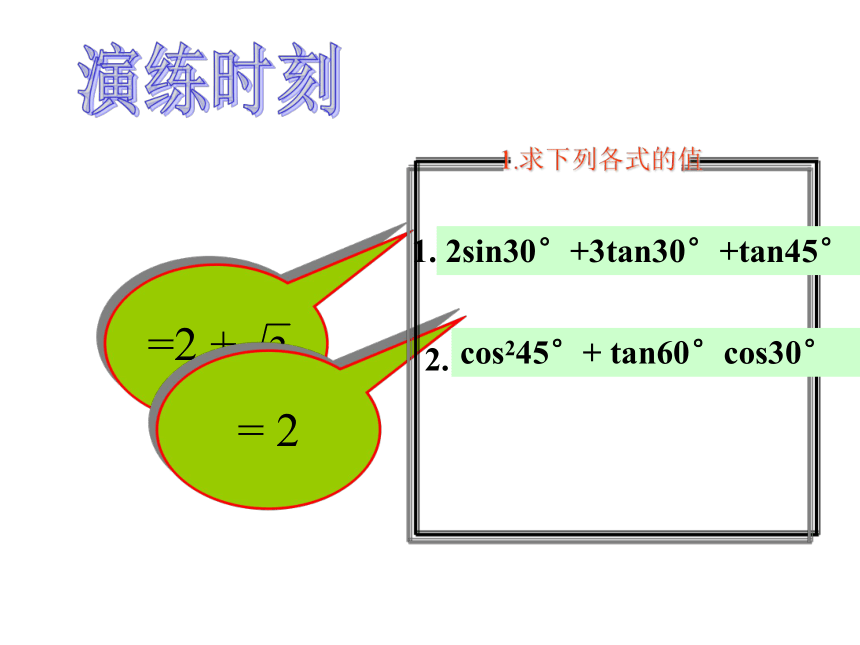
1.求下列各式的值
2sin30°+3tan30°+tan45°
cos245°+ tan60°cos30°
1.
2.
2.在△ABC中,∠C=90°,tanA= 则sinB=( )
D
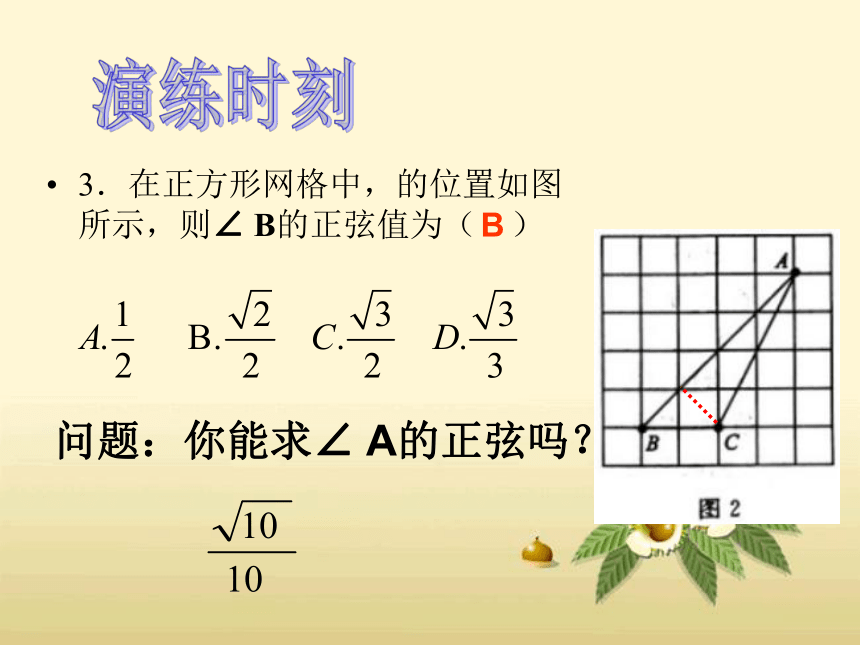
3.在正方形网格中,的位置如图所示,则∠ B的正弦值为( )
问题:你能求∠ A的正弦吗?
B
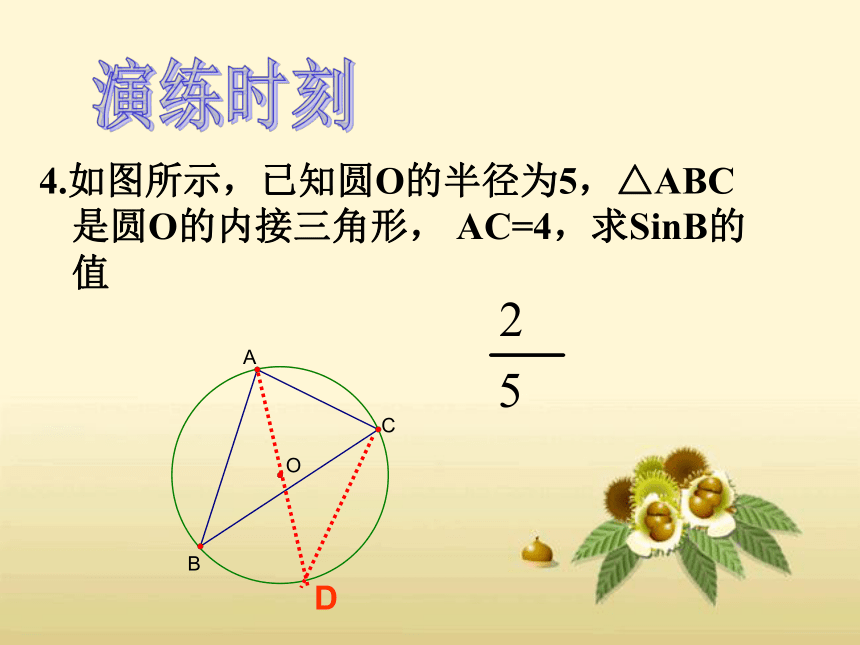
4.如图所示,已知圆O的半径为5,△ABC是圆O的内接三角形, AC=4,求SinB的值
D
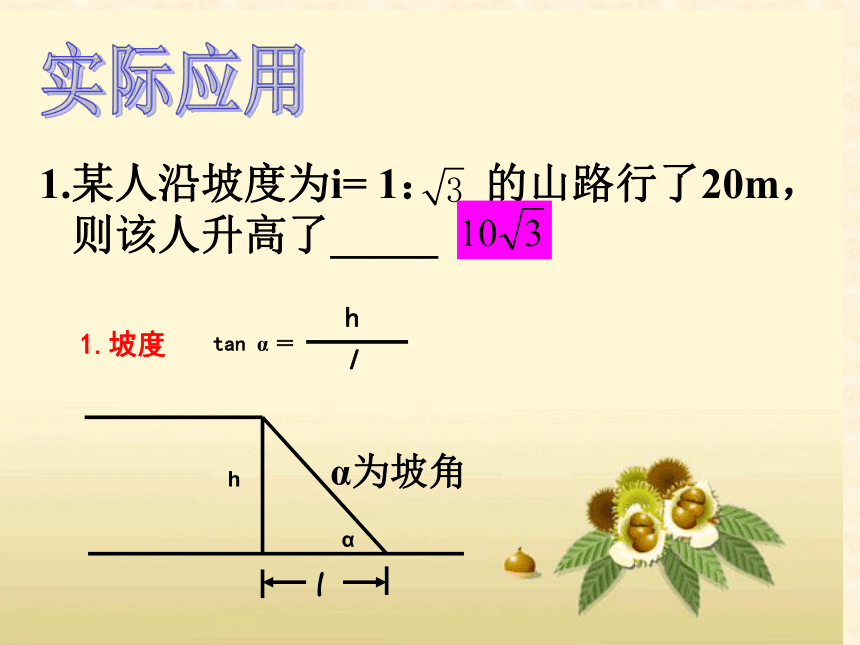
1.某人沿坡度为i= 1: 的山路行了20m,则该人升高了_____
l
h
α
1.坡度
tan α =
h
l
α为坡角
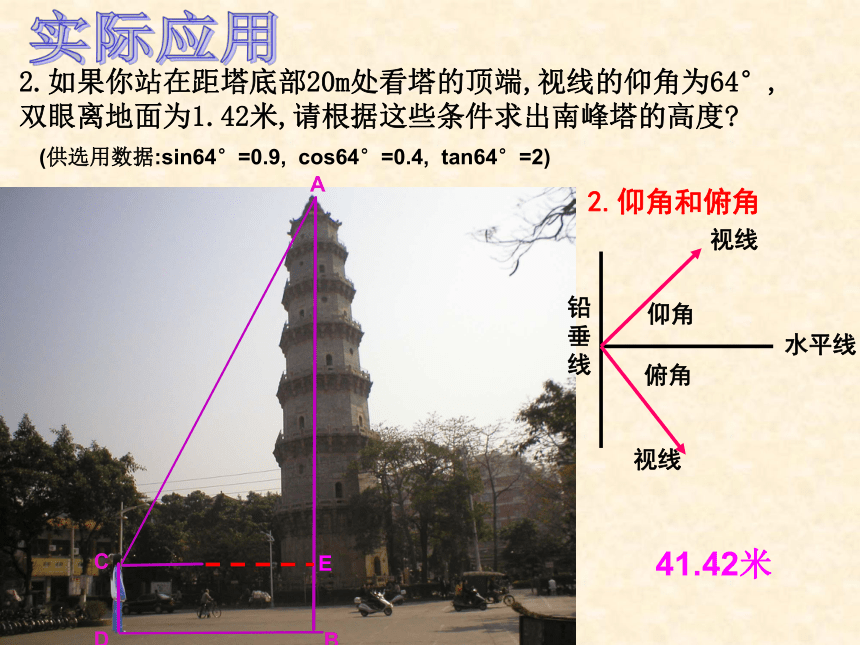
2.如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,请根据这些条件求出南峰塔的高度
A
B
C
D
(供选用数据:sin64°=0.9, cos64°=0.4, tan64°=2)
2.仰角和俯角
E
视线
铅垂线
水平线
视线
仰角
俯角
41.42米
3.如图,海上有一灯塔P,在它的周围6海里内有暗礁,一艘海轮以18海里/时的速度由西向东航行,行至点A处测得灯塔P在它的北偏东60°方向上,继续向东行驶20分后行至B处又测得灯塔P在它的北偏东45°方向上。如果海轮不改变方向继续前进,有没有触礁的危险?
(3)方位角
60°
45°
B
O
A
东
西
北
南
C
PC=
1.如图,楼顶有一根天线AB,为了测量天线的高度,在地面测量天线的高度,在地面测得楼顶B的仰角为45°,测得天线顶点A的仰角为60°,且点C到楼的距离CD为15m,求天线的长。
2.在地面上的A点测得树顶C的仰角为30°,沿着向树的方向前进6m到达B点,在B点测得树顶端C的仰角为45°
求出树高CD的长。(精确到0.1)
A
30°
45°
B
C
D
2.2米
3.如图,张华同学在学校某建筑物的点处测得旗杆顶部A点的仰角为30°,旗杆底部点B的俯角为45°.若旗杆底部B点到建筑物E的水平距离BE=9米,旗杆台阶高1米,则旗杆顶点离地面的高度为 米(结果保留根号).
1、通过以上习题学习以后,我们可以得到解直角三角形的两种基本图形:
小结:
2、注意可解直角三角形与非可解直角三角形的基本解题思路;
A
A
B
B
C
C
D
D
3、
现实对象
数学模型
实际问题的解
数学问题的解
数学抽象
逻辑推理
翻译回去
有无解?
1.如图,已知圆O的半径为1,AB=0.8.锐角三角形ABC内接于圆O,BD⊥AC于点D,OM⊥AB于M,则sin∠CBD的值______
0.6
某同学在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上。已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°。
问题:此时,A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC约为多少?(结果保留根号)
挑战自我
75
0
E
2.如图,为了测量河两案A、B两点的距离
在与AB垂直的方向点C处测得
AC=a,∠ACB=α,那么AB等于( )
A、a·sinα B、a·tanα C、a·cosα D、
A
B
C
a
α
B
3.如图,已知AB是半圆O的直径,弦AD,BC相交于点P,若∠DPB=α,则 等于( )
A.sinα B.cosα C.tanα D.
B
思 考
在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,∠ABC=30°,延长CB到D,连接AD使∠D=15°求tan15°的值。
D
A
C
B
如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,你能根据这些条件求出南峰塔的高度吗
一、基本概念
1.正弦
A
B
C
a
c
sinA=
2.余弦
b
cosA=
3.正切
tanA=
锐角A的正弦、余弦、正切、都叫做∠A的锐角三角函数.
定义:
练 习 1
如右图所示的Rt⊿ ABC中∠C=90°,a=5,b=12,
那么sinA= _____,
tanA = ______
cosB=______,
cosA=______ ,
一.锐角三角函数的概念:
tanα
cosα
sinα
6 0°
45 °
3 0°
角 度
三角函数
二、特殊角三角函数值
1
角度
逐渐
增大
正弦值如何变化
正弦值也增大
余弦值如何变化
余弦值逐渐减小
正切值如何变化
正切值也随之增大
思 考
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0
= 2
1.求下列各式的值
2sin30°+3tan30°+tan45°
cos245°+ tan60°cos30°
1.
2.
2.在△ABC中,∠C=90°,tanA= 则sinB=( )
D
3.在正方形网格中,的位置如图所示,则∠ B的正弦值为( )
问题:你能求∠ A的正弦吗?
B
4.如图所示,已知圆O的半径为5,△ABC是圆O的内接三角形, AC=4,求SinB的值
D
1.某人沿坡度为i= 1: 的山路行了20m,则该人升高了_____
l
h
α
1.坡度
tan α =
h
l
α为坡角
2.如果你站在距塔底部20m处看塔的顶端,视线的仰角为64°,
双眼离地面为1.42米,请根据这些条件求出南峰塔的高度
A
B
C
D
(供选用数据:sin64°=0.9, cos64°=0.4, tan64°=2)
2.仰角和俯角
E
视线
铅垂线
水平线
视线
仰角
俯角
41.42米
3.如图,海上有一灯塔P,在它的周围6海里内有暗礁,一艘海轮以18海里/时的速度由西向东航行,行至点A处测得灯塔P在它的北偏东60°方向上,继续向东行驶20分后行至B处又测得灯塔P在它的北偏东45°方向上。如果海轮不改变方向继续前进,有没有触礁的危险?
(3)方位角
60°
45°
B
O
A
东
西
北
南
C
PC=
1.如图,楼顶有一根天线AB,为了测量天线的高度,在地面测量天线的高度,在地面测得楼顶B的仰角为45°,测得天线顶点A的仰角为60°,且点C到楼的距离CD为15m,求天线的长。
2.在地面上的A点测得树顶C的仰角为30°,沿着向树的方向前进6m到达B点,在B点测得树顶端C的仰角为45°
求出树高CD的长。(精确到0.1)
A
30°
45°
B
C
D
2.2米
3.如图,张华同学在学校某建筑物的点处测得旗杆顶部A点的仰角为30°,旗杆底部点B的俯角为45°.若旗杆底部B点到建筑物E的水平距离BE=9米,旗杆台阶高1米,则旗杆顶点离地面的高度为 米(结果保留根号).
1、通过以上习题学习以后,我们可以得到解直角三角形的两种基本图形:
小结:
2、注意可解直角三角形与非可解直角三角形的基本解题思路;
A
A
B
B
C
C
D
D
3、
现实对象
数学模型
实际问题的解
数学问题的解
数学抽象
逻辑推理
翻译回去
有无解?
1.如图,已知圆O的半径为1,AB=0.8.锐角三角形ABC内接于圆O,BD⊥AC于点D,OM⊥AB于M,则sin∠CBD的值______
0.6
某同学在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上。已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°。
问题:此时,A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC约为多少?(结果保留根号)
挑战自我
75
0
E
2.如图,为了测量河两案A、B两点的距离
在与AB垂直的方向点C处测得
AC=a,∠ACB=α,那么AB等于( )
A、a·sinα B、a·tanα C、a·cosα D、
A
B
C
a
α
B
3.如图,已知AB是半圆O的直径,弦AD,BC相交于点P,若∠DPB=α,则 等于( )
A.sinα B.cosα C.tanα D.
B
思 考
在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,∠ABC=30°,延长CB到D,连接AD使∠D=15°求tan15°的值。
D
A
C
B
