浙教版九年级下册第3章直线与圆的位置关系复习
文档属性
| 名称 | 浙教版九年级下册第3章直线与圆的位置关系复习 |

|
|
| 格式 | rar | ||
| 文件大小 | 801.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-11 00:00:00 | ||
图片预览



文档简介
(共38张PPT)
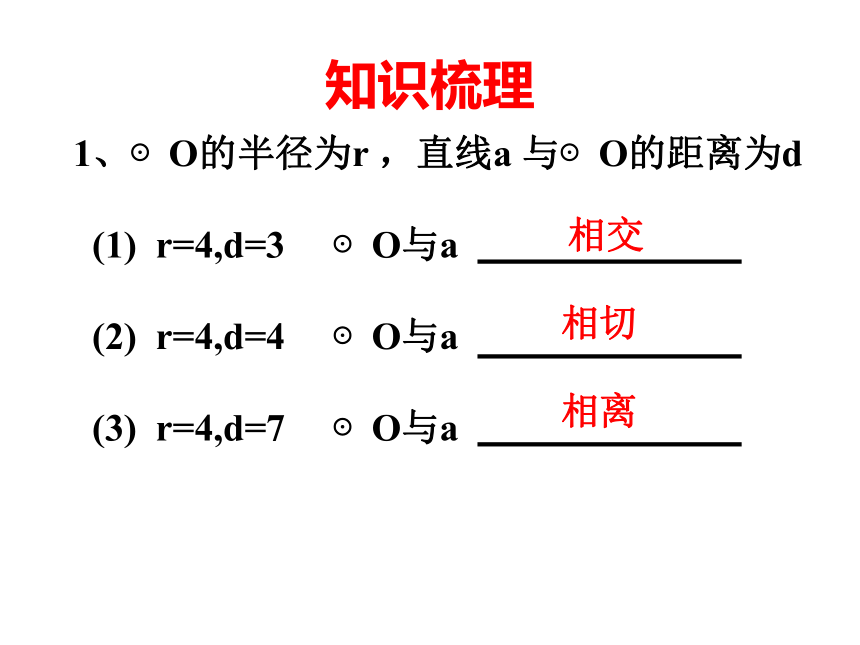
1、⊙O的半径为r ,直线a 与⊙O的距离为d
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
(3) r=4,d=7 ⊙O与a
相离
相交
相切
知识梳理
_
j
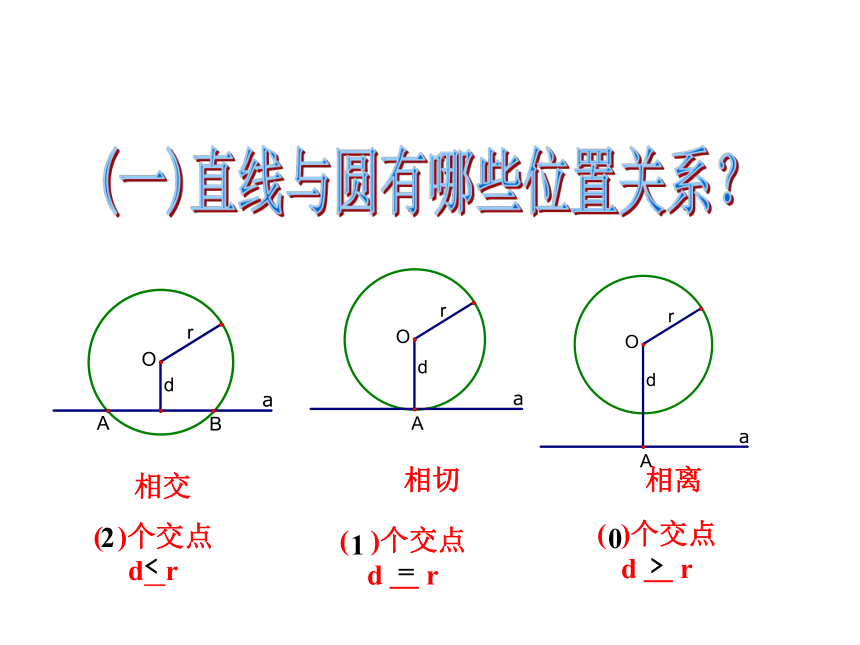
( )个交点
d _ r
( )个交点
d _ r
( )个交点
d r
2
﹤
1
=
0
﹥
相交
相切
相离
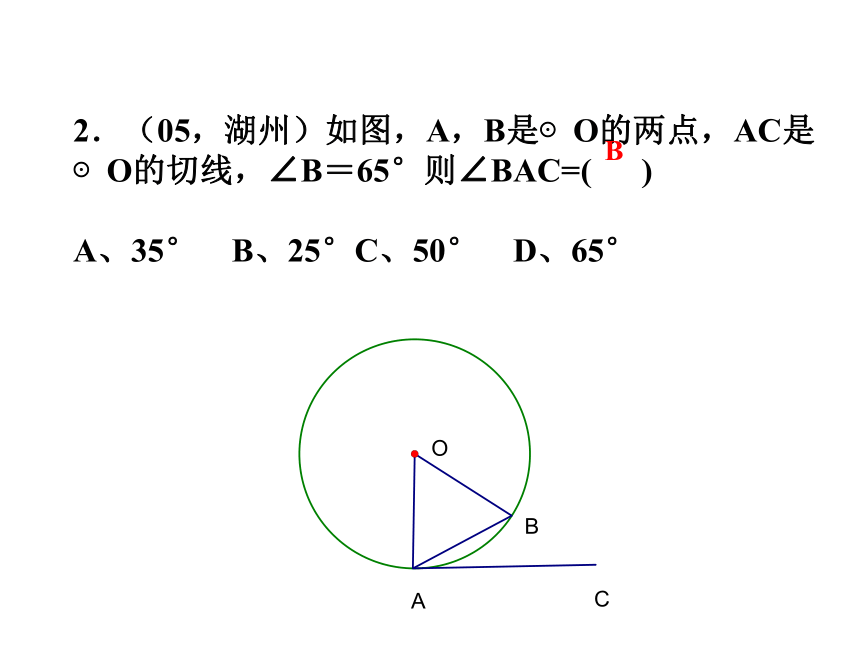
2.(05,湖州)如图,A,B是⊙O的两点,AC是⊙O的切线,∠B=65°则∠BAC=( )
A、35° B、25°C、50° D、65°
B
2.切线性质:
(1)切线垂直于过切点的直径
1.切线的判定:
(1)定义 直线与圆只有一个交点
(2)d=r 圆心到直线的距离等于半径
(3)直线过半径的外端并且垂直于这条半径
(2)d=r 圆心到直线的距离等于半径
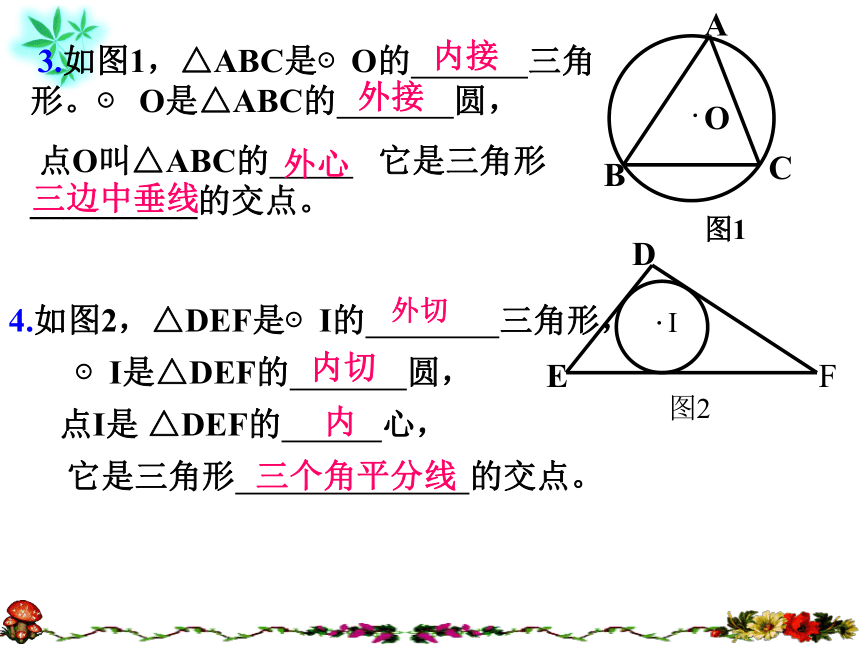
3.如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,
点O叫△ABC的 它是三角形 __________的交点。
外接
内接
外心
三边中垂线
4.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。
A
B
C
O
.
图1
I
D
E
F
.
图2
外切
内切
内
三个角平分线
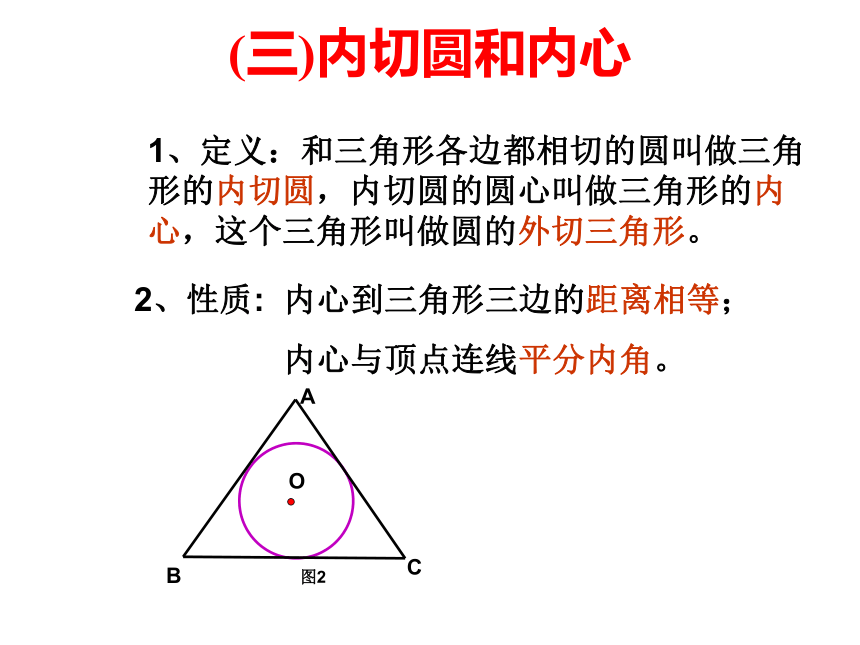
1、定义:和三角形各边都相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
2、性质: 内心到三角形三边的距离相等;
内心与顶点连线平分内角。
O
图2
A
B
C
(三)内切圆和内心
5.已知:⊙O1和⊙O2的半径分别2cm和4cm,当圆心距O1O2分别为下列数值时,判断两圆位置关系.
(1)2cm (2)4 cm (3) 6 cm
(4)0cm (5)8 cm (6) 1cm
外离
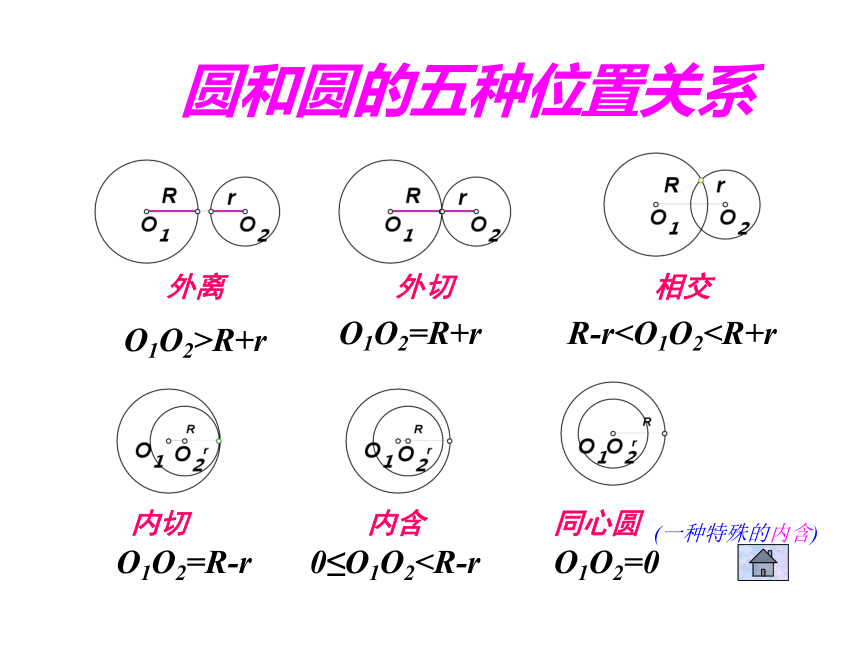
圆和圆的五种位置关系
O1O2>R+r
O1O2=R+r
R-rO1O2=R-r
0≤O1O2O1O2=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
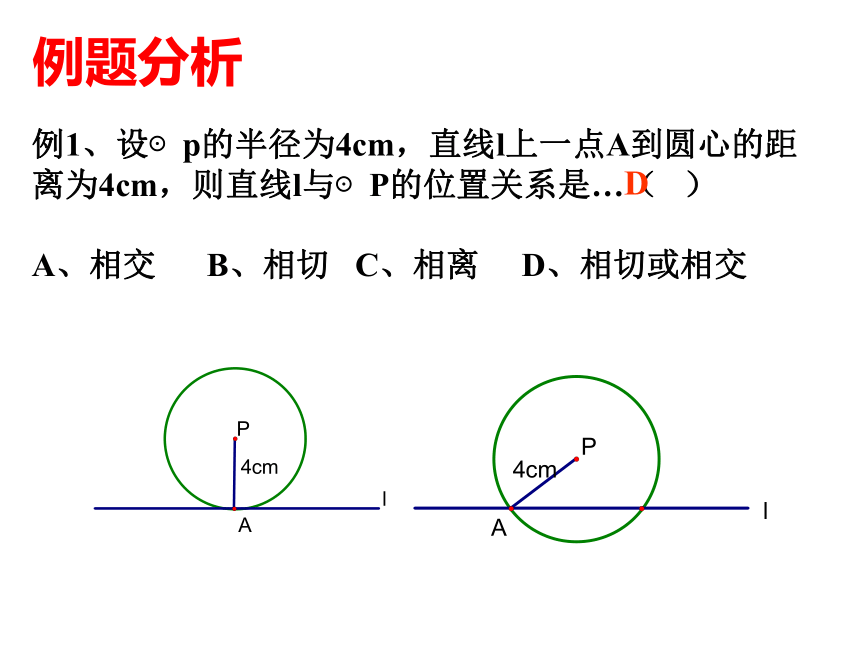
例1、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙P的位置关系是…( )
A、相交 B、相切 C、相离 D、相切或相交
D
例题分析
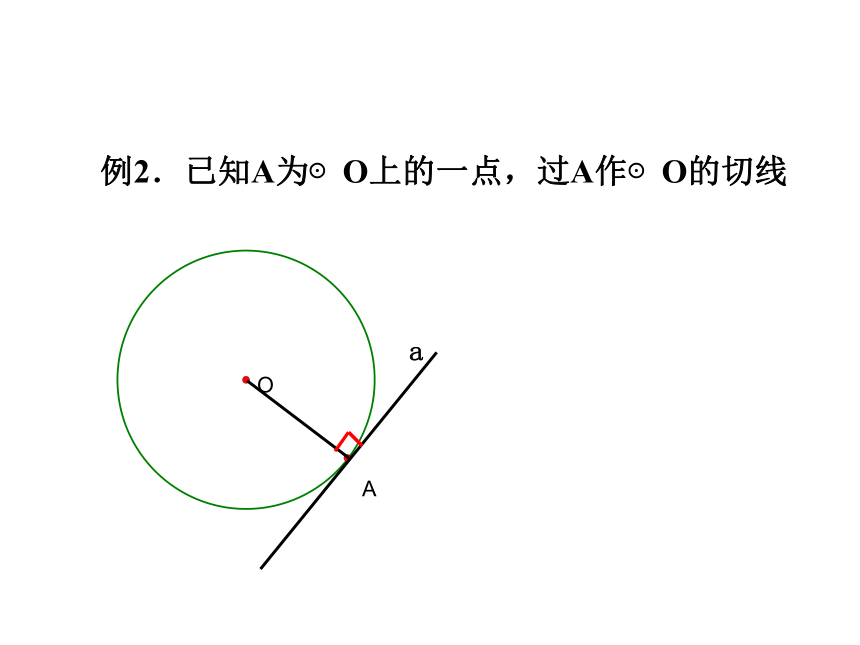
例2.已知A为⊙O上的一点,过A作⊙O的切线
a
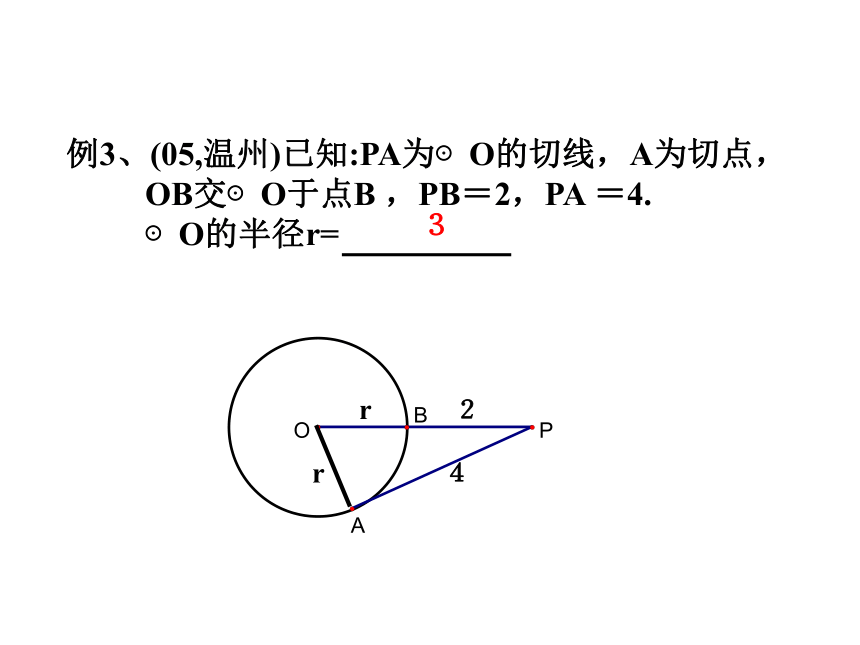
例3、(05,温州)已知:PA为⊙O的切线,A为切点,OB交⊙O于点B ,PB=2,PA =4.
⊙O的半径r=
2
4
r
r
3
例4、如图,AB是⊙O的直径,BC是⊙O的切线,AD∥CO,D是⊙O上的一点
(1)求证:△ADB∽△OBC ;
(2)若AB=2,∠C=300 ,求AD的长。
(1)证明:
∵ AB是⊙O的直径,
BC是⊙O的切线
∴ ∠D= ∠ABC=90°
又∵ AD∥CO
∴ ∠A= ∠COB
∴ △ADB∽△OBC
(2)
∵ △ADB∽△OBC,
∠ D =90°
∴ ∠C= ∠DBA=30°
∴AD= AB=1
课堂练习
1.如图,施工工地的水平地面上有三根外径都是1米的水泥管,两两相切地堆放在一起,则其最高点到地面的距离是 .
2.如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E.
由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
3、如图,园林部门准备在公园的三条小道围成的地块内建造一个圆形喷水池,要求面积尽量大。请问如何建造圆的面积最大?当圆的面积最大时,圆的半径是多少?
30m
40m
50m
A
B
C
O
r
4.在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,作EP⊥ED,交射线AB于点P,交射线CB于点F。
(1)如图,求证:△ADE∽△AEP;
(2)设OA=x,AP=y,求y关于x的函数解析式,并写出x的取值范围;
(3)当BF=1时,求线段AP的长.
(1)连结OD,∠A=∠A,∠ADE=∠AEP
(2)
(3)2或6
5 已知正三角形的边长为a,求它的内切圆与外接圆组成的圆环的面积.
解:设正三角形的外接圆、内切圆的半径分别为R,r,面积为S1、S2.
S= .
∵ ,
∴S= .
1、已知正方形的边长为a,求它的内切圆与外接圆组成的圆环的面积.
2、已知正五边形的边长为a,求它的内切圆与外接圆组成的圆环的面积.
3、通过例题及练习,你有什么发现?
你能说出这节课的收获和体验,让大家与你分享吗?
⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心,底边上
的高为半径的圆与底边相切。
1.是非题:判断下列命题是否正确。
(×)
(×)
(√)
(√)
(√)
作业题(第1题必做,其它选做)
2如图,如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB=
3.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A 16cm
D 8cm
C12cm
B 14cm
A
P
D
C
B
E
A
B
D
A
C
F
E
2
7
4
实验与操作:
4.分别以1厘米、2厘米、4厘米为半径,用圆规画圆,使他们两两外切。
5.如图1,分别表示边长为a的等边三角形和正方形,P表示直径为a的圆.图2是选择基本图形M.P用尺规画出的图案,
(1)写出图2的阴影部分的面积
(2)请你从图1中任意选择两种基本图形,按给定图形的大小设计一个新图案,还要选择恰当的图形部分涂上阴影,并计算阴影的面积;(尺规作图,不写作法,保留痕迹,作直角时可以使用三角板)
(3)请你写一句在完成本题的过程中感受较深且与数学有关的话.
图2
M
N
图1
P
最好的应用数学是与最好的纯数学同样深奥、美妙和有趣.
在生活中体验数学,用数学解释生活.
下课了!
一种圆管的横截面是同心圆的圆环面,用刻度尺,只测量圆管横截面的哪一条弦的大小,就可以算出截面的面积?
A
B
C
D
E
O
1.正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系。圆心为A(3,0)的⊙A被y轴截得的弦长BC=8,如图11所示。解答下列问题:
(1)⊙A的半径为_____;
(2)请在图中将⊙A先向上平移6个单位,再向左平移8个单位得到⊙D,观察你所画的图形知⊙D的圆心D点的坐标是_____;⊙D与x轴的位置关系是____;⊙D与y轴的位置关系是_____;⊙D与⊙A的位置关系是_______。
(3)画出以点E(—8,0)为位似中心,将⊙D缩小为原来的的⊙F
(1)5 (2)(-5,6)相离,相切,外切 (3)略
2.如图,AD、AE分别是⊙O的切线,D、E为切点,BC切⊙O于F,交AD、AE于点B、C,若AD=8.则三角形ABC的周长是( )
A. 8 B.10 C.16 D.不能确定
3.如图,△ABC中,∠BCA=90°,∠A=30°,以AB为直径画⊙O,延长AB到D,使BD等于⊙O的半径.
求证:CD是⊙O的切线.
求不规则图形面积时,要认真观察图形,准确分解与组合,化归为常见的基本图形。
现在假如诗人的视力非常非常好,他能看到很远很远的
地方,那么他要登上几层楼高,才能看见千里以外的景物
∠O= =
∴
≈4.5°
解:依题意AB为最小楼高,AC切圆0于C
如图:地球上B.C两点间的距离指的是球面上两点间的距离,它就是弧BC的长,假设弧BC的长是500千米(即1000里),OB=6400(千米,近似数),求高度AB
O
实践出真知
A
C
B
(温馨提示:tan4.5°=0.079 cos4.5°=0.997
tan6.2°=0.109 cos6.2°=0.994
弧长公式 L= π取3.14,精确到0.1km)
∵L=
在Rt⊿ACO中
AO=OC/ cos4.5°=6400÷0.997
=6419.26
∴AB=6419.26-6400≈19.3(Km)
相当于珠穆朗玛峰高度的2倍多!
5000层楼高呀,是目前世界上最高楼
----马来西亚的双叶大厦的50倍!
例1 如图,已知半径OA=6cm,C为OB的中点,∠AOB=120°,求阴影部分的面积.
如图:把直角三角形ABC的斜边AB放在定直线L上,按时针方向在L上转动两次,使它转到△A”B”C”的位置,设BC=1,AC=√3,则顶点A运动到A”的位置时,点A经过的路线与直线L所围成的面积是 (计算结果不取近似值)
A
B
C
A`
A”
C”
B”
提高练习
从一个底面半径为40cm,高60cm的圆柱中挖去一个以圆柱上底为底,下底圆心为顶点的圆锥,如图,得到一个几何体,求这个几何体的表面积。
水平放着的圆柱形水管的截面半径是0.6m,其中水面高是0.3m。求截面上有水的弓形的面积(精确到0.01m2)
如图,⊙O的半径为R,直径AB⊥CD,以B为圆心,以BC为半径作弧CED。求弧CED与弧CAD围成的新月形ACED的面积S。
1、⊙O的半径为r ,直线a 与⊙O的距离为d
(1) r=4,d=3 ⊙O与a
(2) r=4,d=4 ⊙O与a
(3) r=4,d=7 ⊙O与a
相离
相交
相切
知识梳理
_
j
( )个交点
d _ r
( )个交点
d _ r
( )个交点
d r
2
﹤
1
=
0
﹥
相交
相切
相离
2.(05,湖州)如图,A,B是⊙O的两点,AC是⊙O的切线,∠B=65°则∠BAC=( )
A、35° B、25°C、50° D、65°
B
2.切线性质:
(1)切线垂直于过切点的直径
1.切线的判定:
(1)定义 直线与圆只有一个交点
(2)d=r 圆心到直线的距离等于半径
(3)直线过半径的外端并且垂直于这条半径
(2)d=r 圆心到直线的距离等于半径
3.如图1,△ABC是⊙O的 三角形。⊙ O是△ABC的 圆,
点O叫△ABC的 它是三角形 __________的交点。
外接
内接
外心
三边中垂线
4.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点。
A
B
C
O
.
图1
I
D
E
F
.
图2
外切
内切
内
三个角平分线
1、定义:和三角形各边都相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
2、性质: 内心到三角形三边的距离相等;
内心与顶点连线平分内角。
O
图2
A
B
C
(三)内切圆和内心
5.已知:⊙O1和⊙O2的半径分别2cm和4cm,当圆心距O1O2分别为下列数值时,判断两圆位置关系.
(1)2cm (2)4 cm (3) 6 cm
(4)0cm (5)8 cm (6) 1cm
外离
圆和圆的五种位置关系
O1O2>R+r
O1O2=R+r
R-r
0≤O1O2
外切
相交
内切
内含
同心圆
(一种特殊的内含)
例1、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙P的位置关系是…( )
A、相交 B、相切 C、相离 D、相切或相交
D
例题分析
例2.已知A为⊙O上的一点,过A作⊙O的切线
a
例3、(05,温州)已知:PA为⊙O的切线,A为切点,OB交⊙O于点B ,PB=2,PA =4.
⊙O的半径r=
2
4
r
r
3
例4、如图,AB是⊙O的直径,BC是⊙O的切线,AD∥CO,D是⊙O上的一点
(1)求证:△ADB∽△OBC ;
(2)若AB=2,∠C=300 ,求AD的长。
(1)证明:
∵ AB是⊙O的直径,
BC是⊙O的切线
∴ ∠D= ∠ABC=90°
又∵ AD∥CO
∴ ∠A= ∠COB
∴ △ADB∽△OBC
(2)
∵ △ADB∽△OBC,
∠ D =90°
∴ ∠C= ∠DBA=30°
∴AD= AB=1
课堂练习
1.如图,施工工地的水平地面上有三根外径都是1米的水泥管,两两相切地堆放在一起,则其最高点到地面的距离是 .
2.如图,AB是⊙O的直径,⊙O过AC的中点D ,DE⊥BC ,垂足为E.
由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
3、如图,园林部门准备在公园的三条小道围成的地块内建造一个圆形喷水池,要求面积尽量大。请问如何建造圆的面积最大?当圆的面积最大时,圆的半径是多少?
30m
40m
50m
A
B
C
O
r
4.在△ABC中,∠ABC=90°,AB=4,BC=3,O是边AC上的一个动点,以点O为圆心作半圆,与边AB相切于点D,交线段OC于点E,作EP⊥ED,交射线AB于点P,交射线CB于点F。
(1)如图,求证:△ADE∽△AEP;
(2)设OA=x,AP=y,求y关于x的函数解析式,并写出x的取值范围;
(3)当BF=1时,求线段AP的长.
(1)连结OD,∠A=∠A,∠ADE=∠AEP
(2)
(3)2或6
5 已知正三角形的边长为a,求它的内切圆与外接圆组成的圆环的面积.
解:设正三角形的外接圆、内切圆的半径分别为R,r,面积为S1、S2.
S= .
∵ ,
∴S= .
1、已知正方形的边长为a,求它的内切圆与外接圆组成的圆环的面积.
2、已知正五边形的边长为a,求它的内切圆与外接圆组成的圆环的面积.
3、通过例题及练习,你有什么发现?
你能说出这节课的收获和体验,让大家与你分享吗?
⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心,底边上
的高为半径的圆与底边相切。
1.是非题:判断下列命题是否正确。
(×)
(×)
(√)
(√)
(√)
作业题(第1题必做,其它选做)
2如图,如果AF=2cm,BD=7cm,CE=4cm,则BC= cm,AC= AB=
3.如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则Δ PDE的周长为( )
A 16cm
D 8cm
C12cm
B 14cm
A
P
D
C
B
E
A
B
D
A
C
F
E
2
7
4
实验与操作:
4.分别以1厘米、2厘米、4厘米为半径,用圆规画圆,使他们两两外切。
5.如图1,分别表示边长为a的等边三角形和正方形,P表示直径为a的圆.图2是选择基本图形M.P用尺规画出的图案,
(1)写出图2的阴影部分的面积
(2)请你从图1中任意选择两种基本图形,按给定图形的大小设计一个新图案,还要选择恰当的图形部分涂上阴影,并计算阴影的面积;(尺规作图,不写作法,保留痕迹,作直角时可以使用三角板)
(3)请你写一句在完成本题的过程中感受较深且与数学有关的话.
图2
M
N
图1
P
最好的应用数学是与最好的纯数学同样深奥、美妙和有趣.
在生活中体验数学,用数学解释生活.
下课了!
一种圆管的横截面是同心圆的圆环面,用刻度尺,只测量圆管横截面的哪一条弦的大小,就可以算出截面的面积?
A
B
C
D
E
O
1.正方形网格中,每个小正方形的边长为1个单位,以O为原点建立平面直角坐标系。圆心为A(3,0)的⊙A被y轴截得的弦长BC=8,如图11所示。解答下列问题:
(1)⊙A的半径为_____;
(2)请在图中将⊙A先向上平移6个单位,再向左平移8个单位得到⊙D,观察你所画的图形知⊙D的圆心D点的坐标是_____;⊙D与x轴的位置关系是____;⊙D与y轴的位置关系是_____;⊙D与⊙A的位置关系是_______。
(3)画出以点E(—8,0)为位似中心,将⊙D缩小为原来的的⊙F
(1)5 (2)(-5,6)相离,相切,外切 (3)略
2.如图,AD、AE分别是⊙O的切线,D、E为切点,BC切⊙O于F,交AD、AE于点B、C,若AD=8.则三角形ABC的周长是( )
A. 8 B.10 C.16 D.不能确定
3.如图,△ABC中,∠BCA=90°,∠A=30°,以AB为直径画⊙O,延长AB到D,使BD等于⊙O的半径.
求证:CD是⊙O的切线.
求不规则图形面积时,要认真观察图形,准确分解与组合,化归为常见的基本图形。
现在假如诗人的视力非常非常好,他能看到很远很远的
地方,那么他要登上几层楼高,才能看见千里以外的景物
∠O= =
∴
≈4.5°
解:依题意AB为最小楼高,AC切圆0于C
如图:地球上B.C两点间的距离指的是球面上两点间的距离,它就是弧BC的长,假设弧BC的长是500千米(即1000里),OB=6400(千米,近似数),求高度AB
O
实践出真知
A
C
B
(温馨提示:tan4.5°=0.079 cos4.5°=0.997
tan6.2°=0.109 cos6.2°=0.994
弧长公式 L= π取3.14,精确到0.1km)
∵L=
在Rt⊿ACO中
AO=OC/ cos4.5°=6400÷0.997
=6419.26
∴AB=6419.26-6400≈19.3(Km)
相当于珠穆朗玛峰高度的2倍多!
5000层楼高呀,是目前世界上最高楼
----马来西亚的双叶大厦的50倍!
例1 如图,已知半径OA=6cm,C为OB的中点,∠AOB=120°,求阴影部分的面积.
如图:把直角三角形ABC的斜边AB放在定直线L上,按时针方向在L上转动两次,使它转到△A”B”C”的位置,设BC=1,AC=√3,则顶点A运动到A”的位置时,点A经过的路线与直线L所围成的面积是 (计算结果不取近似值)
A
B
C
A`
A”
C”
B”
提高练习
从一个底面半径为40cm,高60cm的圆柱中挖去一个以圆柱上底为底,下底圆心为顶点的圆锥,如图,得到一个几何体,求这个几何体的表面积。
水平放着的圆柱形水管的截面半径是0.6m,其中水面高是0.3m。求截面上有水的弓形的面积(精确到0.01m2)
如图,⊙O的半径为R,直径AB⊥CD,以B为圆心,以BC为半径作弧CED。求弧CED与弧CAD围成的新月形ACED的面积S。
