直线与圆的位置复习课
图片预览



文档简介
(共15张PPT)
下雨天当你快速转动雨伞时飞出的水,沿着圆的切线的方向飞出的.
问题:
当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
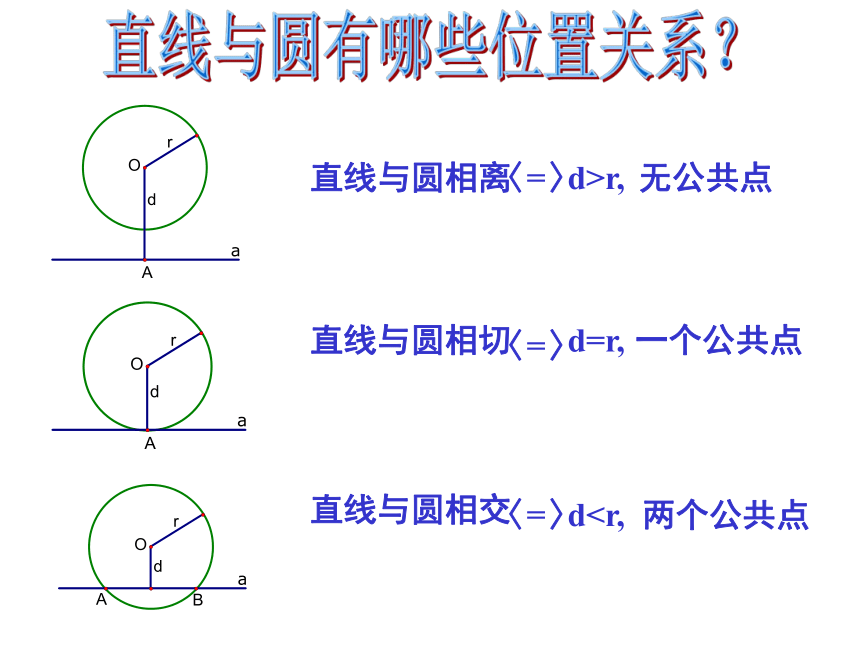
直线与圆相交
直线与圆相切
直线与圆相离
一个公共点
d=r,
〈=〉
两个公共点
d〈=〉
无公共点
d>r,
〈=〉
a
r
A
O
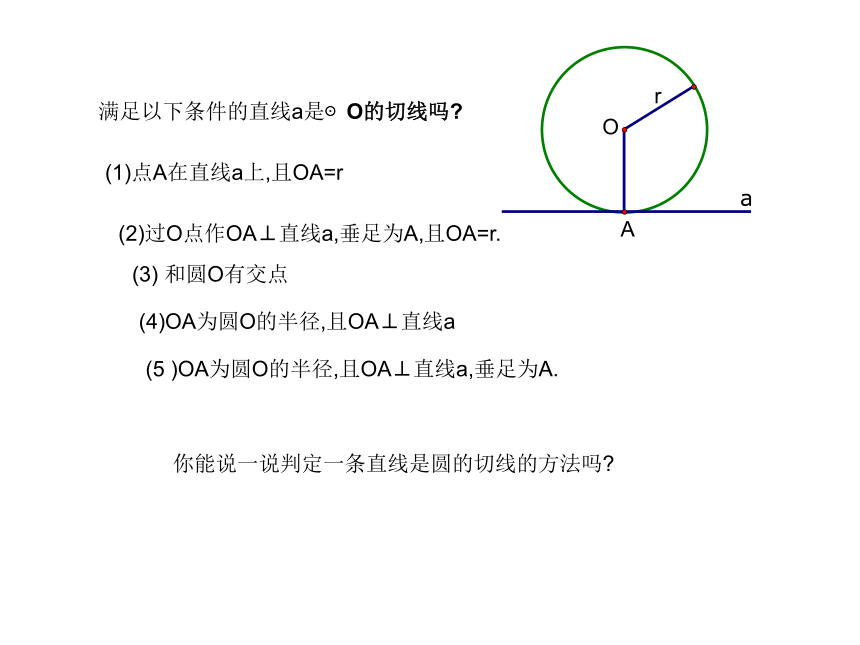
满足以下条件的直线a是⊙O的切线吗
(1)点A在直线a上,且OA=r
(2)过O点作OA⊥直线a,垂足为A,且OA=r.
(3) 和圆O有交点
(4)OA为圆O的半径,且OA⊥直线a
(5 )OA为圆O的半径,且OA⊥直线a,垂足为A.
你能说一说判定一条直线是圆的切线的方法吗
切点
切线
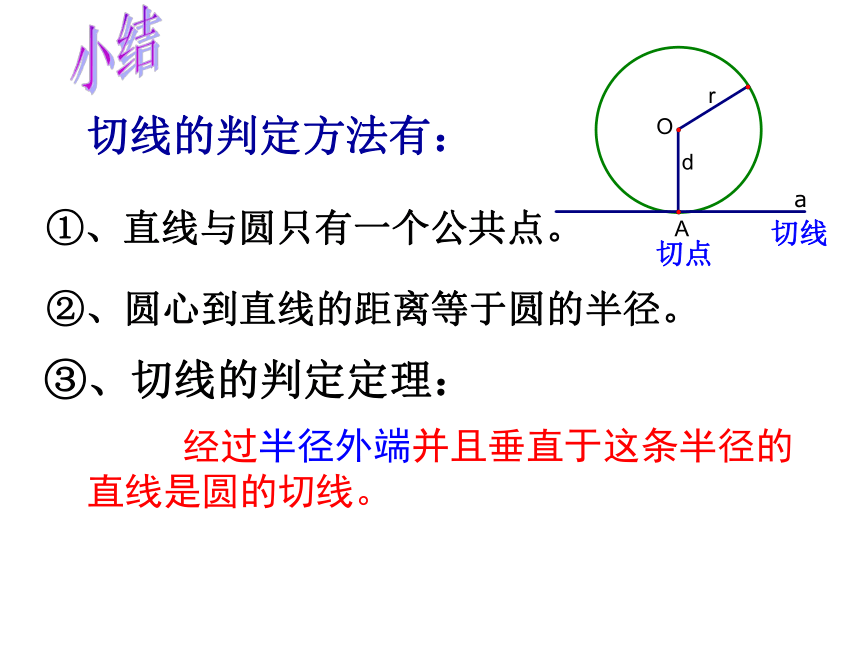
切线的判定方法有:
③、切线的判定定理:
②、圆心到直线的距离等于圆的半径。
①、直线与圆只有一个公共点。
经过半径外端并且垂直于这条半径的直线是圆的切线。
1、如果直线a与⊙O有公共点,那么直线a与⊙O的位置关系为_____________
2、正△ABC的边长为1cm,以点A为圆心,半径为r的圆与BC相切,则r=_________
相切或相交
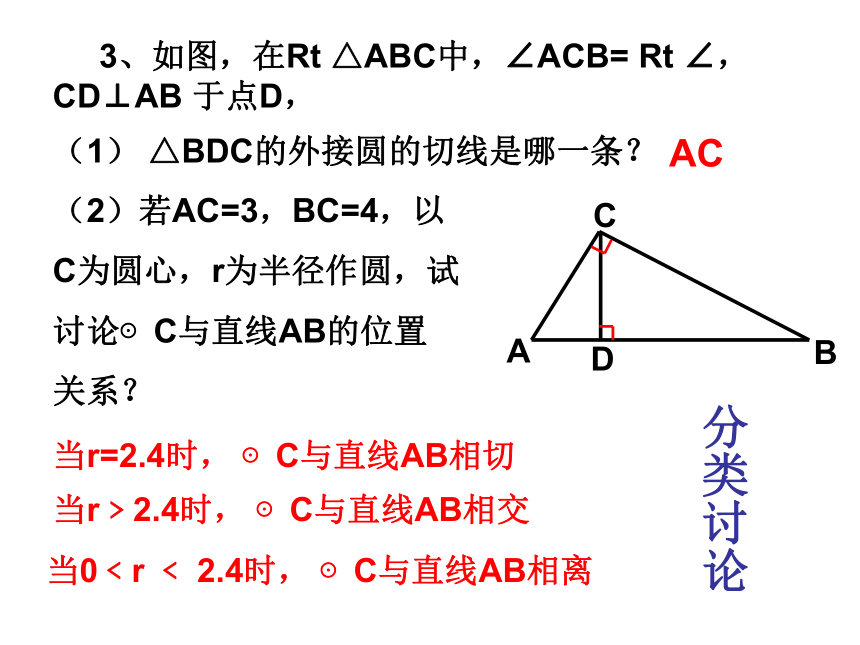
3、如图,在Rt △ABC中,∠ACB= Rt ∠,CD⊥AB 于点D,
(1) △BDC的外接圆的切线是哪一条?
(2)若AC=3,BC=4,以
C为圆心,r为半径作圆,试
讨论⊙C与直线AB的位置
关系?
A
B
C
D
AC
当r=2.4时, ⊙C与直线AB相切
当r﹥2.4时, ⊙C与直线AB相交
当0﹤r ﹤ 2.4时, ⊙C与直线AB相离
分类讨论
议一议
你能说一说切线的性质吗
切点.垂直.圆心
1、如图,AB是⊙O的切线,A为切点,若OP=13,OB=5,则AP=______
A
P
.
B
O
2、如图,BC切⊙O于点C, BC⊥AC交⊙O于点A,AB交⊙O于点E,已知∠A=30°,BC= ,则⊙O的直径为____
.
A
C
B
E
O
3
12
经过切点的半径垂直于圆的切线
经过切点垂直于切线的直线必经过圆心.
切线的性质
1、如图,AB是⊙O的切线, A为切点,AC是 ⊙O 的弦,过 O作OH⊥AC于点H,若OH=2,AB=12,BO=13,则 ⊙O 的半径为_____,sin ∠OAC=_____,弦AC的长为_____
5
5
2
.
A
C
B
H
O
2、 ⊙O是△ABC的内切圆,切点分别为P、E、F,若∠B= 60°, ∠C= 40°,则∠PFE=_______
3、如图, ⊙O的直径AB=6cm,D为⊙O上一点, ∠BAD= 30°,过点D的切线交AB的延长线于点C,则∠ADC=_____, AC=______.
O
.
P
E
F
A
B
C
.
D
A
B
O
C
50°
120°
9
解题中常用辅助线的添法:连结切点与圆心
如图,AB是⊙O的直径,D是⊙O上一动点,延长AD到C,使CD=AD, 过D作DE⊥BC ,垂足为E.
由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
D
E
O
B
A
C
D
E
C
O
B
A
如图,AB是⊙O的直径,D是⊙O上一动点,延长AD到C,使CD=AD, 过D作DE⊥BC ,垂足为E.
(1)AD的长度为x,BD的长度为y,用 含x的代数式表示y
连结BD,设⊙O的半径为2
(2)BC与⊙O是否有可能相切?若不可能相切,则说明理由,若能相切,则指出x为何值时相切?
⌒
并求出此时DE的长及由DE,BE和弧DB所围成的阴影部分的面积?
知识与技能:
1.直线与圆的三种位置关系:相交、相切、相离
2.直线与圆相切的判定与性质
数学思想方法:
分类讨论 数形结合
下雨天当你快速转动雨伞时飞出的水,沿着圆的切线的方向飞出的.
问题:
当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
直线与圆相交
直线与圆相切
直线与圆相离
一个公共点
d=r,
〈=〉
两个公共点
d
无公共点
d>r,
〈=〉
a
r
A
O
满足以下条件的直线a是⊙O的切线吗
(1)点A在直线a上,且OA=r
(2)过O点作OA⊥直线a,垂足为A,且OA=r.
(3) 和圆O有交点
(4)OA为圆O的半径,且OA⊥直线a
(5 )OA为圆O的半径,且OA⊥直线a,垂足为A.
你能说一说判定一条直线是圆的切线的方法吗
切点
切线
切线的判定方法有:
③、切线的判定定理:
②、圆心到直线的距离等于圆的半径。
①、直线与圆只有一个公共点。
经过半径外端并且垂直于这条半径的直线是圆的切线。
1、如果直线a与⊙O有公共点,那么直线a与⊙O的位置关系为_____________
2、正△ABC的边长为1cm,以点A为圆心,半径为r的圆与BC相切,则r=_________
相切或相交
3、如图,在Rt △ABC中,∠ACB= Rt ∠,CD⊥AB 于点D,
(1) △BDC的外接圆的切线是哪一条?
(2)若AC=3,BC=4,以
C为圆心,r为半径作圆,试
讨论⊙C与直线AB的位置
关系?
A
B
C
D
AC
当r=2.4时, ⊙C与直线AB相切
当r﹥2.4时, ⊙C与直线AB相交
当0﹤r ﹤ 2.4时, ⊙C与直线AB相离
分类讨论
议一议
你能说一说切线的性质吗
切点.垂直.圆心
1、如图,AB是⊙O的切线,A为切点,若OP=13,OB=5,则AP=______
A
P
.
B
O
2、如图,BC切⊙O于点C, BC⊥AC交⊙O于点A,AB交⊙O于点E,已知∠A=30°,BC= ,则⊙O的直径为____
.
A
C
B
E
O
3
12
经过切点的半径垂直于圆的切线
经过切点垂直于切线的直线必经过圆心.
切线的性质
1、如图,AB是⊙O的切线, A为切点,AC是 ⊙O 的弦,过 O作OH⊥AC于点H,若OH=2,AB=12,BO=13,则 ⊙O 的半径为_____,sin ∠OAC=_____,弦AC的长为_____
5
5
2
.
A
C
B
H
O
2、 ⊙O是△ABC的内切圆,切点分别为P、E、F,若∠B= 60°, ∠C= 40°,则∠PFE=_______
3、如图, ⊙O的直径AB=6cm,D为⊙O上一点, ∠BAD= 30°,过点D的切线交AB的延长线于点C,则∠ADC=_____, AC=______.
O
.
P
E
F
A
B
C
.
D
A
B
O
C
50°
120°
9
解题中常用辅助线的添法:连结切点与圆心
如图,AB是⊙O的直径,D是⊙O上一动点,延长AD到C,使CD=AD, 过D作DE⊥BC ,垂足为E.
由以上条件,你能推出哪些结论(至少2个)?说明理由(要求:不再标注其他字母,寻找过程中所添加的辅助线不能出现在结论中)
D
E
O
B
A
C
D
E
C
O
B
A
如图,AB是⊙O的直径,D是⊙O上一动点,延长AD到C,使CD=AD, 过D作DE⊥BC ,垂足为E.
(1)AD的长度为x,BD的长度为y,用 含x的代数式表示y
连结BD,设⊙O的半径为2
(2)BC与⊙O是否有可能相切?若不可能相切,则说明理由,若能相切,则指出x为何值时相切?
⌒
并求出此时DE的长及由DE,BE和弧DB所围成的阴影部分的面积?
知识与技能:
1.直线与圆的三种位置关系:相交、相切、相离
2.直线与圆相切的判定与性质
数学思想方法:
分类讨论 数形结合
