一元二次方程复习(1)

(共47张PPT)
第二章 一元二次方程复习（1）
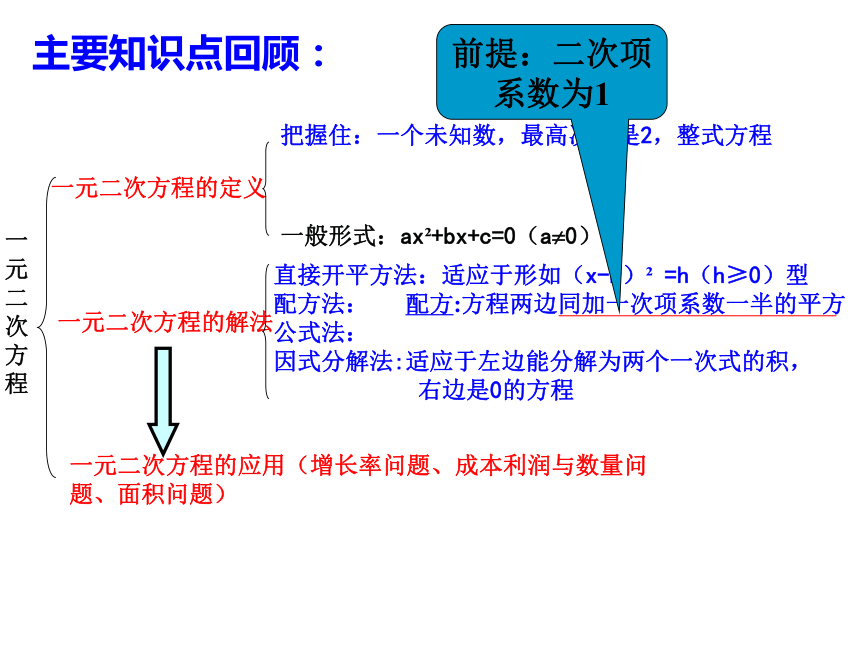
主要知识点回顾：
一
元
二
次
方
程
一元二次方程的定义
一元二次方程的解法
一元二次方程的应用（增长率问题、成本利润与数量问题、面积问题）
把握住：一个未知数，最高次数是2，整式方程
一般形式：ax +bx+c=0（a 0）
直接开平方法：适应于形如（x-k） =h（h≥0）型
配方法： 配方:方程两边同加一次项系数一半的平方
公式法：
因式分解法:适应于左边能分解为两个一次式的积，
右边是0的方程
前提：二次项系数为1
一元二次方程的概念：
1.（07兰州）下列方程中是一元二次方程的是（ ）
A、2x＋1＝0 B、y2＋x＝1
C、x2＋1＝0 D、
C
2.（08青岛）关于x的方程 是一元二次方程，求m的值。
一元二次方程三要素:
1.一个未知数.
2.含未知项的最高次数是2次.
3.方程两边都是整式.
二次项的系数不等于0.
注意:
m=-2
1、关于y的一元二次方程2y(y-3)= -4的一般形式是 ,它的二次项系数是 ,一次项是 , 常数项是 ；
做一做
一元二次方程的一般形式：
4
2y2-6y+4=0
-6y
2
一元二次方程的解法
直接开平方法
因式分解法
配方法
公式法
练一练
1、用指定的方法解下列方程：
——直接开平方法
——配方法
——公式法
——因式分解法
——因式分解法
例3、请选择最好的方法求解下列方程
1.（3x -2） -49=0 3.（3x -4） =（4x -3）
2.4y = 1 - y
解： （3x-2） =49
3x -2=±7
x=
x1=3，x2= -
解：（3x-4） -（4x-3） =0 （3x-4+4x-3）（3x-4x+3）=0
（7x-7）（-x-1）=0
7x-7=0或-x-1=0
x1 = -1， x2 =1
解：3y +8y -2=0
b - 4ac=64 -4 3 （-2）=88
y=
请你选择恰当的方法解方程:　
①　(x-1)(x+1)=x
②　x (2x+5)=2 (2x+5)
③　(2x－1)2=4(x+3)2
④　3(x-2)2－9=0
⑤
1、用配方法解方程2x +4x +1 =0，配方后得到的方程是 。
2、一元二次方程ax +bx +c =0，若x=1是它的一个根，则a+b+c= ，若a-b+c=0，则方程必有一根为 。
4、方程2x -mx-m =0有一个根为–1,则m= ，另一个根为 。
0
5或-1。
2或-1
2或1/2
-1
5、若x2+6x+m=（x+n)2,则m= ,n= .
（x+1） =
9
3
填一填
阅读材料，解答问题
问题：1、在由原方程得到方程（1）的过程中，利用了 ， 法达到了降次的目的，体现了 的数学思想。
为了解方程（y -1） -3（y -1）+2=0，我们将y -1视为一个整体，解：设 y -1=a，则（y -1） =a ，
a - 3a+2=0， （1） a1=1，a2=2。
当a=1时，y -1=1，y =± ，
当a=2时，y -1=2，y=±
所以y1= ，y2 =- y 3= y4= -
换元
转化
用上述方法解下列方程：
一元二次方程根的判别式
两不相等实根
两相等实根
无实根
一元二次方程
一元二次方程 根的判式是:
判别式的情况
根的情况
定理与逆定理
两个不相等实根
两个相等实根
无实根(无解)
知识聚焦
例1：不解方程，判别下列方程的根的情况
（1）
（3）
（2）
解：（1） =
所以，原方程有两个不相等的实根。
说明：解这类题目时，一般要先把方程化为一般形式，求出△，然后对△进行计算，使△的符号明朗化，进而说明△的符号情况，得出结论。
例2：当k取什么值时，已知关于x的方程：
（1）方程有两个不相等的实根；
（2）方程有两个相等的实根；（3）方程无实根；
解：△=
(1).当△>0 ，方程有两个不相等的实根, 8k+9 >0 , 即
(2).当△ = 0 ，方程有两个相等的实根, 8k+9 =0 , 即
说明：解此类题目时，也是先把方程化为一般形式，再算出△，再由题目给出的根的情况确定△的情况。从而求出待定系数的取值范围
(3).当△ <0 ，方程有没有实数根, 8k+9 <0 , 即
K＜
例3、已知m为非负整数，且关于x的方程 ：
有两个实数根，求m的值。
解：∵方程有两个实数根
∴
解得：
∵m为非负数
∴m=0或m=1
说明：当二次项系数也含有待定的字母时，要注意二次项系数不能为0，还要注意题目中待定字母的取值范围.
例4、求证：关于x的方程：
有两个不相等的实根。
证明：
所以，无论m取任何实数,方程有两个不相等的实数根。
无论m取任何实数都有：
即：△>0
说明：此类题目要先把方程化成一般形式，再计算出△，如果不能直接判断△情况，就利用配方法把△配成含用完全平方的形式，根据完全平方的非负性，判断△的情况，从而证明出方程根的情况.
2、求证：
（1）对于任何实数x，均有： ＞0；
（2）不论x为何实数，多项式 的值总 大于 的值。
1、已知关于x的一元二次方程x2-2(k-1)x+k2-2=0有实数根,求k的取值范围
练一练
3、方程ｘ2－２ｘ＋２＝０的根的情况是（　　）
（Ａ）只有一个实数根　　（Ｂ）有两个不相等的实数根
（Ｃ）有两个相等的实数根　（Ｄ）没有实数根0
D
4、有一边长为３的等腰三角形，它的两边长是方程ｘ2－４ｘ＋ｋ＝０的两根，求这个三角形的周长？　
练一练