2.3一元二次方程的应用(1)
图片预览





文档简介
(共16张PPT)
金陵路商业街某花店,如果每束玫瑰盈利10元,平均每天可售出40束.为扩大销售,经调查发现,若每束降价1元,则平均每天可多售出8束.如果花店每天要盈利432元, 那么每束玫瑰应降价多少元
生活情境一
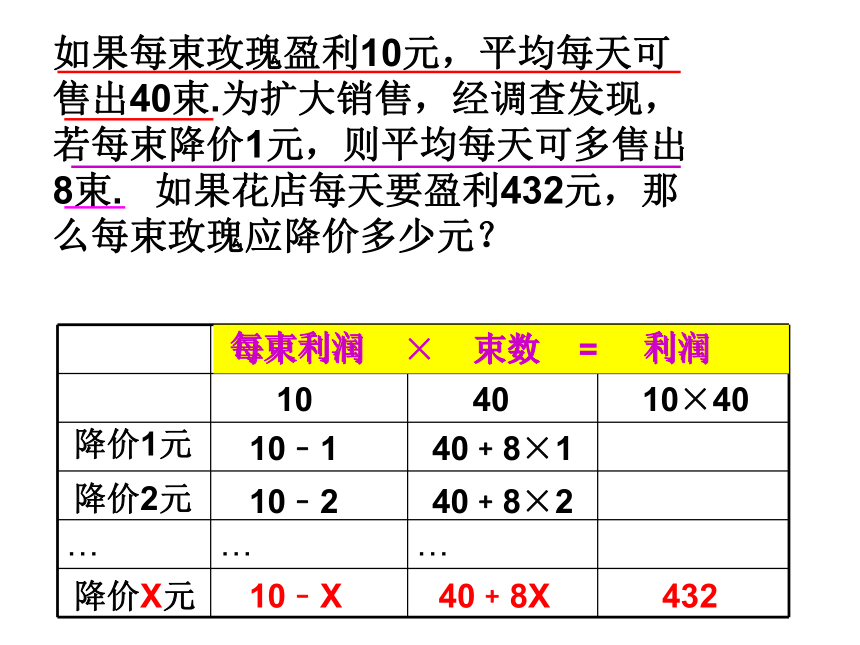
如果每束玫瑰盈利10元,平均每天可售出40束.为扩大销售,经调查发现,若每束降价1元,则平均每天可多售出8束. 如果花店每天要盈利432元,那么每束玫瑰应降价多少元?
… … …
每束利润 × 束数 = 利润
每束利润
束数
10
40
利润
10×40
降价1元
10﹣1
40﹢8×1
降价2元
10﹣2
40﹢8×2
降价X元
10﹣X
40﹢8X
432
解:设每束玫瑰应降价X元,则每束获利
(10-X)元,平均每天可售出(40+8X)束,
(10-X)(40+8X)= 432
化简整理得:
X2-5X+4=0
解得:
X1=1 X2=4
检验:X1=1 ,X2=4 都是方程的解
等量关系
( )×( )
每束利润
束数
利润
=
由题意得:
10-X
40+8X
432
能不能用因式分解法
小新家每天要盈利432元,
那么每束玫瑰应降价1元或4元。
答:
金陵路商业街某花店,如果每束玫瑰盈利10元,平均每天可售出40束.为扩大销售,经调查发现,若每束降价1元,则平均每天可多售出8束.如果花店每天要盈利432元,同时也让顾客获得最大的实惠.那么每束玫瑰应降价多少元
生活情境一
解:设每束玫瑰应降价X元,则每束获利(10-X)元,平均每天可售出(40+8X) 束,
(10-X)(40+8X)= 432
整理得:
X2-5X+4=0
解得:
X1=1 X2=4
X2=4 是方程的解且符合题意
答:每束玫瑰应降价4元。
等量关系
( )×( )
每束利润
束数
利润
=
由题意得:
10-X
40+8X
432
要注意哦!
经检验: X1=1 不符合题意应舍去
列一元二次方程解应用题的基本步骤:
审
答
设
列
解
验
解:设每束玫瑰应降价X元,
则每束获利(10-X)元,
平均每天可售出(40+8X) 束,
( )×( )
等量关系
每束利润
束数
10-X
40+8X
432
=
利润
(10-X)(40+8X)= 432
X2-5X+4=0
X1=1 X2=4
检验:X1=1 不符合题意应舍去
X2=4 是方程的解且符合题意
答:花店每天要盈利432元,
那么每束玫瑰应降价4元。
由题意,得
解得:
验
审
解:设每盆花苗增加的株数为x株,则每盆花苗有______ 株,平均单株盈利为__________元.
由题意,得
(x+3)(3-0.5x)=10
x1=1, x2=2
(x+3)
(3-0.5x)
x2-3x+2=0
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
(1)小明家用花盆培育玫瑰花苗,小明经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
练习一
(2)欧尚超市销售一种饮料,平均每周可售出100箱,每箱利润120元,为了扩大销售,增加利润,超市准备特价销售。据测算,若每箱降价10元,每周可多售出2箱。如果要使每天销售饮料获利14000元,问每箱应降价多少元?(仅需列出方程)
练习二
(1)春节过后,许多服装都降价处理,中百一店一件皮衣原售价2000元, 第一次下降10%,下降后售价________元,由于天气逐渐转暖,为了减少库存,第二次又下降了10%,此时售价__________ 元。(只需写出算式)
(2)某公司今年的销售收入是a万元,如果每年的平均增长率都是x,那么一年后的销售收入将达到____ _ 万元,两年后的销售收入将达到__ ____万元(用代数式表示)
a(1+x)
a(1+x)2
二次增长后的值为
依次类推n次增长后的值为
设基数为a,平均增长率为x,则一次增长后的值为
设基数为a,平均降低率为x,则一次降低后的值为
二次降低后的值为
依次类推n次降低后的值为
(1)增长率问题
(2)降低率问题
a(1+x)
a(1+x)2
a(1+x)n
a(1-x)
a(1-x)2
a(1-x)n
例2.截止到2000年12月31日,我国的上网计算机总数为892万台;截止到2002年12月31日,我国的上网计算机总数以达2083万台.
(1)求2000年12月31日至2002年12月31日我国的上网计算机台数的年平均增长率(精确到0.1%).
思考:(1)若设年平均增长率为x,你能用x的代数式表示2002年的台数吗
(2)已知2002年的台数是多少
(3)据此,你能列出方程吗
892(1+x)2=2083
.
.
.
.
.
年份
上网计算 机总台数
(万台)
3200
2400
1600
800
0
2000年
1月1日
2000年
12月31日
2001年
12月31日
2002年
12月31日
2003年
12月31日
350
892
1254
2083
3089
生活情境二
长兴冶炼厂2008年1月份铜产量为4万吨,产量平均每月的增长率相同.3月份铜产量为4.84万吨,则2,3月份平均每月的增长率是多少
某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年近视学生人数的75℅,设这两年平均每年近视学生人数降低的百分率为x,则可列方程为______________.
提示:增长率问题中若基数不明确,
通常可设为“1”,或设为a等等,
设为“1”更常用.
练一练:
(1)列一元二次方程解应用题的基本步骤:
审.设.列.解.验.答
(2)商品售价问题
(3) 增长率降低率问题
受全球金融危机影响,世纪联华超市将某种商品的售价从原来的每件40元经两次调价后调至32.4元.
(1)若该超市两次调价的降价率相同,求这个降价率.
(2)经调查,该商品每降价0.2元,即可多销售10件,若该商品原来每月可销售500件,那么两次调价后,每月可销售该商品多少件
金陵路商业街某花店,如果每束玫瑰盈利10元,平均每天可售出40束.为扩大销售,经调查发现,若每束降价1元,则平均每天可多售出8束.如果花店每天要盈利432元, 那么每束玫瑰应降价多少元
生活情境一
如果每束玫瑰盈利10元,平均每天可售出40束.为扩大销售,经调查发现,若每束降价1元,则平均每天可多售出8束. 如果花店每天要盈利432元,那么每束玫瑰应降价多少元?
… … …
每束利润 × 束数 = 利润
每束利润
束数
10
40
利润
10×40
降价1元
10﹣1
40﹢8×1
降价2元
10﹣2
40﹢8×2
降价X元
10﹣X
40﹢8X
432
解:设每束玫瑰应降价X元,则每束获利
(10-X)元,平均每天可售出(40+8X)束,
(10-X)(40+8X)= 432
化简整理得:
X2-5X+4=0
解得:
X1=1 X2=4
检验:X1=1 ,X2=4 都是方程的解
等量关系
( )×( )
每束利润
束数
利润
=
由题意得:
10-X
40+8X
432
能不能用因式分解法
小新家每天要盈利432元,
那么每束玫瑰应降价1元或4元。
答:
金陵路商业街某花店,如果每束玫瑰盈利10元,平均每天可售出40束.为扩大销售,经调查发现,若每束降价1元,则平均每天可多售出8束.如果花店每天要盈利432元,同时也让顾客获得最大的实惠.那么每束玫瑰应降价多少元
生活情境一
解:设每束玫瑰应降价X元,则每束获利(10-X)元,平均每天可售出(40+8X) 束,
(10-X)(40+8X)= 432
整理得:
X2-5X+4=0
解得:
X1=1 X2=4
X2=4 是方程的解且符合题意
答:每束玫瑰应降价4元。
等量关系
( )×( )
每束利润
束数
利润
=
由题意得:
10-X
40+8X
432
要注意哦!
经检验: X1=1 不符合题意应舍去
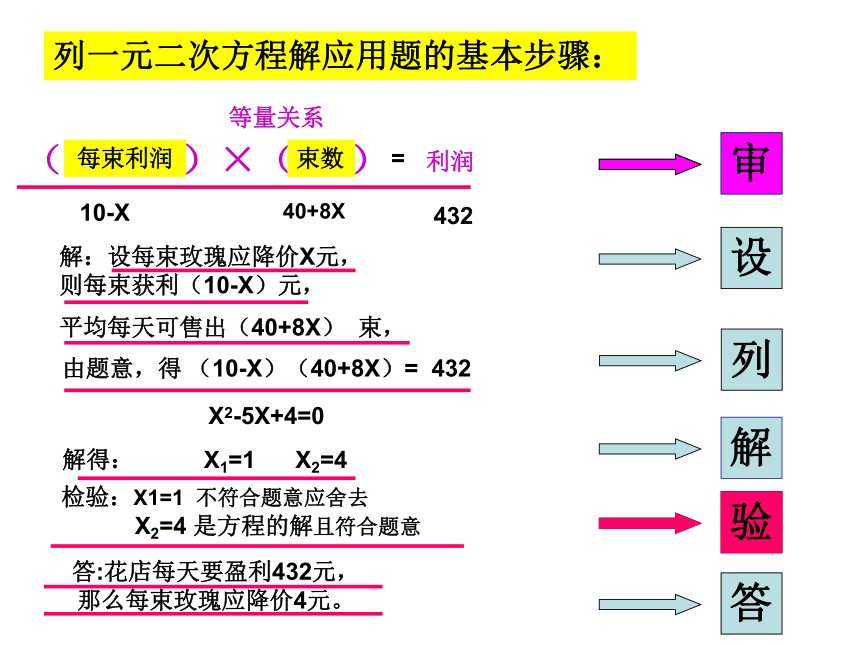
列一元二次方程解应用题的基本步骤:
审
答
设
列
解
验
解:设每束玫瑰应降价X元,
则每束获利(10-X)元,
平均每天可售出(40+8X) 束,
( )×( )
等量关系
每束利润
束数
10-X
40+8X
432
=
利润
(10-X)(40+8X)= 432
X2-5X+4=0
X1=1 X2=4
检验:X1=1 不符合题意应舍去
X2=4 是方程的解且符合题意
答:花店每天要盈利432元,
那么每束玫瑰应降价4元。
由题意,得
解得:
验
审
解:设每盆花苗增加的株数为x株,则每盆花苗有______ 株,平均单株盈利为__________元.
由题意,得
(x+3)(3-0.5x)=10
x1=1, x2=2
(x+3)
(3-0.5x)
x2-3x+2=0
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
(1)小明家用花盆培育玫瑰花苗,小明经过试验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
练习一
(2)欧尚超市销售一种饮料,平均每周可售出100箱,每箱利润120元,为了扩大销售,增加利润,超市准备特价销售。据测算,若每箱降价10元,每周可多售出2箱。如果要使每天销售饮料获利14000元,问每箱应降价多少元?(仅需列出方程)
练习二
(1)春节过后,许多服装都降价处理,中百一店一件皮衣原售价2000元, 第一次下降10%,下降后售价________元,由于天气逐渐转暖,为了减少库存,第二次又下降了10%,此时售价__________ 元。(只需写出算式)
(2)某公司今年的销售收入是a万元,如果每年的平均增长率都是x,那么一年后的销售收入将达到____ _ 万元,两年后的销售收入将达到__ ____万元(用代数式表示)
a(1+x)
a(1+x)2
二次增长后的值为
依次类推n次增长后的值为
设基数为a,平均增长率为x,则一次增长后的值为
设基数为a,平均降低率为x,则一次降低后的值为
二次降低后的值为
依次类推n次降低后的值为
(1)增长率问题
(2)降低率问题
a(1+x)
a(1+x)2
a(1+x)n
a(1-x)
a(1-x)2
a(1-x)n
例2.截止到2000年12月31日,我国的上网计算机总数为892万台;截止到2002年12月31日,我国的上网计算机总数以达2083万台.
(1)求2000年12月31日至2002年12月31日我国的上网计算机台数的年平均增长率(精确到0.1%).
思考:(1)若设年平均增长率为x,你能用x的代数式表示2002年的台数吗
(2)已知2002年的台数是多少
(3)据此,你能列出方程吗
892(1+x)2=2083
.
.
.
.
.
年份
上网计算 机总台数
(万台)
3200
2400
1600
800
0
2000年
1月1日
2000年
12月31日
2001年
12月31日
2002年
12月31日
2003年
12月31日
350
892
1254
2083
3089
生活情境二
长兴冶炼厂2008年1月份铜产量为4万吨,产量平均每月的增长率相同.3月份铜产量为4.84万吨,则2,3月份平均每月的增长率是多少
某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年近视学生人数的75℅,设这两年平均每年近视学生人数降低的百分率为x,则可列方程为______________.
提示:增长率问题中若基数不明确,
通常可设为“1”,或设为a等等,
设为“1”更常用.
练一练:
(1)列一元二次方程解应用题的基本步骤:
审.设.列.解.验.答
(2)商品售价问题
(3) 增长率降低率问题
受全球金融危机影响,世纪联华超市将某种商品的售价从原来的每件40元经两次调价后调至32.4元.
(1)若该超市两次调价的降价率相同,求这个降价率.
(2)经调查,该商品每降价0.2元,即可多销售10件,若该商品原来每月可销售500件,那么两次调价后,每月可销售该商品多少件
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
