5.4一元一次不等式组（1）

(共19张PPT)
5.4一元一次不等式组(1)
问题1:
不等式-X＞-2的解是( )
A. X＞2 B. X＞-2 C. X＜2 D. X＜-2
问题2:
C
不等式( )的解
在数轴表示,如图所示:
A. X＞-1 B. X＜-1 C. X≤-1 D. X≥-1
-2 -1 0 1 2
D
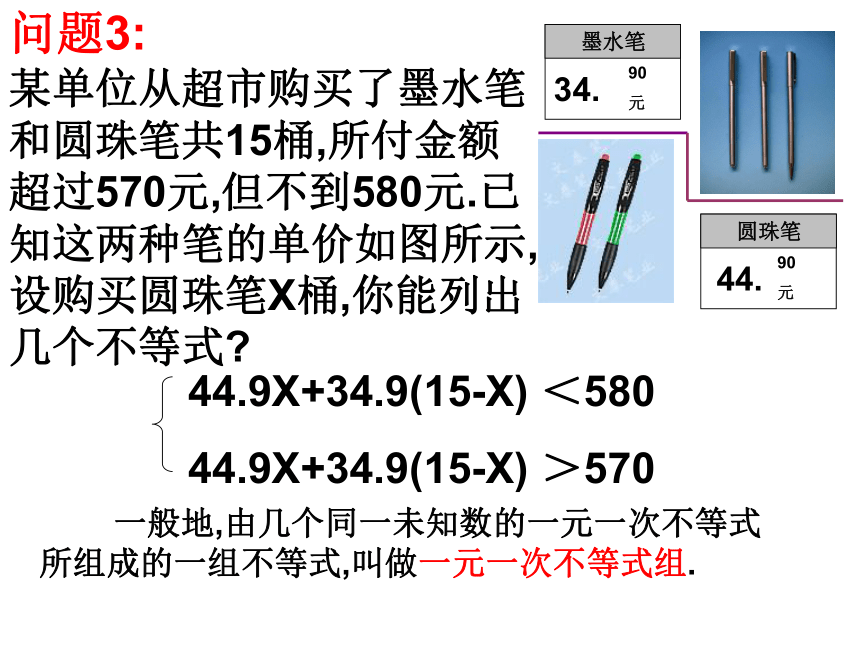
某单位从超市购买了墨水笔和圆珠笔共15桶,所付金额超过570元,但不到580元.已知这两种笔的单价如图所示,设购买圆珠笔X桶,你能列出几个不等式
问题3:
44.
90
元
圆珠笔
44.9X+34.9(15-X) ＜580
44.9X+34.9(15-X) ＞570
一般地,由几个同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.
34.
90
元
墨水笔
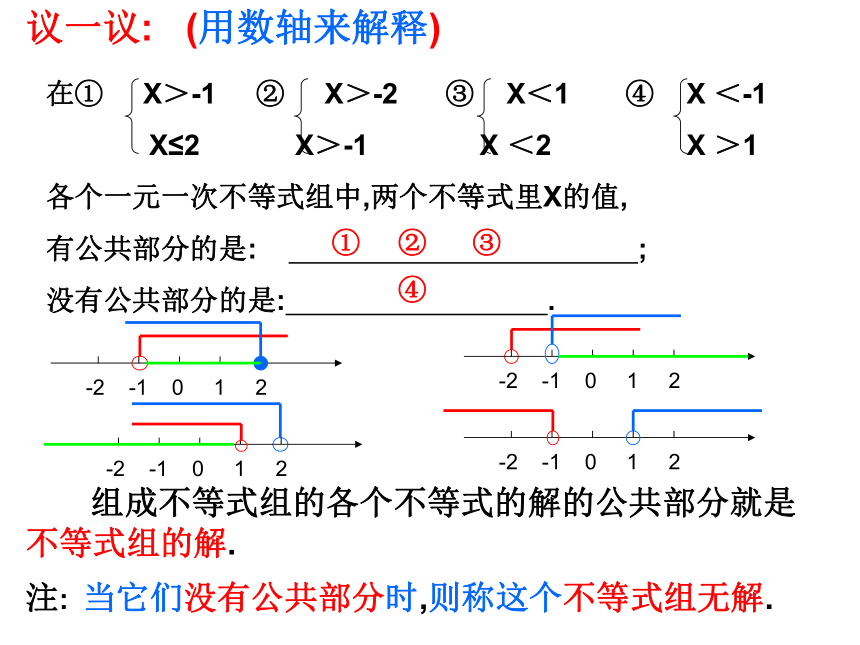
议一议: (用数轴来解释)
在① X＞-1 ② X＞-2 ③ X＜1 ④ X ＜-1
X≤2 X＞-1 X ＜2 X ＞1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是: ;
没有公共部分的是: .
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
②
④
组成不等式组的各个不等式的解的公共部分就是不等式组的解.
①
③
注: 当它们没有公共部分时,则称这个不等式组无解.
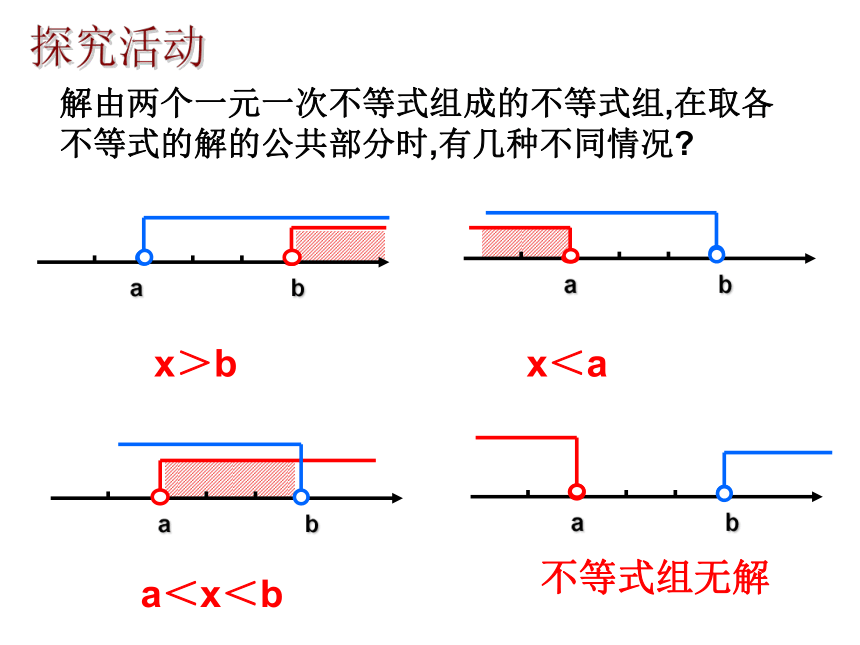
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
不等式组无解
a b
a b
x＞b
x＜a
a＜x＜b
解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
探索研究
若m＜n,你能说出下列四种情况下,不等式组的解吗 用数轴试一试.
x＞ m (2) x＞ m (3) x＜ m (4) x＜m
x＜n x ＞n x＜n x＞n
(请你与同伴交流)
m＜x＜n ; x＞n ; x＜m ; 无解
大小小大, 大大,取大 小小,取小 小小大大,
取两数之间 无解
注: 以上规律建立在最简不等式组的基础上
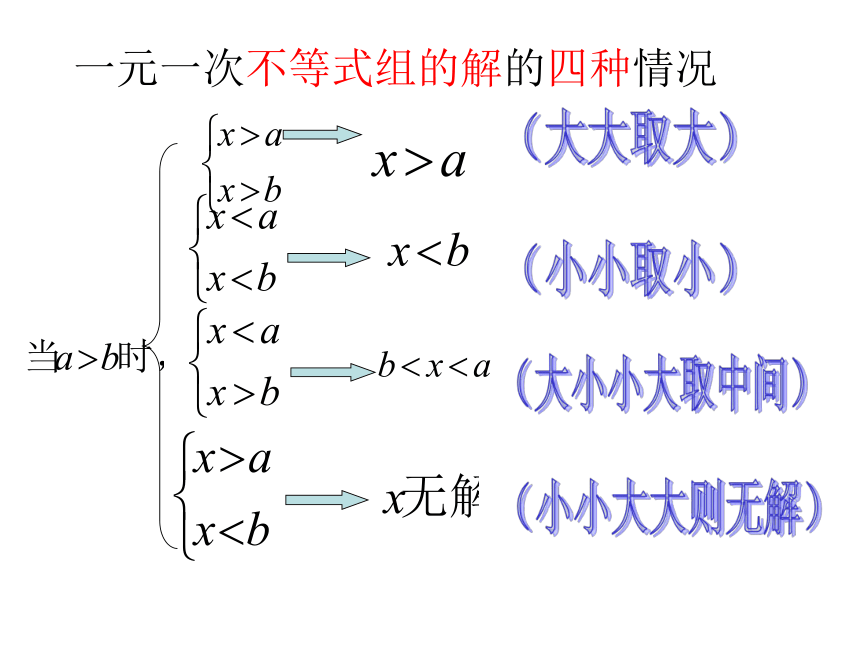
一元一次不等式组的解的四种情况
例1:解一元一次不等式组 3X+2＞X ①
X≤2 ②
解:
分析: 根据一元一次不等式组解的意义, 只要求出各不等式的解的公共部分即可.
解不等式①,得X＞-1
解不等式②,得X≤6
把①, ②两不等式的解表示在数轴上(如图)
-3 -2 -1 0 1 2 3 4 5 6
所以原不等式组的解是 -1＜X≤6
例2:解一元一次不等式组 3-5X＞X-2(2X-1) ①
②
此题与上题有何不同
解: 解不等式①,得 X＜
解不等式②,得 X＞
把① ,②两个不等式的解表示在数轴上
所以原不等式组无解
解一元一次不等式组的步骤:
(1)分别求出各不等式的解
(2)将它们的解表示在同一数轴上
(3)求原不等式组的解(即为它们解的公共部分).
-3 -2 -1 0 1 2 3 4 5 6
3x-2
4
>2.5-
x
2
练一练:
2.求出P108节前图中,圆珠笔和墨水笔的桶数.
X＞4.56 即整数X=5, 所以15-5=10
X＜5.56
课内练习P110第二题（1）（2）
1.解下列各一元一次不等式组
思考题:
1.解不等式组: 2-x＜x≤6-2x
2.若不等式组 x＞-a 的解为 x≥-b ,则下列各式正确的是( ) x≥-b
A. a＞b B. a＜b C. b ≤a D. ab＞0
A
解为 1＜x≤2
1. 不等式组
的整数解的个数是：( ) 　　A、1　　　B、2　　　C、3　　　D、0
2. 若不等式组
的解集为x>3，则m的取值范围是( ) 　　A、m≥3　　　B、m=3　　　C、m<3　　　D、m≤3
　　
C
D
解不等式组：　　　　　　　　
变式1：两个代数式x-1与x+3的值的符号相同，则x的取值范围是多少？
变式2：若　　　　　　　　，不等式
组　　　　　　　的解集是多少？　　
变式３：方程组　　　　　　　　的解是
　　　则不等式组　　　　的解是多少？
x+3>0 ①
x-1>0 ②
3、使方程组 的解 x 、 y都是正数，
a的取值范围。
解： (1) ×5 －(2)，得：x＝7＋a (3)
把(3)代入(1)，得：y＝－5 －2a
4、若关于x的不等式
无解，求m的取值范围 。
解：由（1）得: x<2
由（2）得：x>m － 1
X有解，错误
(2) m － 1=2
(3) m － 1>2
思考题：
已知关于x的不等式组 的整数解
共有4个，求a的取值范围。
解：由（1）得：x ≥a+1
由（2）得：x<2
有整数解4个
考虑五种情况
（1） a+1= － 1
数轴为
此时只有3个整数解
（不符合四个解，舍去）
(2) －2数轴为
此时只有3个整数解
（不符合四个解，舍去）
(3)a+1= －2
数轴为
此时只有4个整数解（符合）
(4) －3数轴为
此时只有4个整数解（符合）
(5)a+1=－3
数轴为
此时有5个整数解
（不符合四个解，舍去）
小结:
(1)一元一次不等式组的概念
(2)一元一次不等式组的解的概念
(3)解一元一次不等式组的步骤和解的四种情况.
作业: (1)作业本5.4(1)
(2)课本中作业题