相似三角形复习

(共20张PPT)
2009冬季风云变幻
试题来源
（浙教版九年级上册4.4-2作业本29页第3题）
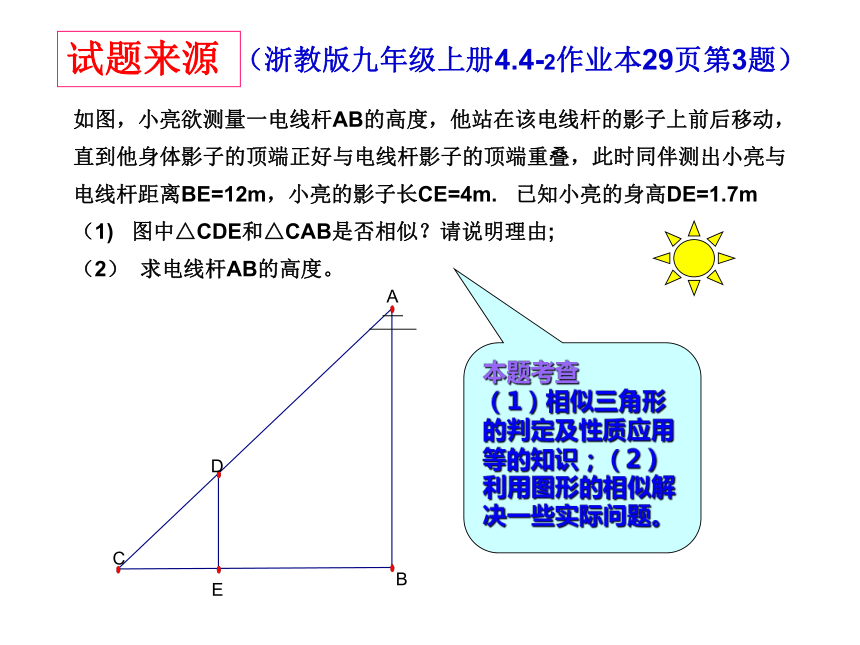
如图，小亮欲测量一电线杆AB的高度，他站在该电线杆的影子上前后移动，
直到他身体影子的顶端正好与电线杆影子的顶端重叠，此时同伴测出小亮与
电线杆距离BE=12m，小亮的影子长CE=4m. 已知小亮的身高DE=1.7m
（1) 图中△CDE和△CAB是否相似？请说明理由;
（2） 求电线杆AB的高度。
本题考查
（1）相似三角形的判定及性质应用等的知识；（2）利用图形的相似解决一些实际问题。
遮挡物为竖直的平面
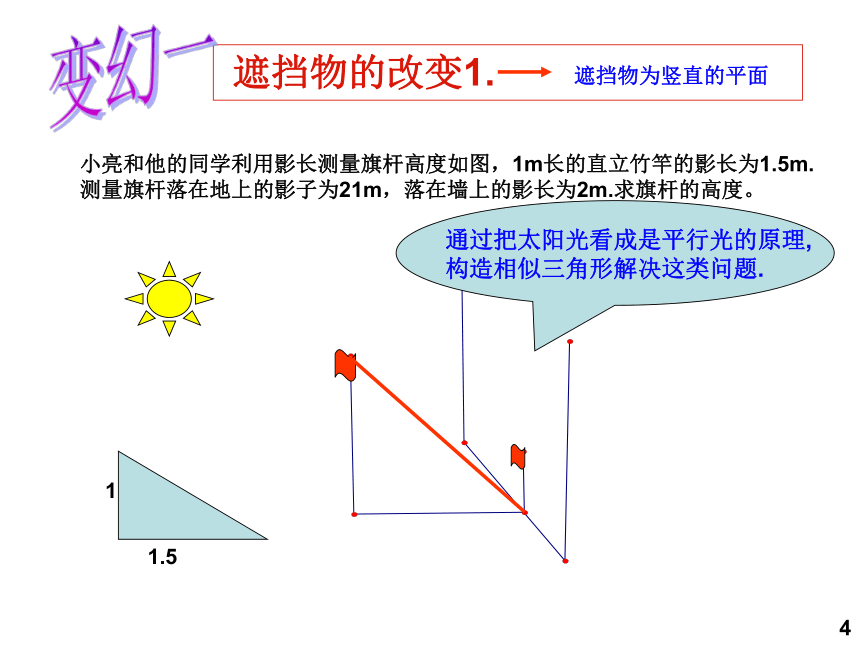
小亮和他的同学利用影长测量旗杆高度如图，1m长的直立竹竿的影长为1.5m.
测量旗杆落在地上的影子为21m，落在墙上的影长为2m.求旗杆的高度。
1
1.5
通过把太阳光看成是平行光的原理,
构造相似三角形解决这类问题.
4
遮挡物的改变1.
1
1.5
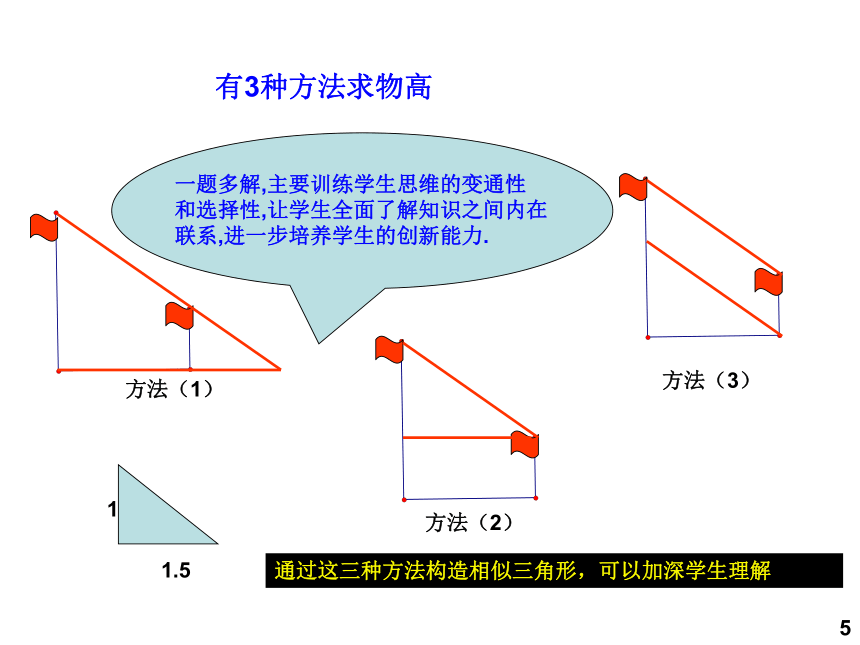
有3种方法求物高
通过这三种方法构造相似三角形，可以加深学生理解
一题多解,主要训练学生思维的变通性
和选择性,让学生全面了解知识之间内在
联系,进一步培养学生的创新能力.
5
方法（1）
方法（2）
方法（3）
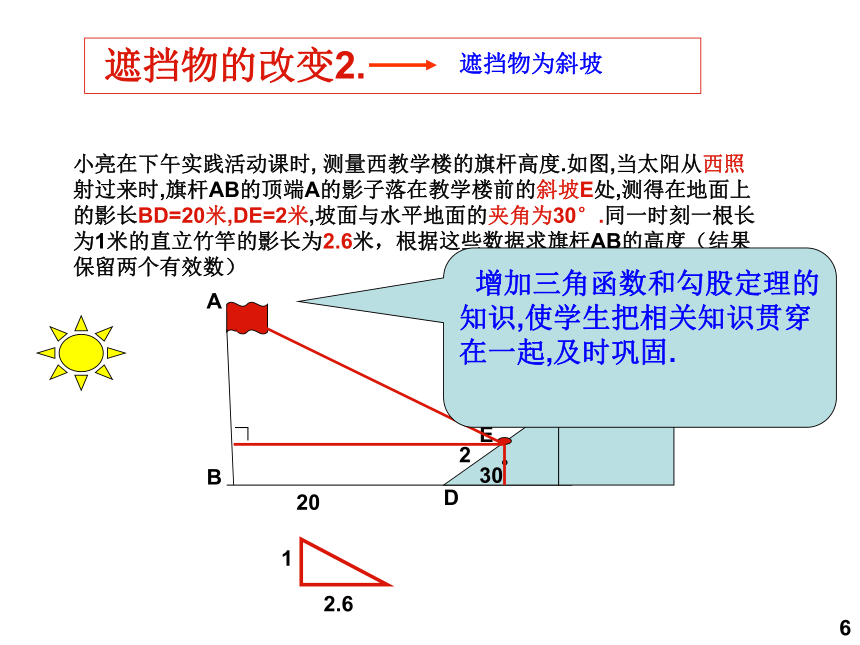
小亮在下午实践活动课时, 测量西教学楼的旗杆高度.如图,当太阳从西照
射过来时,旗杆AB的顶端A的影子落在教学楼前的斜坡E处,测得在地面上
的影长BD=20米,DE=2米,坡面与水平地面的夹角为30°.同一时刻一根长
为1米的直立竹竿的影长为2.6米，根据这些数据求旗杆AB的高度（结果
保留两个有效数）
°
30
A
B
D
E
20
2
∟
1
2.6
遮挡物为斜坡
6
增加三角函数和勾股定理的知识,使学生把相关知识贯穿在一起,及时巩固.
遮挡物的改变2.
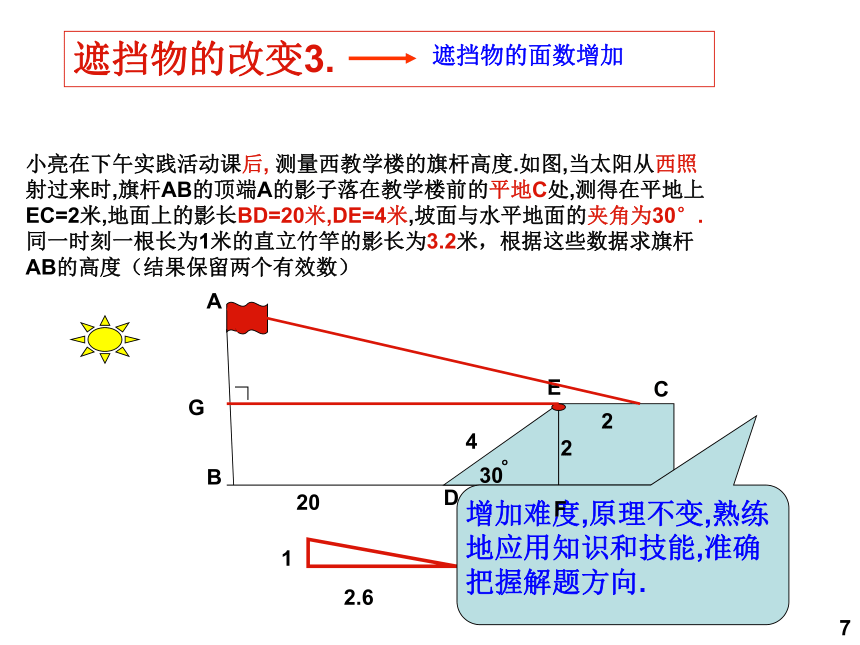
小亮在下午实践活动课后, 测量西教学楼的旗杆高度.如图,当太阳从西照
射过来时,旗杆AB的顶端A的影子落在教学楼前的平地C处,测得在平地上
EC=2米,地面上的影长BD=20米,DE=4米,坡面与水平地面的夹角为30°.
同一时刻一根长为1米的直立竹竿的影长为3.2米，根据这些数据求旗杆
AB的高度（结果保留两个有效数）
°
30
A
B
D
E
20
4
∟
1
2.6
C
2
遮挡物的面数增加
遮挡物的改变3.
7
增加难度,原理不变,熟练
地应用知识和技能,准确
把握解题方向.
F
2
G
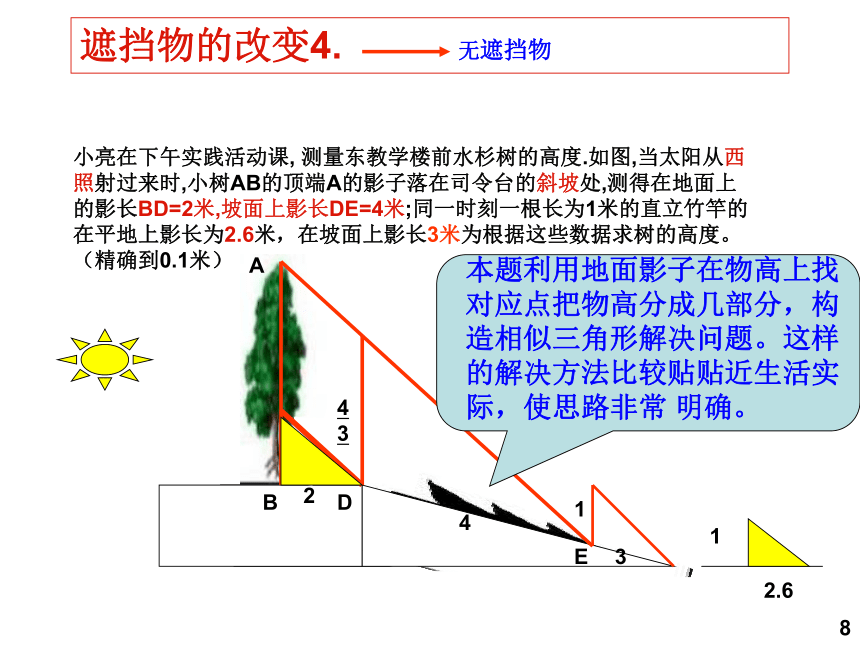
小亮在下午实践活动课, 测量东教学楼前水杉树的高度.如图,当太阳从西照射过来时,小树AB的顶端A的影子落在司令台的斜坡处,测得在地面上
的影长BD=2米,坡面上影长DE=4米;同一时刻一根长为1米的直立竹竿的在平地上影长为2.6米，在坡面上影长3米为根据这些数据求树的高度。（精确到0.1米）
遮挡物的改变4.
A
B
D
2.6
2
4
E
1
3
4
3
1
无遮挡物
8
本题利用地面影子在物高上找对应点把物高分成几部分，构造相似三角形解决问题。这样的解决方法比较贴贴近生活实际，使思路非常 明确。
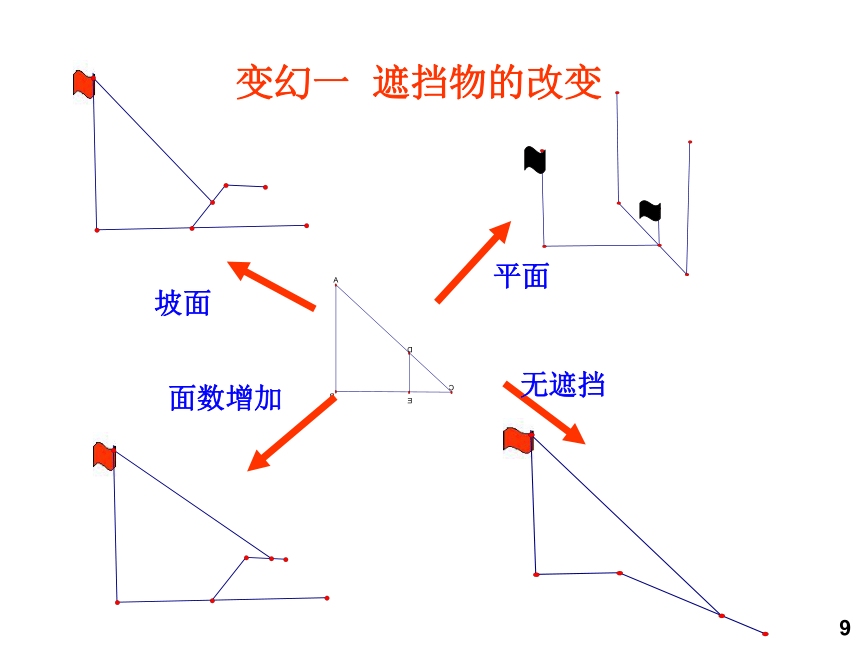
平面
坡面
面数增加
变幻一 遮挡物的改变
9
无遮挡
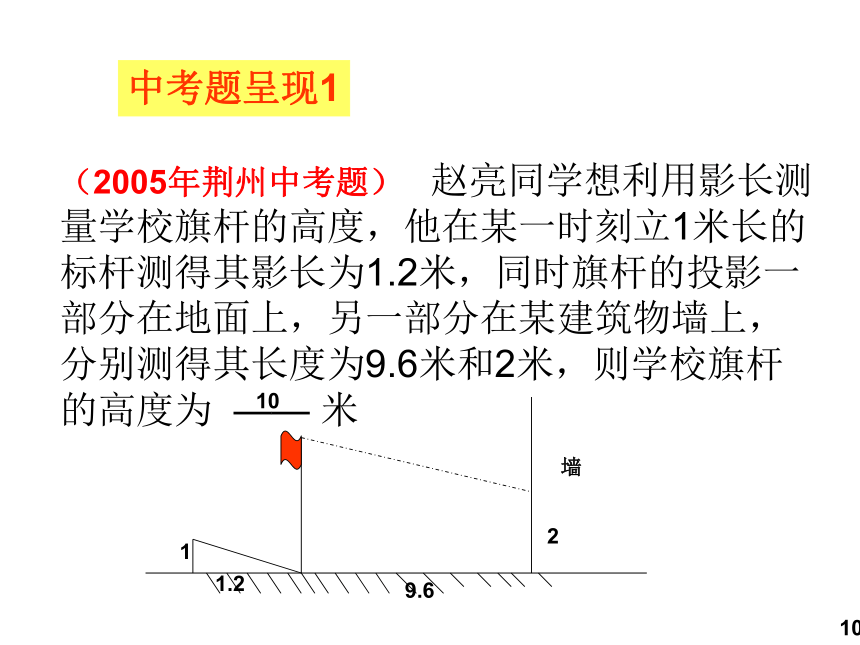
（2005年荆州中考题） 赵亮同学想利用影长测量学校旗杆的高度，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上，另一部分在某建筑物墙上，分别测得其长度为9.6米和2米，则学校旗杆的高度为 —— 米
中考题呈现1
10
1
1.2
9.6
2
墙
10
（第9题图）
（2008年中考题绍兴市9）．兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为（ C ）
A．11.5 B．11.75米 C．11.8米 D．12.25米
中考题的呈现2
11
（2007年宁波中考题12）．如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12 m，塔影长DE=18 m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为( ) (A)24m (B)22m (C)20 m (D)18 m
A
中考题的呈现3
12
晚上，小亮晚自修结束回寝室途中，走到C处时，发现在点B上方的路灯A照
得自己的影子CD的长为2米；继续往前走4米到达E处时，这时自己的影子EF
长为4米 ,已知小亮的身高为1.6米 ，
（1）路灯的高度等于多少？
A
B
F
E
C
D
参照物的移动(1)
根据相似三角形对应边
成比例，并利用等量代换
求解。
13
这类题目有变量和不变
的量，注意挖掘里面的
等量关系
4.8
（2）小亮探究影子长度的变化规律，当他走到离路灯2米处时，其影子
的顶点标记为H1，此时 影长为 米；当他继续走到H1时，其
影子的顶点标记为H2，此时影长为 米；当他继续走到H2时，
其影子的顶点标记为H3，此时影长为 米；…按这样的规律继
续走当他走到Hn,其影子的顶点标记为Hn+1,此时影长为 米。
1
A
B
H1
H2
H4
H3
参照物的移动（2）.
14
让题设条件进行变化，克服学
生思维定势。充分渗透数学猜
想和归纳法，培养学生探究能
力和发散思维能力。
4.8
2
1.6
A1
B2
E
H
A
B
C
中考题呈现
及时巩固
15
（2007年金华中考，23）学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图，在同一时间，身高为1.6m的小明(AB)的影子BC长是3m，而小颖EH刚好在路灯灯泡的正下方H点，并测得HB=6m．
（1）请在图中画出形成影子的光线，交确定路灯灯泡所在的位置G；
（2）求路灯灯泡的垂直高度GH；
（3）如果小明沿线段BH向小颖（点H）走去，当小明走到BH中点B1
处时，求其影子B1C1的长；当小明继续走剩下路程的 到B2处时,
求其影子B2C2的长；当小明继续走剩下路程的 到B3处，…按此规
律继续走下去，当小明走剩下路程的 到处时，其影子BnCn的长为 m（直接用的代数式表示）
(3/n+1)
（2006年金华中考）
如图,平面直角坐标系中,直线AB与轴,轴分别交于A(3,0),B(0, √3)两点, ,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
(1)求直线AB的解析式;
(2)若梯形OBCD的面积为 , 求点C的坐标;
(3)在第一象限内是否存在点P,使得以P,O,B为顶点的
三角形与△OBA相似.若存在,请求出所有符合条件
的点P的坐标;若不存在,请说明理由.
添加材料，与一次函数结合
p2
p1
p3
p4
∠OBP=90°两种情况
△BOP1∽ △ OBA
△BP2O∽ △ OBA
∠OPB=90°两种情况
△P3B O∽ △ OBA
△P4OB∽ △ OBA
4
√3
3
16
通过添加直角坐标系，与函数结合。充分运用数形结合思想，方程思想以及分类讨论的思想，考查梯形，相似三角形，图形与坐标，一次函数等知识。训练学生对知识的灵活运用，培养其综合分析问题的能力。
添加材料，与二次函数结合
如图，在平面直角坐标系内，AC⊥X轴于点C（1，0），BD ⊥X轴于
点D（4，0）直线AB与X,Y轴交于点E,F且解析式y=kx+4,四边形ABCD
的面积为7.
(1)求F.C.D三点的抛物线的解析式;
(2)求k 的值；
A
F
O
B
D
E
C
17
培养图形构造和观察
能力，使知识进一步渗
透到不同领域,培养学生
综合应用能力。
（2008年衢州中考）10如图，点O在Rt△ABC的斜边AB上，⊙O切AC边于点E，切BC边于点D， 连结OE，如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等，
那么BC 的值约为(∏取3.14) ( )
AC
A、2.7 B、2.5 C、2.3 D、2.1
A
O
E
C
D
B
添加材料，与圆结合
C
18
由扇形与正方形的面积公式
求得阴影面积，再得到OE
与AE得比值，即得最后答案
渗透
转化思想。
19
千变万化，形变意不变
基本图形
感悟
1.体会数学与生活密不可分，中考的问题背景一般都非常贴近生活。
2.学会挖掘图中条件，解决实际问题。
3.培养了学生思维的灵活性和发散性。
4.掌握数学思想和方法 .
20