1.4全等三角形

(共20张PPT)
仔细观察下列各组图形，你发现了什么？
两个图形的形状和大小完全相同。
能够重合的两个图形叫做全等图形
如果把这些形状和大小一样的图形叠合起来，会重合吗？
形状相同,但大小不同,
因此它们不是全等图形.
它们是全等图形吗？
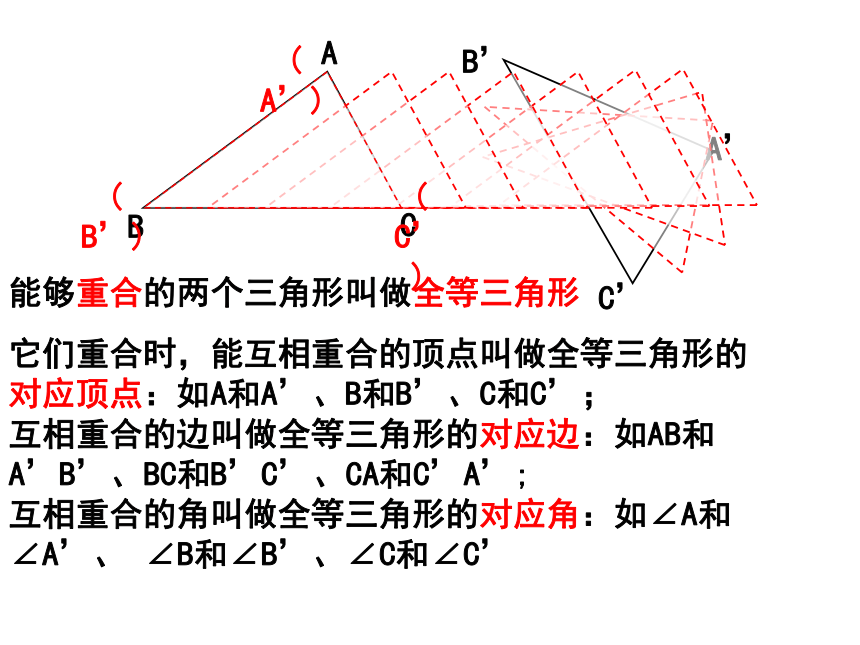
能够重合的两个三角形叫做全等三角形
A
B
C
A’
B’
C’
(A’)
(B’)
(C’)
它们重合时，能互相重合的顶点叫做全等三角形的对应顶点：如A和A’、B和B’、C和C’； 互相重合的边叫做全等三角形的对应边：如AB和A’B’、BC和B’C’、CA和C’A’; 互相重合的角叫做全等三角形的对应角：如∠A和∠A’、 ∠B和∠B’、∠C和∠C’
A
B
C
A’
B’
C’
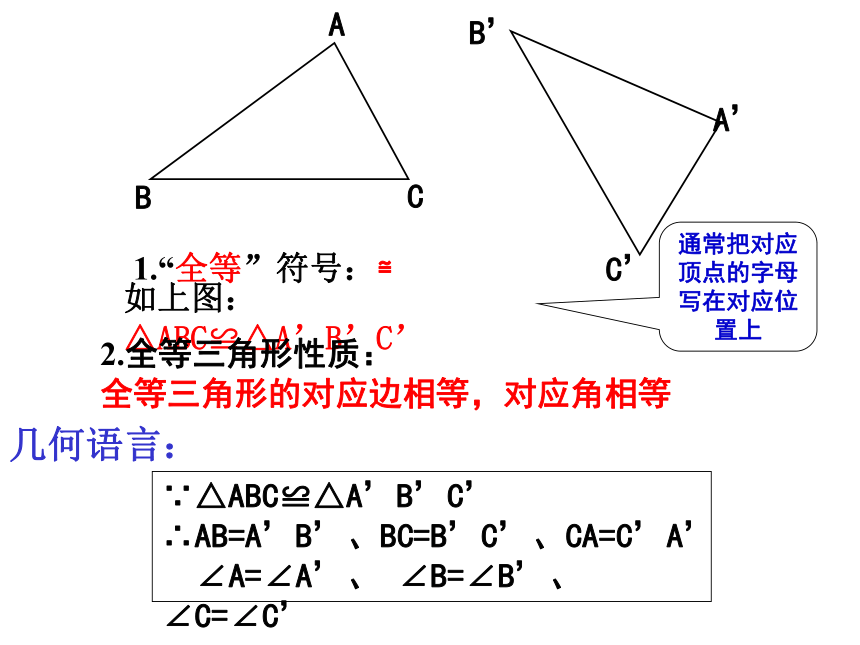
1.“全等”符号：≌
如上图：△ABC≌△A’B’C’
2.全等三角形性质： 全等三角形的对应边相等，对应角相等
∵△ABC≌△A’B’C’ ∴AB=A’B’、BC=B’C’、CA=C’A’ ∠A=∠A’、 ∠B=∠B’、 ∠C=∠C’
通常把对应顶点的字母写在对应位置上
几何语言：
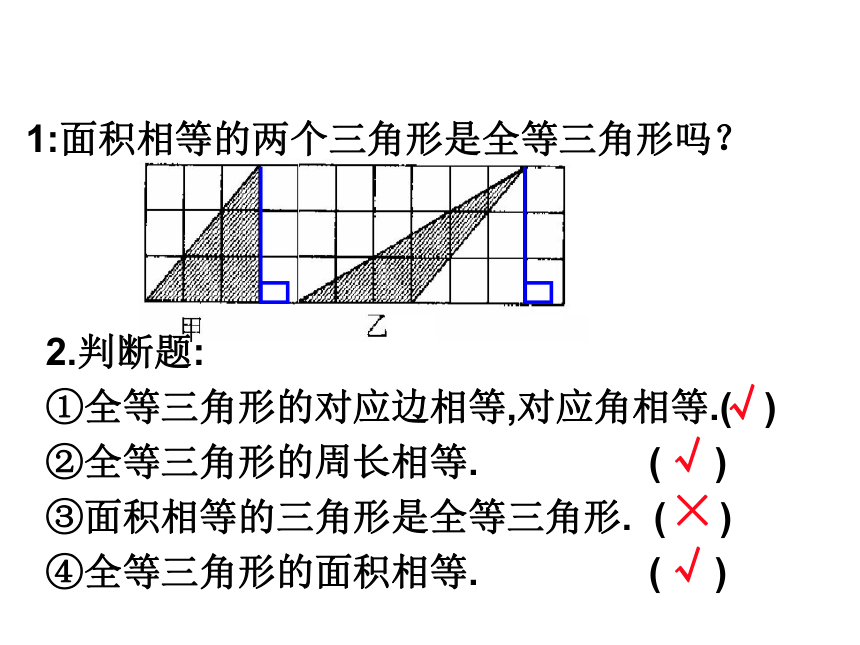
1:面积相等的两个三角形是全等三角形吗？
2.判断题:
①全等三角形的对应边相等,对应角相等.( )
②全等三角形的周长相等. ( )
③面积相等的三角形是全等三角形. ( )
④全等三角形的面积相等. ( )
√
√
√
×
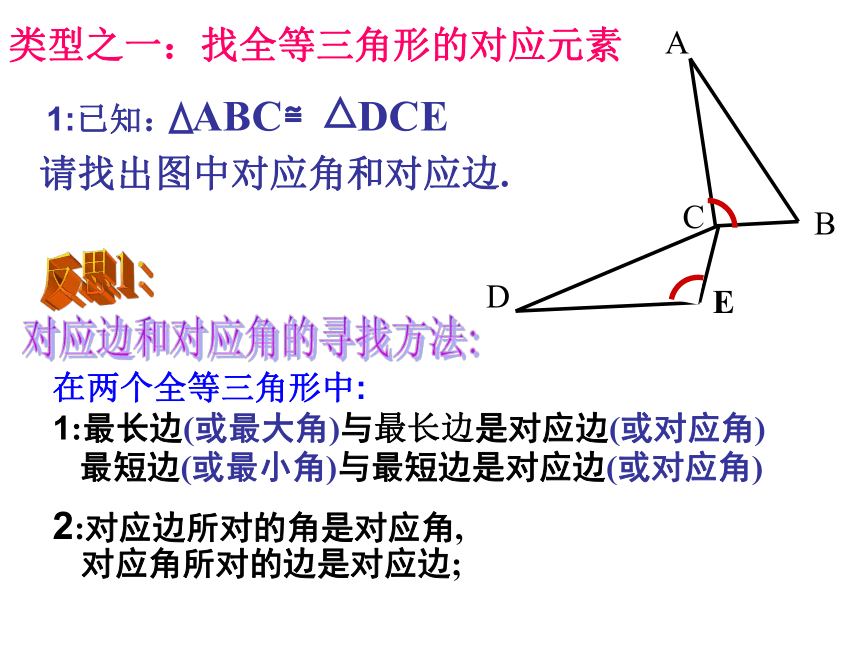
1:已知： ABC≌ DCE
请找出图中对应角和对应边.
A
B
C
D
E
在两个全等三角形中:
1:最长边(或最大角)与最长边是对应边(或对应角)
2:对应边所对的角是对应角,
最短边(或最小角)与最短边是对应边(或对应角)
对应角所对的边是对应边;
类型之一：找全等三角形的对应元素
A
B
C
D
请找出右图中对应的边和对应角.
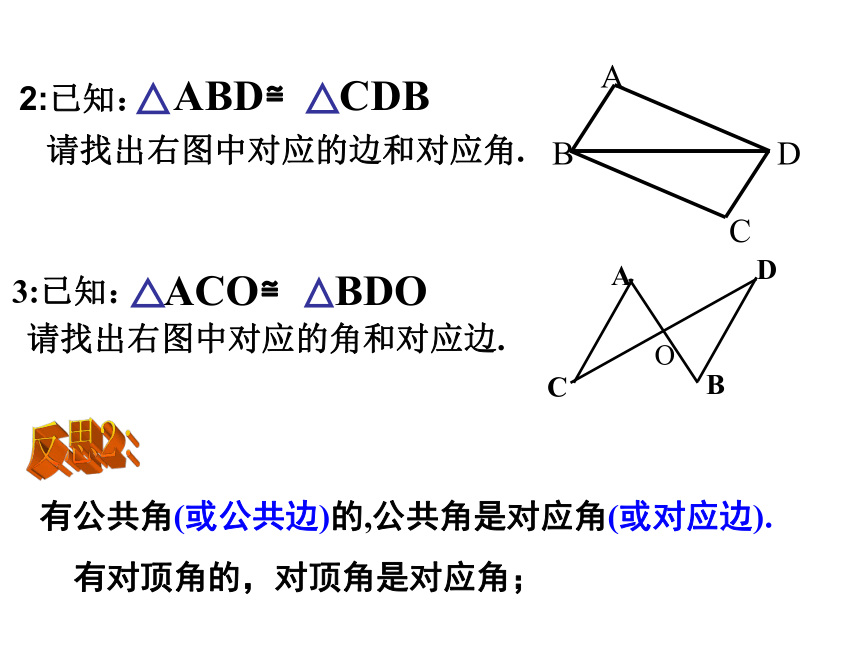
2:已知： ABD≌ CDB
ACO≌ BDO
3:已知：
请找出右图中对应的角和对应边.
有公共角(或公共边)的,公共角是对应角(或对应边).
A
B
O
C
D
有对顶角的，对顶角是对应角；
6:若△ABC≌△ADE,请找出对应边和对应角；
4:若△ABD≌△ACD,请找出对应边和对应角；
A
B
C
D
A
B
C
D
E
5:若△ABC≌△AED,请找出对应边和对应角；
D
A
E
C
B
7.已知图中的两个三角形全等，请你找出它们的对应角和对应边，并用符号表示这两个三角形全等。
8. 如图已知△ABC≌△ADE,∠C=∠E，BC=DE，其它的对应边有:_____,对应角有:_____.
A
B
C
D
E
例1:如图，点c是AB中点,△ACD≌△BCE，且
AD≠CE,
(1)写出△ACD与△BCE中相等的边与相等的角
(2) ∠ACE与∠BCD相等吗 说明理由.
A
D
E
C
B
类型之二：运用全等三角形的性质解决问题
变式：如图△ACF≌△DBE，且∠E=∠F
AD=9,BC=5,求AB的长.
A
B
C
E
F
D
1、如图，已知△ABD≌△ACE， 且∠1=45°,∠ADB=95°,则 ∠AEC= ∠C= .
1
A
E
B
C
D
2、如图，已知△ABC≌△DFE， 且AC与DE是对应边，若BE=14， FC=4，则BC= .
A
B
C
F
E
D
50°
95°
9
已知△ABD≌△ACE，且AB=8,DB=7,AD=6则BE=
巩固练习：
4:如图,点B,F,C,E在同一直线上,且△ABC≌ △DEF,若BF=1cm,BC=4cm,求线段BE的长.
D
F
E
A
C
B
5:如图, 已知△ABC≌ △ADE, ∠CAD=15°， ∠DFB=90°, ∠B=25°，求∠E和∠DGB的度数.
A
B
C
E
G
F
D
6:若△ABC≌△DEF，AC和DF，AB与DE是对应边，∠A=40°，∠B=30°BC=5cm,那么∠DFE=_____.EF=_________.
110°
　5cm
A
B
C
F
E
D
7: 如图△ ABD ≌ △CDB，若AB=4,DA=5，BD=6，则BC= ，CD= 。
A
B
C
D
5
4
( )
解：
∵
AD平分ABC
∴
∠1=∠2 因此将图形(图1)沿AD对折时，射线AC与射线_______重合
AB=AC
∵
点C与__重合，即△ABD与______重合(图2)
∴
△ABD≌△ACD
∴
BD=CD
∴
( )
∠B=∠C
( )
( )
( )
1
2
A
B
C
D
B(C)
A
D
图2
例2. 图1,AD平分∠ABC，AB=AC， (1)△ABD与△ACD全等吗？ (2)BD与CD相等吗 ∠B与∠C呢？请说明理由
全等三角形的对应角相等
已知
已知
AB
B
全等三角形的定义
全等三角形的对应边相等
△ACD
类型之三：运用全等三角形定义说明三角形全等
寻找对应元素的规律
（1）有公共边的，公共边是对应边；
（2）有公共角的，公共角是对应角；
（3）有对顶角的，对顶角是对应角；
（4）两个全等三角形最大的边是对应边，最小的边是对应边；
（5）两个全等三角形最大的角是对应角，最小的角是对应角；
（6）两个三角形全等时，对应顶点所在的角是对应角，对应边所对的角是对应角，对应角所对的边是对应边。　
归纳总结：
如图，BD是长方形ABCD的一条对角线。
（1）△ABD与△CDB全等吗？你是怎么知道的？
（2）如果你认为△ABD与△CDB全等，请用符号表示，并说出它们的对应边和对应角。
A
D
C
B
说一说：