2021年浙教版八年级下册课时训练:4.2 平行四边形及其性质 word含答案
文档属性
| 名称 | 2021年浙教版八年级下册课时训练:4.2 平行四边形及其性质 word含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览




文档简介
2021年浙教版八年级下册课时训练:4.2 平行四边形及其性质
一.选择题
1.平行四边形的两条对角线一定( )
A.互相平分 B.互相垂直 C.相等 D.以上都不对
2.在?ABCD中,∠A+∠C=200°,则∠A的度数为( )
A.130° B.100° C.80° D.70°
3.?ABCD中,∠A:∠B:∠C:∠D的度数比可能是( )
A.1:1:2:3 B.1:2:1:2 C.1:1:2:2 D.1:2:2:1
4.如图,平行四边形ABCD的周长为80,△BOC的周长比△AOB的周长多20,则BC长为( )
A.40 B.10 C.20 D.30
5.如图,?ABCD的周长为36cm,△ABC的周长为28cm,则对角线AC的长为( )
A.28cm B.18cm C.10cm D.8cm
6.如图,在?ABCD中,CE平分∠BCD交AD于点E,若AE=2,?ABCD的周长等于24,则线段AB的长为( )
A.5 B.6 C.7 D.8
7.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=6,BC=10,则EF长为( )
A.1 B.2 C.3 D.4
二.填空题
8.已知?ABCD中,∠B=4∠A,则∠A= .
9.如图,在?ABCD中,∠B=110°,则∠D= °.
10.如图,?ABCD的对角线AC、BD相交于点O,点E是AB的中点,△ABC的面积是16,则△BEO的面积为 .
11.如图,在平行四边形ABCD中,DE平分∠ADC,AD=5,BE=2,则平行四边形ABCD的周长是 .
12.如图,AC是?ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是 .
13.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是 .
14.如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=5,则平行四边形ABCD的周长为 .
三.解答题
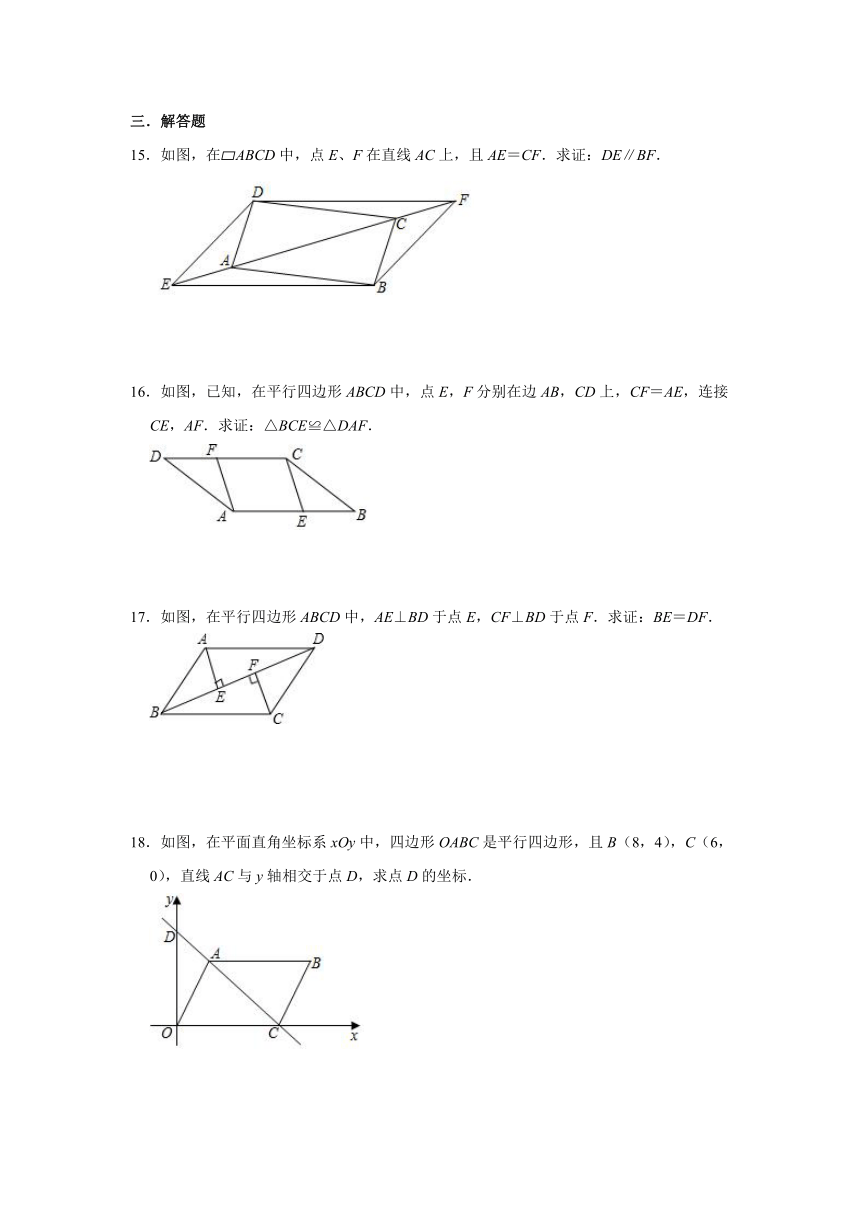
15.如图,在?ABCD中,点E、F在直线AC上,且AE=CF.求证:DE∥BF.
16.如图,已知,在平行四边形ABCD中,点E,F分别在边AB,CD上,CF=AE,连接CE,AF.求证:△BCE≌△DAF.
17.如图,在平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F.求证:BE=DF.
18.如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且B(8,4),C(6,0),直线AC与y轴相交于点D,求点D的坐标.
19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点A作AE⊥BD,垂足为点E,过点C作CF⊥BD,垂足为点F.
(1)求证:AE=CF;
(2)若∠AOE=74°,∠EAD=3∠CAE,直接写出∠BCA的度数.
20.如图,在?ABCD中,点O是对角线AC,BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S?ABCD=63,OE=3.5,求AD的长.
参考答案
一.选择题
1.解:因为平行四边形的两条对角线一定互相平分,菱形的对角线互相垂直,矩形的对角线相等,
所以A选项正确.
选:A.
2.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
又∵∠A+∠C=200°,
∴∠A=100°.
选:B.
3.解:根据平行四边形的两组对角分别相等,可知B正确.
选:B.
4.解:∵△BOC的周长比△AOB的周长多20,
∴BC﹣AB=20,①
∵平行四边形ABCD的周长为80,
∴BC+AB=40,②
由①+②,可得2BC=60,
∴BC=30.
选:D.
5.解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
选:C.
6.解:在?ABCD中,CE平分∠BCD交AD于点E,
∴∠DEC=∠ECB,∠DCE=∠BCE,AB=DC,AD=BC,
∴∠DEC=∠DCE,
∴DE=DC=AB,
∵ABCD的周长等于24,AE=2,
∴AB+AD=12,
∴AB+AE+DE=12,
∴AB=5.
选:A.
7.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=10,DC=AB=6.
∴∠AFB=∠FBC.
∵BF平分∠ABC,
∴∠ABF=∠FBC.
∴∠AFB=∠ABF.
∴AF=AB=6.
同理可得DE=DC=6.
∴EF=AF+DE﹣AD=6+6﹣10=2.
选:B.
二.填空题
8.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,
∴∠A+∠B=180°,
∵∠B=4∠A,
∴∠A=×180°=36°.
答案为:36°.
9.解:∵四边形ABCD是平行四边形,
∴∠B=∠D=110°.
答案为:110.
10.解:∵?ABCD的对角线AC、BD相交于点O,
∴OA=OC,
∵点E是AB的中点,
∴OE=BC,OE∥BC,
∴△AOE∽△ACB,
∴=,
∵△ABC的面积是16,
∴S△AOE=4,
∴S△BEO=4.
答案为:4.
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DEC=∠CDE,
∴CD=CE=BC﹣BE=AD﹣BE=5﹣2=3,
∴平行四边形ABCD的周长是2AD+2DC=10+6=16.
答案为:16.
12.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=102°,AD=BC,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,
∴∠CAB+∠ACB=3∠CAB=180°﹣∠ABC=180°﹣102°,
∴∠BAC=26°,
答案为:26°.
13.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
四边形AEMG和四边形HCFM的面积相等,即S1=S2.
答案为:S1=S2.
14.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠DAE+∠AEC=180°,
∵∠AEC=90°,∠EAF=45°,
∴∠EAD=90°,∠AGE=45°,
∴∠FAD=45°,
∵AF⊥CD,
∴∠AFD=90°,
∴∠D=45°,
∴△ABE和△AFD都是等腰直角三角形,
∵AE+AF=5,
∴设AE=x,则AF=5﹣x,
∴AB=x,AD=(5﹣x),
∴平行四边形ABCD的周长为:[x+(5﹣x)]×2=10,
答案为:10.
三.解答题
15.证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAF=∠BCE,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴∠DEA=∠BFC,
∴DE∥BF.
16.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∴∠D=∠B,
∵CF=AE,
∴BE=DF,
在△AFD与△CEB中,
∴△BCE≌△DAF(SAS).
17.证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABE=∠CDF,
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中
,
∴△ABE≌△CDF(AAS),
∴BE=DF.
18.解:∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,
∵B(8,4),C(6,0),
∴A(2,4),
设直线AC的解析式为y=kx+b,
∴,
解得:,
∴直线AC的解析式为y=﹣x+6,
当x=0时,y=6
∴点D的坐标为(0,6).
19.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
(2)解:∵AE⊥BD,
∴∠AEO=90°,
∵∠AOE=74°,
∴∠EAO=90°﹣∠AOE=16°,
∵∠EAD=3∠CAE,
∴∠EAD=3×16°=48°,
∴∠DAC=∠DAE﹣∠EAO=48°﹣16°=32°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BCA=∠DAC=32°.
20.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO,(ASA)
∴OE=OF;
(2)∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S?ABCD=AD×EF=63,
∴AD=9.
一.选择题
1.平行四边形的两条对角线一定( )
A.互相平分 B.互相垂直 C.相等 D.以上都不对
2.在?ABCD中,∠A+∠C=200°,则∠A的度数为( )
A.130° B.100° C.80° D.70°
3.?ABCD中,∠A:∠B:∠C:∠D的度数比可能是( )
A.1:1:2:3 B.1:2:1:2 C.1:1:2:2 D.1:2:2:1
4.如图,平行四边形ABCD的周长为80,△BOC的周长比△AOB的周长多20,则BC长为( )
A.40 B.10 C.20 D.30
5.如图,?ABCD的周长为36cm,△ABC的周长为28cm,则对角线AC的长为( )
A.28cm B.18cm C.10cm D.8cm
6.如图,在?ABCD中,CE平分∠BCD交AD于点E,若AE=2,?ABCD的周长等于24,则线段AB的长为( )
A.5 B.6 C.7 D.8
7.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=6,BC=10,则EF长为( )
A.1 B.2 C.3 D.4
二.填空题
8.已知?ABCD中,∠B=4∠A,则∠A= .
9.如图,在?ABCD中,∠B=110°,则∠D= °.
10.如图,?ABCD的对角线AC、BD相交于点O,点E是AB的中点,△ABC的面积是16,则△BEO的面积为 .
11.如图,在平行四边形ABCD中,DE平分∠ADC,AD=5,BE=2,则平行四边形ABCD的周长是 .
12.如图,AC是?ABCD的对角线,点E在AC上,AD=AE=BE,∠D=102°,则∠BAC的度数是 .
13.如图,过平行四边形ABCD的对角找BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与平行四边形HCFM的面积S2的大小关系是 .
14.如图,在?ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=5,则平行四边形ABCD的周长为 .
三.解答题
15.如图,在?ABCD中,点E、F在直线AC上,且AE=CF.求证:DE∥BF.
16.如图,已知,在平行四边形ABCD中,点E,F分别在边AB,CD上,CF=AE,连接CE,AF.求证:△BCE≌△DAF.
17.如图,在平行四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F.求证:BE=DF.
18.如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且B(8,4),C(6,0),直线AC与y轴相交于点D,求点D的坐标.
19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点A作AE⊥BD,垂足为点E,过点C作CF⊥BD,垂足为点F.
(1)求证:AE=CF;
(2)若∠AOE=74°,∠EAD=3∠CAE,直接写出∠BCA的度数.
20.如图,在?ABCD中,点O是对角线AC,BD的交点,EF过点O且垂直于AD.
(1)求证:OE=OF;
(2)若S?ABCD=63,OE=3.5,求AD的长.
参考答案
一.选择题
1.解:因为平行四边形的两条对角线一定互相平分,菱形的对角线互相垂直,矩形的对角线相等,
所以A选项正确.
选:A.
2.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
又∵∠A+∠C=200°,
∴∠A=100°.
选:B.
3.解:根据平行四边形的两组对角分别相等,可知B正确.
选:B.
4.解:∵△BOC的周长比△AOB的周长多20,
∴BC﹣AB=20,①
∵平行四边形ABCD的周长为80,
∴BC+AB=40,②
由①+②,可得2BC=60,
∴BC=30.
选:D.
5.解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
选:C.
6.解:在?ABCD中,CE平分∠BCD交AD于点E,
∴∠DEC=∠ECB,∠DCE=∠BCE,AB=DC,AD=BC,
∴∠DEC=∠DCE,
∴DE=DC=AB,
∵ABCD的周长等于24,AE=2,
∴AB+AD=12,
∴AB+AE+DE=12,
∴AB=5.
选:A.
7.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=10,DC=AB=6.
∴∠AFB=∠FBC.
∵BF平分∠ABC,
∴∠ABF=∠FBC.
∴∠AFB=∠ABF.
∴AF=AB=6.
同理可得DE=DC=6.
∴EF=AF+DE﹣AD=6+6﹣10=2.
选:B.
二.填空题
8.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠C,
∴∠A+∠B=180°,
∵∠B=4∠A,
∴∠A=×180°=36°.
答案为:36°.
9.解:∵四边形ABCD是平行四边形,
∴∠B=∠D=110°.
答案为:110.
10.解:∵?ABCD的对角线AC、BD相交于点O,
∴OA=OC,
∵点E是AB的中点,
∴OE=BC,OE∥BC,
∴△AOE∽△ACB,
∴=,
∵△ABC的面积是16,
∴S△AOE=4,
∴S△BEO=4.
答案为:4.
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DEC=∠CDE,
∴CD=CE=BC﹣BE=AD﹣BE=5﹣2=3,
∴平行四边形ABCD的周长是2AD+2DC=10+6=16.
答案为:16.
12.解:∵四边形ABCD是平行四边形,
∴∠ABC=∠D=102°,AD=BC,
∵AD=AE=BE,
∴BC=AE=BE,
∴∠EAB=∠EBA,∠BEC=∠ECB,
∵∠BEC=∠EAB+∠EBA=2∠EAB,
∴∠ACB=2∠CAB,
∴∠CAB+∠ACB=3∠CAB=180°﹣∠ABC=180°﹣102°,
∴∠BAC=26°,
答案为:26°.
13.解:∵四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
,
∴△ABD≌△CDB(SSS),
即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
四边形AEMG和四边形HCFM的面积相等,即S1=S2.
答案为:S1=S2.
14.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠DAE+∠AEC=180°,
∵∠AEC=90°,∠EAF=45°,
∴∠EAD=90°,∠AGE=45°,
∴∠FAD=45°,
∵AF⊥CD,
∴∠AFD=90°,
∴∠D=45°,
∴△ABE和△AFD都是等腰直角三角形,
∵AE+AF=5,
∴设AE=x,则AF=5﹣x,
∴AB=x,AD=(5﹣x),
∴平行四边形ABCD的周长为:[x+(5﹣x)]×2=10,
答案为:10.
三.解答题
15.证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAF=∠BCE,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS),
∴∠DEA=∠BFC,
∴DE∥BF.
16.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,
∴∠D=∠B,
∵CF=AE,
∴BE=DF,
在△AFD与△CEB中,
∴△BCE≌△DAF(SAS).
17.证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABE=∠CDF,
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中
,
∴△ABE≌△CDF(AAS),
∴BE=DF.
18.解:∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,
∵B(8,4),C(6,0),
∴A(2,4),
设直线AC的解析式为y=kx+b,
∴,
解得:,
∴直线AC的解析式为y=﹣x+6,
当x=0时,y=6
∴点D的坐标为(0,6).
19.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
(2)解:∵AE⊥BD,
∴∠AEO=90°,
∵∠AOE=74°,
∴∠EAO=90°﹣∠AOE=16°,
∵∠EAD=3∠CAE,
∴∠EAD=3×16°=48°,
∴∠DAC=∠DAE﹣∠EAO=48°﹣16°=32°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠BCA=∠DAC=32°.
20.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO,(ASA)
∴OE=OF;
(2)∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S?ABCD=AD×EF=63,
∴AD=9.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
