直线与圆圆与圆的位置关系复习

(共39张PPT)
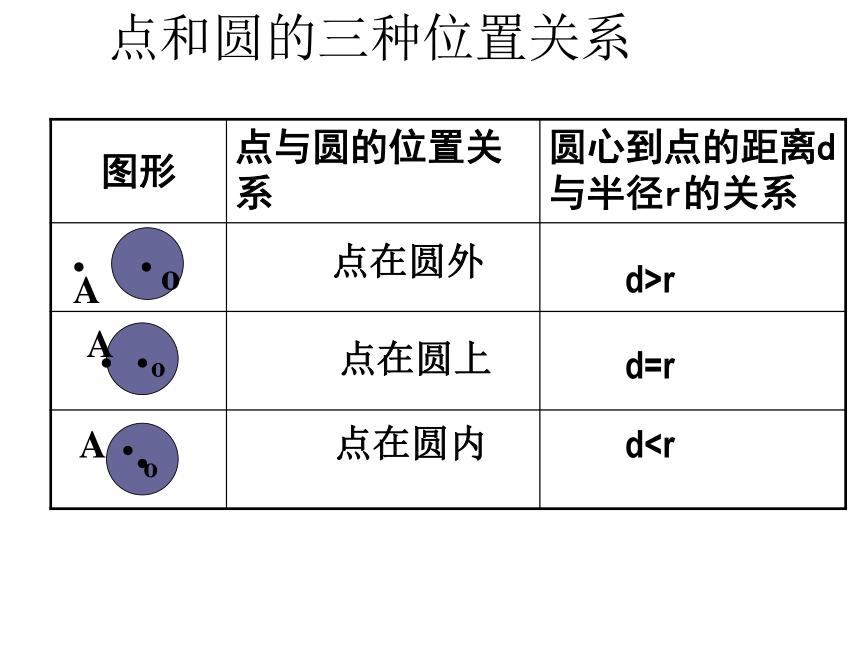
点和圆的三种位置关系
图形 点与圆的位置关系 圆心到点的距离d与半径r的关系
A
A
A






o
o
o
点在圆外
点在圆上
点在圆内
d>r
d=r
d直线和圆的位置关系
l
l
l



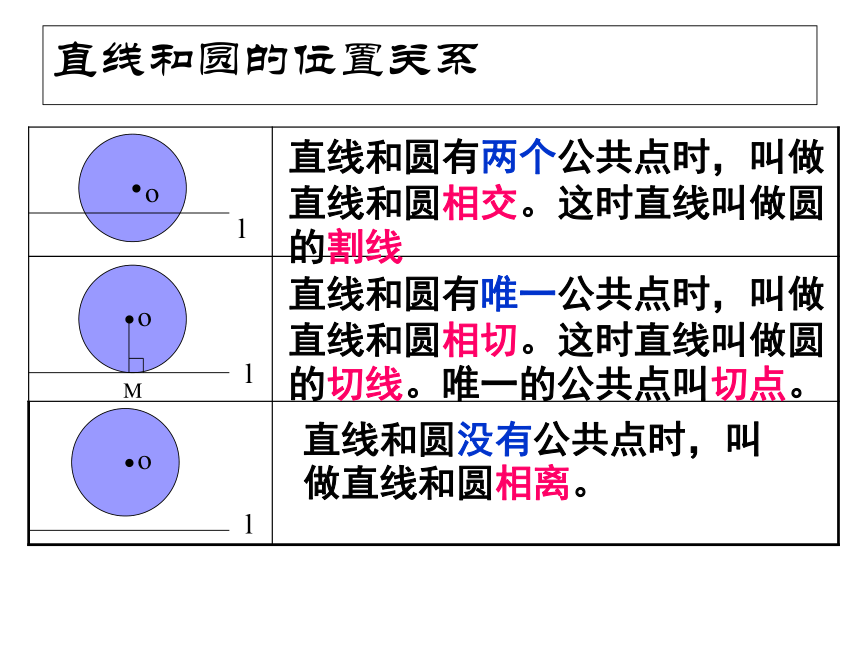
直线和圆有两个公共点时，叫做直线和圆相交。这时直线叫做圆的割线
直线和圆有唯一公共点时，叫做直线和圆相切。这时直线叫做圆的切线。唯一的公共点叫切点。
直线和圆没有公共点时，叫做直线和圆相离。
o
o
o
M
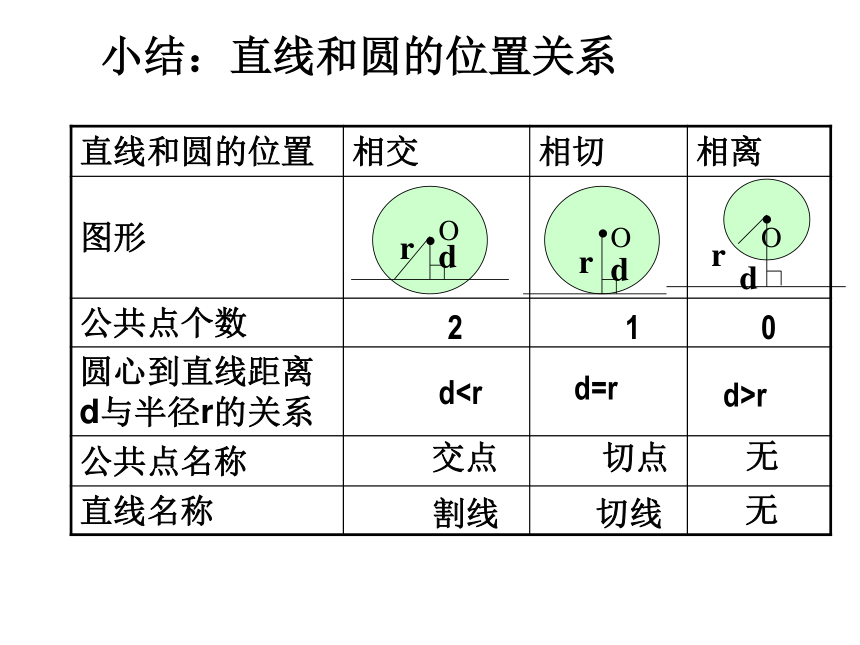
小结：直线和圆的位置关系
直线和圆的位置 相交 相切 相离
图形
公共点个数
圆心到直线距离 d与半径r的关系
公共点名称
直线名称
2
1
0
dd=r
d>r
交点
切点
无
割线
切线
无
O

d
r
O
l

d
r
O

d
r
总结：
判定直线与圆的位置关系的方法有____种：
（1）根据定义，由___________
的个数来判断；
（2）根据性质，由______________ ______________的关系来判断。
两
直线 与圆的公共点
圆心到直线的距离d
与半径r
切线的判定方法有：
③ 切线的判定定理。
② 直线到圆心的距离等于圆的半径。
① 直线与圆有一个公共点。
切线的判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线。
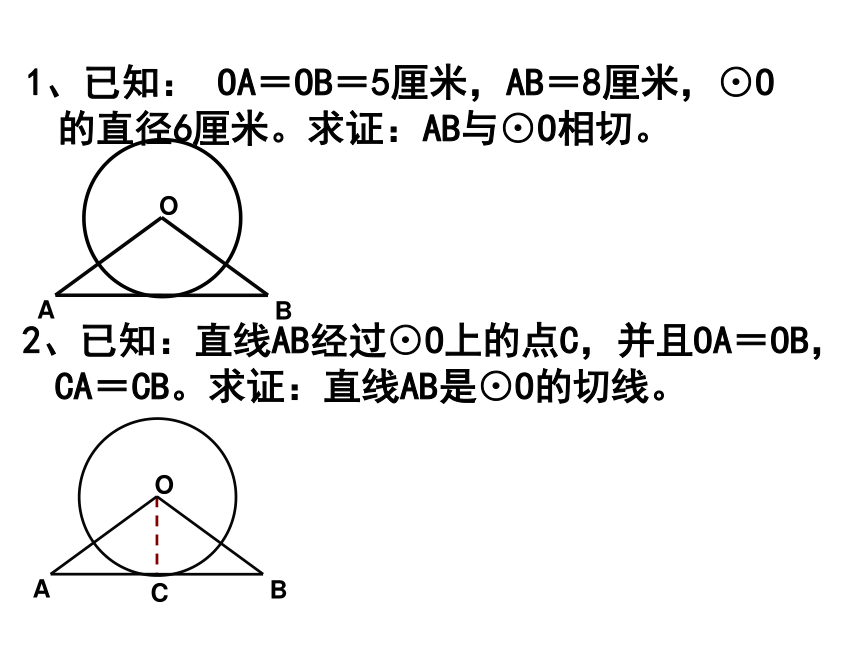
2、已知：直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB。求证：直线AB是⊙O的切线。
O
C
B
A
1、已知： OA＝OB＝5厘米，AB＝8厘米，⊙O的直径6厘米。求证：AB与⊙O相切。
O
B
A
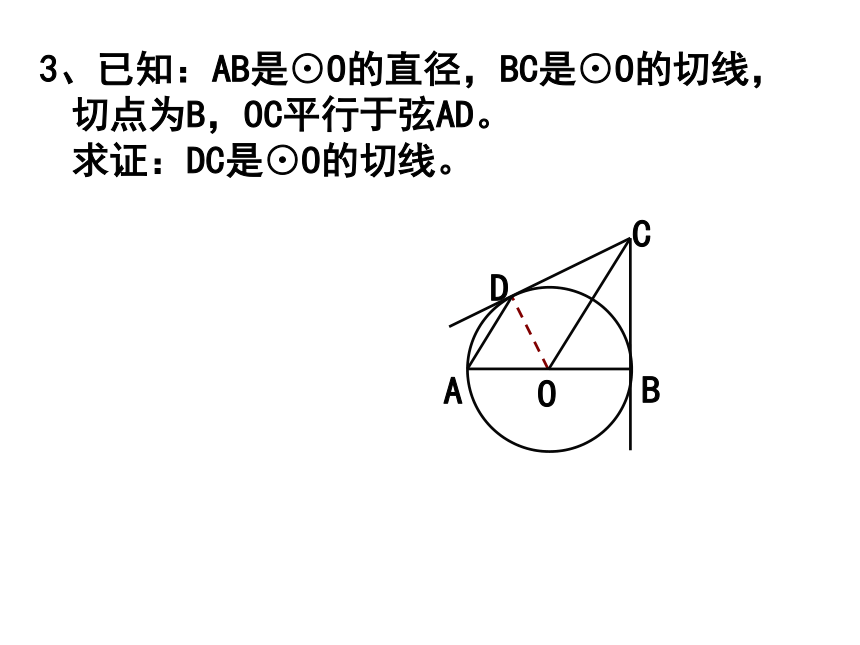
3、已知：AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD。 求证：DC是⊙O的切线。
D
C
O
B
A
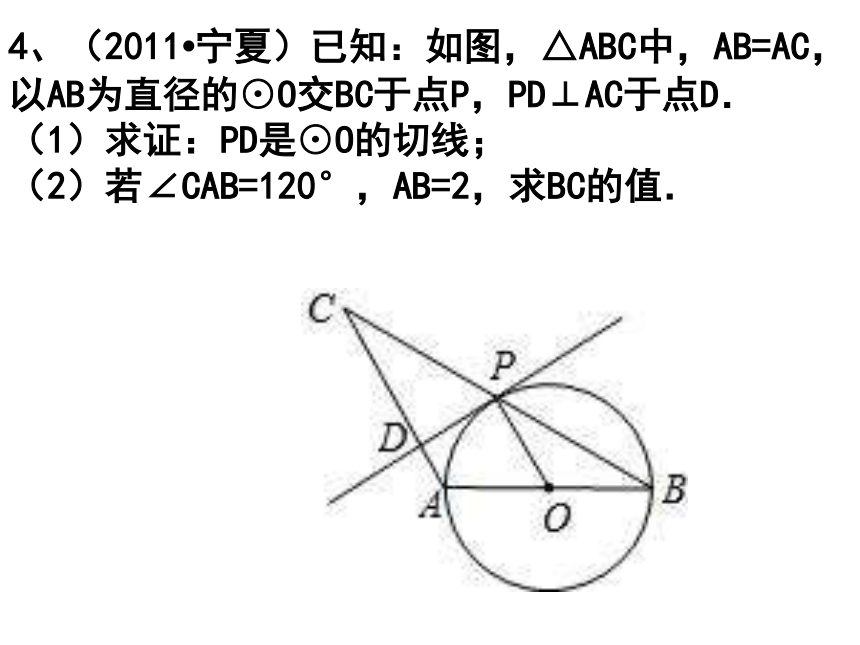
4、（2011 宁夏）已知：如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点P，PD⊥AC于点D．
（1）求证：PD是⊙O的切线；
（2）若∠CAB=120°，AB=2，求BC的值．
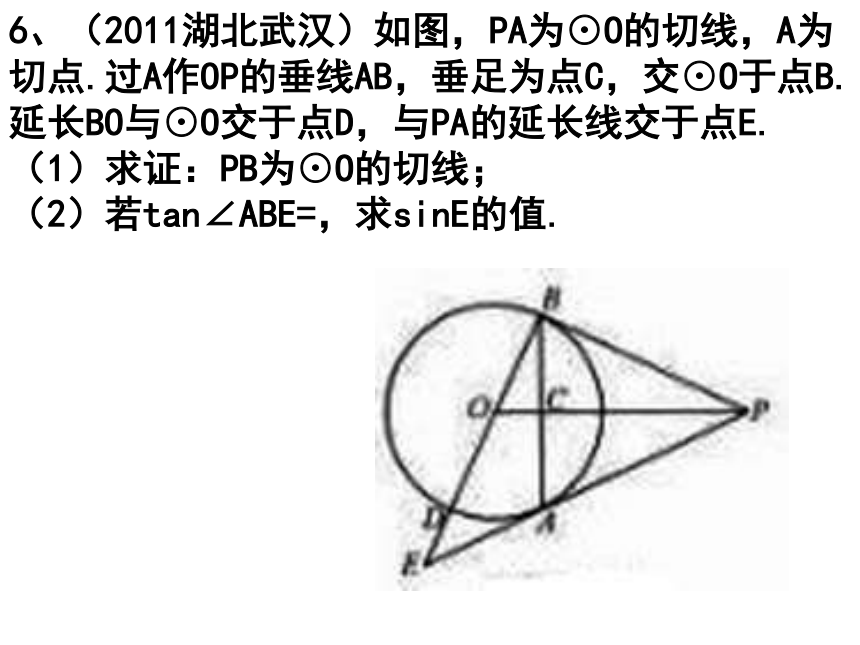
6、（2011湖北武汉）如图，PA为⊙O的切线，A为切点.过A作OP的垂线AB，垂足为点C，交⊙O于点B.延长BO与⊙O交于点D，与PA的延长线交于点E.
（1）求证：PB为⊙O的切线；
（2）若tan∠ABE=，求sinE的值.
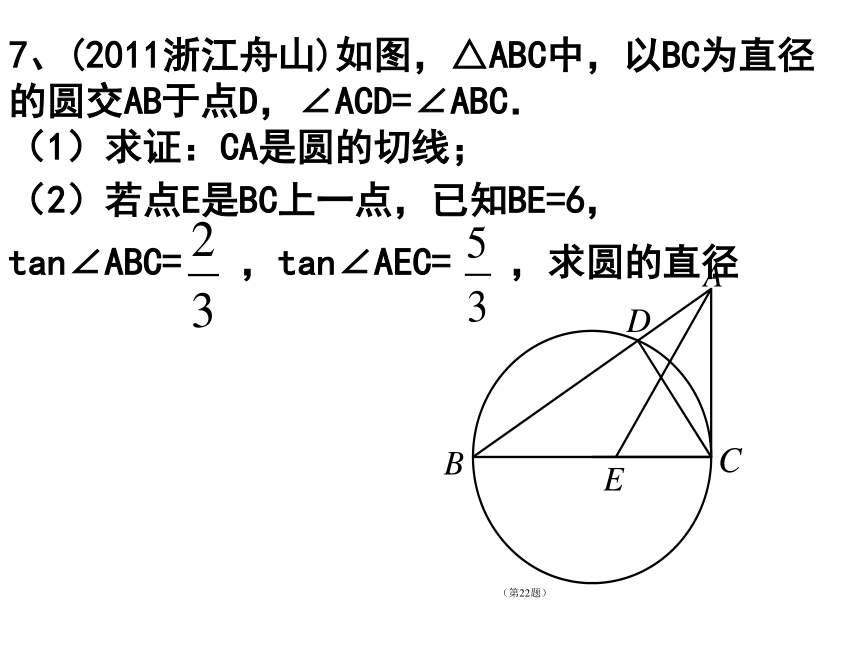
7、(2011浙江舟山)如图，△ABC中，以BC为直径的圆交AB于点D，∠ACD=∠ABC．
（1）求证：CA是圆的切线；
（2）若点E是BC上一点，已知BE=6，
tan∠ABC= ，tan∠AEC= ，求圆的直径
（第22题）
1、经过切点的半径垂直于圆的切线。
3、经过圆心垂直于切线的直线必过切点。
2、经过切点垂直于切线的直线必过圆心。
切线的判定和性质可归纳为：已知满足
1、过圆心，2、过切点，3、垂直于切线，中任意两个，便得到第三个结论。
１、如图, ⊙O切PB于点B,PB=4,PA=2,则
⊙O的半径多少？
2、 如图：PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___
3、如图，在RTΔABC中，∠C=90°，AC=3，BC=4，以BC上一点O为圆心作⊙O与AC、AB都相切，设⊙O与BC的另一个交点为D，求线段BD的长度？
A
C
B
D
O
E
4、（2011 陕西）如图，在△ABC中，∠B=60°，⊙O是△ABC外接圆，过点A作⊙O的切线，交CO的延长线于P点，CP交⊙O于D
（1）求证：AP=AC；
（2）若AC=3，求PC的长．
5、（2011年青海）已知：AB是⊙O的直径，AC是弦，直线EF是过点C的⊙O的切线，AD⊥EF于点D.
（1）求证：∠BAC=∠CAD
（2）若∠B=30°，AB=12，求的长.
(3) 若DA＝4cm，CD＝8cm，求⊙O的面积。
6、如图：已知PA，PB分别切⊙O于A，B两点，如果∠P=60° ，PA=2，那么AB的长为_____.
2
变式1:CD也与⊙O相切,切点为E.交PA于C点，交PB于D点，则△ PCD的周长为____.
4
E
C
D
变式2:改变切点E的位置(在略户ＡＢ上)，则△ PCD的周长为____.
变式３：若PA=５则△ PCD的周长为____.
４
１０
变式４：若PA=a,则△ PCD的周长为____.
2a
三角形的内切圆

外心

名称
确定方法
图形
性质














（三角形外接
圆的圆心）
（三角形内切
圆的圆心）
三角形三边
中垂线的交点
三角形三条
角平分线的
交点
内心
(1)OA=OB=OC
（2）外心不一定
在三角形的内部．
（1）到三边的距离相等；
（2）OA、OB、OC分别平分∠BAC、∠ABC、∠ACB；
（3）内心在三角形内部．
O
I
特殊三角形外接圆、内切圆半径的求法：
R= —
c
2
r = ————
a+b-c
2
A
B
C
a
b
c
直角三角形外接圆、内切圆半径的求法
等边三角形外接圆、 内切圆半径的求法
基本思路：
构造三角形BOD，BO为外接圆半径，DO为内切圆半径。
A
B
C
O
D
R
r
如图，在ΔABC中，AC=6，BC=8，AB=10，求ΔABC内切圆的半径.
C
A
B
D
E
F
O
1、正三角形边长为6，求它的内切圆半径及外接圆的半径
2、正三角形内切圆半径为6，求它的边长及外接圆的半径
3、正三角形外接圆的半径为6，求它的边长及内切圆半径
4、如图，在ΔABC中，AC=BC，E是内心，AE的延长线交ΔABC的外接圆于D
求证：（1）BE=AE
A
B
C
E
D
圆和圆的位置关系
两个圆没有公共点，并且每个圆上的点都在另一个圆的外部。
两个圆没有公共点，并且每个圆上的点都在另一个圆的内部。
d>R+r
dd
R
r
O1
O2
d
R
r
O1
O2
两个圆有唯一公共点，并且除这公共点外，每个圆上的点都在另一个圆的外部。
两个圆有唯一公共点，并且除这公共点外，每个圆上的点都在另一个圆的内部。
d=R+r
d=R-r
d
R
r
O1
O2
d
R
r
O1
O2
两个圆有两个公共点。
R-rd
R
r
O1
O2
从公共点个数看两圆位置关系
公共点个数
没有公共点
（相离）
一个公共点
（相切）
两个公共点
（相交）
外离
内含
外切
内切
两圆位置关系的数量特征
d：圆心距
R、r：两圆半径（R>r）
内含
相交
外离
R＋r外切
R－r内切
外离
圆和圆的五种位置关系
O1O2>R+r
O1O2=R+r
R-rO1O2=R-r
0≤O1O2O1O2=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
如果两圆相切，那么切点在连心线上。
相切两圆的性质
相交两圆的连心线垂直平分公共弦。
相交两圆的性质
1.若半径为7和9的两圆相切,则这两圆的圆心距长一定为( )
A.16 B.2 C.2或16 D.以上均不对
2.若半径为1和5的两圆相交,则圆心距d的取值范围为( )
A.d＜6 B. 4＜ d ＜6 C.4≤d≤6 D.1＜d＜5
3.若两圆半径为6cm和4cm,圆心距为10cm,那么这两圆的位置关系为( )
A.内切 B.相交 C.外切 D.外离
C
B
C
4.已知两圆的半径为R和r(R＞r), 圆心距为d ,且
则两圆的位置关系为( )
A.外切 B. 内切 C.外离 D.外切或内切
D
5.两圆相切,圆心距等于3,一个圆的半径为5cm,则另一个圆的半径为 .
6.两个等圆⊙O1和⊙O2相交于A,B两点, ⊙O1经过点O2,则∠O1AB的度数为 .
7.已知两圆的圆心距为5,⊙O1和⊙O2的半径分别是方程 的两根,则两圆的关
系为 .
8.两圆的半径为5和3,且两圆无公共点,则两圆圆心距d的取值范围为 .
2cm或8cm
30°
内切
d＞8或d＜2
10、⊙O1和⊙O2相切于点P,过点P的直线交于⊙O1点A,交⊙O2于点B,求证: O1A∥O2B
本题要分两种情况讨论:
一是两圆外切时,
二是两圆内切时.
11、设⊙p的半径为4cm，直线l上一点A到圆心的距离为4cm，则直线l与⊙P的位置关系是（ ）
A、相交 B、相切 C、相离 D、相切或相交
D
12、如图，PC切⊙O于点C,PC=4cm，PO=6cm,
求⊙O的半径。
变式：
若PC切⊙O于点C,延长PO交⊙O于A、B两点，AB=2PA.
（1）求∠P的正弦.
（2） 连结BC，你还能得到什么结论？
（3)若过点P作∠CPB的平分线交BC于点M，求∠CMP的度数。
(4)若点P在直径BA的延长线上运动（PC仍为切线），∠CMP的大小是否发生变化？试说明理由。
若PC切⊙O于点C,延长PO交⊙O于A、B两点，AB=2PA
13、（湖北襄阳）如图AB在x轴上，AB=10，以AB为直径的⊙O‘与y轴正半轴交于点C，连接BC，AC。CD是⊙O’的切线，AD丄CD于点D，tan∠CAD= ，抛物线y=ax2+bx+c过A，B，C三点．
（1）求证：∠CAD=∠CAB；
（2）①求抛物线的解析式；
②判断抛物线的顶点E
是否在直线CD上，并
说明理由；
（3）在抛物线上是否
存在一点P，使四边形
PBCA是直角梯形．若
存在，直接写出点P的
坐标（不写求解过程）；若不存在，请说明理由．