1.1 二次函数课件（36张）

(共36张PPT)
篮球运行的路线是什么曲线？
怎样出手才能把球投进篮圈？
起跳多高才能成功盖帽？等
请用适当的函数解析式表示下列问题情境中的两个变量
y
与
X
之间的关系：
(1)圆的面积
y
(
)与圆的半径
x
(
cm
)
独立思考：
（2）菱形的两条对角线长的和为26cm，其中一条对角线长为xcm，菱形面积为y
银行的储蓄利率是随时间的变化而变化的，也就是说，利率是一个变量。在我国，利率的调整是由中国人民银行根据国民经济发展的情况而决定的。
利率
本金
利息
本息
合作学习：
＝
×
＝
＋
(3)王先生存入银行2万元,先存一个一年定期，一年后银行将本息自动转存为又一个一年定期,设一年定
期的年利率为
x，
两年后王先生共得本息y元;
请用适当的函数解析式表示下列问题情境中的两个变量
y
与
X
之间的关系：
合作学习：
(4)拟建中的一个温室的平面图如图,如果温室外围是一个矩形，周长为120m
,
室内通道的尺寸如图,设一条边长为
x
(m),
种植面积为
y
(m2)·
种植面积
通道
合作学习：
上述四个问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax?+bx+c
的形式.
(a,b,c是常数,
)
a≠0
二次函数的一般形式:
y＝ax2＋bx＋c
(其中a、b、c是常数,a≠0)
a是二次项系数
b是一次项系数
C是常数项
二次函数的特殊形式：
当b＝0时，
y＝ax2＋c
当c＝0时，
y＝ax2＋bx
当b＝0，c＝0时，
y＝ax2
定义：
一般地，形如y=ax?+bx+c(a,b,c是常数,a≠
0)的函数叫做x的二次函数。
（1）等号左边是变量y，右边是关于自变量x的
（3
）等式的右边最高次数为
，可以没有一次项和常数项，但不能没有二次项。
注意：
（2）a,b,c为常数，且
（4）x的取值范围是
。
整式
a≠0.
2
任意实数
注意:当二次函数表示某个实际问题时,还必须根据题意确定自变量的取值范围.
二次函数的解析式y=ax?+bx+c
(其中a,b,c是常数，a≠0)
想一想:函数的自变量x是否可以取任何值呢?
例1、下列函数中，哪些是二次函数？若是,分别指出二次项系数,一次项系数,常数项.
(1)
y=3(x-1)?+1
(2)
y=x+
(3)
s=3-2t?
(4)
y=(x+3)?-x?
(5)y=
-x
(6)
v=10π
r?
1
x
__
x?
1
__
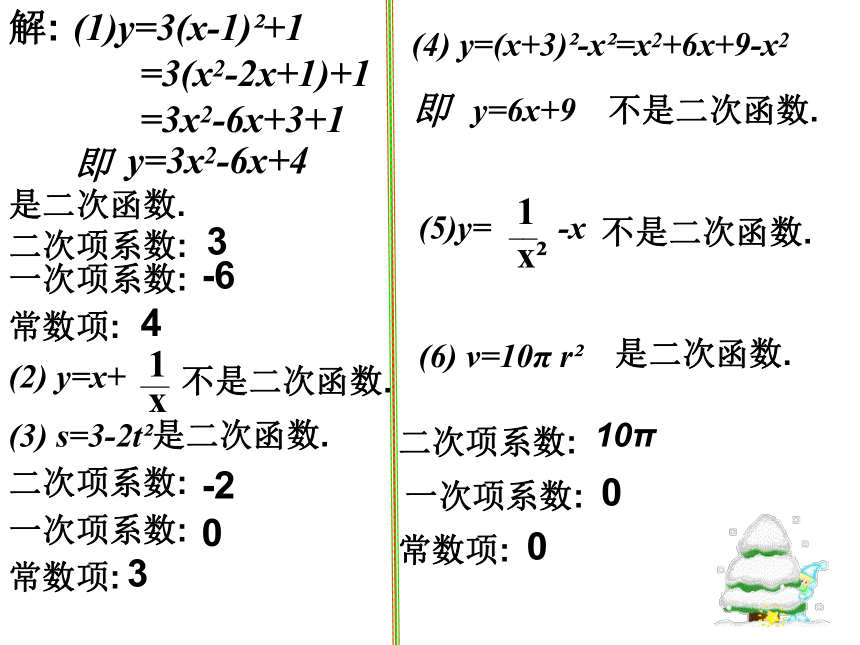
解:
y=3(x-1)?+1
=3(x2-2x+1)+1
=3x2-6x+3+1
即
y=3x2-6x+4
是二次函数.
二次项系数:
一次项系数:
常数项:
3
-6
4
(2)
y=x+
1
x
__
不是二次函数.
(3)
s=3-2t?是二次函数.
二次项系数:
一次项系数:
常数项:
-2
0
3
(4)
y=(x+3)?-x?=x2+6x+9-x2
即
y=6x+9
不是二次函数.
二次项系数:
一次项系数:
常数项:
10π
0
0
不是二次函数.
(5)y=
-x
x?
1
__
(6)
v=10π
r?
是二次函数.
一次函数y=ax+b
(a
≠0),其中包括正比例函数y=kx(k≠0),
反比例函数y=
(k≠0)
二次函数y=ax2+bx+c(a≠0).
现在我们学习过的函数有:
可以发现,这些函数的名称都反映了函数表达式与自变量的关系.
函数解析式
二次项系数a
一次项系数b
常数项
c
0
0
2
4
2
－1
58
－112
13
0
1.说出下列二次函数的二次项系数、一次项系数和常数项：
试一试:
二次函数y=ax?+bx+c中a≠0,但b、c可以为0.
2.下列函数中,哪些是二次函数？是二次函数的，请说出它的二次项系数、一次项系数和常数项：
是
不是，因为不是整式
3.函数
当m取何值时，
（1）它是二次函数？
（2）它是反比例函数？
（1）若是二次函数，则
且
∴当
时，是二次函数。
（2）若是反比例函数，则
且
∴当
时，是反比例函数。
4.函数
（其中a、b、c为常数），当a、b、c满足什么条件时，
（1）它是二次函数；
（2）它是一次函数；
（3）它是正比例函数；
当
时，是二次函数；
当
时，是一次函数；
当
时，是正比例函数；
例2
如图，一张正方形纸板的边长为2cm，将它剪去4个全等
的直角三角形
(图中阴影部分
)。设AE＝BF＝CG＝DH＝x(cm)，四边形
EFGH的面积为y(cm2)
求
（1）y关于
x的函数解析式和自变量x的取值范围
;
（2）当
x分别为0.25，0.5，1，1.5，1.75时
，对应的四边形
EFGH的面积，并列表表示.
X
X
X
X
2–X
2–X
2–X
2–X
例题讲解：
直接法
求
（1）y关于
x的函数解析式和自变量x的取值范围
;
X
X
X
X
2–X
2–X
2–X
2–X
例题讲解：
解：由题意，得
分析:S四边形EFGH＝S正方形ABCD－4×SRt△AEH
求
（1）y关于
x的函数解析式和自变量x的取值范围
;
X
X
X
X
2–X
2–X
2–X
2–X
例题讲解：
求差法
解：∵△AEH≌△BFE≌△CGF≌△DHG
∴EH＝FE＝GF＝HG
∴四边形EFGH为菱形
∵∠AEH＝∠BFE
∵∠BFE＋∠BEF＝90°
∴∠AEH＋∠BEF＝90°
即∠HEF＝90°
∴菱形EFGH为正方形
1
求
（1）y关于
x的函数解析式和自变量x的取值范围
;
X
X
X
X
2–X
2–X
2–X
2–X
例题讲解：
求差法
解：∵△AEH≌△BFE≌△CGF≌△DHG
∴EH＝FE＝GF＝HG
∴四边形EFGH为菱形
∵∠AEH＝∠BFE
∵∠BFE＋∠BEF＝90°
∴∠AEH＋∠BEF＝90°
即∠HEF＝90°
∴菱形EFGH为正方形
求
（2）当
x分别为0.25，0.5，1，1.5，1.75时
，对应的四边形
EFGH的面积，并列表表示.
例题讲解：
0.25
0.5
1
1.5
1.75
3.125
2.5
2
2.5
3.125
列表如下：
x
用20米的篱笆围一个矩形的花圃（如图），
设连墙的一边为x,矩形的面积为y,
求：(1)
写出y关于x的函数关系式.
(2)
当x=3时,矩形的面积为多少?
(2)当x=3时
试一试:
(0答：当x＝3时，矩形的面积为42m2。
例3:已知二次函数y=x?+px+q,当x=1时,函数值为4,当x=2时,函数值为-
5,
求这个二次函数的解析式.
待定系数法
例题讲解：
　　已知二次函数y=ax?+bx+3,
当x=2时,函数值为3,
当x=
-
2时,
函数值为2,
求这个二次函数的解析式.
　
做一做
这节课你有什么收获？
这节课你还有什么困惑？
1、二次函数的概念：形如
2、a为二次项系数、b为一次项系数、c为常数项
3、用待定系数法求二次函数的解析式
4、二次函数与一次函数、正比例函数、反比例函数的区别
拓展提高
1.
4
x
x
4-x
AE=EF
42+(4-x)2=2x2
2.大润发超市进了一批成本为8元/个的文具盒。调查发现：这种文具盒每个星期的销售量y（个）与它的定价x（元/个）的关系如图所示：
（1）求这种文具盒每个星期的销售量y（个）与它的定价x
（元/个）之间的函数关系式（不必写出自变量x的取值范围）；
（2）设超市每星期的利润为w(元)
，求超市每星期的利润W（元）
与文具盒的定价x
（元/个）之间的函数表达式。
拓展提高
y＝－10x＋300
W＝
(x-8)(-10x＋300)?=-10x2+380x-2400
温馨提示：同桌交对，互相帮助！
知识拓展：
心理学家研究发现：一般情况下，学生的注意力随着教师讲课时间的变化而变化，讲课开始时，学生的注意力y随时间t的变化规律有如下关系式：
（1）讲课开始后第5分钟时与讲课开始后第25分钟时比较，何时学生的注意力更集中？
（2）讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？
（3）一道数学难题，需要讲解24分钟，为了效果较好，要求学生的注意力最低达到180，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？
　　大家收获不小吧！说说你的感受，让大家一起来分享，怎么样？
我掌握了……
我学会了……
我体会到了……
我还有……疑问.
1、下列函数中，（x是自变量），是二次函数的为(
)
A
y=ax2+bx+c
B
y2=x2-4x+1
C
y=x2
D
y=2+
√x2+1
2.函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
A
m,n是常数,且m≠0
B
m,n是常数,且n≠0
C
m,n是常数,且m≠n
D
m,n为任何实数
C
C
1.一个圆柱的高等于底面半径,写出它的表面积
s
与半径
r
之间的关系式.
当r为4时s为多少。
2.
n支球队参加比赛,每两队之间进行一场比赛,写出比赛的场次数
m与球队数
n
之间的关系式.
S=4πr2
即
3.将进货单价为40元的商品按50元卖出时,就能卖出500个,已知这种商品每涨1元,其销售量就会减少10个,设售价定为X元(x＞50)时的利润为Y元。试求出Y与X的函数关系式，并按所求的函数关系式计算出售定价为80元时所得利润。
例4、若二次函数y＝2x2＋bx＋c的图形经过A（－1，0），B（0，1），二点，求这个函数的解析式.
二次函数
，
当x=0时，y=-2；当y=-2时，x=0，求y=2时，x的值。
函数解析式
系数
自变量的
最高次数
课本P
28---29
页作业题
作业：