1.2二次函数的图象 ( 1 )课件(21张)
文档属性
| 名称 | 1.2二次函数的图象 ( 1 )课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-15 18:18:12 | ||
图片预览






文档简介
(共21张PPT)
课程标准浙教版实验教科书
九年级
上
册
数
学
1.2
二次函数的图象(1)
回顾知识:
一、正比例函数y=kx(k
≠
0)的图象是什么.
二、一次函数y=kx+b(k
≠
0)的图象又是什么.
正比例函数y=kx(k
≠
0)其图象是一条经过原点的直线.
一次函数y=kx+b(k
≠
0)其图象也是一条直线.
反比例函数
(k
≠
0)其图象是双曲线.
三、反比例函数
(k
≠
0)的图象又是什么.
二次函数y=ax?+
bx+c(a
≠
0)的图象又是什么呢?.
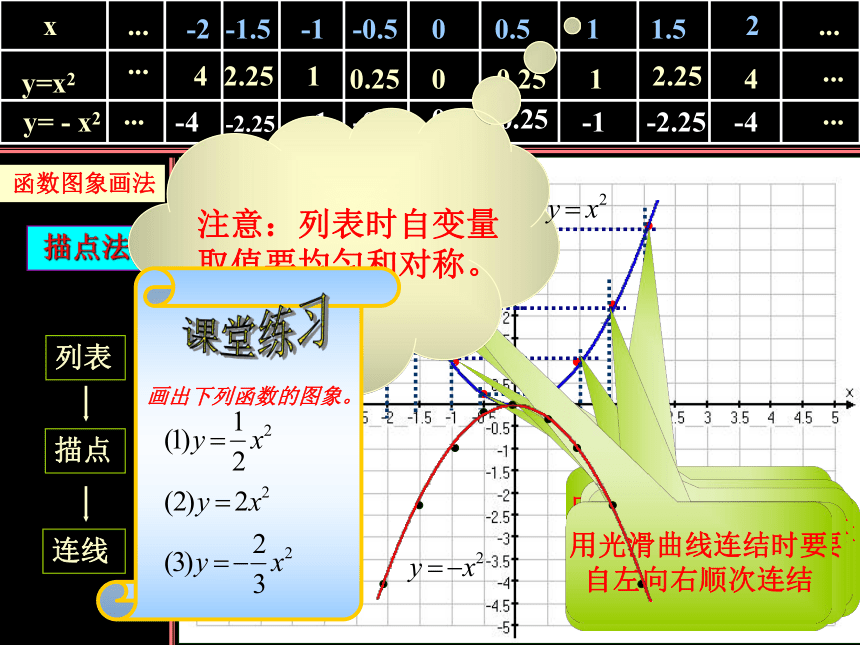
二次函数y=ax2的图像
x
y=x2
y=
-
x2
...
...
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
函数图象画法
列表
描点
连线
0
0.25
1
2.25
4
0.25
1
2.25
4
描点法
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
注意:列表时自变量
取值要均匀和对称。
课堂练习
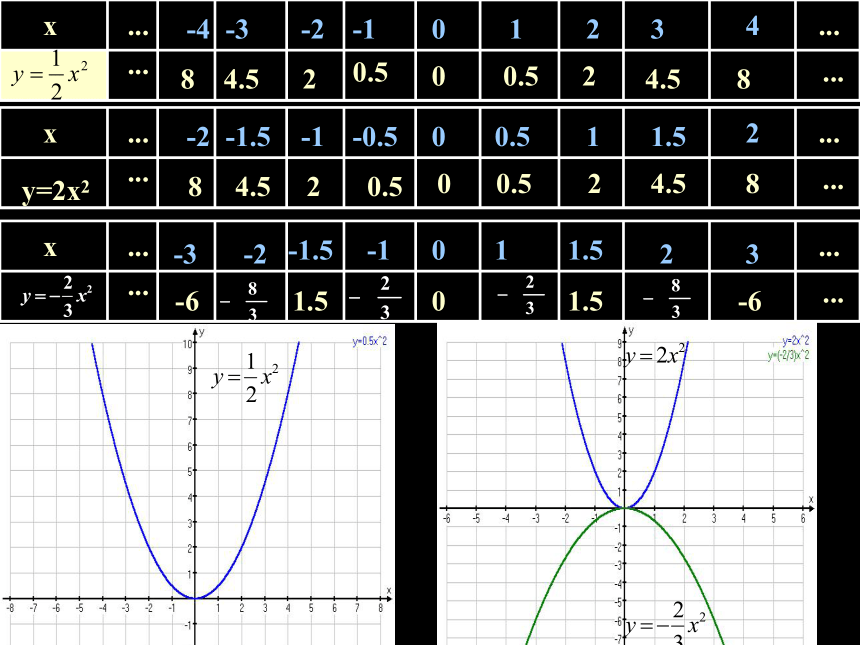
画出下列函数的图象。
x
y=2x2
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
x
y=x2
...
...
...
...
0
-4
-3
-2
-1
2
3
1
4
0
0.5
2
4.5
8
0.5
2
4.5
8
列表参考
0
0.5
2
4.5
8
0.5
2
4.5
8
x
...
...
...
...
0
-3
-1.5
-1
1.5
1
-2
2
3
0
1.5
-6
1.5
-6
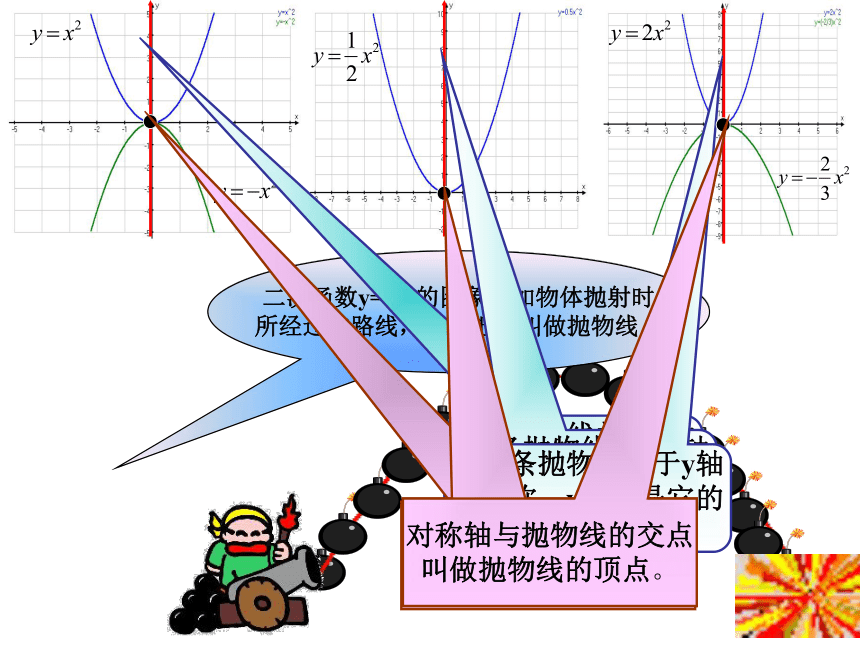
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
欣赏生活中的抛物线
焰火
抛物线
y=x2
y=-x2
顶点坐标
对称轴
位置
开口方向
极值
课堂练习
1、观察右图,
并完成填空。
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0。
当x=0时,最大值为0。
小结
二次函数y=ax2的性质
1、顶点坐标与对称轴
2、位置与开口方向
3、极值
2、练习2
在同一坐标系内,抛物线y=x2与抛物线
y=
-x2的位置有什么关系?
如果在同一坐标系内
画函数y=ax2与y=
-ax2的图象,怎样画才简便?
答:抛物线抛物线y=x2与抛物线
y=
-x2
既关于x轴对称,
又关于原点对称。只要画出y=ax2与y=
-ax2中的一条抛物线,
另一条可利用关于x轴对称或关于原点对称来画。
1、抛物线y=ax2的顶点是原点,对称轴是y轴。
2、当a>0时,抛物线y=ax2在x轴的
上方(除顶点外),它的开口向上,并且向上无限伸展,当x=0时函数y的值最小;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展,当x=0时,函数y的值最大。
二次函数y=ax2的性质
直线x=0
1、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,-
4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解(1)把(-2,-8)代入y=ax2,得-8=a(-2)2,
解出a=
-2,所求函数解析式为y=
-2x2.
(2)因为当x=-1时,y=-2x2
=-2×(-1)2=-2≠-4
所以点B(-1
,-4)不在此抛物线上。
(3)由-6=-2x2
,得x2=3,
所以纵坐标为-6的点有两个,它们分别是
y=-2x2
若抛物线y=ax2(a≠0),过点(-1,3)。
(1)a的值是______;
(2)对称轴是_______,开口_______。
(3)顶点坐标是______,顶点是抛物线上的________。抛物线在x轴的____方(除顶点外)
练一练:
y轴
向上
(0,0)
最低点
上
谈收获:
1.二次函数y=ax2(a≠0)的图像是一条抛物线.
2.图象关于y轴对称,顶点是坐标原点.
3.当a>0时,抛物线的开口向上,顶点是抛物线上的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点.
1,已知抛物线y=ax2经过点(-2,2).
(1)
求这条抛物线的解析式.
(2)
求出这个二次函数的最大值或最小值.
(3)
在此抛物线上有两点A(x1,y1),B(x2,y2),
且
x1>x2>0,试比较y1与y2的大小.
拓展训练
(4)若在此抛物线上有两点A(2,y1),B(-2,y2),试比较y1与y2的大小.
(5)若在此抛物线上有两点A(2,y1),B(-1,y2),试比较y1与y2的大小.
.
.
y1>y2
y1=y2
y2>y1
2.某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图
所示,栅栏的跨径AB,按相同的间距0.2米用5根立柱加
固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建
立平面直角坐标系,根据以上的数据,则这段栅栏所需立
柱的总长度(精确到0.1米)为______
拓展提高
.
.
拓展提高
课本P
31---32
页作业题
再见
作业:
课程标准浙教版实验教科书
九年级
上
册
数
学
1.2
二次函数的图象(1)
回顾知识:
一、正比例函数y=kx(k
≠
0)的图象是什么.
二、一次函数y=kx+b(k
≠
0)的图象又是什么.
正比例函数y=kx(k
≠
0)其图象是一条经过原点的直线.
一次函数y=kx+b(k
≠
0)其图象也是一条直线.
反比例函数
(k
≠
0)其图象是双曲线.
三、反比例函数
(k
≠
0)的图象又是什么.
二次函数y=ax?+
bx+c(a
≠
0)的图象又是什么呢?.
二次函数y=ax2的图像
x
y=x2
y=
-
x2
...
...
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
函数图象画法
列表
描点
连线
0
0.25
1
2.25
4
0.25
1
2.25
4
描点法
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
0
-0.25
-1
-2.25
-4
-0.25
-1
-2.25
-4
注意:列表时自变量
取值要均匀和对称。
课堂练习
画出下列函数的图象。
x
y=2x2
...
...
...
...
0
-2
-1.5
-1
-0.5
1
1.5
0.5
2
x
y=x2
...
...
...
...
0
-4
-3
-2
-1
2
3
1
4
0
0.5
2
4.5
8
0.5
2
4.5
8
列表参考
0
0.5
2
4.5
8
0.5
2
4.5
8
x
...
...
...
...
0
-3
-1.5
-1
1.5
1
-2
2
3
0
1.5
-6
1.5
-6
二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
这条抛物线关于y轴
对称,y轴就是它的
对称轴。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
对称轴与抛物线的交点
叫做抛物线的顶点。
欣赏生活中的抛物线
焰火
抛物线
y=x2
y=-x2
顶点坐标
对称轴
位置
开口方向
极值
课堂练习
1、观察右图,
并完成填空。
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0。
当x=0时,最大值为0。
小结
二次函数y=ax2的性质
1、顶点坐标与对称轴
2、位置与开口方向
3、极值
2、练习2
在同一坐标系内,抛物线y=x2与抛物线
y=
-x2的位置有什么关系?
如果在同一坐标系内
画函数y=ax2与y=
-ax2的图象,怎样画才简便?
答:抛物线抛物线y=x2与抛物线
y=
-x2
既关于x轴对称,
又关于原点对称。只要画出y=ax2与y=
-ax2中的一条抛物线,
另一条可利用关于x轴对称或关于原点对称来画。
1、抛物线y=ax2的顶点是原点,对称轴是y轴。
2、当a>0时,抛物线y=ax2在x轴的
上方(除顶点外),它的开口向上,并且向上无限伸展,当x=0时函数y的值最小;
当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展,当x=0时,函数y的值最大。
二次函数y=ax2的性质
直线x=0
1、已知抛物线y=ax2经过点A(-2,-8)。
(1)求此抛物线的函数解析式;
(2)判断点B(-1,-
4)是否在此抛物线上。
(3)求出此抛物线上纵坐标为-6的点的坐标。
解(1)把(-2,-8)代入y=ax2,得-8=a(-2)2,
解出a=
-2,所求函数解析式为y=
-2x2.
(2)因为当x=-1时,y=-2x2
=-2×(-1)2=-2≠-4
所以点B(-1
,-4)不在此抛物线上。
(3)由-6=-2x2
,得x2=3,
所以纵坐标为-6的点有两个,它们分别是
y=-2x2
若抛物线y=ax2(a≠0),过点(-1,3)。
(1)a的值是______;
(2)对称轴是_______,开口_______。
(3)顶点坐标是______,顶点是抛物线上的________。抛物线在x轴的____方(除顶点外)
练一练:
y轴
向上
(0,0)
最低点
上
谈收获:
1.二次函数y=ax2(a≠0)的图像是一条抛物线.
2.图象关于y轴对称,顶点是坐标原点.
3.当a>0时,抛物线的开口向上,顶点是抛物线上的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点.
1,已知抛物线y=ax2经过点(-2,2).
(1)
求这条抛物线的解析式.
(2)
求出这个二次函数的最大值或最小值.
(3)
在此抛物线上有两点A(x1,y1),B(x2,y2),
且
x1>x2>0,试比较y1与y2的大小.
拓展训练
(4)若在此抛物线上有两点A(2,y1),B(-2,y2),试比较y1与y2的大小.
(5)若在此抛物线上有两点A(2,y1),B(-1,y2),试比较y1与y2的大小.
.
.
y1>y2
y1=y2
y2>y1
2.某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图
所示,栅栏的跨径AB,按相同的间距0.2米用5根立柱加
固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建
立平面直角坐标系,根据以上的数据,则这段栅栏所需立
柱的总长度(精确到0.1米)为______
拓展提高
.
.
拓展提高
课本P
31---32
页作业题
再见
作业:
同课章节目录
