3.3 垂径定理（1）课件（21张）

(共21张PPT)
请观察下列三个银行标志有何共同点?
圆的对称性
圆是轴对称图形吗？
如果是,它的对称轴是什么?你能找到多少条对称轴？
●O
你是用什么方法解决上述问题的?
圆的对称性
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
注意：
对称轴是直线，不能说每一条直径都是它的对称轴；
(1)该图是轴对称图形吗？
(2)能不能通过改变AB、CD的位置关系,使它成为轴对称图形?
直径CD和弦AB互相垂直
如图,AB是⊙O的一条弦,CD是⊙O直径.
特殊情况
在⊙O中，AB为弦，
CD为直径,CD⊥AB
提问：你在图中能找到哪些相等的量？并证明你猜想的结论。
M
B
A
O
C
D
如图,小明的理由是:
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB，OM=OM，
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC
=BC,
⌒
⌒
　AD
=BD.
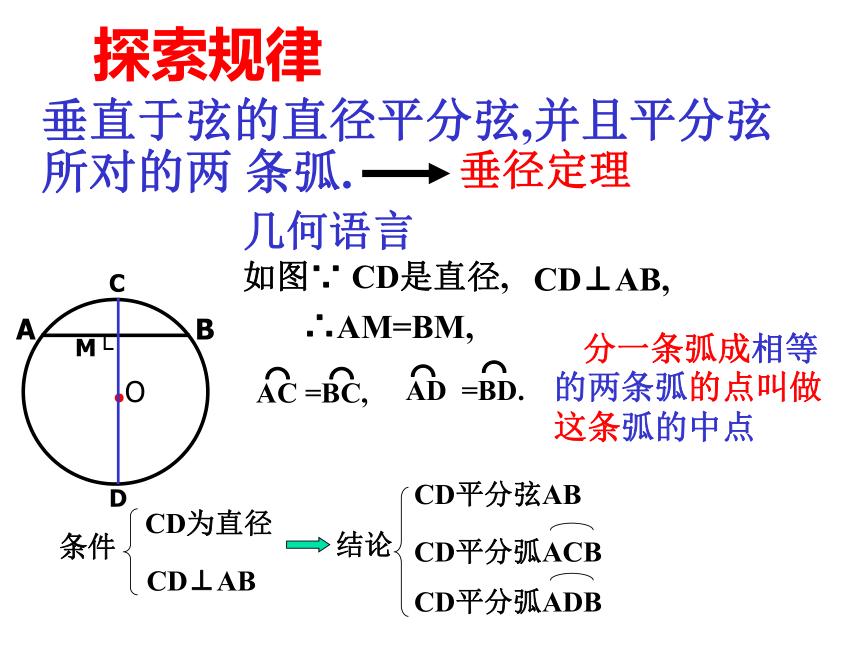
探索规律
能够重合的弧叫等弧
垂直于弦的直径平分弦,并且平分弦所对的两
条弧.
●O
A
B
C
D
M└
CD⊥AB,
几何语言
如图∵
CD是直径,
∴AM=BM,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
条件
CD为直径
CD⊥AB
CD平分弧ADB
CD平分弦AB
CD平分弧ACB
结论
探索规律
分一条弧成相等的两条弧的点叫做这条弧的中点
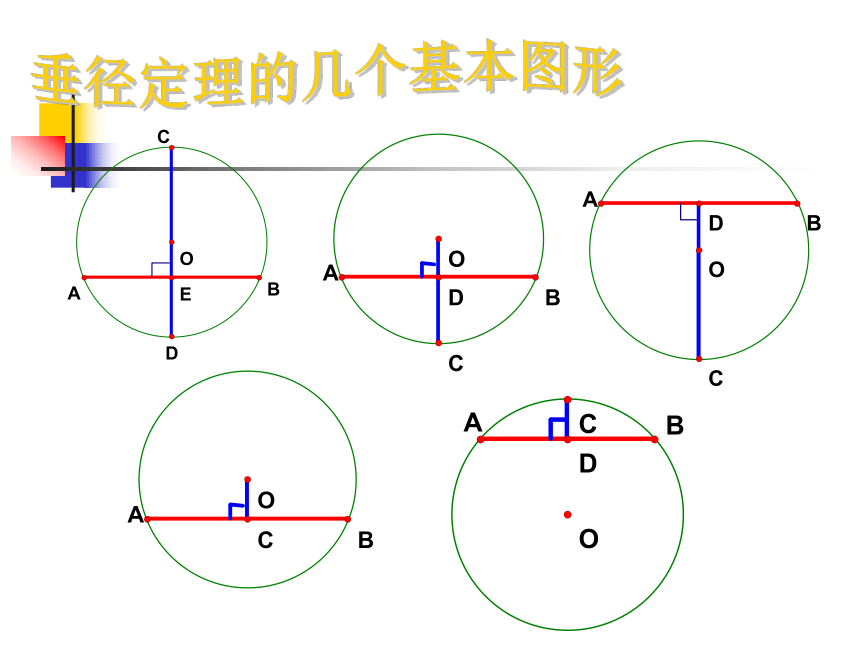
垂径定理
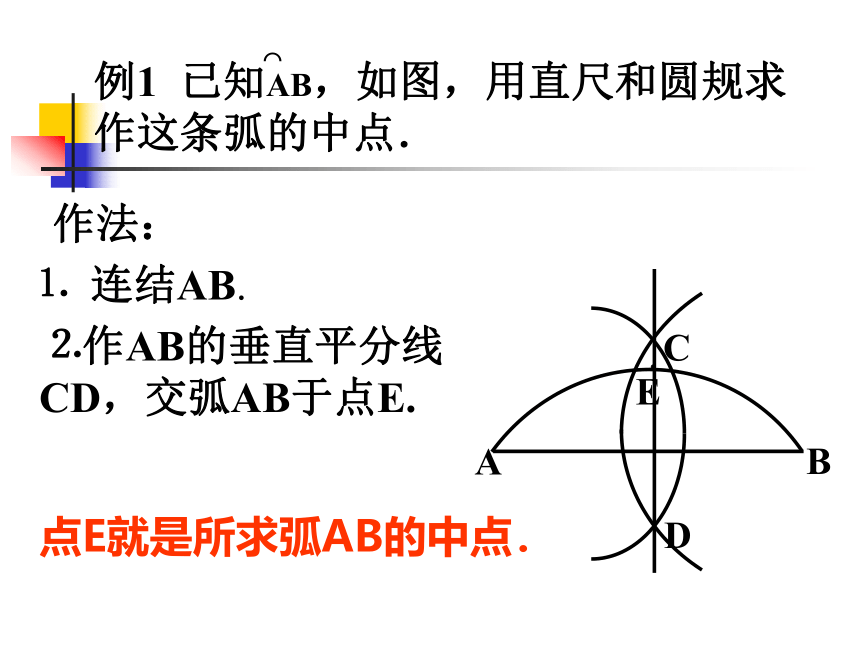
作法：
⒈
连结AB.
⒉作AB的垂直平分线
CD，交弧AB于点E.
点E就是所求弧AB的中点．
C
D
A
B
E
例1
已知AB，如图，用直尺和圆规求作这条弧的中点．
⌒
变式一：
求弧AB的四等分点．
C
D
A
B
E
F
G
m
n
变式一：
求弧AB的四等分点．
C
D
A
B
Ｍ
F
G
Ｔ
Ｅ
Ｎ
Ｈ
Ｐ
强调：等分弧时一定要作弧所对的弦的垂直平分线．
例2
已知：如图，线段AB与⊙O交于C、D两点，且OA=OB
．
求证：AC=BD
．
思路：
∴CM=DM
∵OA=OB
∴AM=BM
∴AC=BD．
．
O
A
B
C
M
D
作OM⊥AB，垂足为M
圆心到圆的一条弦的距离叫做弦心距．
小结：
1．画弦心距是圆中常见的辅助线；
．
O
A
B
C
r
d
2
．半径（r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路，它们之间的关系：
例3
如图，一条排水管的截面。已知排水管的半径OB=10，水面宽AB=16。求截面圆心O到水面的距离OC。
·
A
B
O
C
1．已知⊙0的半径为13，一条弦AB的弦心距
为5，则这条弦的弦长等于
．
24
2．如图，AB是⊙0的中直径，CD为弦，CD⊥AB于E，则下列结论中不一定成立的是（
）
A.CE=DE
B.
BC=BD
C．OE=BE
D．
∠COE=∠DOE
⌒
⌒
C
．
A
B
C
O
D
E
目标训练
．
O
A
B
C
r
d
3．过⊙O内一点M的最长弦长为10cm，
最短弦长为8cm，那么OM长为（
）
A．3
B．6cm
C．
cm
D．9cm
4．如图，⊙O的直径为10，弦AB长为8，M是弦AB上的动点，则OM的长的取值范围是（
）
A．3≤OM≤5
B．4≤OM≤5
C．3D．4．
A
B
O
M
A
A
6．已知⊙O的半径为10，弦AB∥CD，AB=12，CD=16，则AB和CD的距离为
．
2或14
5.如图，圆O的弦AB＝8
㎝
，
DC＝2㎝，
直径CE⊥AB于D，求半径OC的长为
5
r
r-2
4
１．本节课主要内容：（1）圆的轴对称性；（2）垂径定理．
2．垂径定理的应用：（1）作图；（2）计算和证明．
3．解题的主要方法：
总结回顾
（2）半径（r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路，它们之间的关系：
（1）画弦心距是圆中常见的辅助线；
1.
已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。
求证：AC＝BD。
E
.
A
C
D
B
O
课外拓展
2．如图，已知AB、AC为弦，OM⊥AB于点M，
ON⊥AC于点N
，BC=4，求MN的长．
??????????????