2020-2021学年八年级数学浙教版下册《第3章数据分析初步》期中复习优生辅导训练(word版含解析)
文档属性
| 名称 | 2020-2021学年八年级数学浙教版下册《第3章数据分析初步》期中复习优生辅导训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 127.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-19 18:25:29 | ||
图片预览




文档简介
2021年浙教版八年级数学下册《第3章数据分析初步》期中复习优生辅导训练(附答案)
1.某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如表,则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
锻炼时间/h
5
6
7
8
人数
6
15
10
4
A.6h,6h
B.6h,15h
C.6.5h,6h
D.6.5h,15h
2.八年级一班的平均年龄是12.5岁,方差是40,过一年后该班学生到九年级时,下列说法正确的是( )
A.平均年龄不变
B.年龄的方差不变
C.年龄的众数不变
D.年龄的中位数不变
3.下列说法正确的是( )
A.数据5,4,4,2,5的众数是4
B.数据0,1,2,5,﹣3的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣6,﹣3,4的中位数和平均数都是0
4.某小组有15人参加捐款,其中小明的捐款数比15人捐款的平均数多2元,下列说法正确的序号是( )
①小明的捐款数不可能最少;
②小明的捐款数可能最多;
③将捐款数按从少到多排列,小明的捐款数一定比中位数多;
④将捐款数按从少到多排列,小明的捐款数可能是众数.
A.①②④
B.②③④
C.①③④
D.①②③④
5.小明在计算一组数据的方差时,列出的公式如下:s2=,根据公式信息,下列说法中,错误的是( )
A.数据个数是5
B.数据平均数是8
C.数据众数是8
D.数据方差是0
6.某快递公司快递员张山某周投放快递物品件数为:有4天是30件,有2天是35件,有1天是41件,这周里张山日平均投递物品件数为( )
A.35.3件
B.35件
C.33件
D.30件
7.一组数据的方差为1.2,将这组数据扩大为原来的2倍,则所得新数据的方差为( )
A.1.2
B.2.4
C.1.44
D.4.8
8.一组数据为1,3,5,12,x,其中整数x是这组数据的中位数,则该组数据的平均数可能是( )
A.4
B.5
C.6
D.7
9.在防治新型冠状病毒的例行体温检查中,检测到5个人的体温分别是36.8℃、36.4℃、36.5℃、36.9℃、36.4℃,则数据36.8、36.4、36.5、36.9、36.4的众数是( )
A.36.8
B.36.5
C.36.4
D.36.9
10.一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,则数据x是( )
A.1
B.2
C.0或1
D.1或2
11.某地教育局拟招聘一批数学教师,现有一名应聘者笔试成绩88分、面试成绩90分,综合成绩按照笔试占45%、面试占55%进行计算,该应聘者的综合成绩为
分.
12.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为
.
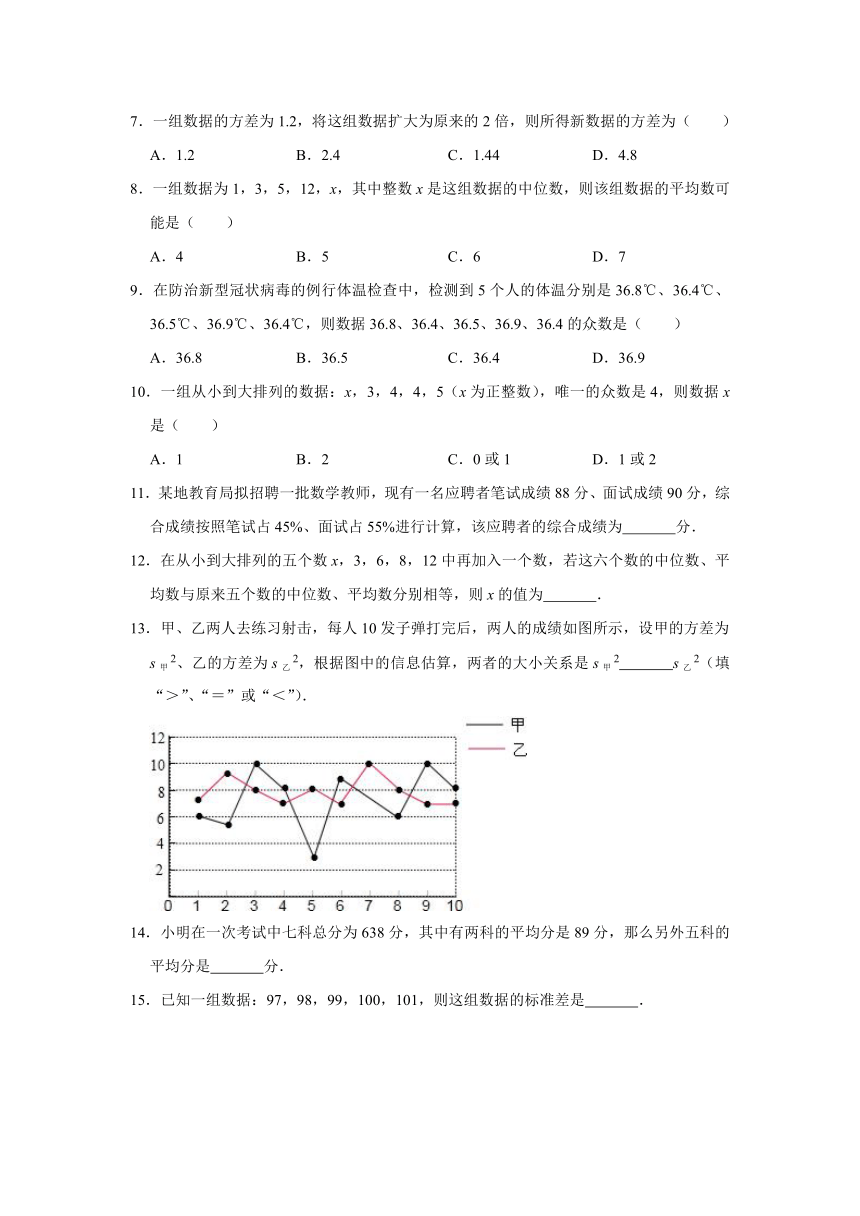
13.甲、乙两人去练习射击,每人10发子弹打完后,两人的成绩如图所示,设甲的方差为s甲2、乙的方差为s乙2,根据图中的信息估算,两者的大小关系是s甲2
s乙2(填“>”、“=”或“<”).
14.小明在一次考试中七科总分为638分,其中有两科的平均分是89分,那么另外五科的平均分是
分.
15.已知一组数据:97,98,99,100,101,则这组数据的标准差是
.
16.甲、乙两人各射击5次,成绩统计表如下:
环数(甲)
6
7
8
9
10
次数
1
1
1
1
1
环数(乙)
6
7
8
9
10
次数
0
2
2
0
1
那么射击成绩比较稳定的是
(填“甲”或“乙”).
17.一组数据5,x,8,2,3的平均数是4,则这组数据的中位数是
.
18.将一组数据中的每一个减去40后,所得新数据的平均数是2,则原来那组数据的平均数是
.
19.已知一组数据x1,x2,x3,…,xn的方差是7,那么数据x1﹣5,x2﹣5,x3﹣5,…,xn﹣5的方差为
.
20.若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x=
.
21.市体校射击队要从甲、乙两名射击队员中挑选一人参加省级比赛,因此,让他们在相同条件下各射击10次,成绩如图所示.
为分析成绩,教练根据统计图算出了甲队员成绩的平均数为8.5环、方差为1.05,请观察统计图,解答下列问题:
(1)先写出乙队员10次射击的成绩,再求10次射击成绩的平均数和方差;
(2)根据两人成绩分析的结果,若要选出总成绩高且发挥稳定的队员参加省级比赛,你认为选出的应是
,理由是:
.
22.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第1次
第2次
第3次
第4次
第5次
第6次
甲
10
9
8
8
10
9
乙
10
10
8
10
7
9
(1)根据表中的数据,分别计算甲、乙两人的平均成绩:=
环,=
环.
(2)分别计算甲、乙六次测试成绩的方差;S甲2=
环2,S乙2=
环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
23.某县教师进修学校初中研训部欲招聘一名打字员,对甲、乙两位候选人分别进行了工作态度、操作技能和学科知识的考核,他们的成绩如表所示(单位:分):
(1)若该初中研训部认为工作态度、操作技能和学科知识同等重要,则谁将被聘用?
候选人
工作态度
操作技能
学科知识
甲
83
79
81
乙
74
83
82
(2)若该初中研训部对于工作态度、操作技能、学科知识的成绩按照2:5:3的比确定,则谁将被聘用?
24.我市今年体育中考于5月18日开始,考试前,九(2)班的王茜和夏洁两位同学进行了8次50m短跑训练测试,她们的成绩分别如下:(单位:秒)
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
王茜
8.4
8.7
8.0
8.4
8.2
8.3
8.1
8.3
夏洁
8.7
8.3
8.6
7.9
8.0
8.4
8.2
8.3
(1)王茜和夏洁这8次训练的平均成绩分别是多少?
(2)按规定,女同学50m短跑达到8.3秒就可得到该项目满分15分,如果按她们目前的水平参加考试,你认为王茜和夏洁在该项目上谁得15分的可能性更大些?请说明理由.
25.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取5台进行测试,两种电子钟走时误差的数据如表(单位:秒):
编号类型
一
二
三
四
五
甲种电子钟
1
﹣3
﹣4
4
2
乙种电子钟
4
﹣3
﹣1
2
﹣2
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问你买哪种电子钟?为什么?
26.某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
李超:2.50,2.42,2.52,2.56,2.48,2.58
陈辉:2.54,2.48,2.50,2.48,2.54,2.52
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
参考答案
1.解:这组数据的中位数为第18个数据,即中位数为6h;6出现次数最多,众数为6h.
故选:A.
2.解:过一年后该班学生到九年级时,平均年龄是13.5岁,方差是40,
故选:B.
3.解:A、数据5,4,4,2,5中数据4和5出现的次数相同且最多,故众数为4和5,故本选项错误;
B、数据0,1,2,5,﹣3排序后为﹣3、0、1、2、5,故中位数为1,故本选项错误;
C、当一组数据的每个数据相等时,其众数及中位数相等,故本选项错误;
D、数据0、5、﹣6、﹣3、4的中位数为0,平均数为0,故本选项正确.
故选:D.
4.解:∵小明的捐款数比15人捐款的平均数多2元,
∴小明的捐款数不可能最少,故①正确;
小明的捐款数可能最多,故②正确;
将捐款数按从少到多排列,小明的捐款数不一定比第8名多,故③错误;
将捐款数按从少到多排列,小明的捐款数可能是众数,故④正确;
故选:A.
5.解:∵s2=,
∴样本容量是5,故选项A正确,
样本平均数是:=8,故选项B正确,
样本众数是8,故选项C正确,
样本方差是:s2=[(7﹣8)2+(8﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2]=,故选项D错误,
故选:D.
6.解:由题意可得,这周里张山日平均投递物品件数为:
==33(件).
故选:C.
7.解:根据方差的性质可知:
数据中的每个数据都扩大2倍,方差变为4s2,
则这组数据扩大为原来的2倍后方差为4×1.2=4.8.
故选:D.
8.解:∵数据1,3,5,12,x的中位数是整数x,
∴x=3或x=4或x=5,
当x=3时,这组数据的平均数为=4.8,
当x=4时,这组数据的平均数为=5,
当x=5时,这组数据的平均数为=5.2.
故选:B.
9.解:36.4出现的次数最多有2次,所以众数是36.4.
故选:C.
10.解:∵一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,
∴数据x是1或2.
故选:D.
11.解:88×45%+90×55%=39.6+49.5=89.1(分).
答:该应聘者的综合成绩为89.1分.
故答案为:89.1.
12.解:从小到大排列的五个数x,3,6,8,12的中位数是6,
∵再加入一个数,这六个数的中位数与原来五个数的中位数相等,
∴加入的一个数是6,
∵这六个数的平均数与原来五个数的平均数相等,
∴(x+3+6+8+12)=(x+3+6+6+8+12),
解得x=1.
故答案为:1.
13.解:从图看出:乙的成绩波动较小,说明它的成绩较稳定,方差较大.
故答案为:>.
14.解:(638﹣89×2)÷5
=(638﹣178)÷5
=460÷5
=92(分)
∴另外五科的平均分是92分.
故答案为:92.
15.解:=(97+98+99+100+101)=99,
s2=[(97﹣99)2+(98﹣99)2+(99﹣99)2+(100﹣99)2+(101﹣99)2]=2,
∴这组数据的标准差是,
故答案为:.
16.解:甲的平均数为:(6+7+8+9+10)=8,
甲的方差为:[(6﹣8)2+(7﹣8)2+(8﹣8)2+(9﹣8)2+(10﹣8)2]=2,
乙的平均数为:(7×2+8×2+10)=8,
乙的方差为:[(7﹣8)2+(7﹣8)2+(8﹣8)2+(8﹣8)2+(10﹣8)2]=1.2,
∵甲的方差>乙的方差,
∴射击成绩比较稳定的是乙.
故答案为:乙.
17.解:根据题意得,=4,解得x=2.
将这组数据从小到大的顺序排列:2,2,3,5,8.处于中间位置的那个数是3,由中位数的定义可知,这组数据的中位数是3.
故答案为:3.
18.解:由题意知,新的一组数据的平均数=[(x1﹣40)+(x2﹣40)+…+(xn﹣40)]=[(x1+x2+…+xn)﹣40n]=2.
∴(x1+x2+…+xn)﹣40=2.
∴(x1+x2+…+xn)=42,即原来的一组数据的平均数为42.
故答案为:42.
19.解:由题意知,原数据的平均数为,新数据的每一个数都减去了5,则平均数变为﹣5,
则原来的方差S12=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]=7,
现在的方差S22=[(x1﹣5﹣+5)2+(x2﹣5﹣+5)2+…+(xn﹣5﹣+5)2]
=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]=7,
所以方差不变.
故答案为:7.
20.解:∵一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,
∴这组数据可能是2,3,4,5,6或1,2,3,4,5,
∴x=1或6,
故答案为:1或6.
21.解;(1)乙队员10次射击的成绩分别为6,7,7,8,8,8,9,9,10,10;
乙10次射击成绩的平均数=(6+2×7+3×8+2×9+2×10)÷10=8.2,
方差=[(6﹣8.2)2+2×(7﹣8.2)2+3×(8﹣8.2)3+2×(9﹣8.2)2+2×(10﹣8.2)2]=1.56;
(2)∵8.5>8.2,S2甲>S2乙,
∴甲的平均数高,且成绩稳定,
∴选择甲同学参加射击比赛;
故答案为:甲;平均数高,且成绩稳定.
22.解:(1)=(10+9+8+8+10+9)=9,
=(10+10+8+10+7+9)=9,
故答案为:9;9;
(2)S甲2=[(10﹣9)2+(9﹣9)2+(8﹣9)2+(8﹣9)2+(10﹣9)2+(9﹣9)2]=,
S乙2=[(10﹣9)2+(10﹣9)2+(8﹣9)2+(10﹣9)2+(7﹣9)2+(9﹣9)2]=,
故答案为:;;
(3)甲参加省比赛更合适,因为甲比较稳定.
23.解:(1)=(83+79+81)÷3=243÷3=81(分),
=(74+83+82)÷3=239÷3≈79.7(分),
∵81>79.7,
∴甲将被聘用.
(2)=(83×2+79×5+81×3)÷(2+5+3)=804÷10=80.4(分),
=(74×2+83×5+82×3)÷(2+5+3)=809÷10=80.9(分),
∵80.9>80.4,
∴乙将被聘用.
24.解:(1)王茜的平均成绩:(8.4+8.7+8.0+8.4+8.2+8.3+8.1+8.3)=8.3,
夏洁的平均成绩:(8.7+8.3+8.6+7.9+8.0+8.4+8.2+8.3)=8.3;
(2)王茜得15分的可能性更大些,
王茜的方差:[(8.4﹣8.3)2+(8.7﹣8.3)2+(8.0﹣8.3)2+(8.4﹣8.3)2+(8.2﹣8.3)2+(8.3﹣8.3)2+(8.1﹣8.3)2+(8.4﹣8.3)2]=0.04,
夏洁的方差:[(8.7﹣8.3)2+(8.3﹣8.3)2+(8.6﹣8.3)2+(7.9﹣8.3)2+(8.0﹣8.3)2+(8.4﹣8.3)2+(8.2﹣8.3)2+(8.3﹣8.3)2]=0.065,
因为他们的平均数相同,王茜的方差小于夏洁的方差,
所以王茜的成绩比较稳定,
所以王茜得15分的可能性更大些.
25.解:(1)甲种电子钟走时误差的平均数是(1﹣3﹣4+4+2)=0,
乙种电子钟走时误差的平均数是:(4﹣3﹣1+2﹣2)=0.
(2)S2甲=[(1﹣0)2+(﹣3﹣0)2+…+(2﹣0)2]=×46=9.2(s2),
S2乙=[(4﹣0)2+(﹣3﹣0)2+…+(﹣2﹣0)2]=×34=6.8(s2),
故甲乙两种电子钟走时误差的方差分别是9.2s2和6.8s2;
(3)因为乙的方差小于甲的方差,所以乙更稳定,故买乙种电子钟.
26.解:(1)分别计算李超和陈辉两人的跳高平均成绩:
李超的平均成绩为:(2.50+2.42+2.52+2.56+2.48+2.58)=2.51m,
陈辉的平均成绩为:(2.54+2.48+2.50+2.48+2.54+2.52)=2.51m;
(2)分别计算李超和陈辉两人的跳高成绩的方差分别:
S李超2=[(2.50﹣2.51)2+(2.42﹣2.51)2+(2.52﹣2.51)2+(2.56﹣2.51)2+(2.48﹣2.51)2+(2.58﹣2.51)2]=0.00277,
S陈辉2=[(2.54﹣2.51)2+(2.48﹣2.51)2+(2.50﹣2.51)2+(2.48﹣2.51)2+(2.54﹣2.51)2+(2.52﹣2.51)2]=0.00633,
∴李超运动员的成绩更为稳定;
(3)若跳过2.55m就很可能获得冠军,则在6次成绩中,李超2次都跳过了2.55m,而陈辉一次没有,所以应选李超运动员参加;
1.某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如表,则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
锻炼时间/h
5
6
7
8
人数
6
15
10
4
A.6h,6h
B.6h,15h
C.6.5h,6h
D.6.5h,15h
2.八年级一班的平均年龄是12.5岁,方差是40,过一年后该班学生到九年级时,下列说法正确的是( )
A.平均年龄不变
B.年龄的方差不变
C.年龄的众数不变
D.年龄的中位数不变
3.下列说法正确的是( )
A.数据5,4,4,2,5的众数是4
B.数据0,1,2,5,﹣3的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣6,﹣3,4的中位数和平均数都是0
4.某小组有15人参加捐款,其中小明的捐款数比15人捐款的平均数多2元,下列说法正确的序号是( )
①小明的捐款数不可能最少;
②小明的捐款数可能最多;
③将捐款数按从少到多排列,小明的捐款数一定比中位数多;
④将捐款数按从少到多排列,小明的捐款数可能是众数.
A.①②④
B.②③④
C.①③④
D.①②③④
5.小明在计算一组数据的方差时,列出的公式如下:s2=,根据公式信息,下列说法中,错误的是( )
A.数据个数是5
B.数据平均数是8
C.数据众数是8
D.数据方差是0
6.某快递公司快递员张山某周投放快递物品件数为:有4天是30件,有2天是35件,有1天是41件,这周里张山日平均投递物品件数为( )
A.35.3件
B.35件
C.33件
D.30件
7.一组数据的方差为1.2,将这组数据扩大为原来的2倍,则所得新数据的方差为( )
A.1.2
B.2.4
C.1.44
D.4.8
8.一组数据为1,3,5,12,x,其中整数x是这组数据的中位数,则该组数据的平均数可能是( )
A.4
B.5
C.6
D.7
9.在防治新型冠状病毒的例行体温检查中,检测到5个人的体温分别是36.8℃、36.4℃、36.5℃、36.9℃、36.4℃,则数据36.8、36.4、36.5、36.9、36.4的众数是( )
A.36.8
B.36.5
C.36.4
D.36.9
10.一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,则数据x是( )
A.1
B.2
C.0或1
D.1或2
11.某地教育局拟招聘一批数学教师,现有一名应聘者笔试成绩88分、面试成绩90分,综合成绩按照笔试占45%、面试占55%进行计算,该应聘者的综合成绩为
分.
12.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为
.
13.甲、乙两人去练习射击,每人10发子弹打完后,两人的成绩如图所示,设甲的方差为s甲2、乙的方差为s乙2,根据图中的信息估算,两者的大小关系是s甲2
s乙2(填“>”、“=”或“<”).
14.小明在一次考试中七科总分为638分,其中有两科的平均分是89分,那么另外五科的平均分是
分.
15.已知一组数据:97,98,99,100,101,则这组数据的标准差是
.
16.甲、乙两人各射击5次,成绩统计表如下:
环数(甲)
6
7
8
9
10
次数
1
1
1
1
1
环数(乙)
6
7
8
9
10
次数
0
2
2
0
1
那么射击成绩比较稳定的是
(填“甲”或“乙”).
17.一组数据5,x,8,2,3的平均数是4,则这组数据的中位数是
.
18.将一组数据中的每一个减去40后,所得新数据的平均数是2,则原来那组数据的平均数是
.
19.已知一组数据x1,x2,x3,…,xn的方差是7,那么数据x1﹣5,x2﹣5,x3﹣5,…,xn﹣5的方差为
.
20.若一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,则x=
.
21.市体校射击队要从甲、乙两名射击队员中挑选一人参加省级比赛,因此,让他们在相同条件下各射击10次,成绩如图所示.
为分析成绩,教练根据统计图算出了甲队员成绩的平均数为8.5环、方差为1.05,请观察统计图,解答下列问题:
(1)先写出乙队员10次射击的成绩,再求10次射击成绩的平均数和方差;
(2)根据两人成绩分析的结果,若要选出总成绩高且发挥稳定的队员参加省级比赛,你认为选出的应是
,理由是:
.
22.市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第1次
第2次
第3次
第4次
第5次
第6次
甲
10
9
8
8
10
9
乙
10
10
8
10
7
9
(1)根据表中的数据,分别计算甲、乙两人的平均成绩:=
环,=
环.
(2)分别计算甲、乙六次测试成绩的方差;S甲2=
环2,S乙2=
环2.
(3)根据(1)、(2)计算的结果,你认为推荐谁参加省比赛更合适,请说明理由.
23.某县教师进修学校初中研训部欲招聘一名打字员,对甲、乙两位候选人分别进行了工作态度、操作技能和学科知识的考核,他们的成绩如表所示(单位:分):
(1)若该初中研训部认为工作态度、操作技能和学科知识同等重要,则谁将被聘用?
候选人
工作态度
操作技能
学科知识
甲
83
79
81
乙
74
83
82
(2)若该初中研训部对于工作态度、操作技能、学科知识的成绩按照2:5:3的比确定,则谁将被聘用?
24.我市今年体育中考于5月18日开始,考试前,九(2)班的王茜和夏洁两位同学进行了8次50m短跑训练测试,她们的成绩分别如下:(单位:秒)
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
王茜
8.4
8.7
8.0
8.4
8.2
8.3
8.1
8.3
夏洁
8.7
8.3
8.6
7.9
8.0
8.4
8.2
8.3
(1)王茜和夏洁这8次训练的平均成绩分别是多少?
(2)按规定,女同学50m短跑达到8.3秒就可得到该项目满分15分,如果按她们目前的水平参加考试,你认为王茜和夏洁在该项目上谁得15分的可能性更大些?请说明理由.
25.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取5台进行测试,两种电子钟走时误差的数据如表(单位:秒):
编号类型
一
二
三
四
五
甲种电子钟
1
﹣3
﹣4
4
2
乙种电子钟
4
﹣3
﹣1
2
﹣2
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问你买哪种电子钟?为什么?
26.某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
李超:2.50,2.42,2.52,2.56,2.48,2.58
陈辉:2.54,2.48,2.50,2.48,2.54,2.52
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
参考答案
1.解:这组数据的中位数为第18个数据,即中位数为6h;6出现次数最多,众数为6h.
故选:A.
2.解:过一年后该班学生到九年级时,平均年龄是13.5岁,方差是40,
故选:B.
3.解:A、数据5,4,4,2,5中数据4和5出现的次数相同且最多,故众数为4和5,故本选项错误;
B、数据0,1,2,5,﹣3排序后为﹣3、0、1、2、5,故中位数为1,故本选项错误;
C、当一组数据的每个数据相等时,其众数及中位数相等,故本选项错误;
D、数据0、5、﹣6、﹣3、4的中位数为0,平均数为0,故本选项正确.
故选:D.
4.解:∵小明的捐款数比15人捐款的平均数多2元,
∴小明的捐款数不可能最少,故①正确;
小明的捐款数可能最多,故②正确;
将捐款数按从少到多排列,小明的捐款数不一定比第8名多,故③错误;
将捐款数按从少到多排列,小明的捐款数可能是众数,故④正确;
故选:A.
5.解:∵s2=,
∴样本容量是5,故选项A正确,
样本平均数是:=8,故选项B正确,
样本众数是8,故选项C正确,
样本方差是:s2=[(7﹣8)2+(8﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2]=,故选项D错误,
故选:D.
6.解:由题意可得,这周里张山日平均投递物品件数为:
==33(件).
故选:C.
7.解:根据方差的性质可知:
数据中的每个数据都扩大2倍,方差变为4s2,
则这组数据扩大为原来的2倍后方差为4×1.2=4.8.
故选:D.
8.解:∵数据1,3,5,12,x的中位数是整数x,
∴x=3或x=4或x=5,
当x=3时,这组数据的平均数为=4.8,
当x=4时,这组数据的平均数为=5,
当x=5时,这组数据的平均数为=5.2.
故选:B.
9.解:36.4出现的次数最多有2次,所以众数是36.4.
故选:C.
10.解:∵一组从小到大排列的数据:x,3,4,4,5(x为正整数),唯一的众数是4,
∴数据x是1或2.
故选:D.
11.解:88×45%+90×55%=39.6+49.5=89.1(分).
答:该应聘者的综合成绩为89.1分.
故答案为:89.1.
12.解:从小到大排列的五个数x,3,6,8,12的中位数是6,
∵再加入一个数,这六个数的中位数与原来五个数的中位数相等,
∴加入的一个数是6,
∵这六个数的平均数与原来五个数的平均数相等,
∴(x+3+6+8+12)=(x+3+6+6+8+12),
解得x=1.
故答案为:1.
13.解:从图看出:乙的成绩波动较小,说明它的成绩较稳定,方差较大.
故答案为:>.
14.解:(638﹣89×2)÷5
=(638﹣178)÷5
=460÷5
=92(分)
∴另外五科的平均分是92分.
故答案为:92.
15.解:=(97+98+99+100+101)=99,
s2=[(97﹣99)2+(98﹣99)2+(99﹣99)2+(100﹣99)2+(101﹣99)2]=2,
∴这组数据的标准差是,
故答案为:.
16.解:甲的平均数为:(6+7+8+9+10)=8,
甲的方差为:[(6﹣8)2+(7﹣8)2+(8﹣8)2+(9﹣8)2+(10﹣8)2]=2,
乙的平均数为:(7×2+8×2+10)=8,
乙的方差为:[(7﹣8)2+(7﹣8)2+(8﹣8)2+(8﹣8)2+(10﹣8)2]=1.2,
∵甲的方差>乙的方差,
∴射击成绩比较稳定的是乙.
故答案为:乙.
17.解:根据题意得,=4,解得x=2.
将这组数据从小到大的顺序排列:2,2,3,5,8.处于中间位置的那个数是3,由中位数的定义可知,这组数据的中位数是3.
故答案为:3.
18.解:由题意知,新的一组数据的平均数=[(x1﹣40)+(x2﹣40)+…+(xn﹣40)]=[(x1+x2+…+xn)﹣40n]=2.
∴(x1+x2+…+xn)﹣40=2.
∴(x1+x2+…+xn)=42,即原来的一组数据的平均数为42.
故答案为:42.
19.解:由题意知,原数据的平均数为,新数据的每一个数都减去了5,则平均数变为﹣5,
则原来的方差S12=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]=7,
现在的方差S22=[(x1﹣5﹣+5)2+(x2﹣5﹣+5)2+…+(xn﹣5﹣+5)2]
=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]=7,
所以方差不变.
故答案为:7.
20.解:∵一组数据2,3,4,5,x的方差与另一组数据5,6,7,8,9的方差相等,
∴这组数据可能是2,3,4,5,6或1,2,3,4,5,
∴x=1或6,
故答案为:1或6.
21.解;(1)乙队员10次射击的成绩分别为6,7,7,8,8,8,9,9,10,10;
乙10次射击成绩的平均数=(6+2×7+3×8+2×9+2×10)÷10=8.2,
方差=[(6﹣8.2)2+2×(7﹣8.2)2+3×(8﹣8.2)3+2×(9﹣8.2)2+2×(10﹣8.2)2]=1.56;
(2)∵8.5>8.2,S2甲>S2乙,
∴甲的平均数高,且成绩稳定,
∴选择甲同学参加射击比赛;
故答案为:甲;平均数高,且成绩稳定.
22.解:(1)=(10+9+8+8+10+9)=9,
=(10+10+8+10+7+9)=9,
故答案为:9;9;
(2)S甲2=[(10﹣9)2+(9﹣9)2+(8﹣9)2+(8﹣9)2+(10﹣9)2+(9﹣9)2]=,
S乙2=[(10﹣9)2+(10﹣9)2+(8﹣9)2+(10﹣9)2+(7﹣9)2+(9﹣9)2]=,
故答案为:;;
(3)甲参加省比赛更合适,因为甲比较稳定.
23.解:(1)=(83+79+81)÷3=243÷3=81(分),
=(74+83+82)÷3=239÷3≈79.7(分),
∵81>79.7,
∴甲将被聘用.
(2)=(83×2+79×5+81×3)÷(2+5+3)=804÷10=80.4(分),
=(74×2+83×5+82×3)÷(2+5+3)=809÷10=80.9(分),
∵80.9>80.4,
∴乙将被聘用.
24.解:(1)王茜的平均成绩:(8.4+8.7+8.0+8.4+8.2+8.3+8.1+8.3)=8.3,
夏洁的平均成绩:(8.7+8.3+8.6+7.9+8.0+8.4+8.2+8.3)=8.3;
(2)王茜得15分的可能性更大些,
王茜的方差:[(8.4﹣8.3)2+(8.7﹣8.3)2+(8.0﹣8.3)2+(8.4﹣8.3)2+(8.2﹣8.3)2+(8.3﹣8.3)2+(8.1﹣8.3)2+(8.4﹣8.3)2]=0.04,
夏洁的方差:[(8.7﹣8.3)2+(8.3﹣8.3)2+(8.6﹣8.3)2+(7.9﹣8.3)2+(8.0﹣8.3)2+(8.4﹣8.3)2+(8.2﹣8.3)2+(8.3﹣8.3)2]=0.065,
因为他们的平均数相同,王茜的方差小于夏洁的方差,
所以王茜的成绩比较稳定,
所以王茜得15分的可能性更大些.
25.解:(1)甲种电子钟走时误差的平均数是(1﹣3﹣4+4+2)=0,
乙种电子钟走时误差的平均数是:(4﹣3﹣1+2﹣2)=0.
(2)S2甲=[(1﹣0)2+(﹣3﹣0)2+…+(2﹣0)2]=×46=9.2(s2),
S2乙=[(4﹣0)2+(﹣3﹣0)2+…+(﹣2﹣0)2]=×34=6.8(s2),
故甲乙两种电子钟走时误差的方差分别是9.2s2和6.8s2;
(3)因为乙的方差小于甲的方差,所以乙更稳定,故买乙种电子钟.
26.解:(1)分别计算李超和陈辉两人的跳高平均成绩:
李超的平均成绩为:(2.50+2.42+2.52+2.56+2.48+2.58)=2.51m,
陈辉的平均成绩为:(2.54+2.48+2.50+2.48+2.54+2.52)=2.51m;
(2)分别计算李超和陈辉两人的跳高成绩的方差分别:
S李超2=[(2.50﹣2.51)2+(2.42﹣2.51)2+(2.52﹣2.51)2+(2.56﹣2.51)2+(2.48﹣2.51)2+(2.58﹣2.51)2]=0.00277,
S陈辉2=[(2.54﹣2.51)2+(2.48﹣2.51)2+(2.50﹣2.51)2+(2.48﹣2.51)2+(2.54﹣2.51)2+(2.52﹣2.51)2]=0.00633,
∴李超运动员的成绩更为稳定;
(3)若跳过2.55m就很可能获得冠军,则在6次成绩中,李超2次都跳过了2.55m,而陈辉一次没有,所以应选李超运动员参加;
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
