4.2.2 平行线间的线段同步练习(含解析)
文档属性
| 名称 | 4.2.2 平行线间的线段同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 08:16:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级下册4.2.2平行线间的线段
同步练习
一、单选题
1.如图所示,
∥
,则平行线
与
间的距离是(???
)
A.?线段AB的长度????????????????B.?线段BC的长度????????????????C.?线段CD的长度????????????????D.?线段DE的长度
2.平行线之间的距离是指(???)
A.?从一条直线上一点到另一条直线的垂线段;
B.?从一条直线上一点到另一条直线的垂线段长度;
C.?从一条直线上一点到另一条直线的垂线的长度;
D.?从一条直线上一点到另一条直线上的一点间线段的长度.
3.如图,直线l1∥l2
,
线段AB的端点A,B分别在直线11和12上,AB=6.点C在直线12上,∠ABC=30°,则这两条直线的距离是(??
)
A.?3????????????????????????????????????????B.?6????????????????????????????????????????C.?2
????????????????????????????????????????D.?3
4.如图,直线
,点P是直线
上一个动点,当点P的位置发生变化时,三角形
的面积(?
)
A.?向左移动变小???????????????????????B.?向右移动变小???????????????????????C.?始终不变???????????????????????D.?无法确定
5.把线段
沿水平方向平移
,平移后为线段
,则线段
与线段
之间的距离是(???
).
A.?等于
???????????????????B.?小于
???????????????????C.?小于或等于
???????????????????D.?大于或等于
6.如图,一绿地的两边AD,BC平行,绿地中间开辟两条道路,而每条道路的宽处处相等,且EF=GH=PQ=MN,则两条道路的占地面积情况是(??
)
A.?不相等?????????????????B.?四边形GHNM面积要大?????????????????C.?四边形EFQP的面积大?????????????????D.?相等
7.如图,AB∥DC,ED∥BC,AE∥BD,那么图中和△ABD面积相等的三角形(不包括△ABD)有(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
8.直线a上有一点A,直线b上有一点B,且a∥b.点P在直线a,b之间,若PA=3,PB=4,则直线a、b之间的距离(??
)
A.?等于7????????????????????????????????B.?小于7????????????????????????????????C.?不小于7????????????????????????????????D.?不大于7
9.如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD=10cm2
,
S△ACD为(?
)
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?7
10.如图
,若
表示三角形
的面积,
表示三角形
的面积,则下列结论正确的是(
?)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
二、填空题
11.两条平行线间的所有________线段都相等.
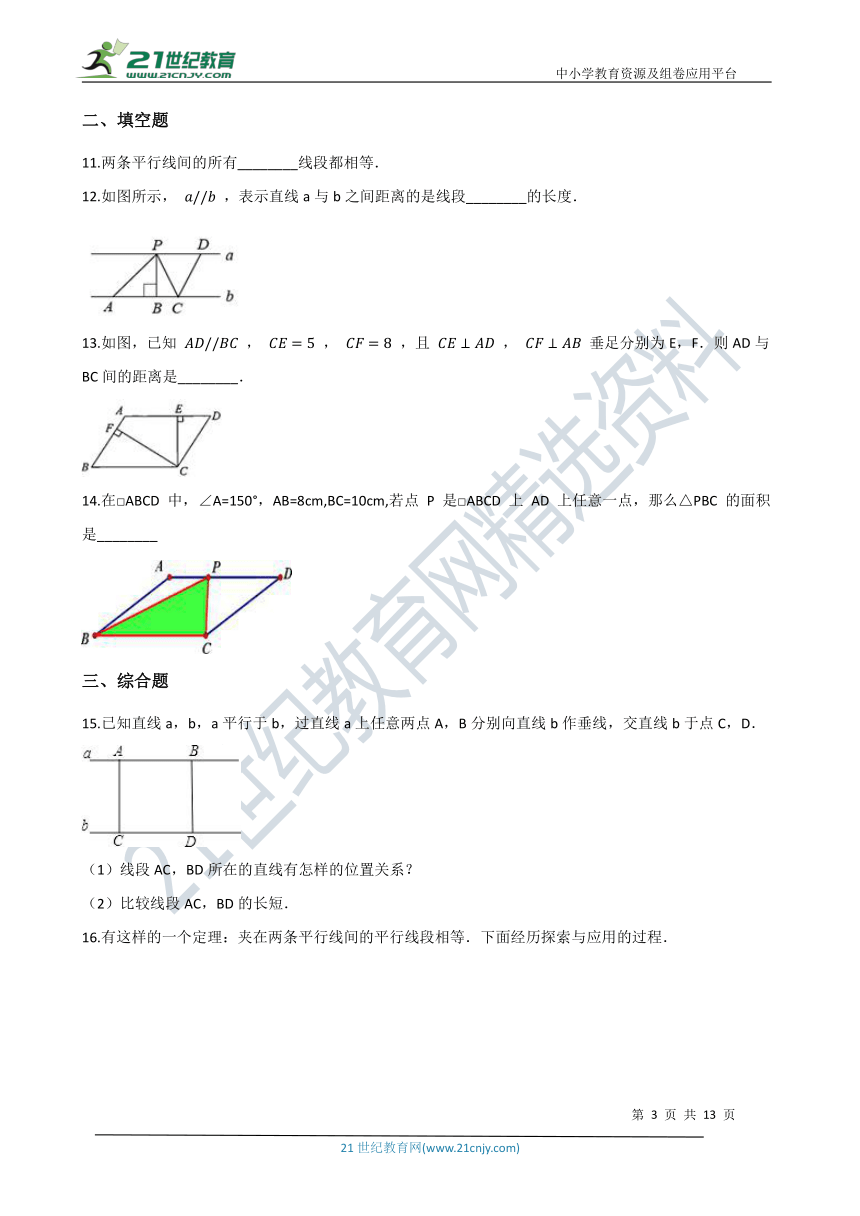
12.如图所示,
,表示直线a与b之间距离的是线段________的长度.
13.如图,已知
,
,
,且
,
垂足分别为E,F.则AD与BC间的距离是________.
14.在□ABCD
中,∠A=150°,AB=8cm,BC=10cm,若点
P
是□ABCD
上
AD
上任意一点,那么△PBC
的面积是________
三、综合题
15.已知直线a,b,a平行于b,过直线a上任意两点A,B分别向直线b作垂线,交直线b于点C,D.
(1)线段AC,BD所在的直线有怎样的位置关系?
(2)比较线段AC,BD的长短.
16.有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
(1)探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
(2)应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
(3)应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
17.如图,在△ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以2cm/s的速度运动,当点E先出发1s后,点F也从点B出发沿射线BC以
cm/s的速度运动,分别连结AF,CE.设点F运动时间为t(s),其中t>0.
(1)当t为何值时,∠BAF<∠BAC;
(2)当t为何值时,AE=CF;
(3)当t为何值时,S△ABF+S△ACE<S△ABC
.
答案解析部分
一、单选题
1.
B
考点:平行线之间的距离
解:∵CB⊥
于点B,
∴
与
两平行线间的距离就是线段BC的长度,故B选项符合题意;
∵线段AB、线段CD、线段DE都不是
与
之间的垂线段,A、C、D都不符合题意;
故答案为:B.
分析:根据平行线之间距离的定义对各选项进行逐一分析即可.
2.
B
考点:平行线之间的距离
分析:根据平行线间的距离的定义直接进行选择即可。
解:平行线之间的距离是指:从一条直线上一点到另一条直线的垂线段长度.
故选B.
解答本题的关键是熟练掌握平行线之间的距离是指:从一条直线上一点到另一条直线的垂线段长度。
3.
A
考点:平行线之间的距离,含30°角的直角三角形
解:如图,过点A作AH⊥BC于H.
在Rt△ABH中,∵∠AHB=90°,AB=6,∠ABH=30°,
∴AH=
AB=3,
故答案为:A.
分析:如图,过点A作AH⊥BC于H.解直角三角形求出AH即可.
4.
C
考点:平行线之间的距离
解:∵直线
,点P是直线
AB
上一个动点,
∴无论点P怎么移动,点P到CD的距离不变,
∴三角形PCD?
的底不变,高不变,面积也不变,
故答案为:C.
分析:根据平行线间的距离处处相等,可知三角形
PCD
的底不变,高相等,从而得出面积始终不变.
5.
C
考点:平行线之间的距离
解:如图(1),若线段AB与水平方向垂直,此时线段
与线段
之间的距离是5cm;
如图(2),若线段AB与水平方向不垂直,此时线段
与线段
之间的距离小于5cm;
故答案为:C.
分析:分两种情况:如图(1),线段AB与水平方向垂直;如图(2),线段AB与水平方向不垂直,分别进行讨论即可得出答案.
6.D
考点:平行线之间的距离
解:设EF=GH=PQ=MN=x,
由面积公式得:两条道路的占地面积分别是AB?x和AB?x,
即两条道路的占地面积情况是相等,
故选D.
分析:根据平行线之间的距离和面积公式求出即可.
7.B
考点:平行线之间的距离
解:∵AB∥DC,
∴△ABC与△ABD的面积相等,
∵AE∥BD,
∴△BED与△ABD的面积相等,
∵ED∥BC找不到与△ABD等底等高的三角形,
∴和△ABD的面积相等的三角形有△ABC、△BDE,共2个.
故选B.
分析:根据两平行直线之间的距离相等,再根据等底等高的三角形的面积相等,找出与△ABD等底等高的三角形即可.
8.
D
考点:平行线之间的距离
解:如图,
当点A、B、P共线,且AB⊥a时,直线a、b之间的最短,所以直线a、b之间的距离≤PA+PB=3+4=7.
即直线a、b之间的距离不大于7.
故选:D.
分析:当点A、B、P共线,且AB⊥a时,直线a、b之间的距离为PA+PB.
9.
A
考点:平行线之间的距离
解:∵四边形ABCD中,AD∥BC,AC与BD相交于点O,S△ABD=10cm2
,
∴△ABD和△ACD如果都以AD做底边时,此时底边上的高相等,
∴S△ACD=10cm2
,
故选A.
分析:根据题意可知△ABD和△ACD如果都以AD做底边时,此时底边上的高相等,从而可以得到S△ACD的值.
10.
A
考点:平行线之间的距离,三角形的面积
解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示
由题意得:
,
∵AD∥BC
∴AE=DF
∴S1=S2
故答案为:A.
分析:本题不难发现两个三角形的底都是BC,要比较两个三角形的面积,就是比较高的大小,把两个三角形的高画出来,再根据平行,即可得到高相等,所以两个三角形的面积相等.
二、填空题
11.公垂
考点:平行线之间的距离
解:两条平行线间的所有公垂线段都相等,
故答案为:公垂.
分析:根据“在两条平行线之间的线段中,垂直两条平行线的线段最短,这条线段的长叫做平行线之间的距离”可知:在两条平行线之间再画几条和平行线垂直的线段,这些线段的长度都相等;据此判断即可.
12.
BP
考点:平行线之间的距离
解:由图可得,a∥b,BP⊥a,
∴直线a与直线b之间的距离是线段BP的长度,
故答案为:BP.
分析:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,由此可得出答案.
13.
5
考点:平行线之间的距离
解:AD与BC间的距离就是CE的长度,
?
∴AD与BC间的距离是5,
故答案为:5.
分析:AD与BC间的距离就是CE的长度,从而可得出答案.
14.
考点:平行线之间的距离,三角形的面积
解:作AE⊥BC于E,
∵四边形ABCD是平行四边形,且∠BAD=150
,
∴∠ABC=180
150
=30
,
在Rt△ABE中,AB=8cm,∠AEB=90
,∠ABC=30
,
∴AE=
AB=4cm,
∵
(
)
.
故答案为:
20
.
分析:根据平行线之间的距离处处相等,求出BC和AE的长,再利用三角形的面积计算公式求解即可。
三、综合题
15.
(1)解:∵AC⊥a,BD⊥a,
∴AC∥BD
(2)解:∵a∥b,AC⊥a,BD⊥a,
∴AC=BD
考点:平行线之间的距离
分析:(1)根据平行线的判定定理即可得出结论;(2)根据平行线间的距离即可得出结论.
16.
(1)证明:如图1,
连接AC,
∵AD∥BC,∴∠DAC=∠BCA
∵AB∥CD.∴∠BAC=∠DCA
在△ABC和△CDA中,
,
∴△ABC≌△CDA(ASA),
∴AB=CD
(2)证明:如图2,
作DE∥AB交BC于点E,
∵AD∥BC,
∴AB=DE
∵AB=CD,
∴DE=CD,
∴∠DEC=∠C
∵DE∥AB,
∴∠B=∠DEC,
∴∠B=∠C
(3)解:如图3,
作DF∥AC交BC的延长线于点F
∵AD∥BC,∴AC=DF、AD=CF,
∵DF∥AC,∴∠BDF=∠BEC,
∵AC⊥BD,∴∠BDF=∠BEC=90°,
在Rt△BDF中,由勾股定理得:BF=5,
故BC+AD=BC+CF=BF=5.
考点:平行线之间的距离,全等三角形的判定与性质
分析:探索:利用平行线的性质得出,∠DAC=∠BCA,∠BAC=∠DCA,进而得出△ABC≌△CDA(ASA),求出即可;应用一:作DE∥AB交BC于点E,利用平行线的性质得出∠B=∠C;应用二:利用平行线的性质结合勾股定理得出AD与BC两条线段的和.
17.
(1)解:当BF<BC时,∠BAF<∠BAC,
∴
<6,
解得t<
,
当0<t<
时,∠BAF<∠BAC
(2)解:分两种情况讨论:
????
点F在点C左侧时,AE=CF,
则2(t+1)=6﹣
t,
解得t=
;
②当点F在点C的右侧时,AE=CF,
则2(t+1)=
t﹣6,
解得t=
,
综上所述,t=
,t=
时,AE=CF
(3)解:当BF+AE<BC,S△ABF+S△ACE<S△ABC
,
t+2(t+1)<6,
解得t<
,
当0<t<
时,S△ABF+S△ACE<S△ABC
考点:平行线之间的距离,三角形的面积
分析:(1)根据边越长,边所对的角越大,可得答案;(2)分类讨论:当点F在点C左侧时,点F再点C的右侧时,可得关于t的一元一次方程,根据解方程,可得答案;(3)根据平行线间的距离相等,可得三角形的高相等,根据等高的三角形的底边越长,三角形的面积越大,可得不等式.
21世纪教育网(www.21cnjy.com)
初中数学浙教版八年级下册4.2.2平行线间的线段
同步练习
一、单选题
1.如图所示,
∥
,则平行线
与
间的距离是(???
)
A.?线段AB的长度????????????????B.?线段BC的长度????????????????C.?线段CD的长度????????????????D.?线段DE的长度
2.平行线之间的距离是指(???)
A.?从一条直线上一点到另一条直线的垂线段;
B.?从一条直线上一点到另一条直线的垂线段长度;
C.?从一条直线上一点到另一条直线的垂线的长度;
D.?从一条直线上一点到另一条直线上的一点间线段的长度.
3.如图,直线l1∥l2
,
线段AB的端点A,B分别在直线11和12上,AB=6.点C在直线12上,∠ABC=30°,则这两条直线的距离是(??
)
A.?3????????????????????????????????????????B.?6????????????????????????????????????????C.?2
????????????????????????????????????????D.?3
4.如图,直线
,点P是直线
上一个动点,当点P的位置发生变化时,三角形
的面积(?
)
A.?向左移动变小???????????????????????B.?向右移动变小???????????????????????C.?始终不变???????????????????????D.?无法确定
5.把线段
沿水平方向平移
,平移后为线段
,则线段
与线段
之间的距离是(???
).
A.?等于
???????????????????B.?小于
???????????????????C.?小于或等于
???????????????????D.?大于或等于
6.如图,一绿地的两边AD,BC平行,绿地中间开辟两条道路,而每条道路的宽处处相等,且EF=GH=PQ=MN,则两条道路的占地面积情况是(??
)
A.?不相等?????????????????B.?四边形GHNM面积要大?????????????????C.?四边形EFQP的面积大?????????????????D.?相等
7.如图,AB∥DC,ED∥BC,AE∥BD,那么图中和△ABD面积相等的三角形(不包括△ABD)有(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
8.直线a上有一点A,直线b上有一点B,且a∥b.点P在直线a,b之间,若PA=3,PB=4,则直线a、b之间的距离(??
)
A.?等于7????????????????????????????????B.?小于7????????????????????????????????C.?不小于7????????????????????????????????D.?不大于7
9.如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,若S△ABD=10cm2
,
S△ACD为(?
)
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?7
10.如图
,若
表示三角形
的面积,
表示三角形
的面积,则下列结论正确的是(
?)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
二、填空题
11.两条平行线间的所有________线段都相等.
12.如图所示,
,表示直线a与b之间距离的是线段________的长度.
13.如图,已知
,
,
,且
,
垂足分别为E,F.则AD与BC间的距离是________.
14.在□ABCD
中,∠A=150°,AB=8cm,BC=10cm,若点
P
是□ABCD
上
AD
上任意一点,那么△PBC
的面积是________
三、综合题
15.已知直线a,b,a平行于b,过直线a上任意两点A,B分别向直线b作垂线,交直线b于点C,D.
(1)线段AC,BD所在的直线有怎样的位置关系?
(2)比较线段AC,BD的长短.
16.有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
(1)探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
(2)应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;
(3)应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.
17.如图,在△ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以2cm/s的速度运动,当点E先出发1s后,点F也从点B出发沿射线BC以
cm/s的速度运动,分别连结AF,CE.设点F运动时间为t(s),其中t>0.
(1)当t为何值时,∠BAF<∠BAC;
(2)当t为何值时,AE=CF;
(3)当t为何值时,S△ABF+S△ACE<S△ABC
.
答案解析部分
一、单选题
1.
B
考点:平行线之间的距离
解:∵CB⊥
于点B,
∴
与
两平行线间的距离就是线段BC的长度,故B选项符合题意;
∵线段AB、线段CD、线段DE都不是
与
之间的垂线段,A、C、D都不符合题意;
故答案为:B.
分析:根据平行线之间距离的定义对各选项进行逐一分析即可.
2.
B
考点:平行线之间的距离
分析:根据平行线间的距离的定义直接进行选择即可。
解:平行线之间的距离是指:从一条直线上一点到另一条直线的垂线段长度.
故选B.
解答本题的关键是熟练掌握平行线之间的距离是指:从一条直线上一点到另一条直线的垂线段长度。
3.
A
考点:平行线之间的距离,含30°角的直角三角形
解:如图,过点A作AH⊥BC于H.
在Rt△ABH中,∵∠AHB=90°,AB=6,∠ABH=30°,
∴AH=
AB=3,
故答案为:A.
分析:如图,过点A作AH⊥BC于H.解直角三角形求出AH即可.
4.
C
考点:平行线之间的距离
解:∵直线
,点P是直线
AB
上一个动点,
∴无论点P怎么移动,点P到CD的距离不变,
∴三角形PCD?
的底不变,高不变,面积也不变,
故答案为:C.
分析:根据平行线间的距离处处相等,可知三角形
PCD
的底不变,高相等,从而得出面积始终不变.
5.
C
考点:平行线之间的距离
解:如图(1),若线段AB与水平方向垂直,此时线段
与线段
之间的距离是5cm;
如图(2),若线段AB与水平方向不垂直,此时线段
与线段
之间的距离小于5cm;
故答案为:C.
分析:分两种情况:如图(1),线段AB与水平方向垂直;如图(2),线段AB与水平方向不垂直,分别进行讨论即可得出答案.
6.D
考点:平行线之间的距离
解:设EF=GH=PQ=MN=x,
由面积公式得:两条道路的占地面积分别是AB?x和AB?x,
即两条道路的占地面积情况是相等,
故选D.
分析:根据平行线之间的距离和面积公式求出即可.
7.B
考点:平行线之间的距离
解:∵AB∥DC,
∴△ABC与△ABD的面积相等,
∵AE∥BD,
∴△BED与△ABD的面积相等,
∵ED∥BC找不到与△ABD等底等高的三角形,
∴和△ABD的面积相等的三角形有△ABC、△BDE,共2个.
故选B.
分析:根据两平行直线之间的距离相等,再根据等底等高的三角形的面积相等,找出与△ABD等底等高的三角形即可.
8.
D
考点:平行线之间的距离
解:如图,
当点A、B、P共线,且AB⊥a时,直线a、b之间的最短,所以直线a、b之间的距离≤PA+PB=3+4=7.
即直线a、b之间的距离不大于7.
故选:D.
分析:当点A、B、P共线,且AB⊥a时,直线a、b之间的距离为PA+PB.
9.
A
考点:平行线之间的距离
解:∵四边形ABCD中,AD∥BC,AC与BD相交于点O,S△ABD=10cm2
,
∴△ABD和△ACD如果都以AD做底边时,此时底边上的高相等,
∴S△ACD=10cm2
,
故选A.
分析:根据题意可知△ABD和△ACD如果都以AD做底边时,此时底边上的高相等,从而可以得到S△ACD的值.
10.
A
考点:平行线之间的距离,三角形的面积
解:过点A作AE⊥BC,垂足为E,过点D作DF⊥BC,垂足为F,如下图所示
由题意得:
,
∵AD∥BC
∴AE=DF
∴S1=S2
故答案为:A.
分析:本题不难发现两个三角形的底都是BC,要比较两个三角形的面积,就是比较高的大小,把两个三角形的高画出来,再根据平行,即可得到高相等,所以两个三角形的面积相等.
二、填空题
11.公垂
考点:平行线之间的距离
解:两条平行线间的所有公垂线段都相等,
故答案为:公垂.
分析:根据“在两条平行线之间的线段中,垂直两条平行线的线段最短,这条线段的长叫做平行线之间的距离”可知:在两条平行线之间再画几条和平行线垂直的线段,这些线段的长度都相等;据此判断即可.
12.
BP
考点:平行线之间的距离
解:由图可得,a∥b,BP⊥a,
∴直线a与直线b之间的距离是线段BP的长度,
故答案为:BP.
分析:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,由此可得出答案.
13.
5
考点:平行线之间的距离
解:AD与BC间的距离就是CE的长度,
?
∴AD与BC间的距离是5,
故答案为:5.
分析:AD与BC间的距离就是CE的长度,从而可得出答案.
14.
考点:平行线之间的距离,三角形的面积
解:作AE⊥BC于E,
∵四边形ABCD是平行四边形,且∠BAD=150
,
∴∠ABC=180
150
=30
,
在Rt△ABE中,AB=8cm,∠AEB=90
,∠ABC=30
,
∴AE=
AB=4cm,
∵
(
)
.
故答案为:
20
.
分析:根据平行线之间的距离处处相等,求出BC和AE的长,再利用三角形的面积计算公式求解即可。
三、综合题
15.
(1)解:∵AC⊥a,BD⊥a,
∴AC∥BD
(2)解:∵a∥b,AC⊥a,BD⊥a,
∴AC=BD
考点:平行线之间的距离
分析:(1)根据平行线的判定定理即可得出结论;(2)根据平行线间的距离即可得出结论.
16.
(1)证明:如图1,
连接AC,
∵AD∥BC,∴∠DAC=∠BCA
∵AB∥CD.∴∠BAC=∠DCA
在△ABC和△CDA中,
,
∴△ABC≌△CDA(ASA),
∴AB=CD
(2)证明:如图2,
作DE∥AB交BC于点E,
∵AD∥BC,
∴AB=DE
∵AB=CD,
∴DE=CD,
∴∠DEC=∠C
∵DE∥AB,
∴∠B=∠DEC,
∴∠B=∠C
(3)解:如图3,
作DF∥AC交BC的延长线于点F
∵AD∥BC,∴AC=DF、AD=CF,
∵DF∥AC,∴∠BDF=∠BEC,
∵AC⊥BD,∴∠BDF=∠BEC=90°,
在Rt△BDF中,由勾股定理得:BF=5,
故BC+AD=BC+CF=BF=5.
考点:平行线之间的距离,全等三角形的判定与性质
分析:探索:利用平行线的性质得出,∠DAC=∠BCA,∠BAC=∠DCA,进而得出△ABC≌△CDA(ASA),求出即可;应用一:作DE∥AB交BC于点E,利用平行线的性质得出∠B=∠C;应用二:利用平行线的性质结合勾股定理得出AD与BC两条线段的和.
17.
(1)解:当BF<BC时,∠BAF<∠BAC,
∴
<6,
解得t<
,
当0<t<
时,∠BAF<∠BAC
(2)解:分两种情况讨论:
????
点F在点C左侧时,AE=CF,
则2(t+1)=6﹣
t,
解得t=
;
②当点F在点C的右侧时,AE=CF,
则2(t+1)=
t﹣6,
解得t=
,
综上所述,t=
,t=
时,AE=CF
(3)解:当BF+AE<BC,S△ABF+S△ACE<S△ABC
,
t+2(t+1)<6,
解得t<
,
当0<t<
时,S△ABF+S△ACE<S△ABC
考点:平行线之间的距离,三角形的面积
分析:(1)根据边越长,边所对的角越大,可得答案;(2)分类讨论:当点F在点C左侧时,点F再点C的右侧时,可得关于t的一元一次方程,根据解方程,可得答案;(3)根据平行线间的距离相等,可得三角形的高相等,根据等高的三角形的底边越长,三角形的面积越大,可得不等式.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
