2020-2021学年浙教版八下数学拓展练习附答案第2章一元二次方程(word版含解析)
文档属性
| 名称 | 2020-2021学年浙教版八下数学拓展练习附答案第2章一元二次方程(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-21 18:37:59 | ||
图片预览


文档简介
浙教版八下数学第2章一元二次方程
一、选择题
下列方程是一元二次方程的是
A.
B.
C.
D.
已知关于
的一元二次方程
的一个根是
,则另一个根是
A.
B.
C.
D.
用配方法解一元二次方程
,配方正确的是
A.
B.
C.
D.
已知等腰三角形的两边长分别是一元二次方程
的两根,则该等腰三角形的底边长为
A.
B.
C.
D.
或
若关于
的一元二次方程
有两个实数根,则实数
的取值范围是
A.
B.
C.
且
D.
且
如图,在
中,,,.以点
为圆心,
的长为半径画弧,交线段
于点
,以点
为圆心,
长为半径画弧,交线段
于点
,则下列线段的长度是方程
的一个根的是
A.线段
的长
B.线段
的长
C.线段
的长
D.线段
的长
若
,则
的最小值是
A.
B.
C.
D.没有最小值
二、填空题
若关于
的方程
是一元二次方程,则
.
若
是方程
的根,则式子
的值为
.
在实数范围内定义运算“”:,则方程
的解为
.
设方程
的两根为
,,若
,则
.
若
,则
.
三、解答题
解下列方程:
(1)
;
(2)
.
已知关于
的一元二次方程
有两个实数根
,.
(1)
求实数
的取值范围;
(2)
当实数
为何值时,代数式
取得最小值?并求出该最小值.
已知关于
的方程
(
为常数).
(1)
该方程一定是一元二次方程吗?如果一定是,请说明理由;如果不一定是,请求出当方程不是一元二次方程时
的值;
(2)
求
时方程的解;
(3)
求出一个
的值,使这个
的值代人原方程后,所得的方程中有一个解与()中方程的一个解相同.(本小题只需求一个
的值即可)
一个两位数,十位数字与个位数字的和为
,把这个两位数的个位数字与十位数字对调后,所得的新两位数与原来的两位数的乘积为
,求原来的两位数.
受新冠疫情影响,实体店受影响很大,小明爸爸的服装店里堆积了一批服装打算在网上销售,平均每天可销售
件,每件盈利
元.为减少库存,小明的爸爸决定采取适当的降价措施.经调查发现,每件服装每降价
元,平均每天可多销售
件.
(1)
每件服装降价多少元时,小明爸爸的服装店的日盈利可达到
元?
(2)
小明爸爸的服装店的日盈利能否达到
元?
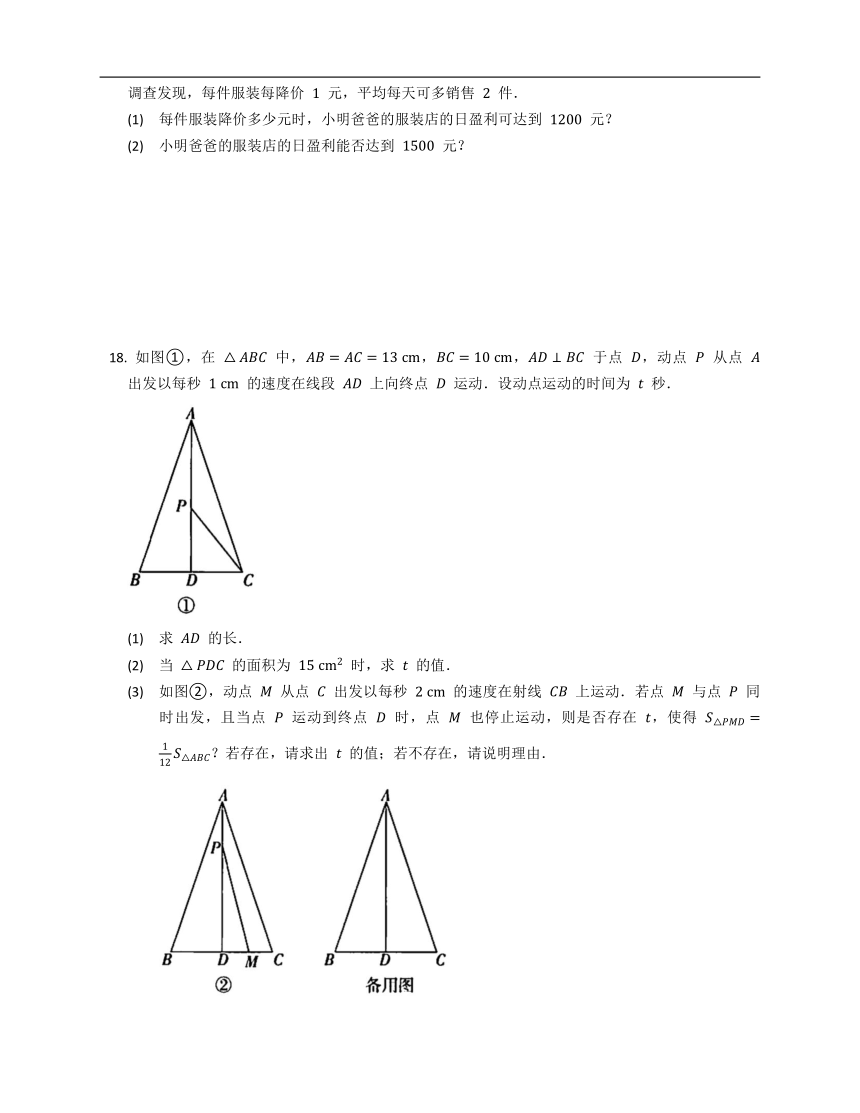
如图①,在
中,,,
于点
,动点
从点
出发以每秒
的速度在线段
上向终点
运动.设动点运动的时间为
秒.
(1)
求
的长.
(2)
当
的面积为
时,求
的值.
(3)
如图②,动点
从点
出发以每秒
的速度在射线
上运动.若点
与点
同时出发,且当点
运动到终点
时,点
也停止运动,则是否存在
,使得
?若存在,请求出
的值;若不存在,请说明理由.
答案
一、选择题
1.
【答案】B
【解析】A项中含有一个未知数,未知数的次数是
,不符合一元二次方程的定义;B项中是整式方程,且含有一个未知数,未知数的最高次数为
,符合一元二次方程的定义;C项中含有两个未知数,不符合一元二次方程的定义;D项中含有分式,不符合一元二次方程的定义.
2.
【答案】A
【解析】设另一个根为
,则
,解得
.
3.
【答案】A
【解析】移项,得
,
方程两边同除以
,得
,
方程两边都加上
,得
,
.
4.
【答案】A
【解析】
,,解得:
或
.
当等腰三角形的三边为
,,
时,不符合三角形三边关系定理,此时不能组成三角形;
当等腰三角形的三边为
,,
时,符合三角形三边关系定理,此时能组成三角形,此时三角形的底边长为
.
5.
【答案】C
【解析】根据题意,得
且
,
解得
且
.
6.
【答案】B
【解析】由勾股定理得
,
所以
,
解方程
得
,
即
,,
所以线段
的长是方程
的一个根.
7.
【答案】C
【解析】
,
,,
当
,
时,
有最小值,为
.
二、填空题
8.
【答案】
【解析】由一元二次方程的概念,得
解得
.
9.
【答案】
【解析】把
代入
,得
,
则
,
所以
.
10.
【答案】
【解析】由题意知
,即
,
,
,
.
11.
【答案】
【解析】
方程
的两根为
,,
由根与系数的关系得
,,
,
,
,
即
,
解得
,
当
时,判别式
,
都符合,
故答案为
.
12.
【答案】
【解析】将
变形,
得
,
设
,
则原方程变形为
,
解得
,,
或
,
又
,
.
三、解答题
13.
【答案】
(1)
所以所以
(2)
即所以所以
14.
【答案】
(1)
方程整理得
,
,
实数
的取值范围是任意实数.
(2)
根据题意得
,,
,
当
时代数式
取得最小值,该最小值为
.
15.
【答案】
(1)
不一定是一元二次方程.
当
时,该方程为一元一次方程,
解得
.
(2)
把
代入,得
,解得
,.
(3)
把
代入,得
.(或把
代人,得
)
16.
【答案】设原来的两位数十位上的数字为
,则个位上的数字为
,
依题意得
.
整理,得
,
解得
,.
当
时,;当
时,.
所以原来的两位数是
或
.
17.
【答案】
(1)
设降价
元,由题意得化简得解得答:每件服装降价
元或
元时,小明爸爸的服装店的日盈利可达到
元.
(2)
设降价
元,由题意得化简得,
方程
无实数根,
故小明爸爸的服装店的日盈利不能达到
元.
18.
【答案】
(1)
,,,
,且
,
,
.
(2)
当运动时间为
秒时,,,
的面积
,
,解得
.
(3)
假设存在
,使得
,
①当点
在线段
上,
即
时,
,,
由
,
得
,
整理得
,
解得
(舍去),.
②当点
在射线
上,即
时,,
由
,
得
,
整理得
,
解得
,.
综上,
的值为
或
或
时,使得
.
一、选择题
下列方程是一元二次方程的是
A.
B.
C.
D.
已知关于
的一元二次方程
的一个根是
,则另一个根是
A.
B.
C.
D.
用配方法解一元二次方程
,配方正确的是
A.
B.
C.
D.
已知等腰三角形的两边长分别是一元二次方程
的两根,则该等腰三角形的底边长为
A.
B.
C.
D.
或
若关于
的一元二次方程
有两个实数根,则实数
的取值范围是
A.
B.
C.
且
D.
且
如图,在
中,,,.以点
为圆心,
的长为半径画弧,交线段
于点
,以点
为圆心,
长为半径画弧,交线段
于点
,则下列线段的长度是方程
的一个根的是
A.线段
的长
B.线段
的长
C.线段
的长
D.线段
的长
若
,则
的最小值是
A.
B.
C.
D.没有最小值
二、填空题
若关于
的方程
是一元二次方程,则
.
若
是方程
的根,则式子
的值为
.
在实数范围内定义运算“”:,则方程
的解为
.
设方程
的两根为
,,若
,则
.
若
,则
.
三、解答题
解下列方程:
(1)
;
(2)
.
已知关于
的一元二次方程
有两个实数根
,.
(1)
求实数
的取值范围;
(2)
当实数
为何值时,代数式
取得最小值?并求出该最小值.
已知关于
的方程
(
为常数).
(1)
该方程一定是一元二次方程吗?如果一定是,请说明理由;如果不一定是,请求出当方程不是一元二次方程时
的值;
(2)
求
时方程的解;
(3)
求出一个
的值,使这个
的值代人原方程后,所得的方程中有一个解与()中方程的一个解相同.(本小题只需求一个
的值即可)
一个两位数,十位数字与个位数字的和为
,把这个两位数的个位数字与十位数字对调后,所得的新两位数与原来的两位数的乘积为
,求原来的两位数.
受新冠疫情影响,实体店受影响很大,小明爸爸的服装店里堆积了一批服装打算在网上销售,平均每天可销售
件,每件盈利
元.为减少库存,小明的爸爸决定采取适当的降价措施.经调查发现,每件服装每降价
元,平均每天可多销售
件.
(1)
每件服装降价多少元时,小明爸爸的服装店的日盈利可达到
元?
(2)
小明爸爸的服装店的日盈利能否达到
元?
如图①,在
中,,,
于点
,动点
从点
出发以每秒
的速度在线段
上向终点
运动.设动点运动的时间为
秒.
(1)
求
的长.
(2)
当
的面积为
时,求
的值.
(3)
如图②,动点
从点
出发以每秒
的速度在射线
上运动.若点
与点
同时出发,且当点
运动到终点
时,点
也停止运动,则是否存在
,使得
?若存在,请求出
的值;若不存在,请说明理由.
答案
一、选择题
1.
【答案】B
【解析】A项中含有一个未知数,未知数的次数是
,不符合一元二次方程的定义;B项中是整式方程,且含有一个未知数,未知数的最高次数为
,符合一元二次方程的定义;C项中含有两个未知数,不符合一元二次方程的定义;D项中含有分式,不符合一元二次方程的定义.
2.
【答案】A
【解析】设另一个根为
,则
,解得
.
3.
【答案】A
【解析】移项,得
,
方程两边同除以
,得
,
方程两边都加上
,得
,
.
4.
【答案】A
【解析】
,,解得:
或
.
当等腰三角形的三边为
,,
时,不符合三角形三边关系定理,此时不能组成三角形;
当等腰三角形的三边为
,,
时,符合三角形三边关系定理,此时能组成三角形,此时三角形的底边长为
.
5.
【答案】C
【解析】根据题意,得
且
,
解得
且
.
6.
【答案】B
【解析】由勾股定理得
,
所以
,
解方程
得
,
即
,,
所以线段
的长是方程
的一个根.
7.
【答案】C
【解析】
,
,,
当
,
时,
有最小值,为
.
二、填空题
8.
【答案】
【解析】由一元二次方程的概念,得
解得
.
9.
【答案】
【解析】把
代入
,得
,
则
,
所以
.
10.
【答案】
【解析】由题意知
,即
,
,
,
.
11.
【答案】
【解析】
方程
的两根为
,,
由根与系数的关系得
,,
,
,
,
即
,
解得
,
当
时,判别式
,
都符合,
故答案为
.
12.
【答案】
【解析】将
变形,
得
,
设
,
则原方程变形为
,
解得
,,
或
,
又
,
.
三、解答题
13.
【答案】
(1)
所以所以
(2)
即所以所以
14.
【答案】
(1)
方程整理得
,
,
实数
的取值范围是任意实数.
(2)
根据题意得
,,
,
当
时代数式
取得最小值,该最小值为
.
15.
【答案】
(1)
不一定是一元二次方程.
当
时,该方程为一元一次方程,
解得
.
(2)
把
代入,得
,解得
,.
(3)
把
代入,得
.(或把
代人,得
)
16.
【答案】设原来的两位数十位上的数字为
,则个位上的数字为
,
依题意得
.
整理,得
,
解得
,.
当
时,;当
时,.
所以原来的两位数是
或
.
17.
【答案】
(1)
设降价
元,由题意得化简得解得答:每件服装降价
元或
元时,小明爸爸的服装店的日盈利可达到
元.
(2)
设降价
元,由题意得化简得,
方程
无实数根,
故小明爸爸的服装店的日盈利不能达到
元.
18.
【答案】
(1)
,,,
,且
,
,
.
(2)
当运动时间为
秒时,,,
的面积
,
,解得
.
(3)
假设存在
,使得
,
①当点
在线段
上,
即
时,
,,
由
,
得
,
整理得
,
解得
(舍去),.
②当点
在射线
上,即
时,,
由
,
得
,
整理得
,
解得
,.
综上,
的值为
或
或
时,使得
.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
