4.6 反证法同步练习（含解析）

初中数学浙教版八年级下册4.6 反证法 同步练习
一、单选题
1.对一个假命题举反例时，应使所举反例（??? ）
A.?满足命题的条件，并满足命题的结论??????????????????B.?满足命题的条件，但不满足命题的结论
C.?不满足命题的条件，但满足命题的结论???????????????D.?不满足命题的条件，也不满足命题的结论
2.用反证法证明命题“一个三角形中至多有一个角是直角”，应先假设这个三角形中（?? ）
A.?至少有两个角是直角???????????????????????????????????????????B.?没有直角
C.?至少有一个角是直角???????????????????????????????????????????D.?有一个角是钝角，一个角是直角
3.要说明命题“两个无理数的和是无理数”，可选择的反例是（?? ）
A.?2，﹣3??????????????????????????B.?2 ， 3??????????????????????????C.?2 ，﹣ 2??????????????????????????D.?2 ， 2
4.用反证法证明“四边形至少有一个角是钝角或直角”时，应先假设（?? ）
A.?四边形中每个角都是锐角????????????????????????????????????B.?四边形中每个角都是钝角或直角
C.?四边形中有三个角是锐角????????????????????????????????????D.?四边形中有三个角是钝角或直角
5.用反证法证明“在同一平面内，若 a⊥c ， b⊥c ，则 a//b ”时，应假设（?? ）
A.?a//c??????????????????????????????B.?b//c??????????????????????????????C.?a//c ， b//c??????????????????????????????D.?a 与 b 相交
6.如图，在7×7的方格纸中，每个小方格都是边长为1的小正方形，网格线的交点称格点，点A，点B是方格纸中的两个格点，找出格点C，使△ABC的面积为3，则满足条件的格点C的个数是(??? )
A.?4个???????????????????????????????????????B.?5个???????????????????????????????????????C.?6个???????????????????????????????????????D.?8个
7.用反正法证明命题“如图，如果 AB//CD ， AB//EF ，那么 CD//EF ”时，证明的第一个步骤是（??? ）
A.?假设 AB 不平行于 CD
B.?假设 CD 不平行于 EF
C.?假设 CD//EF
D.?假设 AB 不平行于 EF
8.用反证法证明“四边形中至少有一个角是钝角或直角”时，第一步应先假设命题不成立，则下列各备选项中，第一步假设正确的是(???? )
A.?假设四边形中没有一个角是钝角或直角???????????????B.?假设四边形中有一个角是钝角或直角
C.?假设四边形中每一个角均为钝角?????????????????????????D.?假设四边形中每一个角均为直角
9.已知： ΔABC 中， AB=AC ，求证： ∠B<90? ，下面写出可运用反证法证明这个命题的四个步骤：
①∴ ∠A+∠B+∠C>180? ，这与三角形内角和为180°矛盾；
②因此假设不成立.∴ ∠B<90? ；
③假设在 ΔABC 中， ∠B≥90? ；
④由 AB=AC ，得 ∠B=∠C≥90? ，即 ∠B+∠C≥180? .
这四个步骤正确的顺序应是（?? ）
A.?③④②①???????????????????????????B.?③④①②???????????????????????????C.?①②③④???????????????????????????D.?④③①②
10.用反证法证明命题“在一个三角形中，至少有一个内角小于或等于 60° ”的过程如下:
已知: △ABC ;
求证: △ABC 中至少有一个内角小于或等于 60° .
证明:假设 △ABC 中没有一个内角小于或等于 60° ，即 ∠A>60°,∠B>60°,∠C>60° ，则
∠A+∠B+∠C>60°+60°+60°=180° ，
这与“__________” 这个定理相矛盾，
所以 △ABC 中至少有一个内角小于或等于 60° .
在证明过程中，横线上应填入的句子是（? ）
A.?三角形内角和等于 180°
B.?三角形的一个外角等于与它不相邻的两个内角的和
C.?等边三角形的各角都相等，并且每个角都等于 60°
D.?等式的性质
二、填空题
11.用反证法证明命题“在直角三角形中，至少有一个锐角不大于 45°”时第一步先假设所求证的结论不成立，即问题表述为________.
12.试说明命题“任何数a的平方都是正数”是假命题，可以举的反例是a＝________.
13.用反证方法证明“在 △ABC 中， AB=AC ，则 ∠B 必为锐角”的第一步是假设________.
14.用反证法证明“如果lal>a，那么a<0．”是真命题时，第一步应先假设________?．
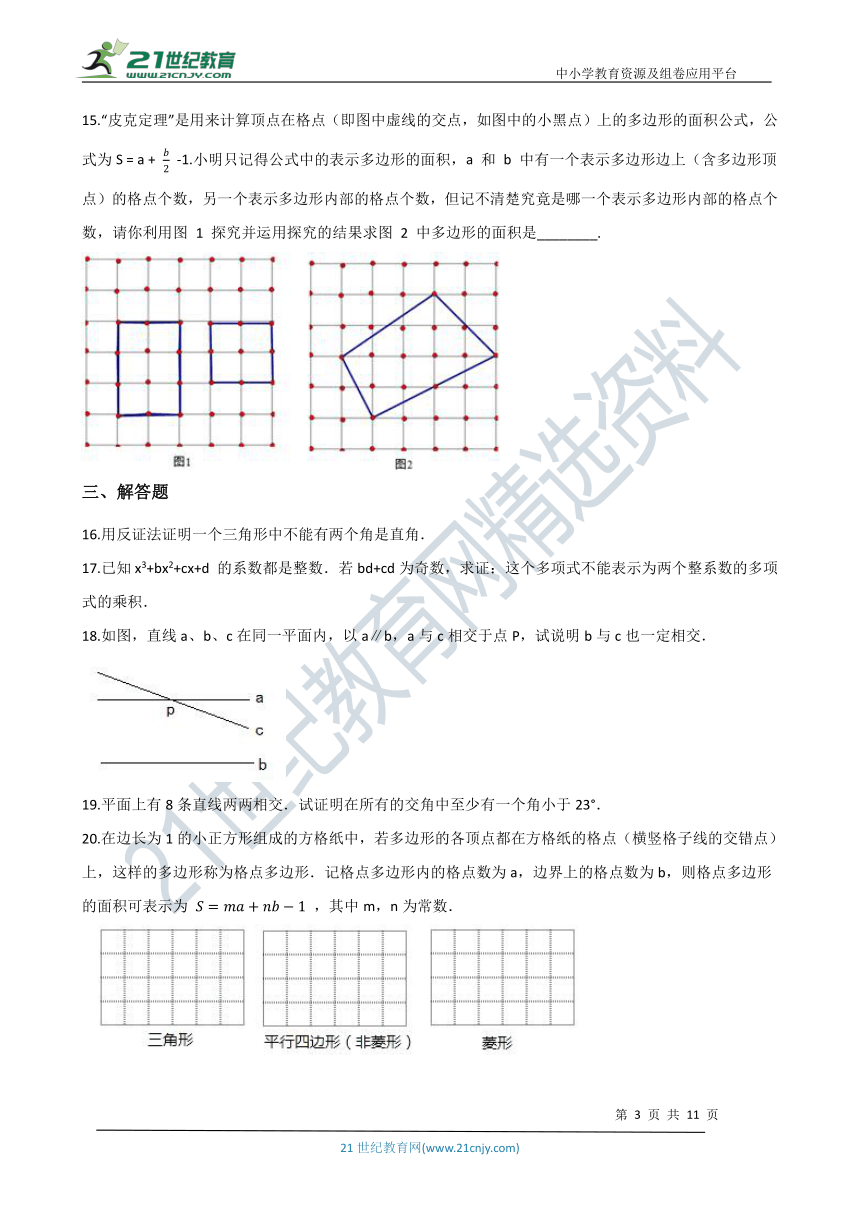
15.“皮克定理”是用来计算顶点在格点（即图中虚线的交点，如图中的小黑点）上的多边形的面积公式，公式为S = a + b2 -1.小明只记得公式中的表示多边形的面积，a 和 b 中有一个表示多边形边上（含多边形顶点）的格点个数，另一个表示多边形内部的格点个数，但记不清楚究竟是哪一个表示多边形内部的格点个数，请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是________.
三、解答题
16.用反证法证明一个三角形中不能有两个角是直角．
17.已知?x3+bx2+cx+d 的系数都是整数．若bd+cd为奇数，求证：这个多项式不能表示为两个整系数的多项式的乘积．
18.如图，直线a、b、c在同一平面内，以a∥b，a与c相交于点P，试说明b与c也一定相交．
19.平面上有8条直线两两相交．试证明在所有的交角中至少有一个角小于23°．
20.在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为 S=ma+nb-1 ，其中m，n为常数．
（Ⅰ）在下面的方格中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；
（Ⅱ）利用（Ⅰ）中的格点多边形确定m，n的值．
答案解析部分
一、单选题
1. B
考点：反证法
解：对一个假命题举反例时，应使所举反例满足命题的条件，但不满足命题的结论.
故答案为：B.
分析：假命题的判定只需举出一个反例，但反例要满足命题的条件，但不满足命题的结论.
2. A
考点：反证法
解：反证法是先提出一个与命题的结论相反的假设，所以先假设至少有两个角是直角.
故答案为：A．
分析：熟记反证法的步骤，然后进行判断．
3. C
考点：反证法
解：两个无理数的和是无理数是假命题，例如互为相反数的两个无理数和为0，0是有理数，
故答案为：C.
分析：反例就是满足命题的题设，但又不满足命题的结论的例子，根据互为相反数的两个数的和为0（而0是有理数）可判断求解.
4. A
考点：反证法
解：用反证法证明“四边形中至少有一个角是钝角或直角”时第一步应假设：四边形中每个角都是锐角.
故答案为：A.
分析：反证法的第一步就是假设结论的反面，由此可得答案。
5. D
考点：反证法
解：用反证法证明“在同一平面内，若 a⊥c ， b⊥c ，则 a//b ”时，应假设结论不成立
即假设 a 与 b 不平行，也即假设 a 与 b 相交
故答案为：D.
分析：根据反证法的一般步骤：先假设结论不成立即可得.
6. C
考点：三角形的面积
解：如图，

使△ABC的面积为3的点C有6个.
故答案为：C.
分析：分别在AB的两侧找到一个使△ABC的面积为3的点，再分别过这两个点作AB的平行线，即可得到满足格点C的个数。
7. B
考点：反证法
解：命题的结论为 CD//EF ，
∴反证法的第一步应为：假设CD不平行于EF．
故答案为：B．
分析：用反证法证明命题的第一步为从原命题结论的反面出发即可．
8. A
考点：反证法
解：用反证法证明“四边形中至少有一个角是钝角或直角”时第一步应假设：四边形中四个角都不是直角或钝角。
故答案为：A。
分析：此题考查了反证法，根据反证法的意义及步骤，在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须都否定。
9. B
考点：反证法
解：题目中“已知：△ABC中，AB=AC，求证：∠B＜90°”，用反证法证明这个命题过程中的四个推理步骤：
应该为：(1)假设∠B≥90°；(2)那么，由AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°；(3)所以∠A+∠B+∠C＞180°，这与三角形内角和定理相矛盾；(4)因此假设不成立.∴∠B＜90°。
原题正确顺序为：③④①②，
故答案为：B.
分析：根据反证法的证明步骤：①假设，②合情推理，③导出矛盾，④得出结论，据此进行排序即可.
10. A
考点：反证法
解：证明:假设 △ABC 中没有一个内角小于或等于 60° ，即 ∠A>60°,∠B>60°,∠C>60° ，则
∠A+∠B+∠C>60°+60°+60°=180° ，
这与“三角形内角和等于 180° ” 这个定理相矛盾，
所以 △ABC 中至少有一个内角小于或等于 60° .
故答案为：A
分析：根据反证法证明方法，先假设结论不成立，然后得到与定理矛盾，从而证得原结论成立.
二、填空题
11. 假设在直角三角形中，两个锐角都大于45°
考点：反证法
解：∵反证法的第一步是假设命题的结论不成立，∴用反证法证明命题“在直角三角形中，至少有一个锐角不大于 45°”时第一步即为，假设在直角三角形中，两个锐角都大于45°.
故答案为： 假设在直角三角形中，两个锐角都大于45°.
分析：反证法的第一步是假设命题的结论不成立，据此可以得出答案.
12. 0
考点：反证法
解：当a＝0时，02＝0，能说明命题“任何数a的平方都是正数”是假命题，
故答案为：0.
分析：举出符合已知条件但不满足结论的列子即可.
13. ∠B≥90°
考点：反证法
解：“ ∠B 必为锐角”的反面为 ∠B≥90°
故答案为：∠B≥90°.
分析：根据反证法的定义，找出结论的即可得出结论.
14. a≥0
考点：反证法
解： 如果a>a，那么a<0．”是真命题时?,用反证法证明第一步应假设a≥0.
故答案为：a≥0
分析：用反正法证明命题应先假设结论的反面成立，本题结论a<0的反面应是a≥0.
15. 10
考点：利用轴对称设计图案
解：根据图1可得，
∵矩形内由2个格点，边上有10个格点，面积为6，
即 6=2+102-1 ；
正方形内由1个格点，边上有8个格点，面积为4，
即 4=1+82-1 ；
∴公式中表示多边形内部整点个数的字母是 a ；
表示多边形边上（含多边形顶点）的格点个数为 b ，
由图 2 得： a=8,b=6,
∴S=a+b2-1=8+62-1=10.
故答案为：10
分析：分别找出图1中图形内的格点数和图形上的格点数后与公式比较即可发现表示图上的字母，再把图2中的相关数据代入计算即可求解.
三、解答题
16. 证明：
假设三角形的三个内角A、B、C中有两个直角，不妨设∠A=∠B=90°，
则A+B+C=90°+90°+C＞180°，这与三角形内角和为180°相矛盾，∴∠A=∠B=90°不成立；
所以一个三角形中不能有两个直角．
考点：反证法
分析：根据反证法的证法步骤知：第一步反设，假设三角形的三个内角A、B、C中有两个直角，不妨设∠A=∠B=90°，第二步得出矛盾：A+B+C=90°+90°+C＞180°，这与三角形内角和为180°相矛盾，∠A=∠B=90°不成立；第三步下结论：所以一个三角形中不能有两个直角，从而得出原命题正确．
17. 证明：假设该多项式能分解为两个整系数多项式的乘积，
∴x3+bx2+cx+d≡（x+a）（x2+mx+n）（a，m，n均是整数），
即x3+bx2+cx+d≡x3+（m+a）x2+（am+n）x+an，
∴b=m+a，c=am+n，d=an，
∵bd+cd=（b+c）d为奇数，
∴b+c是奇数且d也是奇数，
∴d=an可得a是奇数，n也是奇数，
∴b+c=m+a+am+n=m（a+1）+（a+n），
∴a+1是偶数，a+n也是偶数，
∴b+c也是偶数，这与题意相矛盾，
∴假设不成立，a，m，n不是整数，
∴这个多项式不能表示为两个整系数的多项式的乘积．
考点：反证法
分析：假设该多项式能分解为两个整系数多项式的乘积，即x3+bx2+cx+d≡（x+a）（x2+mx+n）≡x3+（m+a）x2+（am+n）x+an（a，m，n均是整数），根据恒等式相对应的系数相等，再分析，可得假设与题意相矛盾，即假设不成立，故得证.
18. 解：假设b与c不相交，那么b与c平行．
点P在直线a上，a与b平行，
所以P不在直线b上．
过直线b外的一点P，有两条直线a、c都与b平行．这与平行公理矛盾．
考点：反证法，平面中直线位置关系
分析：本题采用的方法叫做“反证法”．它是数学证明中的常用方法．采用反证法时，首先假设要证明的结论不成立，也就是相反的结论成立．再利用已知条件与假设导出矛盾，从而说明相反的结论不成立，原来的结论成立．
在判定两直线是否平行时，除了一般的判定定理外，我们还经常用到下面两条判定定理：(1)若两条直线同平行于第三条直线，则这两条直线平行．(2)若两条直线同垂直于第三条直线，则这两条直线平行．
19.证明：在平面上任取一点O，过O点分别作这8条直线的平行线l1'、l2'、l3'、l4'、l5'、l6'、l7' 、l8'；由平行线的性质知： l1'、l2'、l3'、l4'、l5'、l6'、l7' 、l8'之间互成的角与原来的8条直线 l1、l2、...、l8之间互成的角相等．
∴我们可考察l1'、l2'、l3'、l4'、l5'、l6'、l7' 、l8'与 l1' 所成的角，不难发现这8个角的和为一个平角，即180°．
假设这八个角没有一个小于23°，则这8个角的和至少为：23°×8=184°；这是不可能的．
∴这七个角中至少有一个小于23°，
不妨设为 l1' 与 l2' 的交角小于23°，
即原来的直线 l1与l2 所成的角小于23°．
考点：反证法
分析：假设这八个角没有一个小于23°，算出这8个角的和大于180°，与已知矛盾，从而得出原命题成立.
20.试题解析：（Ⅰ）如图所示：
? ；
（Ⅱ）∵格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为： S=ma+nb-1 ，其中m，n为常数，
∴三角形： S=3m+8n-1=6 ，平行四边形： S=3m+8n-1=6 ，菱形： S=5m+4n-1=6 ，则 {3m+8n-1=65m+4n-1=6 ，解得： {m=1n=12 ．
考点：作图-应用与设计作图．
考点：三角形的面积，平行四边形的性质
分析：试题分析：（Ⅰ）利用格点图形的定义结合三角形以及平行四边形面积求法画图即可；（Ⅱ）利用已知图形和 得出关于m，n的关系式，进而求解即可．